Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis
Подождите немного. Документ загружается.


4.2 Relations for partial quantities 65
Equation (4.6)isfrequently used for calculating chemical potentials as partial Gibbs
energies. For a binary 1–2 system one can regard G(T, P, x
1
, x
2
)asG(T, P, x
2
) because
x
1
+ x
2
= 1. This yields
µ
1
= G
1
= G
m
− x
2
dG
m
dx
2
(4.9)
µ
2
= G
2
= G
m
+ (1 − x
2
)
dG
m
dx
2
(4.10)
Exercise 4.1
For substitutional solutions one often defines an activity coefficient for a component i as
γ
i
= exp[(G
i
−
◦
G
i
− RT ln x
i
)/RT]. Show that for low contents of B and C in A one
has the following approximate relation under constant T and P,ifx
A
is not included in
the set of independent composition variables, ∂ ln γ
B
/∂x
C
= ∂ ln γ
C
/∂x
B
.
Hint
Start from a Maxwell relation ∂ G
B
/∂ N
C
= ∂
2
G/∂ N
C
∂ N
B
= ∂G
C
/∂ N
B
. Then go
from derivatives with respect to N
i
to derivatives with respect to x
i
by using x
i
=
N
i
/N; ∂x
i
/∂ N
i
= (N − N
i
)/N
2
= (1 − x
i
)/N; ∂x
i
/∂ N
j
=−N
i
/N
2
=−x
i
/N.
Solution
G
i
=
◦
G
i
+ RT ln x
i
+ RT ln γ
i
; ∂G
B
/∂ N
C
= RT[(1/x
B
)(−x
B
/N) + (∂ ln γ
B
/
∂ N
C
)] = ∂G
C
/∂ N
B
= RT[(1/x
C
)(−x
C
/N) + ∂ ln γ
C
/∂ N
B
] and thus ∂ ln γ
B
/∂ N
C
=
∂ ln γ
C
/∂ N
B
,exactly. However, we should examine derivatives with respect to x
i
and
not N
i
. Notice that we should choose an analytical expression for γ
B
containing x
B
and
x
C
as independent variables. For small x
B
and x
C
we get approximately
∂ ln γ
B
/∂ N
C
= (∂ ln γ
B
/∂x
B
)(−x
B
)/N + (∂ ln γ
B
/∂x
C
)(1 − x
C
)/N
∼
=
(∂ ln γ
B
/∂x
C
)/N
∂ ln γ
C
/∂ N
B
= (∂ ln γ
C
/∂x
B
)(1 − x
B
)/N + (∂ ln γ
C
/∂x
C
)(−x
C
)/N
∼
=
(∂ ln γ
C
/∂x
B
)/N.
Thus, ∂ ln γ
B
/∂x
C
∼
=
∂ ln γ
C
/∂x
B
.
4.2 Relations for partial quantities
In Section 3.2 we saw how an expression for the integral internal energy could be derived
by integration over a homogeneous system. It will now be demonstrated that the same
method can be applied to any other extensive quantity, A. Consider a homogeneous
system with constant T, P and x
i
. Then all the partial quantities A
i
are also constant.
We select an infinitely small subsystem and allow it to grow by simply extending its

66 Practical handling of multicomponent systems
imaginary wall. The growth in size may be represented by dN and the increase of the i
content is obtained as
dN
i
= x
i
dN. (4.11)
By integrating the differential of A under constant T and P and remembering that all A
i
and x
i
are constant, we obtain from the definition of A
i
, Eq. (4.2),
A =
dA =
A
i
dN
i
=
A
i
x
i
dN = A
i
x
i
dN
= A
i
x
i
N = A
i
N
i
(4.12)
A
m
≡ A/N = A
i
x
i
. (4.13)
It may again be emphasized that the partial quantities are always defined with T and P as
independent variables. If we were to define a corresponding quantity under constant T and
V, for instance, it would not have the same properties because V is an extensive variable.
By differentiating A = A
i
N
i
we obtain
dA = A
i
dN
i
+ N
i
dA
i
. (4.14)
Comparison with the expression for dA in Eq. (4.2), yields
N
i
dA
i
− (∂ A/∂T )
P,N
i
dT −(∂ A/∂ P)
T,N
i
dP = 0. (4.15)
This expression is most useful when applied to the Gibbs energy, giving
N
i
dG
i
+ SdT − V dP = 0. (4.16)
This is identical to the Gibbs–Duhem relation, Eq. (3.34), since G
i
is identical to µ
i
.
For other quantities it may be most useful under conditions of constant T and P.Asan
example, for volume we would obtain, under constant T and P,
N
i
dV
i
= 0orx
i
dV
i
= 0. (4.17)
Since all the partial quantities are defined as the partial derivatives with respect to some
content under constant T and P,itisevident that the following relations hold between
them
µ
j
= G
i
= H
i
− TS
i
= U
i
+ PV
i
− TS
i
= F
i
+ PV
i
. (4.18)
It is also evident that the expressions for other extensive state variables as derivatives
of the characteristic state functions can be applied to partial quantities as well. As an
example, we can start from an expression for S in terms of G and derive a similar
expression for S
j
in terms of G
j
,
S =−
∂G
∂T
P,N
i
(4.19)
S
j
=
∂ S
∂ N
j
T,P,N
l
=−
∂
∂ N
j
∂G
∂T
P,N
i
T,P,N
l
=−
∂
∂T
∂G
∂ N
j
T,P,N
i
P,N
l
=−
∂G
j
∂T
P,N
i
=−
∂µ
j
∂T
P,N
i
. (4.20)

4.3 Alternative variables for composition 67
Furthermore, from the Gibbs–Duhem relation, Eq. (3.34), we obtain by taking the deriva-
tive with respect to N
j
,
V
j
dP − S
j
dT = dµ
j
+
i
N
i
∂µ
i
∂ N
j
= dµ
j
+
i
N
i
∂
2
G
∂ N
i
∂ N
j
. (4.21)
It should be emphasized that the summation of terms cannot be omitted. As a conse-
quence, it is not possible to derive a Gibbs–Duhem relation for the partial quantities.
Finally, by applying Eqs (4.11) and (4.13)toEqs (1.11) and (1.38)wecan write the first
and second laws in the following forms
dU = dQ + dW +
H
i
dN
i
(4.22)
dS = dQ/T +
S
i
dN
i
+ d
ip
S. (4.23)
Exercise 4.2
Derive the relation H
j
= (∂(µ
j
/T )/∂(1/T ))
P,N
i
from H = (∂(G/T )/∂(1/ T ))
P,N
i
in Eq. (2.25).
Solution
H
j
= (∂ H/∂ N
j
)
T,P,N
k
= (∂(∂(G/T )/∂(1/T ))
P,N
i
/∂ N
j
)
T,P,N
k
= (∂(∂(G/T )/∂ N
j
)
T,P,N
k
/∂(1/T ))
P,N
i
= (∂(G
j
/T )/∂(1/T ))
P,N
i
= (∂(µ
j
/T )/∂(1/T ))
P,N
i
.
4.3 Alternative variables for composition
By composition we mean the relative amounts of various components, preferably the
set of molar contents, x
i
.Weshall now examine different ways of expressing the molar
contents in a ternary system. The same methods may be applied in higher-order systems.
In order to distinguish the methods we shall use a number of different notations.
(i) x
j
= N
j
/N = N
j
/N
i
(ii) z
j
= N
j
/N
1
= x
j
/x
1
(iii) u
j
= N
j
/(N
1
+ N
2
+···+N
k
) = N
j
/( N − N
k+1
−···) =x
j
/(1 − x
k+1
− ···).
The size of the system is thus measured by N, N
1
and (N
1
+ N
2
+···+N
k
), respec-
tively.
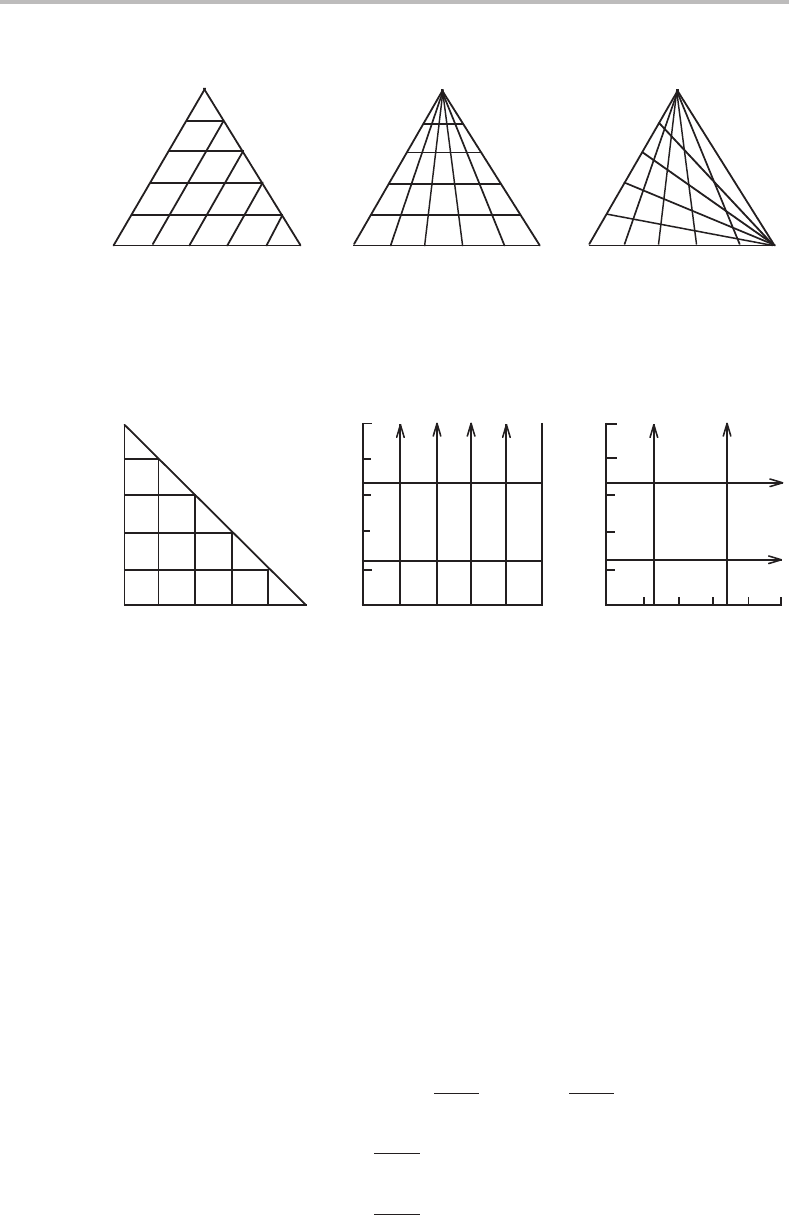
The characteristics of the three methods for a ternary system (with k = 2inthe third
method) are compared in Fig. 4.1,where the regular triangle introduced by Gibbs is
shown in Fig. 4.1(a). Isopleths (lines along which some composition variable is held
constant) according to the other schemes are shown in Fig. 4.1(b) and (c).Itshould be
noticed that the isopleths for u
2
are also isopleths for u
1
, since u
1
+ u
2
= 1. In Fig. 4.1(c)
it should be noticed that z
1
= 1everywhere. The three diagrams are redrawn with linear
scales for each kind of variable in Fig. 4.2. Here, the isopleths with arrows extend to
68 Practical handling of multicomponent systems
0.4
0.2
0
1.5
0.67
0.25
4.0
1.5
0.67
0.25
4.0
0.6
0.8
1.0(a) (b) (c)
∞
∞
∞
00
x
3
u
3
z
3
x
2
z
2
0 0.2 0.4 0.6 0.8 1
u
2
0.2 0.4 0.6 0.8 1 0.25 0.67 1.5 4.000
Figure 4.1 The Gibbs triangle showing three different methods of representing composition. The
corners represent pure component 1, 2 and 3, respectively.
0.4
0
0.67
0.6
0.8
0.2
0.4
0
0.6
0.8
0.2
0.25
0.4
0.6
0.8
0.2
0.25
0.67
0.670.25
0
x
2
u
2
z
2
x
3
(a) (b) (c)
u
3
z
3
10 0.6 0.80.2 0.4 10 0.6 0.80.2 0.4 10 0.6 0.80.2 0.4
Figure 4.2 The diagrams from Fig. 4.1 drawn with linear scales for the actual composition
variables. The arrows indicate that the component is situated at infinity and parallel lines with an
arrow pointing to the same pure component at infinity.
infinity. It should be emphasized that any line, which is straight in the Gibbs triangle, is
still a straight line in these modified diagrams.
When these new composition variables are used, the calculation of partial quantities is
changed. Before turning to these calculations, it should be realized that the definition of all
the molar quantities to be used in one context should be modified in the same way. Taking
the Gibbs energy as an example, its molar quantity should be defined as G/N
1
when dis-
cussed in connection with z
i
(case (ii)) and G/(N
1
+ N
2
)when discussed in connection
with u
i
(case(iii)) if k = 2. We shall denote these molar quantities by G
m1
and G
m12
.
With the method used in deriving an expression for A
j
in Section 4.1 we obtain, for
case (ii),
G = N
1
G
m1
(z
1
, z
2
, z
3
) with z
1
= 1 (4.24)
µ
1
≡ G
1
= G
m1
− z
2
∂G
m1
∂z
2
z
3
− z
3
∂G
m1
∂z
3
z
2
(4.25)
µ
2
≡ G
2
= z
2
∂G
m1
∂z
2
z
3
(4.26)
µ
3
≡ G
3
= z
3
∂G
m1
∂z
3
z
2
. (4.27)

4.3 Alternative variables for composition 69
For case (iii) we have
G = (N
1
+ N
2
)G
m12
(u
1
, u
2
, u
3
) with u
1
+ u
2
= 1 (4.28)
µ
1
≡ G
1
= G
m12
+
∂G
m12
∂u
1
u
l
−
u
i
∂G
m12
∂u
i
u
l
(4.29)
µ
2
≡ G
2
= G
m12
+
∂G
m12
∂u
2
u
l
−
u
i
∂G
m12
∂u
i
u
l
(4.30)
µ
3
≡ G
3
=
∂G
m12
∂u
3
u
l
. (4.31)
On the other hand, it should be emphasized that many equations derived with the ordinary
wayofexpressing the size of the system, will hold without further modification, if one
simply replaces all molar contents x by the corresponding z or u and all other molar
quantities by the corresponding molar quantities which may be denoted by A
m1
or A
m12
.
The following relations are useful
u
j
= N
j
/(N
1
+ N
2
) = x
j
/(x
1
+ x
2
) (4.32)
A
m12
= A/(N
1
+ N
2
) = A/N (x
1
+ x
2
) = A
m
/(x
1
+ x
2
) (4.33)
A
m12
= A/(N
1
+ N
2
) = N
i
A
i
/(N
1
+ N
2
) = u
i
A
i
(4.34)
z
j
= N
j
/N
1
= x
j
/x
1
(4.35)
A
m1
= A/N
1
= A/Nx
1
= A
m
/x
1
(4.36)
A
m1
= A/N
1
= N
i
A
i
/N
1
= z
i
A
i
= A
1
+ z
2
A
2
+ z
3
A
3
. (4.37)
It should be observed that A
i
is the usual partial quantity (∂ A/∂ N
i
)
T,P.N
j
.
Sometimes it may be convenient to use the notations A
m
and x
i
for all these quantities.
It is then necessary always to specify how one mole is defined, i.e. whether one considers
one mole of 1, one mole of 1 + 2orone mole total. In higher-order systems one may
measure the size of the system in several ways. It may be convenient to use the notations
u
i(1...k)
and A
m(1... k)
where 1...k are the components used to measure the size.
Exercise 4.3
Show that µ
2
= G
m
+ (1 − x
2
)(∂G
m
/∂x
2
)
x
3
/x
1
in a ternary system.
Hint
Replace variables N, N
2
and N
3
using x
2
(= N
2
/N), x
3
/x
1
(= N
3
/N
1
) and N(= N
1
+
N
2
+ N
3
).
Solution
Let G
m
be a function of x
2
and x
3
/x
1
: G = NG
m
(x
2
, x
3
/x
1
); µ
2
= (∂G/∂ N
2
)
N
1
,N
3
=
G
m
+ N (∂G
m
/∂x
2
)
x
3
/x
1
(∂x
2
/∂ N
2
)
N
1
,N
3
+ N (∂G
m
/∂(x
3
/x
1
))
x
2
(∂(x
3
/x
1
)/∂ N
2
)
N
1
,N
3
=
G
m
+ N (∂G
m
/∂x
2
)
x
3
/x
1
(N − N
2
)/N
2
+ N (∂G
m
/∂(x
3
/x
1
))
x
2
·0 = G
m
+ (1 − x
2
)(∂G
m
/
∂x
2
)
x
3
/x
1
.
70 Practical handling of multicomponent systems
α
β
1
x
i
av
x
i
av
x
i
α
x
i
β
−−
x
i
av
x
i
β
f
β
f
β
f
α
x
i
x
i
−
x
i
α
x
i
β
−
(a) (b)
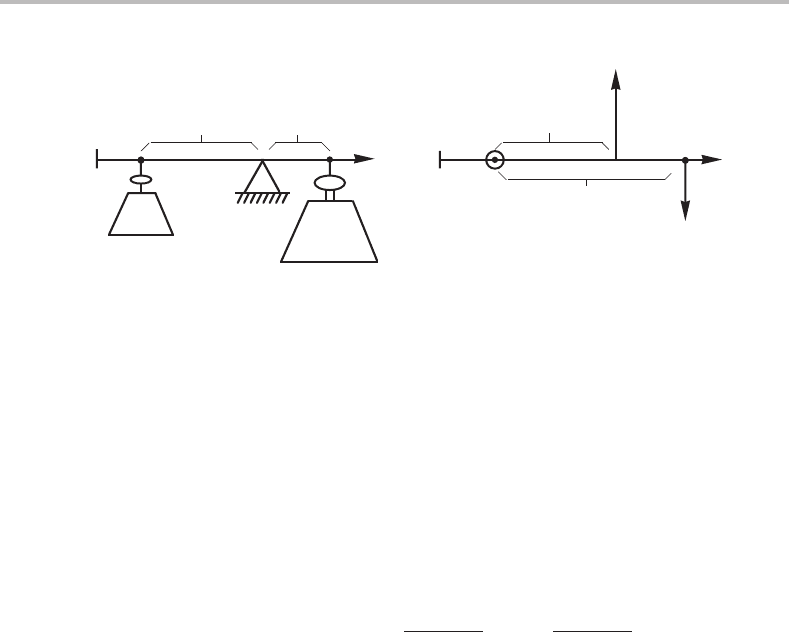
Figure 4.3 Twowaysofapplying the lever rule.
4.4 The lever rule
Let us consider some molar quantity A
m
in two homogeneous subsystems (phases), α
and β, with different properties, and then evaluate the average of the molar quantity, A
av
m
,
in the total system. By definition we have
A
α
m
= A
α
/N
α
(4.38)
A
β
m
= A
β
/N
β
. (4.39)
Using the law of additivity we obtain
A
av
m
≡ (A
α
+ A
β
)/(N
α
+ N
β
) = A
α
m
·
N
α
N
α
+ N
β
+ A
β
m
·
N
β
N
α
+ N
β
= f
α
A
α
n
+ f
β
A
β
n
.
(4.40)
The fractions of atoms present in each subsystem, i.e. the relative sizes of the two sub-
systems, are denoted by f
α
and f
β
. The terms can be rearranged because f
α
+ f
β
= 1.
f
α
A
av
m
− A
α
m
= f
β
A
β
m
− A
av
m
. (4.41)
This is often called the lever rule and is often used when A
m
is a molar content x
i
. That
case is illustrated in Fig. 4.3(a).
The terms can be rearranged in another way
A
av
m
− A
α
m
= f
β
A
β
m
− A
α
m
. (4.42)
This equation can be illustrated by two balancing forces, each of which tries to turn the
lever around the point representing the α subsystem (see Fig. 4.3(b)).
The lever rule can be extended to more subsystems. It is easy to see that
A
av
m
= f
α
A
α
n
+ f
β
A
β
n
+ f
γ
A
γ
n
+···. (4.43)
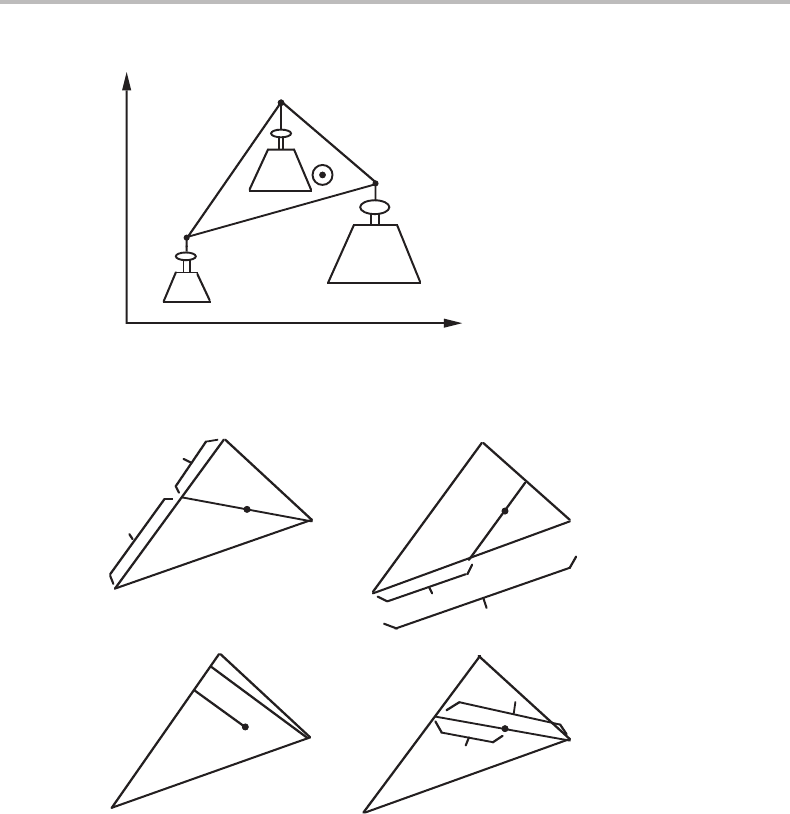
For three subsystems in a diagram with two molar quantities one obtains a triangle and
the total system will be represented by a point placed at its centre of gravity. This case
is illustrated in Fig. 4.4.
When the positions of the three subsystems and the total system are known, then one
can evaluate the fractions by several graphical methods, as illustrated in Fig. 4.5.
4.5 The tie-line rule 71
f
α
f
γ
f
β
α
β
γ
A
m
j
A
m
i
Figure 4.4 The lever rule applied to a system with three subsystems α, β and γ. The triangle is
regarded as capable of rotating around the point representing the whole system.
α
β
γ
α
α
α
β
β
β
γ
γ
1
1
1
γ
f
α
f
γ
f
β
f
β
f
β
(a)
(c)
(d)
(b)
Figure 4.5 (a)–(d) Four methods of evaluating the fractions of a subsystem, f
β
,orthe ratio of
fractions of two subsystems, f
α
/ f
γ
.
4.5 The tie-line rule
It is evident from Fig. 4.4 that a mixture of only two subsystems will fall on the straight
line between them, which is called tie-line or conode. This we shall call the tie-line
rule.Itmust be realized that it holds only if the same measure of size is used for both
quantities. In most applications we shall use the total number of moles or moles of a
specific element. An example is shown in Fig. 4.6. Both V
m
and x
B
were defined by
dividing V or N
B
by N. The value of V
m
for the composition x
B
is an average between
the end-points of the tangent. They represent the partial molar volumes, V
A
and V
B
, for
the same composition.
V
m
(x
B
) = x
A
V
A
(x
B
) + x
B
V
B
(x
B
). (4.44)
72 Practical handling of multicomponent systems
V
m
V
m
(x ′
B
)
V
A
(x ′
B
)
x ′
B
x ′
B
x ′
A
= 1−x ′
B
x
B
o
V
A
AB
dV
m
dx ′
B
V
B
(x ′
B
)
o
V
B
(1−x ′
B
)
Figure 4.6 Property diagram for a binary system showing the molar volume as a function of
composition at constant T and P. The intercepts made by the tangent give the partial quantities.
20
(a) (b)
0
01.0
o
G
A
G
A
(x ′
B
)
o
G
B
G
B
(x ′
B
)
G
m
(x ′
B
)
x ′
B
x
B
G
m
(kJ/mol)
40
30
20
0
0 2.0
slope =G
B
(z
B
)
z
B
=N
B
/N
A
z ′
B
o
G
A
G
A
(z ′
B
)
G/N
A
(kJ/mol)
Figure 4.7 Property diagram for a binary system showing the molar Gibbs energy as a function
of composition at constant T and P, using the total content of atoms, N,asameasure of size (a)
or N
A
(b).
The fact that the end-points of the tangent give the partial quantities can be shown with
Eq. (4.6). If x
B
is regarded as the only variable by treating x
A
as 1 − x
B
,weobtain
V
B
= V
m
+
dV
m
dx
B
− x
B
dV
m
dx
B
= V
m
+ (1 − x
B
)
dV
m
dx
B
. (4.45)
Two methods of measuring the size are compared in Figs. 4.7(a)and 4.7(b). The tie-
line rule applies to both. The rule does not apply to Fig. 4.8 because different measures
of size have there been used for the Cr and C contents. The straight lines in (a) have no
physical meaning but the curved lines in (b) are the true tie-lines. Other examples of
inconvenient choices will be given in Section 10.7.
The tie-line rule also holds in three dimensions. As an example, Fig. 4.9 shows a
molar Gibbs energy diagram for a ternary system and the intercepts of the tangent plane
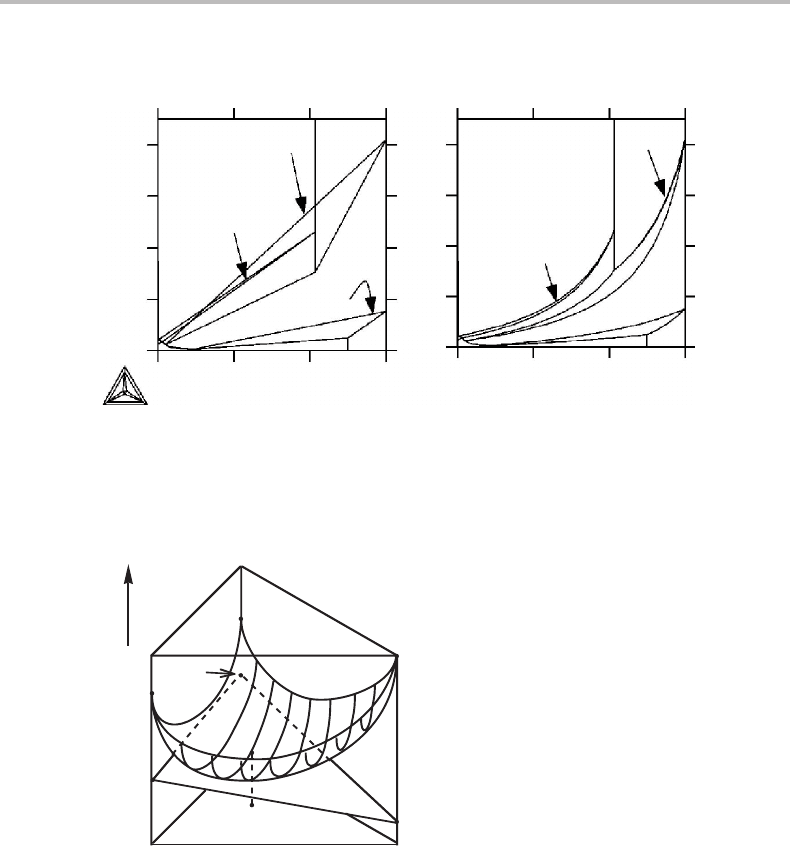
4.5 The tie-line rule 73
(b)(a)
γ+M
23
C
6
+M
7
C
3
γ+M
23
C
6
+M
7
C
3
γ+cem+M
7
C
3
γ+cem+M
7
C
3
α+γ+M
23
C
6
α+γ+M
23
C
6
Cr content as N
Cr
/N
Fe
3
4
2
1
0
0 0.1
x
C
0.2 0.3
0 0.1
x
C
0.2 0.3
Figure 4.8 z
Cr
, x
C
diagram for Fe–Cr–C at 1 bar and 1200 K. (a) is drawn under the incorrect
assumption that the tie-line rule applies; (b) is correct.
A
B
C
G
m
o
G
A
o
G
C
o
G
B
G
C
G
B
G
A
Figure 4.9 Molar Gibbs energy diagram for a ternary solution.
on the component axes represent the partial Gibbs energies. According to the tie-line
rule, the molar Gibbs energy of the alloy falls on the plane through these points. This
is also in accordance with Eq. (3.18), G
m
= x
i
µ
i
,where µ
i
is identical to G
i
(see
Equation (4.13)).
Exercise 4.4
Suppose one has measured the lattice parameter a of face-centred cubic (fcc)-Fe as a
function of the carbon content. What composition variable should be most convenient
in a diagram showing the volume of the unit cell, a
3
?

74 Practical handling of multicomponent systems
Hint
It would be most convenient if the tie-line rule could be applied. Then one could, for
instance, see immediately if the volume of a system would be different when carbon is
distributed uniformly or non-uniformly. Use the fact that carbon dissolves interstitially
in fcc-Fe.
Solution
The unit cell contains a fixed number of Fe atoms and a variable number of C atoms.
The volume of the unit cell is thus proportional to V /N
Fe
, i.e. V
m
/x
Fe
. The composition
should thus be expressed as N
C
/N
Fe
, i.e. x
C
/x
Fe
.
4.6 Different sets of components
When considering a system open to exchange of matter with the surroundings in
Section 3.1,weintroduced the terms µ
i
dN
i
in the expression for dU. These terms
were subsequently carried over into the expression for dG and a chemical potential for
any component j can thus be defined as
µ
j
=
∂G
∂ N
j
T,P,N
l
,ξ
. (4.46)
The quantity N
j
represents the amount of component j. The quantities N
i
and N are
often measured as the number of atoms or groups of atoms, whether the corresponding
molecule exists or not. However, the set of independent components can be chosen in
different ways and it is self-evident that whatever choice is made it cannot be allowed to
affect the total value of dG = µ
i
dN
i
.Asaconsequence, there is a relation between the
chemical potentials defined for different sets of components. Let us compare two sets.
As the first set we shall take the elements i, j, k, etc., and as the second set we shall take
formula units denoted by d, e, f, etc. Let a
d
i
be the number of i atoms in a formula unit
of d.Itisinteresting to note that the set of a
d
i
values for a new component d defines its
position in the i, j, k compositional space. If the formula unit of d is defined for one mole
of atoms then a
d
i
is equal to the molar contents of the elements in the new component,
x
d
i
. Further, let N
d
be the total number of formula units of the new component d. The
total number of i atoms in the system is then obtained by a summation over all the new
components.
N
i
=
d
a
d
i
N
d
. (4.47)
We thus obtain
µ
i
dN
i
=
i
µ
i
d
a
d
i
dN
d
=
d
i
a
d
i
µ
i
dN
d
. (4.48)
