Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

2.4 Experimental conditions 35

On the other hand, one can control the change in two other state variables, U and H,by

controlling the heat ﬂow

dU = dQ − PdV (2.16)

dH = dU + d(PV) = dQ + V dP. (2.17)

For some isothermal processes dQ/dξ is independent of the extent of the process, e.g.

melting of a pure substance. It is then convenient to deﬁne ξ as the amount of melt formed,

expressed in moles, and the heat of reaction per mole under constant P is obtained as





∂ Q

∂ξ



T,P

dξ =



∂ Q

∂ξ



T,P

. (2.18)

Anegative value implies that the process gives off heat to the surroundings under isother-

mal conditions. Such processes are called exothermic. Processes absorbing heat from

the surroundings are called endothermic. Equations (2.16) and (2.17) show that the heat

of reaction may be regarded as the energy or enthalpy of reaction, depending on whether

V or P is kept constant. It should be noted that the deﬁnition of heat of reaction, which

is based on treating Q in the ﬁrst law as positive when the system receives heat from the

surroundings, results in the heat of reaction being negative when heat is ‘generated’ by

the reaction, i.e. given off. That is opposite to common sense but may be accepted for

the sake of consistency.

Of course, Q itself is not a state variable, because it does not concern the system itself

but its interaction with another system, usually the so-called surroundings. An important

experimental technique is to keep the system thermally insulated from the surroundings,

i.e. to make dQ = 0, which is called adiabatic conditions. Experimental conditions

under which various state variables are kept constant are often given special names,

constant P isobaric

constant V isochoric

constant T isothermal

constant P and T isobarothermal

constant H isenthalpic

constant S isentropic

constant U isoenergetic

constant composition isoplethal

constant potential equipotential

From the above equations for dU and dH,itisevident that an isenthalpic reaction

can be accomplished under a combination of isobaric and adiabatic conditions and an

isoenergetic reaction can be realized under a combination of isochoric and adiabatic

conditions.

Let us now turn to the internal variables, which we have represented by the general

symbol ξ .Atequilibrium ξ has reached a value where the driving force for its change,

D,iszero. If the conditions are changed very slowly by an action from the outside, ξ

may vary slowly but all the time be very close to its momentary equilibrium value. In

36 Manipulation of thermodynamic quantities

Section 1.8 we have already concluded that D is then very low and the internal entropy

production,

S = Ddξ/T, (2.19)

is very low. In the limit, one talks about a reversible reaction where d

S = 0. In view of

the relation

T dS = dQ + Ddξ, (2.20)

we see that a reversible reaction, D = 0, which is carried out under adiabatic conditions,

dQ = 0, is isentropic. By examining the combined law in the variables T and V we see

that a reversible reaction, which is carried out under isothermal and isochoric conditions,

takes place under constant F. If it is carried out under isothermal and isobaric conditions,

it takes place under constant G. It is usual to consider such conditions and they may be

called isobarothermal conditions.

The heat ﬂow into a system on heating is often studied experimentally under con-

ditions that may not approach reversible ones. The heat capacity is deﬁned as follows,

independent of the reversible or irreversible character of the process.

C = dQ/dT. (2.21)

For isochoric conditions



∂U

∂T



(2.22)

because dU is always equal to dQ − PdV according to the ﬁrst law. For isobaric condi-

tions we obtain



∂ H

∂T



(2.23)

because dH is always equal to dQ + V dP according to the ﬁrst law.

We have already seen that for heat capacity the result will be different if ξ is kept at a

constant value or is allowed to be adjusted to its equilibrium value which varies with T. In

many experiments with molecular species, their amounts are frozen-in at reasonably low

temperatures and ξ is thus kept constant. At higher temperatures, the amounts may be

adjusted by molecular reactions and ξ may thus be adjusted to its equilibrium value. When

discussing C

and C

it may sometimes be wise to specify the conditions regarding ξ .

Usually it is assumed that the ξ values for all possible internal processes are adjusted to

their equilibrium values but it is not unusual to consider some process as frozen-in.

Exercise 2.4

The isothermal compressibility κ

is deﬁned as −(∂ V/∂ P)

/V ,where the derivative is

evaluated under reversible, isothermal conditions, i.e. a very slow compression, D = 0.

Show a similar way of deﬁning the adiabatic compressibility.

2.5 Notation for partial derivatives 37

Hint

Suppose the adiabatic compression is so rapid that there can be no internal process, i.e.

dξ = 0.

Solution

The second law gives T dS = dQ + Ddξ and both terms are now zero. We thus have

dS = 0 and can deﬁne the adiabatic compressibility as −(∂V /∂ P)

/V . This is why this

quantity is usually denoted by κ

. Note that this is justiﬁed only if the compression is

much faster than all internal reactions, including heat conduction.

2.5 Notation for partial derivatives

Since there are many alternative sets of independent variables it is necessary to indicate

which variables are to be kept constant in the evaluation of a particular partial derivative.

In order to simplify the notation for characteristic state functions, we can omit this infor-

mation when we use the natural variables, i.e. the particular set of independent variables

characteristic of the state function under consideration. Since G is the characteristic state

function for T, P we could then write ∂ G/∂ T instead of (∂G/∂ T )

. Furthermore, we may

introduce a shorthand notation for these derivatives, say G

. Second-order derivatives

can be denoted by two subscripts and G

would thus mean



∂

∂T



∂G

∂ P





∂

∂ P



∂G

∂T



= G

. (2.24)

Full information must be given as soon as a set of variables, different from the natural

one, is used.

The shorthand notation can be used for frozen-in conditions, dξ = 0, and for equilib-

rium conditions where ξ is regarded as a dependent variable. When there is any doubt

as to what conditions are considered, such information should be given.

Exercise 2.5

How should H

be interpreted?

Hint

Study the combined law in the form dH = T dS + V dP − Ddξ.

Solution

The natural variables of H are S and P. Thus H

is an illegal notation because T is not

one of the natural variables of H. We conclude that H

should not be used.

38 Manipulation of thermodynamic quantities

2.6 Use of various derivatives

Of course, C

and C

can both be related to any one of the characteristic state functions

but in each case a certain choice gives a shorter derivation. C

is deﬁned with T and

P as independent variables and we should thus use G,which has T and P as its natural

variables. The fundamental equation G = G(T,P)givesS =−(∂G/∂T )

and thus

H(T, P) = G + TS = G − T (∂G/∂T )

= (∂[G/T ]/∂[1/T ])

(2.25)

= (∂ H/∂T )

=−T (∂

G/∂ T

)

= T (∂ S/∂T )

. (2.26)

For C

we should use F(T,V ) and, since S =−(∂ F/∂T )

,weﬁnd in an analogous way

= (∂U/∂T )

=−T (∂

F/∂T

)

= T (∂ S/∂T )

. (2.27)

However, we may wish to compare the two heat capacities and must then be prepared to

derive both from the same characteristic state function, say G. For C

we already have

an expression − TG

, and C

will now be derived from U through G as a function of

T and P.

U = G + TS− PV = G − TG

− PG

(2.28)

dU = (G

− G

− TG

− PG

)dT +(G

− TG

− G

− PG

)dP

=−(TG

+ PG

)dT −(TG

+ PG

)dP. (2.29)

However, in order to evaluate C

which is equal to (∂U/∂T )

we must know U as a

function of T and V instead of T and P. We need a relation between dV,dT and dP. Starting

with V = (∂ G/∂ P)

= G

we obtain

dV = G

dT + G

dP (2.30)

dP = dV /G

− G

dT /G

. (2.31)

This gives dP as a function of dV and dT which can be inserted in the above equation

dU =−(TG

+ PG

)dT −(TG

+ PG

)(dV/G

− G

dT /G

). (2.32)

Remembering that G

is identical to G

,wethus obtain

= (∂U/∂T )

=−TG

− PG

+ T (G

)

+ PG

= T (G

)

− TG

(2.33)

so that

= C

+ T (G

)

. (2.34)

Using the same method we can derive an expression for any quantity in terms of the

derivatives of G with respect to T and P.

2.6 Use of various derivatives 39

It should be pointed out that, by tradition, one instead relates various quantities in

terms of the following three quantities which are directly measurable.

Heat capacity at constant pressure C

= (∂ H/∂T )

=−TG

(2.35)

Thermal expansivity α = (∂ V /∂T )

/V = G

(2.36)

Isothermal compressibility κ

=−(∂ V/∂ P)

/V =−G

. (2.37)

These three quantities are thus closely related to the three second-order derivatives G

and G

. The two schemes of relating quantities can easily be translated into each

other. It is interesting to note that through experimental information on the three quantities

, α, and κ

one has information on all the second-order derivatives of G.

Together, they thus form a good basis for an evaluation of the fundamental equation

G(T, P).

Exercise 2.6

Derive an expression for C

for a substance with G = a + bT + cT ln T + dT

+ fTP+ gP

Hint

Use either one of the equations given for C

but remember ﬁrst to make sure that the

proper variables are used.

Solution

Let us use C

= T (∂ S/∂T )

but then we must evaluate S(T, V ) from G. First, we get

−S(T, P) = (∂ G/∂ T )

= b + c + c ln T +2dT + fP.

In order to replace P by V we need V = (∂G/∂ P)

= e + fT + 2gP,which

gives −S = b + c + c ln T + 2dT + f (V − e − fT)/2g; C

= T (∂ S/∂T )

−T (c/T +2d − f

/2g) =−c − T (2d − f

/2g).

Exercise 2.7

Show how one can calculate the heat absorption on reversible isothermal compression

from easily measured quantities.

Hint

Since T and P are most easily controlled experimentally, we should use these variables. In

Exercise 1.7 we obtained the result Q = T

− S

)which could be very convenient but

only if the properties of the substance have already been evaluated from the experimental

information

40 Manipulation of thermodynamic quantities

Solution

Under reversible, isothermal conditions: dQ = T dS = T (∂ S/∂ P)

dP =−T (∂

∂T ∂ P)dP =−T (∂V /∂ T )

dP =−TVαdP; Q =−T



V αdP,where α = (∂ V/

∂T )

/V .

2.7 Comparison between C

and C

Let us now examine the relation between C

and C

in more detail. It is usually given in

the following form

= C

(1 + γαT ), (2.38)

where γ is a dimensionless quantity called Gr¨uneisen’s constant. By comparison with

the relation between C

and C

given by Eq. (2.35)wecan express γ in terms of the

directly measurable quantities

γ =−(G

)

/αC

= V α/κ

, (2.39)

where κ

and C

are both positive and, with few exceptions, α is also positive and it

is never strongly negative. The γ quantity often has a value of about 2. Note that C

always larger than C

, independent of the sign of α, because γα is equal to V α

/κ

which is always positive.

The quantity γ can be expressed in many ways, some of which are given here without

proof

γ =

− G



∂ S

∂V



= V



∂ P

∂U



. (2.40)

In all these forms γ is proportional to V,which in turn varies with T if P is kept constant. It

is evident that one cannot discuss how γ for a particular substance varies with T without

specifying if P or V is kept constant. If C

(T )isevaluated from C

(T ) using values

of γ and α measured at 1 bar, then the resulting values hold for different volumes at

different temperatures. C

may be regarded either as a function of T, V or T, P and it is

evident that the functions C

(T , V

) and C

(T , P

) are different. A comparison of the

two functions, evaluated from C

(T , P

) for tungsten is given in Fig. 2.1.Itshould be

emphasized that all other quantities, such as α and κ

, can also be treated as functions

of either T , V or T, P.

Exercise 2.8

Express F

and F

in terms of G

and G

. Then show that the second and third

members of Eq. (2.40) actually are equal.

Hint

=−S = G

and V = G

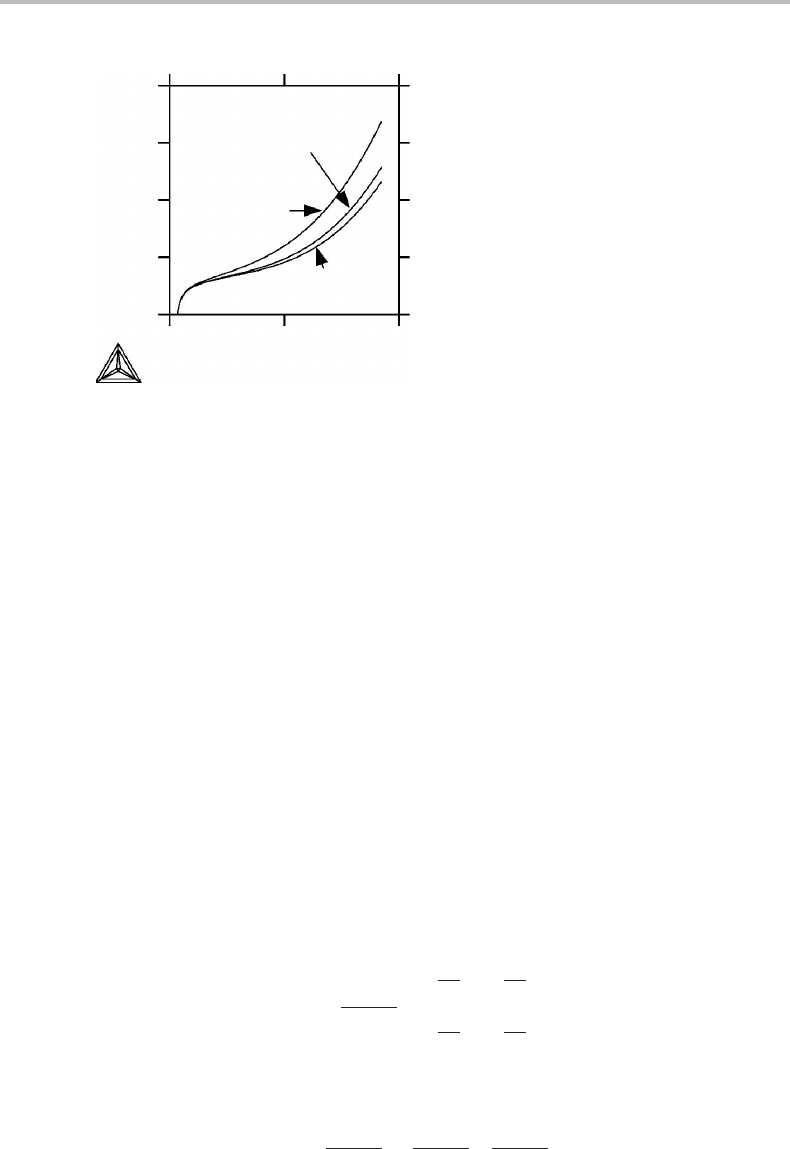
2.8 Change of independent variables 41

0 2000 4000

(T,P

)

(T,V

)

(T,P

)

C (J/molK)

T (K)

Figure 2.1 The heat capacity of tungsten evaluated in three different ways. Even though C

deﬁned as the heat capacity at constant V,itmay be regarded as a function of T, V or T, P.

At each temperature C

(T, P

)isevaluated at the volume given by the actual temperature

and a selected constant pressure P

Solution

In order to change from variables T and P to T and V,wecalculate from V = G

;

dV = G

dT + G

dP;dP = dV/G

− G

dV/G

From the hint: dF

= F

dT + F

dV = G

dT + G

dP = (G

− G

)dT + G

dV/G

Compare terms in these expressions: F

= G

− G

; F

= G

Third member: (VG

)/T (G

− G

) = G

/T (G

− G

which is the second member.

2.8 Change of independent variables

One often wants to change the set of independent variables. An example was given in

Section 2.6 where C

was ﬁrst given as (∂U/∂ T )

and was then evaluated as a function

of the derivatives of G with respect to T and P. Such changes can be made by the following

automatic procedure, which is based upon the properties of Jacobians. It is here given

without mathematical proof. We start by a deﬁnition of the Jacobian

∂(u, v)

∂(x, y)

≡



∂u

∂x

∂u

∂y

∂v

∂x

∂v

∂y



. (2.41)

It should be emphasized that the derivatives in the determinant are partial derivatives,

either under constant y or x.Itobeys the following rule

∂(u, v)

∂(x, y)

∂(u, v)

∂(r, s)



∂(x, y)

∂(r, s)

. (2.42)

We can thus introduce r and s as new independent variables instead of x and y.

42 Manipulation of thermodynamic quantities

The derivative of a thermodynamic quantity can be expressed by a Jacobian because

∂(u, y)

∂(x, y)



∂u

∂x

∂u

∂y

∂x

∂y



∂u

∂x

∂u

∂y





∂u

∂x



, (2.43)

and the new independent variables, r and s, can thus be introduced in the following way



∂u

∂x



∂(u, y)

∂(x, y)

∂(u, y)

∂(r, s)



∂(x, y)

∂(r, s)



∂u

∂r

∂u

∂s

∂y

∂r

∂y

∂s







∂x

∂r

∂x

∂s

∂y

∂r

∂y

∂s



(2.44)

It should be realized that ∂u/∂x actually means

(

∂u/∂ x

)

and ∂u/∂r means

(

∂u/∂r

)

This equation contains the following relations as special cases. They can of course be

proved in a much simpler way:



∂u

∂x



= 1



∂x

∂u



(2.45)



∂u

∂x



=−



∂y

∂x





∂y

∂u



. (2.46)

Exercise 2.9

Express

(

∂G/∂T

)

in terms of functions usually measured and tabulated.

Hint

Most measurements are made by controlling T and P. Change to these variables. Remem-

ber that ∂x/∂r and ∂ x/∂s in Eq. (2.44) mean (∂x/∂r )

and (∂x/∂s)

Solution

(∂G/∂T )



∂G/∂T ∂G/∂ P

∂V/∂ T ∂V/∂ P







∂T /∂ T ∂ T/∂ P

∂V/∂ T ∂ V/∂ P



= (∂ G/∂ T )

− (∂G/∂ P)

(∂V/∂ T )

/(∂V/∂ P)

=−S + V ακ

Exercise 2.10

A condensed phase is compressed adiabatically and reversibly from a pressure 0 to P.

Derive an equation for the temperature change in terms of easily measured quantities.

2.9 Maxwell relations 43

Hint

Adiabatic and reversible conditions are also isentropic. We want

(

∂T /∂ P

)

. Change the

variables to T and P.

Solution

(∂T /∂ P)



∂T /∂ T ∂T/∂ P

∂ S/∂ T ∂ S/∂ P







∂ P/∂T ∂ P/∂ P

∂ S/∂ T ∂ S/∂ P



=−(∂ S/∂ P)

/(∂ S/∂ T )

=−G

=−V α/(−C

/T ) = TVα/C

We thus get dT =

(

TVα/C

)

dP. The result does not depend on the compressibility

which may seem surprising. How could there be compression caused heating if the

phase is incompressible? The answer is that the thermal expansivity, α,iszero if the

compressibility is zero.

2.9 Maxwell relations

Some partial derivatives can be transformed in a very special way. The requirement is

that the variable to be kept constant is a conjugate variable to one of the numerators in

the derivative. The method may be illustrated by the following example:

dG =−SdT + V dP; −S =

(

∂G/∂T

)

; V =

(

∂G/∂ P

)

T (2.47)



∂V

∂T





∂(∂G/∂ P)

∂T



∂

∂ P∂ T

∂

∂T ∂ P



∂(∂G/∂T )

∂ P



=−



∂ S

∂ P



(2.48)

or by the shorthand notation



∂V

∂T



= G

=−



∂ S

∂ P



. (2.49)

The relations obtained in this way are called Maxwell relations. We can use any form of

the combined law and thus obtain a large number of such relations. It should be noticed

that all derivatives related by Maxwell relations are constructed in such a way that the

variable to be kept constant is conjugate to the quantity in the numerator but the relations

may be inverted, of course.

Exercise 2.11

Transform

(

∂V/∂ T

)

using a Maxwell relation.

44 Manipulation of thermodynamic quantities

Hint

Use the inverse quantity,

(

∂T /∂ V

)

in order to place the conjugate quantities, T and S,in

the right positions. Use the characteristic state function with V and S as natural variables,

i.e. U.

Solution

(∂V/∂ T )

= 1/(∂T /∂ V )

= 1/(∂

U/∂V ∂ S) =−1/(∂ P/∂ S)

=−(∂ S/∂ P)

Exercise 2.12

Prove the identity T (∂

P/∂T

)

= (∂C

/∂V )

Hint

Since T and V are the variables,it is convenient to base the solution on F and its derivatives.

dF =−SdT − PdV gives the following Maxwell relation:

(

∂ S/∂ V

)

(

∂ P/∂T

)

Also, use C

= T

(

∂ S/∂ V

)

from Eq. (2.27).

Solution

Using the Maxwell relation we get T (∂

P/∂T

)

= T (∂(∂ P/∂T )

/∂T )

= T (∂(∂ S/

∂V )

/∂T )

= T ∂

S/∂ V ∂T .From C

= T (∂ S/∂T )

we get (∂C

/∂V )

= T ∂

∂T ∂ V which is the same result.