Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

1.6 Second law of thermodynamics 15

this was done it was decided to express the difference between the boiling and freezing

point of water at 1 atm as 100 units, in agreement with the Celsius scale. This unit is

now called kelvin (K).

Let us now return to the irreversible process of heat conduction from a warm reservoir

to a cold one. By transferring an amount dQ one would decrease the entropy of the warm

reservoir by dQ/T

and increase the entropy of the cold one by dQ/T

. The net change

of the entropy would thus be

dS =−dQ/T

+ dQ/ T

= dQ · (T

− T

. (1.36)

This irreversible process thus produces entropy. One talks about internal entropy

production

S > 0. (1.37)

The subscript ‘ip’ indicates that this change of the entropy of the system is due to an

internal process. This is the second law of thermodynamics and it should be noted that it

concerns what happens inside a system, whereas the ﬁrst law concerns interactions with

the surroundings. As we have seen, the transfer of heat to the system, dQ, will increase

the entropy by dQ/T and, by also considering the effect of additional matter, dN,inan

open system we can write the second law as

dS = dQ/ T + S

dN + d

S > dQ/T + S

dN. (1.38)

is the molar entropy of the added material and can be derived exactly as H

in the

ﬁrst law was derived in Section 1.3.With the alternative deﬁnition of heat in Eq. (1.12)

we would obtain

dS = dQ

∗

/T − (H

/T − S

)dN + d

S = dQ

∗

/T − ((H

− TS

)/T )dN

S > dQ

∗

/T − ((H

− TS

)/T )dN. (1.39)

When a spontaneous process proceeds, it is in a direction that can be predicted from

the above criterion. A spontaneous process is always an irreversible process, other-

wise it would have no preferred direction and it would be reversible. A reversible pro-

cess is a hypothetical construction and can be deﬁned by either one of the following

criteria,

S = 0 (1.40)

dS = dQ/ T + S

dN. (1.41)

Exercise 1.6

Suppose a simple model for an internal reaction yields the following expression for

the internal production of entropy under conditions of constant T, V and N, 

S =

−ξ K /T − R[ξ ln ξ − (1 + ξ ) ln(1 + ξ )], where ξ is a measure of the progress of the

reaction going from 0 to 1. Find the equilibrium value of ξ, i.e. the value of ξ for which

the reaction cannot proceed spontaneously.

16 Basic concepts of thermodynamics

Hint

The spontaneous reaction will stop whend

S is no longer positive, i.e. whend

S/dξ = 0.

Solution

S /dξ = d(

S)/dξ =−K /T − R[1 + ln ξ − 1 − ln(1 + ξ )] = 0; ξ/(1 + ξ ) =

exp(−K /RT); ξ = 1/[exp(K/RT) − 1].

Exercise 1.7

Find a state function from which one could evaluate the heat ﬂow out of the system when

a homogeneous material is compressed isothermally.

Hint

Heat is not a state function of a system. In order to solve the problem we must know how

the change was made. Let us ﬁrst assume that it was reversible.

Solution

Forreversible conditions Q =



T dS = T



dS = T

− S

) and the heat extraction

−Q = T

− S

). For irreversible conditions dQ < T dS; Q < T

− S

) and the

extracted heat is −Q > T

− S

), i.e. larger than before. However, if the ﬁnal state

is the same, U must be the same because it is a state function and the higher value of

−Q must be compensated by a higher value of the work of compression W than during

reversible compression. How much higher −Q and W will be cannot be calculated without

detailed information on the factor making the compression irreversible.

Exercise 1.8

Consider a Carnot cycle with a non-ideal gas and suppose that the process is somewhat

irreversible. Use the second law to derive an expression for the efﬁciency.

Hint

For each complete cycle we have U = 0 and S = 0 because U and S are both

state functions.

Solution

U = W + Q

+ Q

= 0; S = Q

+ Q

+ 

S = 0where W and



S are the sums over the cycle. We seek η =−W/Q

and should thus eliminate

by combining these equations: −Q

= Q

+ 

S · T

; −W = Q

+ Q

−Q

− 

S · T

+ Q

= Q

− T

)/T

− 

S · T

and thus η =−W/Q

− T

)/T

− 

S · T

< (T

− T

)/T

because 

S, T

and Q

are all positive.

1.7 Condition of internal equilibrium 17

1.7 Condition of internal equilibrium

The second law states that an internal process may continue spontaneously as long as

S is positive. It must stop when for a continued process one would have

S ≤ 0. (1.42)

This is the condition for equilibrium in a system. By integrating d

S we may obtain a

measure of the total production of entropy by the process, 

S.Ithas its maximum

value at equilibrium. The maximum may be smooth, d

S = 0, or sharp, d

S < 0, but

the possibility of that alternative will usually be neglected.

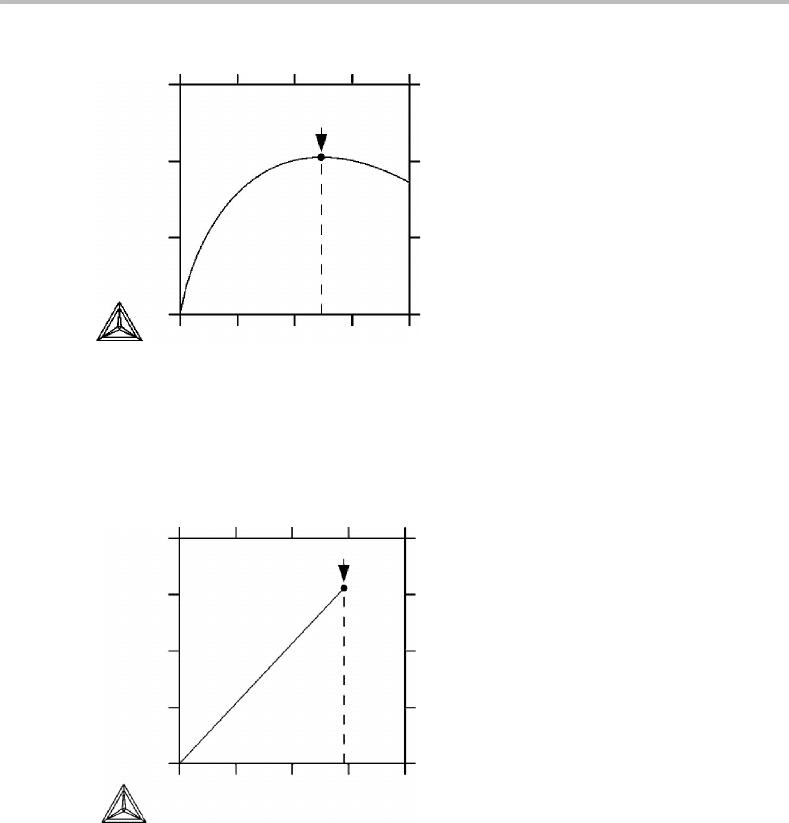
As an example of the ﬁrst case, Fig. 1.5 shows a diagram for the formation of vacancies

in a pure metal. The internal variable, generally denoted by ξ ,ishere the number of

vacancies per mole of the metal.

As an example of the second case, Fig. 1.6 shows a diagram for the solid state reaction

between two phases, graphite and Cr

0.7

0.3

,bywhich a new phase Cr

0.6

0.4

is formed.

The internal variable here represents the amount of Cr

0.6

0.4

. The curve only exists up

to a point of maximum where one or both of the reactants have been consumed (in

this case Cr

0.7

0.3

). From the point of maximum the reaction can only go in the reverse

direction and that would give d

S < 0which is not permitted for a spontaneous reaction.

The sharp point of maximum thus represents a state of equilibrium. This case is often

neglected and one usually treats equilibrium with the equality sign only, d

S = 0.

If d

S = 0itispossible that the system is in a state of minimum 

S instead of

maximum. By a small, ﬁnite change the system could then be brought into a state where

S > 0 for a continued change. Such a system is thus at an unstable equilibrium.As

a consequence, for a stable equilibrium we require that either d

S < 0, or d

S = 0but

then its second derivative must be negative.

It should be mentioned that instead of introducing the internal entropy production,

S, one has sometimes introduced dQ



/T where dQ



is called ‘uncompensated heat’.

It represents the extra heat, which must be added to the system if the same change of

the system were accomplished by a reversible process. Under the actual, irreversible

conditions one has dS = dQ/ T + d

S. Under the hypothetical, reversible conditions

one has dS = (dQ + dQ



)/T . Thus, dQ



= T d

S.Inthe actual process d

S is produced

without the system being compensated by such a heat ﬂow from the surroundings.

If the reversible process could be carried out and the system thus received the extra

heat dQ



,ascompared to the actual process, then the system must also have delivered

the corresponding amount of work to the surroundings in view of the ﬁrst law. Because

of the irreversible nature of the process, this work will not be delivered and that is why

one sometimes talks about the ‘loss of work’inthe actual process which is irreversible

and produces some entropy instead of work, dW = dQ



= T d

Exercise 1.9

Check the loss of work in a cyclic process working with a high-temperature heat source

of T

and a low-temperature heat sink of T

and having some internal entropy production.

18 Basic concepts of thermodynamics

1.5

1.0

0.5

5 10 15 20

ξ (fraction of vacancies, u

⋅10

)

on of vacancies, u

⋅10

)

(∆

S/R)⋅10

equilibrium

value of ξ

Figure 1.5 The internal entropy production due to the formation of thermal vacancies in 1 mole

of a pure element at a temperature where the energy of formation of a vacancy is 9kT, k being

the Boltzmann constant. The initial state is a pure element without any vacancies. The internal

variable is here the number of vacancies expressed as moles of vacancies per mole of metal, u

0.4

0.3

0.2

0.2 0.4 0.6 0.8

0.1

∆

S/R

equilibrium

value of ξ

ξ (moles of Cr

0.6

0.4

)

Figure 1.6 The internal entropy production due to the solid state phase transformation

C +Cr

0.7

0.3

→ Cr

0.6

0.4

at 1500 K and 1 bar. The initial state is 0.5 mole each of C(graphite)

and Cr

0.7

0.3

. The internal variable here represents the amount of Cr

0.6

0.4

Hint

In Exercise 1.8 we found −W = Q

− T

)/T

− 

S · T

a·

From this result we can

calculate the ‘loss of work’, e.g. if the amount of heat extracted from the heat source is

the same in the irreversible case as in the reversible one. Give this loss per heat extracted

from the heat source, and give it per heat given to the colder heat sink, Q

Solution

Forareversible cycle one would have −W = Q

− T

)/T

. The ‘loss of work’ per

extracted heat is thus 

S · T

1.8 Driving force 19

For the second case we should eliminate Q

from the two equations in the solu-

tion of Exercise 1.8: −Q

= 

S · T

+ Q

; −W = Q

+ Q

=−Q

− T

− 

S · T

The ‘loss of work’ per received heat is thus 

S · T

/(−Q

). The two results are

equal in the reversible limit where Q

=−Q

according to Eq. (1.35).

1.8 Driving force

Let the internal variable ξ represent the extent of a certain internal process. The internal

entropy production can then be regarded as a function of this variable and we may deﬁne

its derivative d

S/dξ as a new state variable. It may also be regarded as a state function

because it may be expressed as a function of a set of state variables, including ξ,which

deﬁne the state. For convenience, we shall multiply by T under isothermal conditions to

obtain a new state variable,

D ≡ T

dξ

. (1.43)

One may use D = 0asthe condition of equilibrium. This quantity was introduced by

De Donder [2]when considering chemical reactions between molecules and it was thus

called afﬁnity.However, it has a much wider applicability and will here be regarded as

the driving force for any internal process. The symbol D, chosen here, may either be

regarded as an abbreviation of driving force or as an honour to De Donder. It is usually

convenient to deﬁne ξ byavariable that is an extensive property, subject to the law of

additivity. The driving force D will then be an intensive variable.

If a system is not in a state of equilibrium, there may be a spontaneous internal process

for which the second law gives d

S > 0 and thus

T d

S = Ddξ>0. (1.44)

It is evident that dξ and D must have the same sign in order for the process to proceed. By

convention, dξ is given a positive value in the direction one wants to examine and D must

then be positive for a spontaneous process in that direction. In many applications one

even attempts to predict the rate of a process from the magnitude of D. Simple models

often predict proportionality. This will be further discussed in Chapter 5.

If D > 0 for some internal process, then the system is not in a state of equilibrium. The

process may proceed and it will eventually approach a state of equilibrium where D = 0.

The equilibrium value of the variable ξ can, in principle, be evaluated from the condition

D = 0, which is usually more directly applicable than the basic condition d

S = 0.

In the preceding section we connected an internal entropy production with the progress

of an internal process. However, we can now see that it is possible, in principle, to change

an internal variable without any entropy production. This can be done by changing the

external variables in such a way that the driving force D is always zero. Since D is zero at

equilibrium only, it is necessary to change the external variables so slowly that ξ can all

the time adjust itself to the new value required by equilibrium. In practice, this cannot be

20 Basic concepts of thermodynamics

completely achieved because the rate of the process should be zero if its driving force is

zero. An inﬁnitely slow change is thus necessary. Such an idealized change is identical to

the reversible process mentioned in the preceding section and it is sometimes described

as an ‘equilibrium reaction’. It would take the system through a series of equilibrium

states.

It may be convenient to consider a reversible process if one knows a state of equilibrium

for a system and wants to ﬁnd other states of equilibrium under some different conditions.

This is the reason why one often applies ‘reversible conditions’. As an example we may

consider the heating of a system under constant volume, discussed in Section 1.4. The

heat capacity under such conditions, C

,was found to be different under slow and rapid

changes. Both of these cases may be regarded as reversible because the internal entropy

production is negligible when D is small for a very slow change and also when dξ is

small for a frozen-in internal process. For both cases we may thus use dS = dQ/ T and

we obtain two different quantities,

≡



∂ Q

∂T



= T



∂ S

∂T



(1.45)

V,ξ

≡



∂ Q

∂T



V,ξ

= T



∂ S

∂T



V,ξ

. (1.46)

These expressions are equivalent to those given in Section 1.4 in terms of U.For inter-

mediate cases, which are not reversible, one should consider U and not S, i.e. use the

ﬁrst law and not the second law.

Exercise 1.10

Consider an internal reaction which gives an entropy production under isothermal condi-

tions, 

S =−ξ K /T − R[ξ ln ξ − (1 + ξ ) ln(1 + ξ )]. Derive the stability at equilib-

rium, deﬁned as B =−T ·d

S/dξ

=−T · dD/dξ. (See Section 6.1.)

Hint

In Exercise 1.6 we have already calculated d

S/dξ and ξ at equilibrium.

Solution

S/dξ =−K /T − R[ln ξ − ln(1 + ξ )]; d

S/dξ

=−R

[

1/ξ − 1/(1 +ξ )

]

However, at equilibrium 1/ξ = exp(K/RT) − 1; 1/(1 + ξ ) = [exp(K /RT) − 1]/

exp(K /RT).

Thus, B =+RT[1/ξ − 1/(1 + ξ )] = RT[1 − exp(K /RT)]

/ exp(K /RT).

This is always positive. The state of equilibrium must be stable.

1.9 Combined ﬁrst and second law 21

1.9 Combined ﬁrst and second law

Combination of the ﬁrst and second laws, Eqs (1.11) and (1.38) yield by elimination of

dQ,

dS = dQ/T + S

dN + d

S + (dU − dQ − dW − H

dN)/ T

= dU/T + (S

− H

/T )dN − dW/T + d

S. (1.47)

Denoting H

− TS

by G

,asymbol that will be explained in Section 3.2, and intro-

ducing Ddξ/T for d

S from Eq. (1.43) and only considering compression work, we

obtain

dS = (1/T )dU + (P/T )dV − (G

/T )dN + Ddξ/T. (1.48)

It should be noted that the alternative deﬁnition of heat, Eq. (1.12), would yield the same

result by eliminating dQ

∗

between Eqs (1.13) and (1.39). The combination of the two

laws is due to Gibbs [3] and Eq. (1.48), without the last term is often called Gibbs’

equation or relation. We shall simply refer to Eq. (1.48)asthecombined law and it

can be written in many different forms, expressing one state variable as a function of

the others. Such a function, based on the combined law, is regarded as a characteristic

state function for the set of variables occurring on the right-hand side. The variables in

that set are regarded as the natural variables for the quantity appearing on the left-hand

side.

It is more common to write the combined law in the following form

dU = T dS − PdV + G

dN − Ddξ. (1.49)

Here, U is the characteristic state function and its natural variables are S, V and N. One

usually regards S as an external variable although its value is also inﬂuenced by internal

processes and it is not possible to control its value by actions from the outside without

an intimate knowledge of the properties of the system.

When there are i internal processes, one should replace Ddξ by  D

dξ

.Forthe sake

of simplicity this will be done only when we actually consider more than one process.

By grouping together the products of the external variables in Eq. (1.49)wewrite

dU = Y

− Ddξ, (1.50)

where Y

represents potentials like T.Itisevident that the pressure should be expressed

as −P in order to be comparable with other potentials. As a consequence, we shall plot

P in the negative direction in many diagrams (see, for instance, Fig. 1.1). X

represents

extensive quantities like S and V. The pair of one potential and one extensive quantity,

and X

,iscalled a pair of conjugate variables, for instance T, S or − P, V . Other

pairs of conjugate variables may be included through the ﬁrst law by considering other

types of work, for instance gravitational work. It is important to notice that the change

in U is given in terms of the changes in variables all of which are extensive like S and V

and all of them are subject to the law of additivity.

22 Basic concepts of thermodynamics

Since U is a state variable which is a function of all the external variables, X

, X

etc., and the internal ξ variables, we have



∂U

∂ X



,ξ

, (1.51)

where X

represents all the X variables except for X

.Itisinteresting to note that all the

Y variables are obtained as partial derivatives of an energy with respect to an extensive

variable. That is why they are regarded as potentials. One may also regard − D and ξ as

a pair of conjugate variables where − D is the potential and is obtained as

− D =



∂U

∂ξ



, (1.52)

where X

represents all the X variables. It should be emphasized that the Y potentials

have here been deﬁned for a frozen-in state because ξ was treated as an independent

variable that is kept constant. Under conditions of maintained equilibrium one should

treat ξ as a dependent variable and the potentials are deﬁned as



∂U

∂ X



. (1.53)

We will soon see that for equilibrium states the two deﬁnitions of Y

give the same result.

In the following discussions we do not want to be limited to frozen-in states (dξ = 0),

nor to equilibrium states or reversible changes (D = 0) and we will thus retain the Ddξ

term in the combined law. It should again be emphasized that there are those two different

cases for which the term Ddξ is zero and can be omitted.

The combined law can be expressed in several alternative forms depending upon the

choice of independent external variables. These forms make use of new state functions

which will be discussed soon.

Exercise 1.11

Trytoinclude the effect of electrical work in the combined law.

Hint

There are two cases. First, consider the addition of an extra charge to the system. Second,

consider the case where the system is made part of an electrical circuit.

Solution

In the ﬁrst case, the ﬁrst law gives dU = dQ + dW + dW

where we may write dW

E · d(charge) =−EF dn

,where F is the Faraday constant (the negative of the charge

of one mole of electrons) and n

is the number of extra electrons (in mole). E is the

electrical potential. The combined law becomes dU = T dS − PdV − EFdn

− Ddξ.

However, E increases very rapidly with n

and reaches extremely high values before n

is large enough to have a chemical effect. This form is thus of little practical interest.

1.10 General conditions of equilibrium 23

Let us now consider a system that is part of an electrical circuit. It is evident that

the charge entering a system through one lead must be practically equal to the charge

leaving the system from the other lead, i.e. dn

=−dn

. The ﬁrst law becomes

dU = dQ + dW + dW

= dQ + dW − E

F dn

− E

F dn

= dQ + dW − (E

−

)F dn

, and the combined law becomes dU =T dS − PdV −(E

− E

)

F dn

− Ddξ. E

and E

are the electrical potentials on the two sides of the

system. At this time we do not need to speculate on what happens inside the system.

1.10 General conditions of equilibrium

A system is in a state of equilibrium if the driving forces for all possible internal processes

are zero. Many kinds of internal processes can be imagined in various types of systems

but there is one class of internal process that should always be considered, the transfer of a

quantity of an extensive variable from one part of the system, i.e. a subsystem, to another

subsystem. In this section we shall examine the equilibrium condition for such a process.

Let us ﬁrst examine an internal process taking place in a system under constant values

of the external extensive variables S and V, here collectively denoted by X

, and let us

not be concerned about the experimental difﬁculties encountered in performing such an

experiment. We could then turn to the combined ﬁrst and second law in terms of dU,

which is reduced as follows

dU = Y

− Ddξ =−Ddξ. (1.54)

The driving force for the internal process will be

D =−(∂U/∂ξ)X

. (1.55)

The process can occur spontaneously and proceed until U has reached a minimum. The

state of minimum in U at constant S and V is thus a state of equilibrium.

The internal process we shall now consider is the transfer of dX

from one subsystem

(



)tothe other (



), keeping the remaining Xs constant at different values in the two

subsystems. It is convenient to measure the extent of this internal process by identifying

dξ with −dX

for the ﬁrst subsystem and +dX

for the second. We thus obtain, by

applying the law of additivity to D,

− D =



∂U

∂ξ





∂U

∂(−X

)







∂U

∂ X





=−



∂U

∂ X







∂U

∂ X





(1.56)

The derivative ∂U/∂ X

is identical to the conjugate potential Y

and we thus ﬁnd

D = Y



− Y



. (1.57)

The driving force for this process will be zero and the system will be in equilibrium with

respect to the process if the potential Y

has the same value in the two subsystems. We

have thus proved that each potential must have the same value in the whole system at

24 Basic concepts of thermodynamics

equilibrium. This applies to T, and to P with an exception to be treated in Chapter 16.It

also applies to chemical potentials µ

,which have not yet been introduced.

Exercise 1.12

One may derive a term −EF dn

for the electrical contribution to dU. Here E is the

electrical potential and −F dn

the electrical charge because dn

is the number of moles

of extra electrons and −F is the charge of one mole of electrons. Evaluate the driving

force for the transfer of electrons from one half of the system to the other if their electrical

potentials are E



and E



and can be kept constant. Deﬁne dξ as dn

Solution

−D = (∂U/∂ξ) =−(∂U/∂n

)



+ (∂U/∂n

)



= E



F − E



F ; D = (E



− E



)F .In

practice, the big question is whether the charge transfer will change the potential differ-

ence or whether there is a device for keeping it constant.

1.11 Characteristic state functions

Under experimental conditions of constant S, V and N it is most convenient to use the

combined law in the form given by Eq. (1.49) because then it yields simply

dU =−Ddξ. (1.58)

At equilibrium, D = 0, we obtain

D =−(∂U/∂ξ)

S,V ,N

= 0 (1.59)

for the internal process. If instead D > 0, then the internal process may proceed sponta-

neously and the internal energy will decrease and eventually approach a minimum under

constant S, V and N.

From an experimental point of view it is not very easy to control S but relatively

easy to control T.Achange of independent variable may thus be desirable and it can be

performed by subtracting d(TS)which is equal to T dS + SdT . The combined law in

Eq. (1.49)isthus modiﬁed to

d(U − TS) =−SdT − PdV + G

dN − Ddξ. (1.60)

We may regard this as the combined law for the variables T, V and N and the combination

U − TSis regarded as the characteristic state function for these variables, whereas U is

regarded as the characteristic state function for the variables S and V. The new function