Hillert M. Phase Equilibria, Phase Diagrams and Phase Transformations: Their Thermodynamic Basis

Подождите немного. Документ загружается.

5.3 Alternative methods of transformation 85

through a system where a homogeneous molecular reaction takes place, suggesting that

the two processes could not be coupled. It is an interesting question whether one would

always ﬁnd that there is no coupling if one could really identify the actual processes

on the microscale. If that is the case, then the reciprocal relation should always be a

mathematical consequence of a different choice of processes.

Exercise 5.3

Show how Eq. (5.21) can be derived.

Hint

Start with Eq. (5.16a) and insert in turn Eqs (5.15a) and (5.18).

Solution

∗



∗

;

∗



5.3 Alternative methods of transformation

So far, we have introduced a new set of processes by expressing the new ﬂuxes as linear

combinations of the initial ones. One could just as well express the new forces as linear

combinations of the initial forces

∗

= β

+ β

(5.26a)

∗

= β

+ β

. (5.26b)

The initial processes are still deﬁned by Eqs (5.15)but we shall invert them to make

them consistent with the new way of deﬁning the new processes

= R

+ R

(5.27a)

= R

+ R

. (5.27b)

The R coefﬁcients can be obtained from the L coefﬁcients in Eqs (5.15)bystandard

methods. With a similar procedure as before, one now obtains

∗



∗

(5.28)

∗



. (5.29)

The L

∗

coefﬁcients can be evaluated by inverting Eq. (5.28).

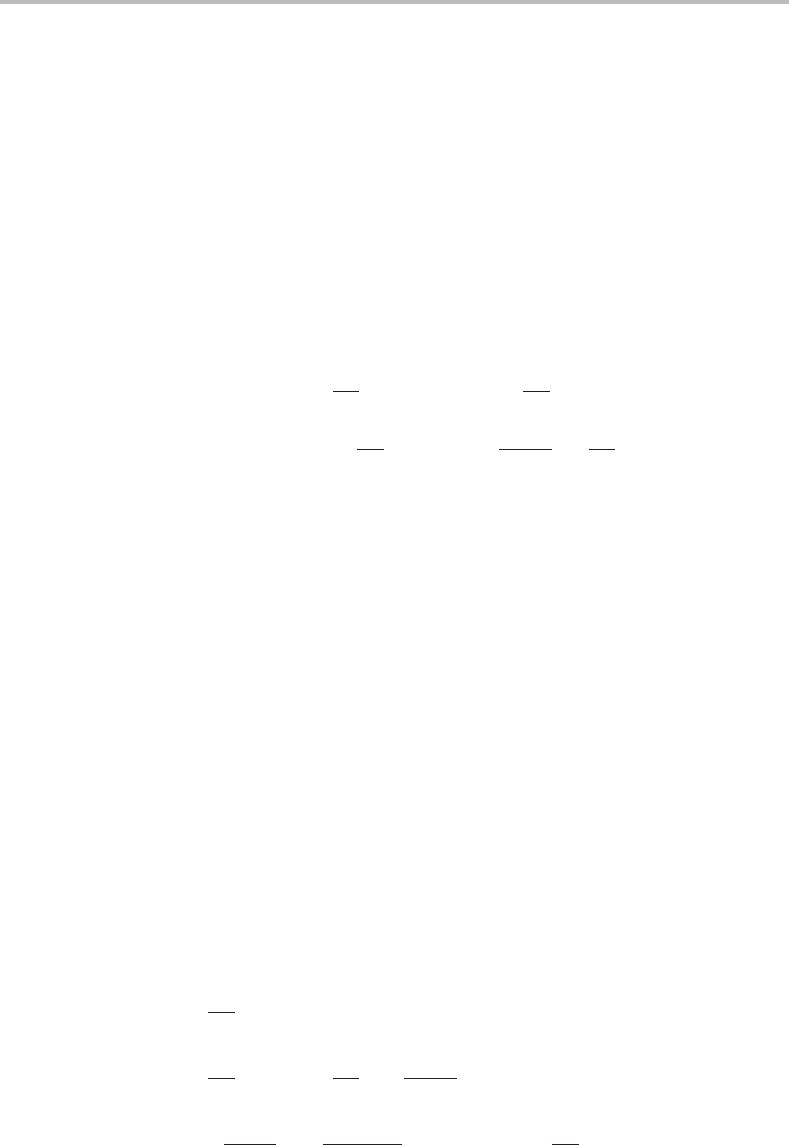
86 Thermodynamics of processes

One may also like to prescribe both ﬂux and force for one process and not make any

prescription for the other process

∗

= α

+ α

(5.30)

∗

= β

+ β

. (5.31)

One should then express J

∗

and X

∗

using the four coefﬁcients deﬁned by these equations.

In general, a complete set of β coefﬁcients can be expressed in terms of the α coefﬁcients

by inverting Eqs (5.18)

/β

=−α

/β

=−α

/β

= α

/β

= α

− α

. (5.32)

For the second process one could thus write

∗

= α

+ α

= α



+ J



= α



−

+ J



(5.33)

∗

= β

+ β

= β



−

+ X





−

+ X



. (5.34)

In these expressions only α

was not given by Eqs (5.30) and (5.31). However, α

eliminated in the product J

∗

and, as in the discussion following Eq. (5.23), it may

thus be regarded as a trivial factor for the second new process. It may thus be concluded

that in order for a new process, deﬁned by its ﬂux and force, to be part of a new set of

conjugate processes it must be combined with a unique partner deﬁned by Eqs (5.33)

and (5.34).

Finally, it may happen that for some particular reason one would like to prescribe the

ﬂux for a new process but the force for the other process.

∗

= β

+ β

(5.35)

∗

= α

+ α

. (5.36)

Again, the α and β coefﬁcients are related by Eq. (5.32)but this time only three of the

coefﬁcients given by the initial equations are independent. Let α

be the dependent one.

Eq. (5.32) yields

=−α

/β

. (5.37)

This must be satisﬁed when the initial equations, Eqs (5.35) and (5.36) are formulated.

As a compensation, there is a degree of freedom when evaluating the remaining four

coefﬁcients. Lets us choose α

as the arbitrary parameter. Eq. (5.32)would then yield

(5.38)



−



(

− 1

)

(5.39)

=−

(

− 1

)

=−

(

− 1

)

. (5.40)

An application of this kind of transformation will be given in Section 17.5.

5.3 Alternative methods of transformation 87

So far, we have always transformed the initial set of processes into the same number

of new processes. However, there are cases where the new set will contain one process

more or one less. When transforming the phenomenological equations for diffusion in

order to change the frame of reference, one often introduces a set with one process less.

That case will be discussed in Section 5.8.Acase with an increase of the number of

processes will now be described.

It may happen that one describes the development of a system with a set of processes

that one is convinced are those that actually take place on a microscale. Nevertheless,

experimental measurements have yielded cross coefﬁcients. There is thus a coupling

between the processes but it is possible that it may be caused by an additional process

that was not considered primarily because it was formally possible to represent the exper-

imental information without using it. By introducing the phenomenological equation for

that process into the representation of experimental information, it is possible that the

cross coefﬁcients decrease in value or even become negligible. If several additional pro-

cesses seem possible, one may decide to use the one giving the lowest cross coefﬁcients.

That one would then be regarded as the coupling process.

Suppose one has studied two processes ﬁnding that they are coupled as described by

= L

= 0intheir phenomenological equations,

= L

+ L

(5.41a)

= L

+ L

. (5.41b)

With these equations one has thus been able to give an adequate description of how the

system develops. However, one is convinced that the two processes actually occur in

the system and feels that they should be independent of each other if it were not for

the presence of a third process that is responsible for the coupling. Assuming that there

should be no cross terms if the system is represented by all three processes one would

write

∗

= L

∗

(5.42a)

∗

= L

∗

(5.42b)

∗

= L

∗

. (5.42c)

It should be noticed that it is necessary to redeﬁne the ﬂuxes of the two initial processes

when the third one is introduced even though those processes are the same as before and

should still have the same forces.

∗

= X

(5.43a)

∗

= X

. (5.43b)

Of course, there should be some relation between the third process and the initial ones

because an adequate description of the system can be given already by the initial ones.

Suppose the relation is

∗

= kX

+lX

= kX

∗

+lX

∗

. (5.44)

88 Thermodynamics of processes

The entropy production must be the same in both descriptions. By eliminating X

∗

one

obtains

σ = J

∗

+ J

∗

+ J

∗

= (J

∗

+ kJ

∗

+ (J

∗

+lJ

∗

= J

+ J

. (5.45)

By inserting Eqs (5.43) one can identify the relations between the two sets of processes

by comparing terms.

= J

∗

+ kJ

∗

(5.46a)

= J

∗

+lJ

∗

. (5.46b)

Introducing the phenomenological equations for the three new processes from Eqs (5.42)

one obtains,

= J

∗

+ kJ

∗

= L

∗

+ kL

∗

(kX

∗

+lX

∗

) = (L

∗

+ k

∗

+ klL

∗

. (5.47a)

= J

∗

+lJ

∗

= L

∗

+lL

∗

(kX

∗

+lX

∗

) = klL

∗

+ (L

∗

. (5.47b)

It is satisfactory to see that the reciprocal relation is obeyed. Comparison with Eqs (5.41)

yields

= L

∗

+ k

∗

; L

= klL

∗

= L

; L

= L

∗

(5.48)

or inverted,

∗

= L

/kl = L

/kl (5.49a)

∗

= L

−l

/kl = L

− L

l/k (5.49b)

∗

= L

− k

/kl = L

− L

k/l. (5.49c)

The introduction of a third, coupling process is thus another way of describing the

development of the system without any cross terms. The advantage of this method is that

the initial processes will be part of the ﬁnal description. That may be desirable if they

have a strong physical basis.

The fact that it is always possible to introduce a set of processes without cross terms

may be of theoretical interest even without trying to identify their physical background,

as demonstrated by the following example. It may seem self-evident that there could be

no spontaneous processes in a system without any entropy being produced. σ = 0 for

the whole system should thus be a condition of equilibrium for the whole system and for

all parts of it. However, it has been argued that one process having σ

> 0 and another

one having σ

< 0 could together yield σ = 0. On the other hand, the fact that one can

always describe what happens in the system with a set of processes without coupling

proves that there is no basis for that argument. Each one of those processes will only

be driven by its own thermodynamic force because all cross coefﬁcients are zero. All

those processes will have to give positive contributions to the entropy production if they

progress. One could thus apply the second law to the individual processes if they are

5.4 Basic thermodynamic considerations for processes 89

not coupled. One may conclude that there can be no spontaneous changes in a system if

σ = 0 for the whole system.

Exercise 5.4

In an attempt to eliminate the cross terms in two processes one introduces a third process

by requiring that (1) J

= J

∗

+ J

∗

and (2) J

= J

∗

− J

∗

.Evaluate the L* coefﬁcients

if this is possible.

Hint

Start by ﬁnding the condition for preserving the rate of entropy production.

Solution

σ = J

∗

+ J

∗

+ J

∗

= J

+ J

= (J

∗

+ J

∗

+(J

∗

− J

∗

= J

∗

+ J

∗

− X

), which yields X

∗

= X

; X

∗

= X

; X

∗

= X

− X

Insert Eqs (5.42)inEq. (1) or (2): J

= J

∗

+ J

∗

= L

∗

+ L

∗

= L

∗

− X

) = (L

∗

+ L

∗

− L

∗

; J

= J

∗

− J

∗

= L

∗

− L

∗

= L

∗

−

∗

− X

) =−L

∗

+ (L

∗

+ L

∗

Comparison with Eqs (5.41) yields L

= L

∗

+ L

∗

; L

=−L

∗

= L

;

= L

∗

+ L

∗

or inverted: L

∗

=−L

; L

∗

= L

− L

∗

= L

+ L

;

∗

= L

− L

∗

= L

+ L

5.4 Basic thermodynamic considerations for processes

In order to apply thermodynamics to the kinetics of processes, one must be aware of some

fundamental principles and new assumptions must be made. For inhomogeneous systems

the basic extensive quantities, N

, U, V and S are obtained by integration of the local

value of the corresponding intensive property, usually expressed by the molar quantity.

It is thus necessary to assume that one can deﬁne the local value of those quantities. The

molar quantity is not just an average over a larger system. It is an intensive quantity and

depends on the local values of T, P and composition and also on the arrangement of the

atoms. However, it may also depend on the gradient of those quantities. There are no

gradient effects in a homogeneous system and in the present work they will be neglected

for inhomogeneous systems unless speciﬁcally stated. An exception is the treatment

of a phenomenon called spinodal decomposition for which important restrictions are

described by including the effect of composition gradients on the Gibbs energy. See

Section 15.4.

, U and V obey the law of additivity and their values in a system are conserved

quantities in the sense that they can only change by interaction with the surroundings.

Their values for the whole system are thus conserved if there is no exchange of heat, work

or volume with the surroundings. The entropy, S, can change by internal processes but

90 Thermodynamics of processes

S − 

S is a conserved quantity if 

S is deﬁned as the internally produced entropy.

Other extensive quantities are derived from the primary ones by adding or subtracting

terms containing P, T and µ

, e.g. the terms PV and TS. The law of additivity applies to

such quantities only under special precautions as discussed in Section 3.4.

Finally, it should be noted that, when applying thermodynamics to systems with inter-

nal processes, one assumes that thermodynamic properties, evaluated under equilibrium

or frozen-in conditions, apply not only to stable and metastable systems but also to unsta-

ble systems undergoing changes. In the present work that assumption will be applied as an

approximation without further discussion. We shall for instance evaluate thermodynamic

properties by assuming that any momentary situation is frozen-in.

Most of the applications in this chapter are based on the combined law in the form

dS = (1/T )dU + (P/T )dV − (µ

/T )dN

+ d

S, (5.50)

where d

S is the entropy production which must be positive for a system undergoing

spontaneous changes. We shall ﬁrst consider cases where d

S is caused by homogeneous

processes that will not disturb the uniformity of a system which is uniform from the

beginning. Transport processes require a quite different approach. They concern quanti-

ties that can be exchanged with the surroundings and in the limit they could sometimes

establish a stationary state of ﬂow through the system. Even though such processes may

concern quantities already present in the combined law, it should be realized that in the

combined law they represent direct exchanges with the surroundings and not processes

of ﬂow inside the system. The discussion of transport processes will thus be preceded

by considering a discontinuous system composed of two subsystems and with transport

between them.

Starting with processes in homogeneous systems we shall presume that all thermo-

dynamic properties are uniform. Internal processes may tend to change some properties

but the processes must progress uniformly in the whole system in order not to change the

homogeneous character. In a system that is not completely isolated there may be compli-

cations, e.g. due to the heat of reaction leaking out to the surroundings and causing heat

ﬂow from the interior of the system to its surface. In a system open for heat transfer to

a reservoir of constant temperature it is common to assume that the temperature is kept

constant although there must be temperature gradients in order for the heat of reaction

to leave the system. Evidently, one assumes that those gradients and the corresponding

thermodynamic forces for the heat ﬂow are so small that their production of entropy is

negligible. That will now be our assumption.

It may often be more convenient to use the combined law in the form based on Gibbs

energy if T and P are kept constant. By further assuming that there is no exchange of

matter with the surroundings we get for spontaneous changes of the state,

dG = V dP − SdT + µ

− T d

S =−T d

S =− D

dξ

< 0. (5.51)

is the driving force for process j.Itisdeﬁned as a generalization of the driving force,

D,inSection 1.8.

≡ T

∂

∂ξ

=−

∂G

∂ξ

. (5.52)

5.4 Basic thermodynamic considerations for processes 91

Introducing the ﬂux of process j, J

= dξ

/dt,weget for the time derivative

−

G = T

= T σ =  D

> 0. (5.53)

The rate of entropy production, σ ,was deﬁned by Eq. (5.3) and the second law requires

that it is positive. That explains why dG in Eq. (5.51)was stated as negative. It should

be emphasized that the driving force is only deﬁned for constant T and is then related to

the more generally applicable thermodynamic force X

= TX

. (5.54)

That is shown by comparison with Eq. (5.7). The term driving force for D

is here used

in an attempt to avoid confusion with the thermodynamic force, X

The internal production of entropy, σ ,isawell deﬁned quantity and T σ is regarded

as the dissipation of Gibbs energy. It is thus connected to the internal processes. On the

other hand, −

G in Eq. (5.53) describes the change of the properties of the system with

no regard to how the change occurred. The equality of the two may seem self-evident

but is extremely useful and may be illustrated in diagrams of the molar Gibbs energy

versus molar content. Then it is necessary to express both the dissipation and the change

of Gibbs energy in the same dimensions as the diagram, i.e. J/mol. Equation (5.53)is

expressed in J/s and it would thus be necessary to divide the whole equation by some

ﬂux, J

, measured as mol/s. One would then obtain the change of Gibbs energy per mole

of the ﬂux,

− G

=−

G/J

=  f

, (5.55)

where f

≡ J

.For simple case with just one process, J

will normally be deﬁned as

the ﬂux of that process and −G

will be equal to D

. One can then evaluate the driving

force D

from −G

and it is even common to regard it as the driving force itself. For

more complicated cases one may even regard it as the total driving force. However, it

should be remembered that −G

is the change of the properties of the system and D

or f

represents dissipation.

There are many kinds of homogeneous processes, some of which can be described as

a change of order, e.g., short-range order of the atoms relative to each other and even the

transition to a state of long-range order if it occurs by a so-called second-order transition,

which is homogeneous. An extreme case of order among the atoms is the formation of

molecules by so-called chemical reactions. They will be treated separately in the next

section.

Exercise 5.5

Suppose T and V are kept constant. What form of the combined law should it then be

natural to use? How would the time derivative of that characteristic state function be

related to the rate of entropy production if there is no exchange of matter?

92 Thermodynamics of processes

Solution

Using Helmholtz energy, the combined law is written as dF =−V dP − SdT +

µ

− T d

S =−T d

S =− D

dξ

< 0. The time derivative of Helmholtz

energy is the same as of Gibbs energy but the conditions are different −

F = T d

S/dt =

T σ =  D

> 0.

5.5 Homogeneous chemical reactions

The combined law for dG contains the terms µ

where the summation includes

a set of c components. Each one is regarded as independent if it cannot be formed by a

reaction between the other ones. Basically, the set should only contain the c independent

components. For homogeneous chemical reactions one sometimes includes more com-

ponents. One may then choose which ones should be regarded as independent. The other

ones will be regarded as dependent and each one of them can be formed by a reaction

between the independent ones. Those reactions are regarded as independent reactions

but many more reactions could occur between the components. If one considers s com-

ponents altogether, there will be (s − c) dependent components and the same number of

independent reactions. That number will be represented by r = s − c.

A component could be a pure element but could also be a molecule or some hypo-

thetical aggregate of atoms. Let us express the chemical composition of component j by

the letter J and write

J =



i=1

I , (5.56)

where a

represents the stoichiometric coefﬁcients and I represents a pure element

or the composition of any other basic unit used for representing the composition of

the components. Let these units be the independent components and J be a dependent

component. It is evident that Eq. (5.56) should then be the reaction formula for the

formation of J if it is turned around.



i=1

I = J. (5.57)

We could thus regard the a

coefﬁcients as the reaction coefﬁcients for the reaction

between J and the c independent components. They have here been normalized by

making the coefﬁcient for J equal to 1. There will be such a reaction for each dependent

component, i.e. r reactions. They may be chosen as the r independent reactions among

the many more possible reactions between the s components.

One reason to include dependent components in µ

is that it may facilitate

the modelling of the thermodynamic properties, e.g. for a gas containing several kinds

of molecules. A related reason is that one may like to consider frozen-in states where

the rates of internal reactions are negligible. In that case one may add some amount of

any component without having to consider its possible reactions with other components

5.5 Homogeneous chemical reactions 93

inside the system. The dependent components can then be treated as independent and

we may deﬁne the chemical potential of any component



∂G

∂ N



T,P,N

. (5.58)

Even though the system is frozen-in, we may evaluate the driving force for the r reactions

by which each one of the r additional components could react with the independent ones.

It may be derived as follows.

Considering the changes of all the s components, both independent and dependent

ones, we may write the combined law as

dG = V dP − SdT +



i=1

(5.59)

We would now like to introduce the extent of the internal reactions, ξ

,inthis equation.

One may deﬁne the reactions in such a way that each reaction represents the formation

of a single dependent component from the set of independent ones, but without the other

dependent components being involved. In a closed system, the change of an independent

component may be given by the loss caused by several reactions, and may thus be related

to the increase of several dependent components.

=−



j=1

. (5.60)

For the dependent components dN

is only caused by their own independent reactions.

The combined law for a closed isobarothermal system will thus be

dG = V dP − SdT +



i=1



−



j=1





j=1

= V dP − SdT −



j=1

dξ

. (5.61)

The driving force for the formation of the dependent component j is here deﬁned as



i=1





− µ

. (5.62)

The combined law for an open system could thus be written

dG = V dP − SdT +



i=1



j=1

−



j=1

dξ

. (5.63)

It should be emphasized that dN

and dN

here represent only the amounts received from

the surroundings. The changes due to all internal reactions are included in dξ

. Under

freezing-in conditions one should omit  D

dξ

. When the internal reactions are very

fast, there is almost internal equilibrium and the driving forces necessary for maintaining

94 Thermodynamics of processes

equilibrium are so small that  D

dξ

can again be omitted. Then



i=1

(5.64)

dG = V dP − SdT +



i=1





j=1



. (5.65)

Again, dN

and dN

represent only the amounts received from the surroundings. When

treating intermediate cases one should take into account the rate of all reactions, starting

with the r reactions by which the r dependent components can form from the independent

ones and then adding those in which two or more of the dependent ones take part. We

shall now consider the very simplest case where there are one independent component

and two dependent ones. The dependent components will be denoted by 1 and 2 and

their reactions will also be identiﬁed by 1 and 2. For consistency with the derivations in

Section 5.4 the superscripts used for D and ξ in the above equations will now be given

as subscripts. Without any coupling between the ﬁrst two reactions their rates will thus

be given as

∗

dξ

= L

∗

= K

∗

(5.66)

∗

dξ

= L

∗

= K

∗

, (5.67)

where D

∗

= TX

∗

according to Eq. (5.54) and K

∗

= L

∗

/T .For the additional reaction,

where both dependent components take part, we write

∗

dξ

= L

∗

= K

∗

. (5.68)

Suppose this reaction produces component 1 and consumes component 2. Then we know

that its driving force must be

∗

= D

∗

− D

∗

. (5.69)

By direct measurements of the amounts of the two dependent components one would not

get any direct information on the third reaction but one can represent the experimental

information using the phenomenological equations for those reactions.

= K

+ K

(5.70a)

= K

+ K

. (5.70b)

The goal is to evaluate the kinetic coefﬁcients in the three processes, assumed to have no

cross terms, from the experimentally determined coefﬁcients in Eqs (5.70a and b). This

problem was discussed in more general terms in Section 5.2.Bycomparing the relations

between the driving forces given by Eqs (5.44) and (5.69)weﬁnd that the present case

corresponds to k = 1 and l =−1. From Eq. (5.49)wethus ﬁnd

∗

=−K

; K

∗

= K

+ K

; K

∗

= K

+ K

(5.71)