Hibbeler R.C. Structural Analysis

Подождите немного. Документ загружается.

150 CHAPTER 4INTERNAL LOADINGS DEVELOPED IN S TRUCTURAL MEMBERS

4.3 Shear and Moment Diagrams

for a Beam

If the variations of V and M as functions of x obtained in Sec. 4–2 are

plotted, the graphs are termed the shear diagram and moment diagram,

respectively. In cases where a beam is subjected to several concentrated

forces, couples, and distributed loads, plotting V and M versus x can

become quite tedious since several functions must be plotted. In this

section a simpler method for constructing these diagrams is discussed—a

method based on differential relations that exist between the load, shear,

and moment.

To derive these relations, consider the beam AD in Fig. 4–9a, which is

subjected to an arbitrary distributed loading and a series of

concentrated forces and couples. In the following discussion, the

distributed load will be considered positive when the loading acts upward

as shown. We will consider the free-body diagram for a small segment of

the beam having a length Fig. 4–9b. Since this segment has been chosen

at a point x along the beam that is not subjected to a concentrated force

or couple, any results obtained will not apply at points of concentrated

loading.The internal shear force and bending moment shown on the free-

body diagram are assumed to act in the positive direction according to the

established sign convention, Fig. 4–1. Note that both the shear force and

moment acting on the right face must be increased by a small, finite

amount in order to keep the segment in equilibrium. The distributed

loading has been replaced by a concentrated force that acts at a

fractional distance from the right end, where (For

example, if w(x) is uniform or constant, then will act at so

.) Applying the equations of equilibrium, we have

¢M = V¢x + w1x2 P1¢x2

-V¢x - M - w1x2 ¢x P1¢x2+ 1M +¢M2= 0d+©M

= 0;

¢V = w1x2 ¢x

V + w1x2 ¢x - 1V +¢V2= 0+

©F

= 0;

¢x,w1x2¢x

0 6P61.P1¢x2

w1x2¢x

¢x,

w = w1x2

B C

x

w  w(x)

(a)

x

V  V

(b)

w(x)x

w(x)

M  M

P (x)

Fig. 4–9

The many concentrated loadings acting

on this reinforced concrete beam create a

variation of the internal loading in the

beam. For this reason, the shear and moment

diagrams must be drawn in order to properly

design the beam.

4.3 SHEAR AND MOMENT DIAGRAMS FOR A BEAM 151

Dividing by and taking the limit as these equations become

(4–1)

(4–2)

As noted, Eq. 4–1 states that the slope of the shear diagram at a point

(dV兾dx) is equal to the intensity of the distributed load w(x) at the point.

Likewise, Eq. 4–2 states that the slope of the moment diagram (dM兾dx) is

equal to the intensity of the shear at the point.

Equations 4–1 and 4–2 can be “integrated” from one point to another

between concentrated forces or couples (such as from B to C in Fig. 4–9a),

in which case

(4–3)

and

(4–4)

As noted, Eq. 4–3 states that the change in the shear between any two

points on a beam equals the area under the distributed loading diagram

between the points. Likewise, Eq. 4–4 states that the change in the moment

between the two points equals the area under the shear diagram between

the points. If the areas under the load and shear diagrams are easy to

compute, Eqs. 4–3 and 4–4 provide a method for determining the numerical

values of the shear and moment at various points along a beam.

Change in

Moment

f = e

Area under

Shear Diagram

¢M =

V1x2 dx

Change in

Shear

f = c

Area under

Distributed Loading

Diagram

¢V =

w1x2 dx

Slope of

Moment Diagram

f = 5Shear

= V

Slope of

Shear Diagram

f = e

Intensity of

Distributed Load

= w1x2

¢x : 0,¢x

152 CHAPTER 4INTERNAL LOADINGS DEVELOPED IN S TRUCTURAL MEMBERS

From the derivation it should be noted that Eqs. 4–1 and 4–3 cannot be

used at points where a concentrated force acts, since these equations do

not account for the sudden change in shear at these points. Similarly,

because of a discontinuity of moment, Eqs. 4–2 and 4–4 cannot be used at

points where a couple moment is applied. In order to account for these

two cases, we must consider the free-body diagrams of differential

elements of the beam in Fig. 4–9a which are located at concentrated

force and couple moments. Examples of these elements are shown in

Figs. 4–10a and 4–10b, respectively. From Fig. 4–10a it is seen that force

equilibrium requires the change in shear to be

(4–5)

Thus, when F acts downward on the beam, is negative so that the shear

diagram shows a “jump” downward. Likewise, if F acts upward, the jump

is upward. From Fig. 4–10b, letting moment equilibrium

requires the change in moment to be

(4–6)

In this case, if an external couple moment is applied clockwise,

is positive, so that the moment diagram jumps upward, and when M acts

counterclockwise, the jump must be downward.1¢M2

¢M M¿

¢M = M¿d+©M

= 0;

¢x : 0,1¢V2

¢V

¢V =-F+

©F

= 0;

V  V

M  M

(a)

x

M¿

 x

V  V

(b)

M  M

Fig. 4–10

4.3 SHEAR AND MOMENT DIAGRAMS FOR A BEAM 153

Procedure for Analysis

The following procedure provides a method for constructing the shear

and moment diagrams for a beam using Eqs. 4–1 through 4–6.

Support Reactions

• Determine the support reactions and resolve the forces acting on

the beam into components which are perpendicular and parallel

to the beam’s axis.

Shear Diagram

• Establish the V and x axes and plot the values of the shear at the

two ends of the beam.

• Since the slope of the shear diagram at any point is

equal to the intensity of the distributed loading at the point. (Note

that w is positive when it acts upward.)

• If a numerical value of the shear is to be determined at the point,

one can find this value either by using the method of sections as

discussed in Sec. 4–1 or by using Eq. 4–3, which states that the

change in the shear force is equal to the area under the distributed

loading diagram.

• Since w(x) is integrated to obtain V, if w(x) is a curve of degree n,

then V(x) will be a curve of degree For example, if w(x) is

uniform, V(x) will be linear.

Moment Diagram

• Establish the M and x axes and plot the values of the moment at

the ends of the beam.

• Since the slope of the moment diagram at any point

is equal to the intensity of the shear at the point.

• At the point where the shear is zero, and therefore

this may be a point of maximum or minimum moment.

• If the numerical value of the moment is to be determined at a

point, one can find this value either by using the method of

sections as discussed in Sec. 4–1 or by using Eq. 4–4, which states

that the change in the moment is equal to the area under the shear

diagram.

• Since V(x) is integrated to obtain M, if V(x) is a curve of degree n,

then M(x) will be a curve of degree For example, if V(x) is

linear, M(x) will be parabolic.

n + 1.

dM>dx = 0,

dM>dx = V,

n + 1.

dV>dx = w,

154 CHAPTER 4INTERNAL LOADINGS DEVELOPED IN S TRUCTURAL MEMBERS

The two horizontal members of the power line support frame are

subjected to the cable loadings shown in Fig. 4–11a. Draw the shear

and moment diagrams for each member.

SOLUTION

Support Reactions. Each pole exerts a force of 6 kN on each

member as shown on the free-body diagram.

Shear Diagram. The end points and

are plotted first, Fig. 4–11b.As indicated, the shear between

each concentrated force is constant since The shear

just to the right of point B (or C and D) can be determined by the

method of sections, Fig. 4–11d.The shear diagram can also be established

by “following the load” on the free-body diagram. Beginning at A the

4 kN load acts downward so No load acts between A

and B so the shear is constant. At B the 6 kN force acts upward, so the

shear jumps up 6 kN, from to , etc.

Moment Diagram. The moment at the end points and

is plotted first, Fig. 4–11c. The slope of the moment

diagram within each 1.5-m-long region is constant because V is

constant. Specific values of the moment, such as at C, can be deter-

mined by the method of sections, Fig. 4–11d, or by finding the change

in moment by the area under the shear diagram. For example, since

at A, then at C,

.=-3 kN

m+ 211.52

0 + 1-4211.52=M

= M

+¢M

= 0

x = 6 m, M = 0

x = 0, M = 0

+2 kN-4 kN

=-4 kN.

w = dV>dx = 0.

V = 4 kN

x = 6 m,x = 0, V =-4 kN

EXAMPLE 4.7

6 kN6 kN

4 kN 4 kN4 kN

1.5 m 1.5 m 1.5 m 1.5 m

(c)

(b)

(a)

1.5

6 6

3

2

4

4.5 6

x (m)

M (kNm)

31.5 4.5 6

x (m)

V (kN)

ABCDE

V negative constant

M slope negative constant

V positive constant

M slope positive constant

w  0

V slope  0

w  0

V slope  0

6 kN

4 kN

1.5 m 1.5 m

(d)

Fig. 4–11

4.3 SHEAR AND MOMENT DIAGRAMS FOR A BEAM 155

EXAMPLE 4.8

Draw the shear and moment diagrams for the beam in Fig. 4–12a.

9 m

20 kN/m

(a)

V (kN)

⫺60

x (m)

(c)

5.20 m

20 kN/m

(b)

30 kN 60 kN

104

M (kN⭈ m)

x (m)

(d)

V positive decreasing

M slope positive decreasing

w negative increasing

V slope negative increasing

V negative increasing

M slope negative increasing

Fig. 4–12

SOLUTION

Support Reactions. The reactions have been calculated and are

shown on the free-body diagram of the beam, Fig. 4–12b.

Shear Diagram. The end points and

are first plotted. Note that the shear diagram starts

with zero slope since at and ends with a slope of

The point of zero shear can be found by using the method of

sections from a beam segment of length x, Fig. 4–12e.We require

so that

Moment Diagram. For the value of shear is

positive but decreasing and so the slope of the moment diagram is also

positive and decreasing At

Likewise for the shear and so the slope of the

moment diagram are negative increasing as indicated.

The maximum value of moment is at since

at this point, Fig. 4–12d. From the free-body diagram in

Fig. 4–12e we have

M = 104 kN

-3015.202+

c20a

5.20

bd15.202a

5.20

b + M = 0d +©M

= 0;

V = 0

dM>dx =x = 5.20 m

5.20 m 6 x 6 9 m,

dM>dx = 0.x = 5.20 m,1dM>dx = V2.

0 6 x 6 5.20 m

30 -

c20a

bdx = 0

x = 5.20 m+

©F

= 0;

V = 0,

w =-20 kN/m.

x = 0,w = 0

V =-60 kN

x = 9 m,V =+30 kNx = 0,

(e)

30 kN

[20 ( )]x

—

20 ( )

—

156 CHAPTER 4INTERNAL LOADINGS DEVELOPED IN S TRUCTURAL MEMBERS

Draw the shear and moment diagrams for the beam shown in Fig. 4–13a.

SOLUTION

Support Reactions. The reactions are calculated and indicated on

the free-body diagram.

Shear Diagram. The values of the shear at the end points A

and B are plotted. At C the shear is

discontinuous since there is a concentrated force of 600 lb there. The

value of the shear just to the right of C can be found by sectioning

the beam at this point. This yields the free-body diagram shown in

equilibrium in Fig. 4–13e. This point is plotted on the

shear diagram. Notice that no jump or discontinuity in shear occurs

at D, the point where the couple moment is applied,

Fig. 4–13b.

Moment Diagram. The moment at each end of the beam is zero,

Fig. 4–13d. The value of the moment at C can be determined by the

method of sections, Fig. 4–13e, or by finding the area under the shear

diagram between A and C. Since

Also, since the moment at D is

A jump occurs at point D due to the couple moment of

The method of sections, Fig. 4–13f, gives a value of just to

the right of D.

+2500 lb

4000 lb

ft.

=-1500 lb

= M

+¢M

= 1000 lb

ft + 1-500 lb215 ft2

= 1000 lb

ft,

= 1000 lb

= M

+¢M

= 0 + 1100 lb)(10 ft)

= 0,

4000-lb

1V =-500 lb2

=-500 lb21V

=+100 lb2

EXAMPLE 4.9

10 ft

5 ft

600 lb

4000 lb⭈ft

(a)

V negative constant

M slope negative constant

V (lb)

100

x (ft)

⫺500

(c)

10 ft 5 ft

600 lb

4000 lb⭈ft

100 lb 500 lb

(b)

5 ft

M (lb⭈ft)

2500

⫺1500

1000

(d)

x (ft)

w =0

slope =0

10 ft

600 lb

1000 lb⭈ft

100 lb

(e)

⫺500 lb

10 ft 5 ft

600 lb

100 lb

(f)

2500 lb⭈ft

⫺500 lb

4000 lb⭈ft

Fig. 4–13

4.3 SHEAR AND MOMENT DIAGRAMS FOR A BEAM 157

EXAMPLE 4.10

Draw the shear and moment diagrams for each of the beams shown in

Fig. 4–14.

SOLUTION

In each case the support reactions have been calculated and are

shown in the top figures. Following the techniques outlined in the pre-

vious examples, the shear and moment diagrams are shown under

each beam. Carefully notice how they were established, based on the

slope and moment, where and Calculated

values are found using the method of sections or finding the areas

under the load or shear diagrams.

dM>dx = V.dV>dx = w

3 m

9 kN 9 kN

6 kN/m

3 m

x (m)

V (kN)

M (kN⭈m)

–9

(a)

w negative increasing

V slope negative increasing

V negative increasing

M slope negative increasing

4 ft

6 k/ft

15 k

8 k

47 k

4 ft

(c)

⫺80

⫺20

x (ft)

M (k⭈ft)

20 k⭈ft

⫺15

x (ft)

V (k)

V positive decreasing

M slope positive decreasing

w negative constant

V slope negative constant

3 m

30 kN

8 kN/m

1.5 m

42 kN⭈m

15 kN⭈m

2.64

⫺42

⫺30

⫺6

1.5

4.5

x (m)

V (kN)

M (kN⭈m)

(b)

w negative increasing

V slope negative increasing

V negative increasing

M slope negative increasing

Fig. 4–14

158 CHAPTER 4INTERNAL LOADINGS DEVELOPED IN S TRUCTURAL MEMBERS

Fig. 4–15

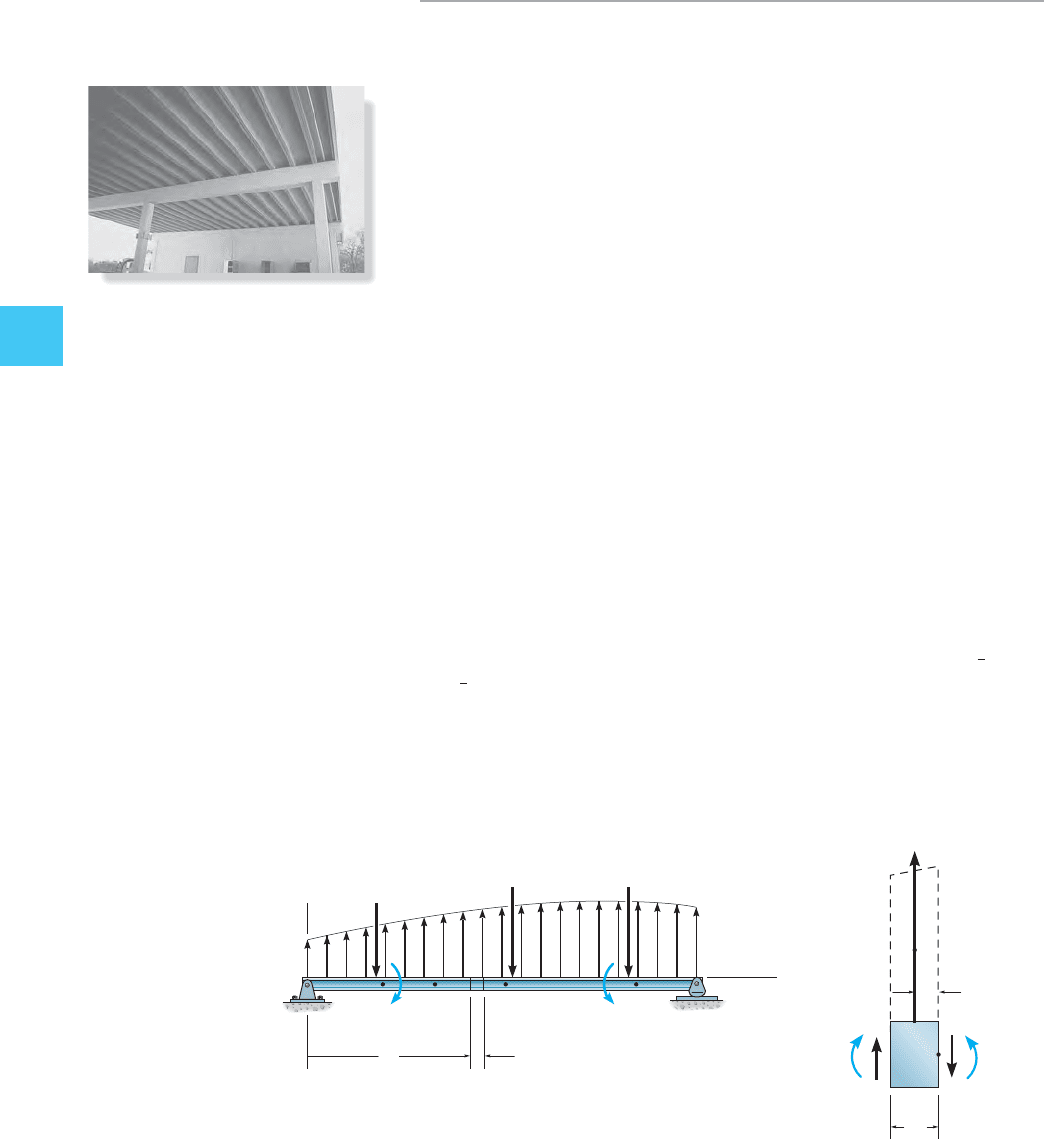
The beam shown in the photo is used to support a portion of the

overhang for the entranceway of the building.The idealized model for

the beam with the load acting on it is shown in Fig. 4–15a. Assume B is

a roller and C is pinned. Draw the shear and moment diagrams for the

beam.

SOLUTION

Support Reactions. The reactions are calculated in the usual

manner.The results are shown in Fig. 4–15b.

Shear Diagram. The shear at the ends of the beam is plotted first,

i.e., and Fig. 4–15c.To find the shear to the left

of B use the method of sections for segment AB, or calculate the area

under the distributed loading diagram, i.e.,

The support reaction causes the shear to jump up

The point of zero shear can be determined

from the slope or by proportional triangles,

Notice how the V diagram follows the

negative slope, defined by the constant negative distributed loading.

Moment Diagram. The moment at the end points is plotted first,

Fig. 4–15d. The values of and 0.239 on the

moment diagram can be calculated by the method of sections, or by

finding the areas under the shear diagram. For example,

Likewise,

show that the maximum positive moment is Notice

how the M diagram is formed, by following the slope, defined by the

V diagram.

0.239 kN

=-2.81 kN

m.M

- 0 =

1-7.50210.752=-2.81,

¢M =

-2.81M

= M

= 0,

x = 0.781 m.2.19>11 - x2,

7.81>x =-10 kN>m,

-7.50 + 15.31 = 7.81 kN.

=-7.50 kN.

¢V = V

- 0 =-1010.752,

=-2.19 kN,V

= 0

EXAMPLE 4.11

0.75 m

10 kN/m

1 m

(a)

0.75 m

10 kN/m

1 m

2.19 kN15.31 kN

(b)

x (m)

V (kN)

⫺7.50

⫺2.19

7.81

0.781 m

(c)

⫺2.81

0.239

x (m)

M (kN⭈m)

(

)

4.3 SHEAR AND MOMENT DIAGRAMS FOR A BEAM 159

EXAMPLE 4.12

Draw the shear and moment diagrams for the compound beam shown

in Fig. 4–16a.Assume the supports at A and C are rollers and B and E

are pin connections.

SOLUTION

Support Reactions. Once the beam segments are disconnected

from the pin at B, the support reactions can be calculated as shown in

Fig. 4–16b.

Shear Diagram. As usual, we start by plotting the end shear at A

and E, Fig. 4–16c. The shape of the V diagram is formed by following

its slope, defined by the loading. Try to establish the values of shear

using the appropriate areas under the load diagram (w curve) to find

the change in shear. The zero value for shear at can either be

found by proportional triangles, or by using statics, as was done in

Fig. 4–12e of Example 4–8.

Moment Diagram. The end moments and

are plotted first, Fig. 4–16d. Study the diagram and note how the

various curves are established using Verify the numerical

values for the peaks using statics or by calculating the appropriate

areas under the shear diagram to find the change in moment.

dM>dx = V.

= 0M

= 60 k

x = 2 ft

10 ft 6 ft 4 ft 6 ft

5 k

2 k/ft

3 k/ft

60 k · ft

(a)

6 ft

20 k

5 k

3 k/ft

60 k⭈ft

4 k

16 k

45 k 6 k

(b)

V (k)

10 16 20

⫺16

⫺21

x (ft)

(c)

M (k⭈ ft)

10 16 20

⫺96

⫺180

x (ft)

(d)

Fig. 4–16