Heubach S., Mansour T. Combinatorics of Compositions and Words
Подождите немного. Документ загружается.

Avoidance of Nonsubword Patterns in Compositions 155
occurring between consecutive critical parts are in increasing order, that is, if
K is a b-block and K
is a b
-block with b<b
,thenK K
.
As before, we can be more specific.
Lemma 5.36 Let B = {b
1
,...,b
s
} be an ordered set and κ be a permutation
of B.Letσ ∈AT
B
κ
(21–2) and let σ
u
= κ
i−1
,σ
v
= κ
i
, i =1,...,s− 1 be two
consecutive critical parts in σ.IfK is a b-block in σ
u+1
σ
u+2
···σ
v−1
,then
b = κ
j
for all j =1, 2,...,i− 1 and b ≤ κ
i
.
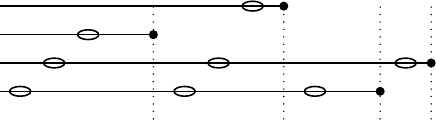
We give an example of the structure diagram for 21–1-avoiding compositions
in Figure 5.5.
1
1
κ
3
2
2X
κ
4
4
4
κ
1
5
5X
κ
2
FIGURE 5.5: Structure diagram for σ ∈AT
B
4512
(21–2).
Using Lemmas 5.35 and 5.36 we obtain the number of b
j
-blocks that occur
in σ ∈AT
B
κ
(21–2).
Lemma 5.37 Let B = {b
1
,...,b
s
} be an ordered set and let κ be a permu-
tation of B.Forσ ∈AT
B
κ
(21–2), the number of κ
j
-blocks in σ is at most
|{i|κ
j
<κ
i
and i<j}| +1.
This result is at first surprising, as it gives the same number of κ
j
-blocks as
for the 12–2-avoiding compositions, even though the conditions for the blocks
are different.
Proof From Lemmas 5.35 and 5.36 we obtain that a κ
j
-block can occur at
most once between two consecutive critical parts κ
i−1
and κ
i
only if i −1 <j
and κ
j
≤ κ
i
. Therefore the number of κ
j
-blocks is
|{i|κ
j
≤ κ
i
and j>i−1}| = |{i|κ
j
≤ κ
i
and j ≥ i}|
= |{i|κ
j
<κ
i
and j>i}|+1,
as claimed. 2
Lemmas 5.34 and 5.37 suggest that there is a bijection between the set of
12–2-avoiding compositions of n with m parts in A and the set of 21–2-avoiding
compositions of n with m parts in A. This is indeed the case.
© 2010 by Taylor and Francis Group, LLC
156 Combinatorics of Compositions and Words
Theorem 5.38 For any ordered set A = {a
1
,a
2
,...}⊆N, 12–2 ∼ 21–2 and
21–1 ∼ 12–1.
Proof Let κ = κ
1
···κ
s
be a permutation of B where B is a fixed subset of
A. It is enough to establish a bijection
ψ
κ
: C
A
n,m
∩AT
B
κ
(12–2) →C
A
n,m
∩AT
B
κ
(21–2)
since each σ has a unique core κ(σ) and set of values B(σ). We will illustrate
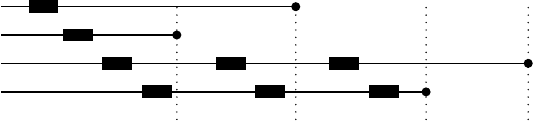
the algorithm with the 12–2-avoiding composition σ = 55441111422251111112.
First we determine the block diagram for the given composition, as shown in
Figure 5.6.
1
1111
∅
11111 1
2
∅
222
∅
2
4
44
4
5
55
5
κ
3
κ
4
κ
1
κ
2
FIGURE 5.6: Block diagram for σ = 55441111422251111112.
The critical parts separate the composition into s sections (the pieces be-
tween the vertical lines in the diagram). In each section, a b
j
-block may
occur (empty or nonempty) as indicated by a rectangle, or is forbidden. Note
that if κ
j
= b
i
j
, then there are exactly j potential locations for a b
i
j
-block.
This is the case for both the 12–2-avoiding and the 21–2-avoiding compo-
sitions if they have the same core. For a given j, not only is the number
of potential occurrences of b
j
-blocks the same, but the number of forbidden
b
j
-blocks is also strictly determined by the core, and thus the same for the
12–2-avoiding and the 21–2-avoiding compositions. This can be seen as fol-
lows. If σ ∈AT
B
κ
(12–2), then there is no forbidden b
j
-block to the left of κ
1
according to Lemma 5.32. In the segment created by κ
i
and κ
i+1
,ab
j
-block
is forbidden if b
j
≥ κ
i
for i =1, 2,...,s− 1. By Lemma 5.36, this forbidden
block corresponds to a forbidden block in the segment created by κ
i−1
and κ
i
in a composition σ
∈AT
B
κ
(21–2) that has the same core, where the section
created by κ
0
and κ
1
is to be interpreted as the section to the left of κ
1
.Fi-
nally, there are no forbidden blocks in the section created by κ
s−1
and κ
s
for
any σ
∈AT
B
κ
(21–2), because there is only one possibility, namely κ
s
-blocks,
which are allowed. Therefore for each b
j
the number of allowable blocks is
identical in σ ∈AT
B
κ
(12–2) and σ
∈AT
B
κ
(21–2) for a given core κ.
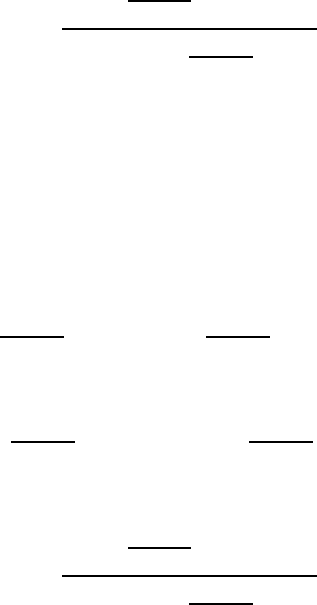
Now we can describe the algorithm. We start with the block diagram for
© 2010 by Taylor and Francis Group, LLC

Avoidance of Nonsubword Patterns in Compositions 157
the composition σ ∈AT
B
κ
(12–2) (see Figure 5.6) and mark the forbidden
block locations with the letter X as shown in Figure 5.7.
1
1111
∅
11111 1
2
∅
222
∅
2
4
44
4
5
55 5
κ
3
κ
4
κ
1
κ
2
X
X
FIGURE 5.7: Modified block diagram for σ = 55441111422251111112.
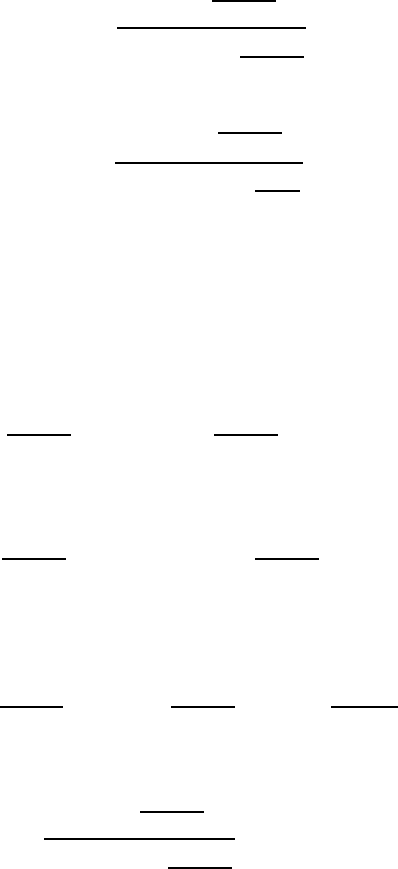
Next we use the structure diagram for the 21–2-avoiding compositions (see
Figure 5.5). For each b
j
we place the allowed (nonempty or empty) blocks
of σ in the allowed positions of the 21–2 structure diagram. For example,
the allowed 1-blocks are 1111, ∅, and 11111, and we place them in the three
allowable 1-block positions of the structure diagram from left to right. For the
5-blocks there is one allowable block, 55, which is placed in the single allowable
position between κ
1
and κ
2
. The resulting 21–1-avoiding composition is σ
=
11114442225551111112, as shown in Figure 5.8.
1
1111
∅
11111 1
2
∅
222
∅
2
4
44
4
5
55 5
κ
3
κ
4
κ
1
κ
2
X
X
FIGURE 5.8: Block diagram for σ
= 11114442225551111112.
Likewise we can create a 12–1-avoiding composition by starting with a 21–1-
avoiding composition and following steps analogous to the ones described
above. Since the structure diagrams uniquely determine the arrangements of
the blocks, ψ
κ
: C
A
n,m
∩AT
B
κ
(12–2) →C
A
n,m
∩AT
B
κ
(21–2) is a bijection. The
Wilf-equivalence 21–1 ∼ 12–1 follows using the complement map. 2
We now derive the generating functions for the five Wilf-equivalence classes.
First we give the results for the three patterns that are in their own equivalence
classes (up to symmetry), namely 11–1, 11–2, and 22–1. For the first pattern
© 2010 by Taylor and Francis Group, LLC
158 Combinatorics of Compositions and Words
we only obtain a recurrence relation, while for the other two patterns we
give explicit formulas for the generating functions which are easy to compute.
Finding an explicit expression for the pattern 11–1 remains an open question
(see Research Direction 5.1).
Theorem 5.39 Let A =[d].Then
AC
11–1
A
(x, y)=
1+
d
i=1
x
2i
y
2
1+x
i
y
AC
11−1
A−{i}
(x, y)
1 −
d
i=1
x
i
y
1+x
i
y
.
Proof Considering the compositions that start with i,weobtain
AC
11−1
A
(i|x, y)
= x
i
y +
j=i
AC
11−1
A
(ij|x, y)+AC
11−1
A
(ii|x, y)
= x
i
y(AC
11−1
A
(x, y) − AC
11−1
A
(i|x, y)) + x
2i
y
2
AC
11−1
A−{i}
(x, y),
which implies that
AC
11−1
A
(i|x, y)=
x
i
y
1+x
i
y
AC
11−1
A
(x, y)+
x
2i
y
2
1+x
i
y
AC
11−1
A−{i}
(x, y).
Summing over i =1, 2,...,d,wegetthat
AC
11−1
A
(x, y)=1+
d
i=1
x
i
y
1+x
i
y
AC
11−1
A
(x, y)+
d
i=1
x
2i
y
2
1+x
i
y
AC
11−1
A−{i}
(x, y),
which is equivalent to
AC
11–1
A
(x, y)=
1+
d
i=1
x
2i
y
2
1+x
i
y
AC
11−1
A−{i}
(x, y)
1 −
d
i=1
x
i
y
1+x
i
y
, (5.6)
as claimed. 2
Example 5.40 The generating function for the pattern 11–1 is lengthy to
compute. For example, if n =15, we would need all the generating functions
AC
11–1
B
(x, y),whereB is a proper subset of [15], of which there are 2
15
−
1 = 32767. This is not very efficient, as each of these generating functions
takes several steps to compute. Instead, we may obtain the number of 11–1-
avoiding compositions of n by direct enumeration using a modification of the
Mathematica code given in Example 5.14. The values for n =0, 1,...,15 are
1, 1, 2, 3, 7, 12, 22, 40, 73, 136, 243, 433, 790, 1413, 2527 and 4516.
© 2010 by Taylor and Francis Group, LLC
Avoidance of Nonsubword Patterns in Compositions 159
We now give results for the patterns 11–2 and 22–1. Note the similarity of
the two generating functions, which stems from the fact that the two patterns
are complementary.
Theorem 5.41 Let A =[d]. Then the generating functions for the number of
compositions of n with m parts in [d] that avoid 11–2 and 22–1, respectively,
are given by
AC
11−2
[d]
(x, y)=
d
j=1
1 −
j−1
i=1
x
i
y
1+x
i
y
1 − x
j
y −
j−1
i=1
x
i
y
1+x
i
y
and
AC
22−1
[d]
(x, y)=
d
j=1
1 −
d
i=j+1
x
i
y
1+x
i
y
1 − x
j
y −
d
i=j+1
x
i
y
1+x
i
y
.
Proof Looking at the compositions that start with i, we obtain that
AC
11−2
[d]
(i|x, y)=x
i
y +
j=i
AC
11−2
[d]
(ij|x, y)+AC
11−2
[d]
(ii|x, y)
= x
i
y(AC
11−2
[d]
(x, y) − AC
11−2
[d]
(i|x, y)) + x
2i
y
2
AC
11−2
[i]
(x, y),
which implies that
AC
11−2
[d]
(i|x, y)=
x
i
y
1+x
i
y
AC
11−2
[d]
(x, y)+
x
2i
y
2
1+x
i
y
AC
11−2
[i]
(x, y).
Summing over i =1, 2,...,d and taking into consideration the empty compo-
sition, we obtain that
AC
11−2
[d]
(x, y)=1+
d
i=1
x
i
y
1+x
i
y
AC
11−2
[d]
(x, y)+
d
i=1
x
2i
y
2
1+x
i
y
AC
11−2
[i]
(x, y)
.
To create a recursion, we look at the difference AC
11−2
[d]
(x, y) −AC
11−2
[d−1]
(x, y).
Using AC
[d]
as a shorthand for AC
11−2
[d]
(x, y), we obtain
AC
[d]
− AC
[d−1]
=
d
i=1
x
i
y
1+x
i
y
AC
[d]
−
d−1
i=1
x
i
y
1+x
i
y
AC
[d−1]
+
x
2d
y
2
1+x
d
y
AC
[d]
,
which (after some algebraic manipulation) leads to
AC
11−2
[d]
(x, y)=
1 −
d−1
i=1
x
i
y
1+x
i
y
1 − x
d
y −
d−1
i=1
x
i
y
1+x
i
y
AC
11−2
[d−1]
(x, y)
© 2010 by Taylor and Francis Group, LLC
160 Combinatorics of Compositions and Words
for all d ≥ 1. Using the above recurrence relation d times together with the
initial condition AC
11−2
∅
(x, y) = 1, we get the result for AC
11−2
[d]
(x, y).
We now derive the result for the generating function for the 22–1-avoiding
compositions. The proof starts in the same way as the one for the 11–2-
avoiding compositions and we obtain that
AC
22−1
[d]
(i|x, y)=
x
i
y
1+x
i
y
AC
22−1
[d]
(x, y)+
x
2i
y
2
1+x
i
y
AC
22−1
[i,d]
(x, y). (5.7)
Unfortunately, the second summand in (5.7) now depends on both i and d and
will not cancel out when taking the difference AC
22−1
[d]
(x, y) − AC
22−1
[d−1]
(x, y).
Instead, we must first “normalize” this term so that it will once more cancel
out. Note that we can map any composition of n with m parts in {i,...,d} to
a composition of n
= n−m(i−1) with m parts in [d+1−i] by replacing σ
j
by
σ
j
−(i −1). In terms of generating functions, this means that AC
τ
[i,d]
(x, y)=
AC
τ
[d+1−i]
(x, x
i−1
y) for any pattern τ (using the definition of the generating
function). Replacing y by y/x
i−1
in (5.7) yields
AC
22−1
[d]
%
i|x,
y
x
i−1
&
=
xy
1+xy
AC
22−1
[d]
%
x,
y
x
i−1
&
+
x
2
y
2
1+xy
AC
22−1
[d+1−i]
(x, y).
Therefore,
AC
22−1
[d]
%
i|x,
y
x
i−1
&
− AC
22−1
[d−1]
%
i − 1|x,
y
x
i−2
&
=
xy
1+xy
AC
22−1
[d]
%
x,
y
x
i−1
&
−
xy
1+xy
AC
22−1
[d−1]
%
x,
y
x
i−2
&
.
Replacing y by x
i−1
y we obtain
AC
22−1
[d]
(i|x, y) −AC
22−1
[d−1]
(i − 1|x, xy)
=
x
i
y
1+x
i
y
AC
22−1
[d]
(x, y) −
x
i
y
1+x
i
y
AC
22−1
[d−1]
(x, xy).
Summing over i =2, 3,...,dand using that AC
22−1
[d]
(1|x, y)=xyAC
22−1
[d]
(x, y)
we get (after doing some algebra) that
1 − xy −
d
i=2
x
i
y
1+x
i
y
AC
22−1
[d]
(x, y)
=
1 −
d
i=2
x
i
y
1+x
i
y
AC
22−1
[d−1]
(x, xy).
Using the above recurrence relation d times together with the initial condition
AC
22−1
∅
(x, y) = 1 yields the desired result. 2
© 2010 by Taylor and Francis Group, LLC

Avoidance of Nonsubword Patterns in Compositions 161
Example 5.42 By taking the limit as d →∞and setting y =1in Theorem
5.41 we get that the generating functions for the number of compositions of n
that avoid the generalized patterns 11–2 and 22–1, respectively, are given by
AC
11–2
N
(x, 1) =
∞
j=1
1 −
j−1
i=1
x
i
1+x
i
1 − x
j
−
j−1
i=1
x
i
1+x
i
and
AC
22–1
N
(x, 1) =
∞
j=1
1 −
d
i=j+1
x
i
1+x
i
1 − x
j
−
∞
i=j+1
x
i
1+x
i
.
We use Mathematica or Maple to obtain the sequence [x
n
]AC
11–2
N
(x, 1) for
n =0to n =20as 1, 1, 2, 4, 7, 13, 24, 43, 77, 139, 248, 441, 786, 1394, 2469,
4374, 7730, 13649, 24093, 42478,and74847. The corresponding sequence for
22–1 is given by 1, 1, 2, 4, 8, 15, 30, 58, 112, 217, 420, 811, 1565, 3021, 5823,
11227, 21636, 41684, 80297, 154650,and297816.
Finally, we look at the generating functions for the remaining two classes.
For the patterns 12–2 ∼ 21–2 we obtain a very nice result that connects
pa
ttern avoidance in compositions to permutations.
Theorem 5.43 The generating function for the number of 12–2-avoiding
compositions of n with m parts in [d] is given by
AC
12–2
[d]
(x, y)=
B⊆[d]
κ∈S(B)
|B|
j=1
x
κ
j
y
(1 − x
κ
j
y)
|{i|κ
j
<κ
i
and i<j}|+1
,
where S(B) is the set of permutations of B.
Proof Let B ⊆ [d]andκ be fixed, where κ ∈S(B). Using Lemmas 5.31,
5.32, and 5.34 we obtain that the generating function for the number of com-
positions of n with m parts in AT
B
κ
(12–2) is given by
|B|
j=1
x
κ
j
y
(1 − x
κ
j
y)
|{i|κ
j
<κ
i
and i<j}|+1
.
The numerator of each term in the product accounts for the critical part,
while the denominator results from the product of the generating functions of
© 2010 by Taylor and Francis Group, LLC

162 Combinatorics of Compositions and Words
the |{i|κ
j
<κ
i
and i<j}| + 1 (potentially empty) b
j
-blocks. Now summing
over all the permutations κ of B, and over all subsets B of [d] we obtain that
AC
12–2
[d]
(x, y)=
B⊆[d]
κ∈S(B)
|B|
j=1
x
κ
j
y
(1 − x
κ
j
y)
|{i|κ
j
<κ
i
and i<j}|+1
,
as claimed. 2
Note that this proof, and therefore the result given in Theorem 5.43, can
be easily generalized to any ordered set A = {a
1
,a
2
,...,a
d
}⊂N.
Example 5.44 Even though Theorem 5.43 provides an explicit formula for
the generating function, it is not a formula that can be efficiently implemented
as a program. We have obtained the values for the number of 12–2-avoiding
compositions via direct enumeration using Mathematica or Maple for n =
0, 1,...,15 as 1, 1, 2, 4, 8, 15, 29, 55, 104, 194, 359, 660, 1208, 2200, 3982,
and 7166.
The last Wilf-equivalence class consists of the patterns 12–1 and 21–1. We
obtained this equivalence by applying the complement operation to the equiv-
alence 21–2 ∼ 12–2. Past experience with complementary patterns (see for
example Theorem 5.41) suggests that the generating functions of the comple-
mentary patterns are of very similar structure, but this is not the case. So
far, we have only been able to obtain the recursion for the generating func-
tion for the pattern 12–1 given in Theorem 5.46, not an explicit formula as
in Theorem 5.43. To find an explicit expression, especially one that involves
permutations, remains an open question (see Research Direction 5.1). We
make use of Lemma 5.45 to derive the generating function for the number of
12–1-avoiding compositions.
Lemma 5.45 The solution of the system of equations x
i
= β
i
+ α
i
i
j=1
x
j
,
i =1, 2,...,d is given by
x
i
=
β
i
1 − α
i
+ α
i
i−1
j=1
β
j
i
k=j
(1 − α
k
)
,i=1, 2,...,d.
Proof The linear system of equations can be presented as
(I − V
d
)(x
1
,...,x
d
)
T
=(β
1
,...,β
d
)
T
,
where V
d
=(v
ij
)
1≤i,j≤d
with v
ij
= α
i
if j ≤ i, and 0 otherwise. By Cramer’s
Rule, x
i
=
det(U
(i)
d
)
det(I−V
d
)
,whereU
(i)
d
is the matrix obtained from I − V
d
by
replacing its i-th column by the column (β
1
,...,β
d
)
T
.ThematrixI − V
d
is
lower triangular, therefore det(I−V
d
)=
d
j=1
(1−α
j
). Since U
(i)
d
is a special
© 2010 by Taylor and Francis Group, LLC

Avoidance of Nonsubword Patterns in Compositions 163
type of block matrix, we obtain that det(U
(i)
d
)=
d
j=i+1
(1−α
j
)det(U
(i)
i
)(see
Theorem B.15). Using routine techniques from linear algebra (see Exercise
5.4), one can show that
det(U
(i)
i
)=β
i
i−1
j=1
(1 − α
j
)+α
i
i−1
j=1
β
j
j−1
k=1
(1 − α
k
).
Hence,
x
i
=
det(U
(i)
i
)
i
j=1
(1 − α
j
)
=
β
i
1 − α
i
+
α
i
i
j=1
(1 − α
j
)
i−1
j=1
β
j
j−1
k=1
(1 − α
k
),
which after simplification completes the proof. 2
Using this lemma, we can prove a result for the generating function of the
patterns in the remaining Wilf-equivalence class.
Theorem 5.46 For A =[d] ⊆ N and τ =12–1,
AC
τ
A
(x, y)=1+
d
i=1
x
i
y
1 − x
i
y
⎛
⎝
1+
d
j=i+1
AC
τ
A−{i}
(j|x, y)
⎞
⎠
+
d
i=2
i−1
j=1
x
i+j
y
2
i
k=j
(1 − x
k
y)
⎛
⎝
1+
d
k=j+1
AC
τ
A−{j}
(k|x, y)
⎞
⎠
,
where
AC
τ
A
(i|x, y)=x
i
y + x
i
y
i
j=1
AC
τ
A
(j|x, y)+x
i
y
d
j=i+1
AC
τ
A−{i}
(j|x, y).
Proof Using arguments similar to those in the proofs of the other generating
functions, we get that AC
τ
A
(i|x, y)satisfies
AC
τ
A
(i|x, y)=x
i
y + x
i
y
i
j=1
AC
τ
A
(j|x, y)+x
i
y
d
j=i+1
AC
τ
A−{i}
(j|x, y).
Applying Lemma 5.45 with α
i
= x
i
y and
β
i
= x
i
y(1 +
d
j=i+1
AC
τ
A−{i}
(j|x, y))
© 2010 by Taylor and Francis Group, LLC

164 Combinatorics of Compositions and Words
gives
AC
τ
A
(i|x, y)=
x
i
y
1 − x
i
y
%
1+
d
j=i+1
AC
τ
A−{i}
(j|x, y)
&
+
i−1
j=1
x
i+j
y
2
i
k=j
(1 − x
k
y)
%
1+
d
k=j+1
AC
τ
A−{j}
(k|x, y)
&
for all i =1, 2,...,d.TheresultforAC
τ
A
(x, y) then follows from (5.1). 2
Note that Theorem 5.46 can be easily generalized to A = {a
i
,a
2
,...,a
d
}
by replacing i by a
i
.
Example 5.47 The recursive formula for the generating function is not use-
ful for computing the number of compositions avoiding 12–1.Weobtained
the sequence of values by direct enumeration (using Mathematica or Maple)
as 1, 1, 2, 4, 7, 13, 23, 40, 68, 117, 195, 323, 531, 863, 1394,and2234 for
n =0, 1,...,15.
This completes the classification of all generalized patterns of length three.
We now turn our attention to the last type of pattern that we will consider.
5.4 Partially ordered patterns in compositions
Most papers on partially ordered patterns consider avoidance of these pat-
terns, but there are also some enumeration results. We start by presenting
results on the number of occurrences of a given pattern in all compositions
of n [111], and then give results on avoidance of partially ordered patterns
in compositions of n [88]. Note that in [108] and [111], the patterns under
study are called POGPs (partially ordered generalized patterns) and SPOPs
(segmented partially ordered patterns), respectively. Segmented patterns are
the same as subword patterns, so we refer to them as such, consistent with
the rest of the book. However, what is common to POGPs and SPOPs is that
they are defined on a partially ordered alphabet, and so we refer to them as
partially ordered patterns or POPs.
Definition 5.48 A partially ordered generalized pattern ξ is a word (in re-
duced form) consisting of letters from a partially ordered alphabet T (see Defi-
nition 7.44). If letters a and b are incomparable in a POP ξ, then the relative
size of the letters corresponding to a and b in a composition σ is unimpor-
tant in an occurrence of ξ in the composition σ. Letters shown with the same
number of primes are comparable to each other (for example, 1
and 3
are
comparable), while letters shown without primes are comparable to all letters
© 2010 by Taylor and Francis Group, LLC
