Heubach S., Mansour T. Combinatorics of Compositions and Words

Подождите немного. Документ загружается.

Avoidance of Nonsubword Patterns in Compositions 135

where the Mathematica function Apply in conjunction with the function Plus

adds the coeﬃcients for a given n. Note that the Maple function mtaylor gives

the Taylor series for a function of several variables. The sequence produced

by these commands is 1, 1, 1, 3, 3, 5, 11, 13, 19, 27, 57, 65, 101, 133, 193,

351, 435, 617, 851, 1177,and1555 for n =0, 1,...,20.

5.2.1 Subsequence patterns of length three in S

We will now consider avoidance of subsequence patterns of length three.

The ﬁrst result on subsequence patterns in compositions was given by Savage

and Wilf [176]. For the six permutation patterns of length three, namely 123,

132, 213, 231, 312 and 321, the reversal map immediately gives the following

Wilf-equivalences:

123 ∼ 321, 132 ∼ 231 and 213 ∼ 312.

However, Savage and Wilf showed a much stronger result, which we give in a

slightly modiﬁed form that is useful for computations of the coeﬃcients. The

result given in [176] does not include enumeration according to parts, and

gives the generating function for A = N (as opposed to A =[n]).

Theorem 5.7 [176] The number of compositions of n with parts in N that

avoid a given 3-letter permutation pattern τ is independent of τ, that is, 123 ∼

132 ∼ 213. The generating function is given by

[n]

(x, y)=



i=1

i(n−1)

(1 − x

n−2



j=1,j=i

− x

)(1 − x

y − x

The proof of this result uses the complement map on compositions.

Deﬁnition 5.8 Let A =[d]. For any composition σ = σ

···σ

of n with

m parts in A, we deﬁne its complement c(σ)=c

(σ) with respect to A as

the composition where σ

is replaced by d +1− σ

Note that c(σ) is a composition of





i=1

(d +1− σ

)=m(d +1)− n

with m parts in A.

Proof We paraphrase the proof given in [176] using our notation. At the

core of the proof are results on the enumeration of permutations of a multiset

that avoid a given pattern. This enumeration was accomplished for the pat-

tern 132 by Albert et al. in [6, Lemma 1]. To utilize these results, we need

136 Combinatorics of Compositions and Words

to connect compositions with multisets. For a vector

→

m =(m

,...,m

)

of positive integers, we deﬁne M(

→

m) to be the multiset that contains exactly

copies of the part i,fori =1, 2,...,k. Then the permutations of the

multiset give exactly all the compositions that are made up from the parts

of the multiset. Now let f(

→

m,τ) be the number of permutations of the mul-

tiset M(

→

m) that avoid the pattern τ.In[6]itwasshownthatforevery

→

m,123) = f (

→

m,132), and that f(

→

m,132) is a symmetric function of

→

The ﬁrst assertion gives that 123 ∼ 132, since we can deﬁne an equivalence

relation on the set of compositions by declaring two compositions equivalent

if they have the same multiset of parts, and the Wilf-equivalence holds on

each of the equivalence classes, therefore overall. All that is missing is to

show that 132 ∼ 312. First observe that f(

→

m,τ)=f(R(

→

m),c(τ)), since the

reversal of

→

m replaces the number of occurrences of the letter i by the number

of occurrences of the letter k +1− i, which matches the substitution of let-

ters in the complement operation. In particular, f (

→

m,132) = f(R(

→

m), 312)

Fina

lly, we use that the counting function f(

→

m,132) is symmetric in the m

therefore f(

→

m,132) = f(R(

→

m), 132) = f(R(R(

→

m)), 312) = f(

→

m,312), which

shows that the number of compositions avoiding any 3-letter permutation pat-

tern τ is independent of τ. The generating function follows with appropriate

modiﬁcations for incorporating the number of parts from the results given in

[6] and Equation 2 in [176]. 2

An alternative proof of this result based on a generalization of the Simion-

Schmidt construction [179] was given by Myers [157].

Example 5.9 We compute the sequence for the number of compositions that

avoid any one of the permutation patterns of length three using Mathematica

or Maple for n =20. Here are the respective codes:

f[x_] := Sum[x^(19 i) (1-x^i)^18/

(Product[(x^i-x^j) (1-x^i-x^j), {j,1, i-1}]

Product[(x^i-x^j) (1-x^i-x^j), {j, i+1,20}]), {i,1,20}]

CoefficientList[Series[f[x], {x, 0, 20}],x]

and

f:=taylor(sum(x^(i*19)*(1-x^i)^(18)/

product((x^i-x^j)*(1-x^i-x^j),’j’=1..i-1)/

product((x^i-x^j)*(1-x^i-x^j),’j’=i+1..k),’i’=1..20)

,x=0,21);

The resulting sequence is given by 1, 1, 2, 4, 8, 16, 31, 60, 114, 214, 398,

732, 1334, 2410, 4321, 7688, 13590, 23869, 41686, 72405 and 125144 for

n =0, 1,...,20.

Avoidance of Nonsubword Patterns in Compositions 137

5.2.2 Three-letter subsequence patterns with repetitions

What remains to be studied are the seven patterns of length three with

repetitions, namely 111, 112 ∼ 211, 121, 221 ∼ 122, and 212. Heubach and

Mansour [91] suggested algorithms showing that

112 ∼ 121 and 221 ∼ 212

based on the algorithm given by Burstein and Mansour [33] for proving that

the number of words avoiding 112 and 121, respectively, is the same. However,

the authors and Augustine found an error in this algorithm; the correction

appears as additional pages for the original paper [33, Page 15]. Here we

present the results using the corrected algorithm.

Theorem 5.10 For any ordered set A = {a

,...,a

}⊆N, 112 ∼ 121 and

221 ∼ 212.

Proof We ﬁrst analyze the structure of the compositions avoiding 121 and

112, respectively. If σ ∈AC

(121), then it cannot contain parts other than a

between any two occurrences of a

, which means that if σ contains the part a

more than once, then all such a

have to be consecutive. Deletion of all parts

from σ results in a composition σ



which avoids 121, and all occurrences

of a

in σ



, if any, have to be consecutive. In general, step-wise deletion of

all parts a

through a

leaves a (possibly empty) composition ˜σ with parts in

j+1

,...,a

} in which all parts a

j+1

, if any, occur consecutively.

On the other hand, if σ ∈AC

(112), then only the leftmost a

of σ can occur

before any larger part. The remaining parts a

must occur at the end of σ.In

fact, just as in the previous case, step-wise deletion of all parts a

through a

leaves a (possibly empty) composition ¯σ with parts in {a

j+1

,...,a

} in which

all occurrences of a

j+1

, except possibly the leftmost one, occur at the end of

¯σ.

We will call all occurrences of a part a

occurring after the the leftmost

and before any a

with k>jexcess a

. We deﬁne an excess a

-block as

follows: If the part a

occurs at least twice in σ, then an excess a

-block is the

longest sequence of consecutive parts σ



···σ

+v

, v ≥ 0 starting at the second

from the left (at position ) satisfying these conditions:

(1) σ

+r

≤ a

for all 0 ≤ r ≤ v.

(2) if σ

+r

= a

for some 0 ≤ r ≤ v,thenσ

+r

is not an excess a

,that

is, a

occurs for the ﬁrst time in σ.

We now describe the algorithm for the bijection ρ : AC

(121) →AC

(112).

Given a composition σ ∈AC

(121), we deﬁne σ

(0)

= σ and apply the fol-

lowing transformation of d steps. Let σ

(j−1)

be the composition that results

from applying the transformation step j −1times,whereσ

(j)

is obtained from

138 Combinatorics of Compositions and Words

(j−1)

by cutting out the excess a

-block and inserting it immediately before

any excess a

-blocks, where i<j,orattheendofσ

(j−1)

if there are no ex-

cess a

-blocks. Then ρ(σ)=σ

(d)

. Clearly, σ

(d)

∈AC

(112) at the end of the

algorithm, and the deﬁnition of the excess a

-blocks insures uniqueness. Here

is an example illustrating the algorithm, where σ = 3311132244 ∈AC

[4]

(121)

and a

= j for j =1, 2, 3, 4. For emphasis, the excess j-blocks have been

underlined in the transformation of 3311132244:

33111

32244 → 3313224411 → 3313244211 → 3443132211 → 3443132211.

The inverse map consists of moving each excess a

-block to the position

immediately after the leftmost a

,forj = d, d − 1,...,1. We have therefore

shown that the patterns 121 and 112 are Wilf-equivalent on compositions.

For A =[d], the second Wilf-equivalence, 221 ∼ 212, is easily proved by

using the complement operation on the equivalence 112 ∼ 121. Let σ ∈

n,m

(221) be such that the part i occurs in σ exactly r

times. Then c(σ) ∈



(112), and the part i occurs exactly r

d+1−i

times. Since c is one-to-one

and 112 ∼ 121, this implies the Wilf-equivalence of the patterns 221 and 212.

For general A, we cannot use the complement map; instead, one can modify

the bijection ρ given for the patterns 112 and 121 to show that 221 ∼ 212. 2

Thus we only need to obtain the generating functions for the number of

compositions that avoid the patterns 111, 112 and 221, respectively. For

avoidance of the pattern 111, it is most useful to state the exponential gener-

ating function.

Theorem 5.11 For any ordered set A = {a

,...,a

}⊆N, the exponential

generating function for the number of compositions of n with m parts in A

that avoid the pattern 111 is given by



m≥0

111

(m; x)



a∈A

(1 + x

y +

Proof Let σ ∈AC

n,m

(111). Thus, the number of occurrences of the letter a

in σ is 0, 1 or 2, and the number of such compositions is given by AC

111

(m; n),

mAC

111

(m −1; n −a

)and





111

(m −2; n −2a

), respectively. Adding

the three cases, multiplying by

and summing over all n, m ≥ 0we

get that



m≥0

111

(m; x)



1+x

y +





m≥0

111

(m; x)

Since



m≥0

111

}

(m; x)

=1+x

y +

, we get the desired result

by induction on d. 2

Avoidance of Nonsubword Patterns in Compositions 139

Example 5.12 We use Theorem 5.11 to obtain the sequence of values for

the number of compositions of n avoiding the subsequence pattern 111 by set-

ting A =[n]. Since we have an exponential generating function, we have to

be careful when using Mathematica or Maple. First we create the series in

terms of x and y,thenextractthecoeﬃcientsofx

, multiply those by m!,

and then sum over all values of m for a given n.TheMathematica code to

accomplish this for n ≥ 1 is given below.

Apply[Plus,Table[Coefficient[Series[

Product[1+x^i*y +x^(2i)*y^2/2, {i, 1, 20}],

{x, 0, 20}, {y, 0, 20}],

x^n*y^m ]*m!, {n, 1, 20}, {m, 1, 20}], 1]

The corresponding Maple code is given by

taylor(sum(coeff(simplify(taylor(

product(1+x^i*y+x^(2*i)*y^2/2,’i’=1..20),y,21)

),y,j)*j!,’j’=0..20),x,21)

The resulting sequence of values for n =0, 1,...,20 is given by 1, 1, 2, 3, 7,

11, 21, 34, 59, 114, 178, 284, 522, 823, 1352, 2133, 3739, 5807, 9063, 14074,

and 23639.

For the remaining two patterns we are able to obtain an explicit formula

involving partial derivatives. This formula is rather complicated and not

very useful for actual computations when n is larger than 11. Finding “nice”

explicit expressions for AC

112

(x, y)andAC

221

(x, y) remains an open question

(see Research Direction 5.1). Note the similarity in structure for the two

patterns 112 and 221, which comes from the fact that they are complementary.

Theorem 5.13 Let b

1 − x

, c

and A = {a

,...,a

Then

112

(x, y)

= b

∂

∂y



−c

∂

∂y



···

∂

∂y



d−1

−c

d−2

∂

∂y



−c

d−1

1 − x



···



and

221

(x, y)

= b

∂

∂y



d−1

−c

∂

∂y



···

∂

∂y



−c

∂

∂y



−c

1 − x



···



140 Combinatorics of Compositions and Words

Proof We start by deriving a recursion for AC

112

(x, y). Let H

112

(x, y)be

the generating function for compositions σ ∈AC

n,m

(112) which contain at

least one part a

.Thus,

112

(x, y)=AC

112

(x, y) − AC

112

(x, y). (5.2)

On the other hand, each such σ either ends in a

or not. If σ ends in a

,then

deletion of this a

results in a composition ˜σ ∈AC

n−a

,m−1

(112), since the

at the right end of σ cannot be part of an occurrence of the pattern 112.

If σ does not end in a

,thenσ contains exactly one a

. Deletion of the single

produces a composition ˜σ ∈AC

n−a

,m−1

(112), and there are exactly m−1

such compositions. Thus, we have an alternative expression for H

112

(x, y):

112

(x, y)

= x

yAC

112

(x, y)+



n≥a

,m≥1

(m − 1)AC

112

(m − 1; n − a

= x

yAC

112

(x, y)+x

∂

∂y

112

(x, y). (5.3)

Combining (5.2) and (5.3) results in

(1 − x

y)AC

112

(x, y)=AC

112

(x, y)+x

∂

∂y

112

(x, y).

If we multiply this recurrence by e

−c

/(x

), then the right-hand side be-

comes a single partial derivative, and we obtain that

−c

112

(x, y)=

∂

∂y

−c

112

(x, y)

which is equivalent to

112

(x, y)=b

∂

∂y

−c

112

(x, y)

Iterating this recurrence results in the explicit formula for AC

112

(x, y). The

result for AC

221

(x, y) follows by replacing a

with a

and

with A

d−1

the derivation for AC

112

(x, y). 2

Example 5.14 The explicit formulas for the generating functions for the pat-

terns 112 and 221 are not practical for obtaining the sequence values as com-

putational eﬀort increases rapidly with n. Using the explicit formula in Maple

or Mathematica we obtain results only up to n =11in a reasonable amount of

time. An alternative approach consists of creating the list of compositions of

n in Mathematica, then using pattern matching to determine which of those

contain the respective pattern. Subtracting the number of compositions that

Avoidance of Nonsubword Patterns in Compositions 141

contain a given pattern from the total number of compositions of n gives the

desired sequence of values. This approach allows us to get the values for the

number of compositions that avoid either 112 or 221 for n ≤ 15 before the

computational eﬀort becomes too large. Below we give the Mathematica code

for the pattern matching approach for 112.

comps[n_]:=Flatten[Map[Permutations,IntegerPartitions[n]],1];

Table[2^(k - 1) - Length[Position[comps[k],

{___, x_, ___, x_, ___, y_, ___} /; x<y]], {k,1,15}]

The sequence of values [x

]AC

112

(x, y) is given by 1, 1, 2, 4, 7, 13, 23,

40, 67, 115, 190, 311, 505, 807, 1285,and2031 for n =0, 1,...,15;the

corresponding sequence for the pattern 221 is given by 1, 1, 2, 4, 8, 15, 29,

55, 103, 190, 347, 630, 1134, 2028, 3585,and6291.

Since both Mathematica and Maple reach their limits rather quickly, we

provide C++ and Java codes for ﬁnding the sequence of values for the number

of compositions of n with parts in N that avoid a subsequence pattern τ of

length less than or equal to seven for any n. These programs are given in

Appendix G. For results on avoiding more than one pattern with repetitions

we refer the reader to [91] and Exercise 5.5.

5.2.3 Wilf-classes for longer subsequence patterns

In the previous two subsections we completely classiﬁed the patterns of

length three according to Wilf-equivalence. We summarize these results in

Table 5.1 for the nontrivial Wilf-equivalence classes, that is, those that do not

just contain a pattern and its reverse. For patterns of length three, the only

trivial class consists of the pattern 111.

TABLE 5.1: Wilf-equivalence classes for patterns of length three

123∼132∼213 112∼121 122∼212

For longer patterns, Mansour and Jel´ınek [105, 104] provided classiﬁca-

tion results for patterns according to strong equivalence which implies Wilf-

equivalence (see Deﬁnition 6.10). Utilizing the C++ code given in Appendix

G together with their structure results (Propositions 6.18 and 6.19 and The-

orem 6.20), Mansour and Jel´ınek gave a complete classiﬁcation for patterns

of lengths four and ﬁve for compositions. Tables 5.2 and 5.3 list the lexico-

graphically minimal patterns for the nontrivial Wilf-equivalence classes.

More detailed tables where the equivalence classes are listed together with

values of AC

(n) for selected values of n appear in Appendix G. The values

142 Combinatorics of Compositions and Words

TABLE 5.2: Wilf-equivalence classes for patterns of length four

1234∼1243∼1432∼2134∼2143∼3214 1112∼1121 1123∼1132

1223∼1232∼1322∼2123∼2132∼2213 1233∼2133 1222∼2122

TABLE 5.3: Wilf-equivalence classes for patterns of length ﬁve

12223∼12232∼12322∼13222∼21223∼21232 12134∼12143

∼21322∼22123∼22132∼22213 12443∼21443

12345∼12354∼12543∼15432∼21345∼21354 12434∼21434

∼21543∼32145∼32154∼43215 12534∼21534

12234∼12243∼21234∼21243∼22134∼22143 11123∼11132

12334∼12343∼12433∼21334∼21343∼21433 12333∼21333

11112∼11121∼11211 12435∼21435

11223∼11232∼11322 12453∼21453

12222∼21222∼22122 13245∼13254

11234∼11243∼11432 23145∼23154

12233∼21233∼22133 21134∼21143

12344∼21344∼32144 31245∼31254

shown are those that take relatively long to compute and which clearly show

that the classes are indeed diﬀerent. Sequence values for smaller n can be

quickly computed using the C++ code given in Appendix G. Finding explicit

or recursive expressions for the respective generating functions is an open

problem (see Research Direction 5.2).

5.3 Generalized patterns and compositions

In Chapter 4 and in Section 5.2 we discussed enumeration and avoidance

of subword patterns and subsequence patterns. These two types of patterns

are special cases of the so-called generalized patterns, which were introduced

by Babson and Steingr´ımsson [11] in the context of permutations to study

Mahonian statistics.

Deﬁnition 5.15 A generalized pattern of length k isawordconsistingofk

letters in which two adjacent letters may or may not be separated by a dash.

The absence of a dash between two adjacent letters in the pattern indicates that

the corresponding letters in the permutation, word, composition, or partition

must be adjacent. If the pattern τ is of the form τ = τ

(1)

–τ

(2)

– ···–τ

()

where

the τ

(i)

are all subword patterns of lengths j

,thenτ is of type (j

,...,j



The reversal map for a generalized pattern generalizes from Deﬁnition 4.22

in the obvious manner, namely reversing the parts of the pattern, and keeping

intact any adjacency requirements.

Avoidance of Nonsubword Patterns in Compositions 143

Note that a subword pattern is a generalized pattern that has no dashes,

and a subsequence pattern is a generalized pattern that has dashes between

all pairs of adjacent letters.

Deﬁnition 5.16 Asequence(permutation, word, composition or partition)

σ contains a generalized pattern τ of length k if τ equals the reduced form of

any k-term subsequence of σ that follows the adjacency requirements given by

τ. Otherwise we say that σ avoids the generalized pattern τ or is τ-avoiding.

Example 5.17 Let τ =13–2–1.Thenτ is of type (2, 1, 1),sinceτ

(1)

=13,

(2)

=2,andτ

(3)

=1,andR(τ )=1–2–31.Furthermore,τ occurs in σ if

there is a subsequence σ

i+1



with i +1 <j<and σ

= σ



<σ

i+1

Thus, the composition 253452 contains two occurrences of 13–2–1,namely

= 2532 and σ

= 2542.

In this section we study generalized patterns of length three for composi-

tions. The only 3-letter generalized patterns that we have not yet discussed

are those with one dash (or one adjacent pair of letters), that is, the patterns

of type (2, 1). Note that if τ is of type (2, 1), then R(τ)isoftype(1, 2);

thus, for the purpose of Wilf-equivalence, we only need to look at type (2, 1)

patterns. These patterns were studied by Claesson [55] for permutations and

Burstein and Mansour [33] for words.

We will ﬁrst consider type (2, 1) permutation patterns, and then type (2, 1)

patterns that have repeated letters.

5.3.1 Permutation patterns of type (2,1)

There are six permutation patterns of type (2, 1), namely 12–3, 13–2, 21–3,

23–1, 31–2 and 32–1. These patterns fall into three separate equivalence

classes. Not surprisingly, the classes split up according to the last part of the

pattern, that is, the two patterns that have the same last part form a Wilf

equivalence class. One might expect that a bijection that reverses the parts

of the composition corresponding to the adjacent pair in the pattern would

do the trick of showing Wilf-equivalence. This is indeed the case for two of

the equivalence classes, but does not work for showing that 13–2 ∼ 31–2. We

will start with the easy cases.

Theorem 5.18 For any ordered set A = {a

,...}⊆N, 12–3 ∼ 21–3 and

23–1 ∼ 32–1.

Proof We show that 12–3 ∼ 21–3 by giving a bijection φ between the sets

of compositions of n with m parts in A avoiding the respective patterns. Let

σ ∈AC

n,m

(12–3) and assume that σ has maximal part a

which occurs s

times. Thus, σ can be decomposed as

σ = σ

(1)

(2)

···a

(s)

(s+1)

144 Combinatorics of Compositions and Words

where each σ

(i)

is a nonincreasing composition with parts in A

j−1

for i =

1,...,s,andσ

(s+1)

is a composition with parts in A

j−1

that avoids 12–3. We

deﬁne φ(σ) recursively as

φ(σ)=R(σ

(1)

R(σ

(2)

···a

R(σ

(s)

φ(σ

(s+1)

where R is the reversal map. Clearly, σ avoids 12–3 if and only if φ(σ)avoids

21–3, and σ and φ(σ)arebothinC

n,m

. Thus, 12–3 ∼ 21–3; the proof for

23–1 ∼ 32–1 follows with appropriate adjustments. 2

Now we deal with the harder equivalence.

Theorem 5.19 For any ordered set A = {a

,...,a

}⊆N, 13–2 ∼ 31–2.

Proof We deﬁne an algorithm that transforms σ ∈AC

n,m

(13–2) into σ



∈

n,m

(31–2) and vice versa, thereby giving a bijection between AC

n,m

(13–2)

and AC

n,m

(31–2). The basic idea is to move blocks of “1”s from one side of

the (single) “3” to the other, leaving the corresponding (single)“2” in place.

This process transforms a 13–2 pattern into a 31–2 pattern and vice versa.

We make this idea precise with the following deﬁnitions: An ascent in σ is

an integer σ

such that σ

<σ

i+1

for i ≥ 1. The ascent σ

is called active

if there is an integer σ

such that i +1<jand σ

<σ

i+1

,thatis,an

active ascent is the “1” in an occurrence of the pattern 13–2 of width j −i +1.

Note that an active ascent can be part of more than one occurrence of 13–2,

and that σ ∈AC

n,m

(13–2) cannot have an active ascent. For each occurrence

of a pattern 13–2 we deﬁne the associated ascent block to be the maximal

substring σ

k+1

···σ

such that σ



<σ

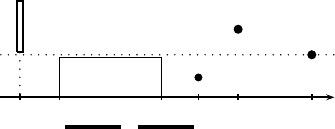
for  = k,k +1,...,i. Figure 5.1

visualizes the schematic structure of an ascent block.

k−1 k i−1 i i+1 j

≥ 2

index

-. /

ascent block

FIGURE 5.1: Structure of ascent block.

Similarly, a descent in a composition σ is an integer σ

such that σ

i−1

>σ

for i>1. The descent σ

is called active if there is an integer σ

such that