Helms L.L. Potential Theory
Подождите немного. Документ загружается.


338 9 Elliptic Operators
The following lemma is an immediate consequence of Theorem 8.4.5 and
Inequalities (9.5) and (9.6).
Lemma 9.3.1 If u ∈ C
2
(Ω),f ∈ H
(2)
α
(Ω; d),α ∈ (0, 1),andL
0
u = f on Ω,
then
|u; d|
2+α,Ω
≤ C(n, α, m, M)(u
0,Ω
+ |f ; d|
(2)
α,Ω
).
9.4 Schauder Interior Estimates
The following terminology regarding the operator L will be used. If there are
positive functions m and M on the open set Ω ⊂ R
n
such that
m|λ|
2
≤
n
i,j=1
a
ij
(x)λ
i
λ
j
≤ M |λ|
2
for all x ∈ Ω, λ ∈ R
n
, (9.9)
the operator L is said to be elliptic on Ω;ifm is a positive constant, L is said
to be strictly elliptic on Ω. Granted that the solution of the equation Lu =
f is bounded, a bound for the weighted norm |u; d|
2+α,Ω
can be obtained.
Such estimates are called Schauder interior estimates. All of the results
in this section can be found in [25].
Lemma 9.4.1 If α ∈ (0, 1),a + α ≥ 0,b + α ≥ 0,a + b + α ≥ 0,f ∈
H
(a)
α
(Ω; φ),g ∈ H
(b)
α
(Ω; φ),thenfg ∈ H
(a+b)
α
(Ω; φ) and
|fg; φ|
(a+b)
α,Ω
≤|f; φ|
(a)
α,Ω
|g; φ|
(b)
α,Ω
. (9.10)
Proof: By definition,
|fg; φ|
(a+b)
α,Ω
=sup
x∈Ω
φ
a+b
(x)|f(x)g(x)|
+sup
x,y∈Ω
φ
a+b+α
(x, y)
|f(x)g(x) − f (y)g(y)|
|x − y|
α
≤|f; φ|
(a)
0,Ω
|g; φ|
(b)
0,Ω
+sup
x,y∈Ω
φ
a+b+α
(x, y)
|f(x)||g(x) − g(y)| + |g(y)||f(x) − f(y)|
|x − y|
α
≤|f; φ|
(a)
0,Ω
|g; φ|
(b)
0,Ω
+[f; φ]
(a)
0,Ω
[g; φ]
(b)
α,Ω
+|g; φ|
(b)
0,Ω
[f; φ]
(a)
α,Ω
≤
|f; φ|
(a)
0,Ω
+[f; φ]
(a)
α,Ω
|g; φ|
(b)
0,Ω
+[g; φ]
(b)
α,Ω
= |f; φ|
(a)
α,Ω
|g; φ|
(b)
α,Ω
.
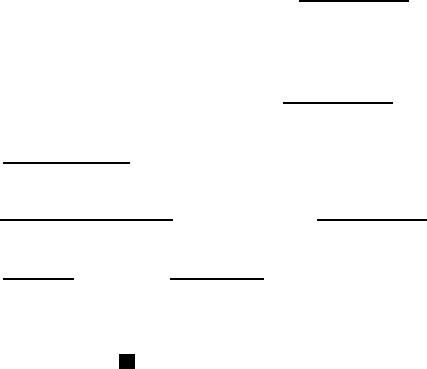
9.4 Schauder Interior Estimates 339
Lemma 9.4.2 If α ∈ (0, 1),g ∈ H
(2)
α
(Ω,d),μ ≤ 1/2,x
0
∈ Ω, δ = μd(x
0
),
and B = B
x
0
,δ
,then
|g; d
B
|
(2)
α,B
≤ 4μ
2
[g; d]
(2)
0,Ω
+8μ
2+α
[g; d]
(2)
α,Ω
≤ 8μ
2
|g; d|
(2)
α,Ω
. (9.11)
Proof: For x ∈ B, d
B
(x)=d(x, ∂B) <δand d(x) ≥ (1 − μ)d(x
0
)sothat
|g; d
B
|
(2)
α,B
=sup
x∈B
d
2
B
(x)|g(x)| +sup
x,y∈B
d
2+α
B
(x, y)
|g(x) − g(y)|
|x − y|
α
≤ δ
2
sup
x∈B
d
−2
(x)d
2
(x)|g(x)|
+ δ
2+α
sup
x,y∈B
d
−2−α
(x, y)d
2+α
(x, y)
|g(x) − g(y)|
|x − y|
α
≤
δ
2
(1 − μ)
2
d
2
(x
0
)
sup
x∈Ω
d
2
(x)|g(x)|
+
δ
2+α
(1 − μ)
2+α
d
2+α
(x
0
)
sup
x,y∈Ω
d
2+α
(x, y)
|g(x) − g(y)|
|x − y|
α
≤
μ
2
(1 − μ)
2
[g; d]
(2)
0,Ω
+
μ
2+α
(1 − μ)
2+α
[g; d]
(2)
α,Ω
≤ 4μ
2
[g; d]
(2)
0,Ω
+8μ
2+α
[g; d]
(2)
α,Ω
≤ 8μ
2
|g; d|
(2)
α,Ω
.
Lemma 9.4.3 Let Ω be a bounded open subset of R
n
and let L be an elliptic
operator on Ω satisfying
|a
ij
; d|
(0)
α,Ω
, |b
i
; d|
(1)
α,Ω
, |c; d|
(2)
α,Ω
≤ K, α ∈ (0, 1),i,j =1,...,n. (9.12)
If u ∈ H
2+α
(Ω; d),f ∈ H
(2)
α
(Ω; d),α ∈ (0, 1),andLu = f ,then
|u; d|
2+α,Ω
≤ C(u
0,Ω
+ |f ; d|
(2)
α,Ω
). (9.13)
where C = C(m, n, α, K).
Proof: By Inequality (7.10), it suffices to prove the result for [u; d]
2+α,Ω
.Let
x
0
,y
0
be two points of Ω with x
0
= y
0
and labeled so that d(x
0
) ≤ d(y
0
), let
μ ≤ 1/2 be a constant that will be further specified later, let δ = μd(x
0
), and
let B = B
x
0
,δ
. The equation Lu = f can be related to an elliptic operator
with constant coefficients by writing
n
i,j=1
a
ij
(x
0
)D
ij
u(x)=
n
i,j=1
(a
ij
(x
0
) − a
ij
(x))D
ij
u(x)
−
n
i=1
b
i
(x)D
i
u(x) − c(x)u(x)+f(x).
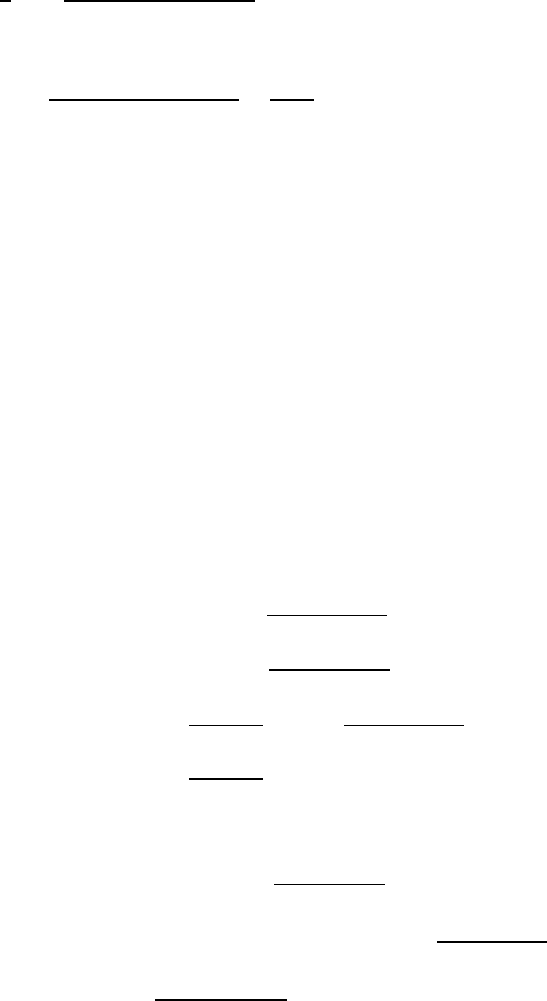
340 9 Elliptic Operators
Denote the left side of this equation by L
0
u and the right side by f
0
.Note
that for y
0
∈ B
x
0
,δ/2
,d(y
0
,∂B) ≥ δ/2 so that by Lemma 9.3.1,
δ
2
2+α
|D
ij
u(x
0
) − D
ij
u(y
0
)|
|x
0
− y
0
|
α
≤ C
u
0,B
+ |f
0
; d
B
|
(2)
α,B
(9.14)
where C = C(m, n, α, K). Since δ = μd(x
0
)=μd(x
0
,y
0
),
d
2+α
(x
0
,y
0
)
|D
ij
u(x
0
) − D
ij
u(y
0
)|
|x
0
− y
0
|
α
≤
1
μ
2+α
C
u
0,B
+ |f
0
; d
B
|
(2)
α,B
. (9.15)
Each of the terms on the right side of the inequality
|f
0
; d
B
|
(2)
α,B
≤
n
i,j=1
|(a
ij
(x
0
) − a
ij
)D
ij
u; d
B
|
(2)
α,B
+
n
i=1
|b
i
D
i
u; d
B
|
(2)
α,B
+ |cu; d
B
|
(2)
α,B
+ |f ; d
B
|
(2)
α,B
(9.16)
can be estimated as follows. The subscripts on a
ij
will be omitted temporarily.
Keep in mind that D
2
is a generic symbol for a second-order partial derivative.
By Inequalities (9.10) and (9.11),
|(a(x
0
) − a)D
2
u; d
B
|
(2)
α,B
≤|a(x
0
) − a; d
B
|
(0)
α,B
|D
2
u; d
B
|
(2)
α,B
≤|a(x
0
) − a; d
B
|
α,B
4μ
2
[D
2
u; d]
(2)
0,Ω
+8μ
2+α
[D
2
u; d]
(2)
α,Ω
≤|a(x
0
) − a; d
B
|
α,B
4μ
2
[u; d]
2+0,Ω
+8μ
2+α
[u; d]
2+α,Ω
.
Using the fact that (1 − μ)d(x
0
) ≤ d(x), (1 − μ)d(x
0
) ≤ min (d(x
0
),d(x)) =
d(x
0
,x)forx ∈ B,
|a(x
0
) − a(x)| = |x − x
0
|
α
|a(x
0
) − a(x)|
|x − x
0
|
α
≤ μ
α
d(x
0
)
α
|a(x
0
) − a(x)|
|x − x
0
|
α
≤
μ
α
(1 − μ)
α
d
α
(x
0
,x)
|a(x
0
) − a(x)|
|x − x
0
|
α
≤
μ
α
(1 − μ)
α
[a; d]
α,Ω
≤ 2
α
μ
α
[a; d]
α,Ω
.
so that a(x
0
) − a
0,B
≤ 2
α
μ
α
[a; d]
α,Ω
.Moreover,
[a(x
0
) − a; d
B
]
α,B
=sup
x,y∈B
d
α
B
(x, y)
|a(x) − a(y)|
|x − y|
α
≤ μ
α
d(x
0
)
α
sup
x,y∈B
d(x, y)
−α
d(x, y)
α
|a(x) − a(y)|
|x − y|
α
≤
μ
α
d(x
0
)
α
(1 − μ)
α
d(x
0
)
α
[a; d]
α,Ω
≤ 2
α
μ
α
[a; d]
α,Ω
.
9.4 Schauder Interior Estimates 341
Combining these two inequalities,
|a(x
0
) − a; d
B
|
α,B
≤ 2
α+1
μ
α
[a; d]
α,Ω
.
Since |a; d|
α,Ω
≤ K by Inequality (9.12),
|(a(x
0
)−a)D
2
u; d
B
|
(2)
α,B
≤ 2
α+1
μ
α
[a; d]
α,Ω
4μ
2
[u; d]
2+0,Ω
+8μ
2+α
[u; d]
2+α,Ω
≤ 32Kμ
2+α
[u; d]
2+0,Ω
+μ
α
[u; d]
2+α,Ω
.
Applying Inequality (7.10) to [u; d]
2+0,Ω
with = μ
α
, there is a constant
C = C(μ, α) such that
|(a(x
0
) − a)D
2
u; d
B
|
(2)
α,B
≤ 64Kμ
2+α
(Cu
0,Ω
+ μ
α
[u; d]
2+α,Ω
). (9.17)
By Inequalities (9.11) and (9.10),
|b
i
D
i
u; d
B
|
(2)
α,B
≤ 8μ
2
|b
i
D
i
u; d|
(2)
α,Ω
≤ 8μ
2
|b
i
; d|
(1)
α,Ω
|D
i
u; d|
(1)
α,Ω
≤ 8Kμ
2
|u; d|
1+α,Ω
.
Applying Inequality (7.10) to |u; d|
1+α,Ω
with = μ
2α
, there is a constant
C = C(μ, α) such that
|b
i
D
i
u; d
B
|
(2)
α,B
≤ 8Kμ
2
Cu
0,Ω
+ μ
2α
|u; d|
2+α,Ω
. (9.18)
Similarly, thereisaconstantC = C(μ, α) such that
|cu; d
B
|
(2)
α,B
≤ 8μ
2
|c; d|
(2)
α,Ω
|u; d|
(0)
α,Ω
≤ 8Kμ
2
(Cu
0,Ω
+ μ
2α
|u; d|
2+α,Ω
). (9.19)
By Inequality (9.11),
|f; d
B
|
(2)
α,B
≤ 8μ
2
|f; d|
(2)
α,Ω
. (9.20)
In combining the above inequalities to estimate |f
0
; d
B
|
(2)
α,B
, it is essential to
keep track of the dependence of constants on the data; in particular, it is
essential that the coefficient of μ
2+2α
[u; d]
2+α,Ω
does not depend upon μ.As
usual, C will be a generic symbol for constants depending upon the data but
the symbol for the coefficient of μ
2+2α
[u; d]
2+α,Ω
will exhibit the dependence
explicitly. Returning to Inequality (9.16) and using Inequalities (9.17), (9.18),
(9.19), and (9.20),
|f
0
; d|
(2)
α,B
≤ Cμ
2
u
0,Ω
+ C(K)μ
2+2α
[u]
2+α,Ω
+ Cμ
2
[f; d]
(2)
α,Ω
.
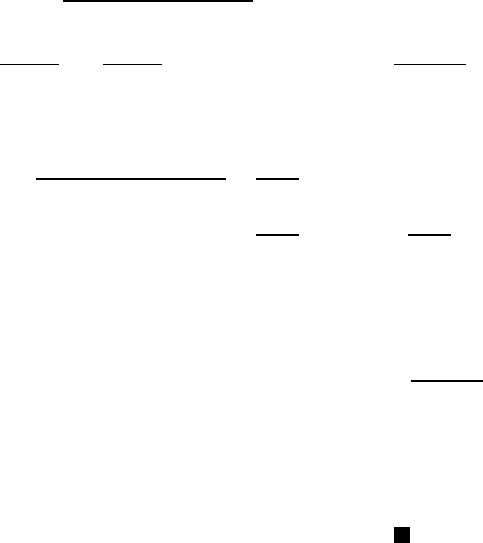
342 9 Elliptic Operators
Returning to Inequality (9.15), for y
0
∈ B
x
0
,δ/2
d(x
0
,y
0
)
2+α
|D
ij
u(x
0
) − D
ij
u(y
0
)|
|x
0
− y
0
|
α
≤ C
u
0,Ω
μ
2+α
+ C
u
0,Ω
μ
α
+ C(K)μ
α
|u; d|
2+α,Ω
+ C
|f; d|
(2)
α,Ω
μ
α
.
(9.21)
Using Inequality (7.10) with = μ
2α
/2
α+1
,fory
0
∈ B
x
0
,δ/2
d(x
0
,y
0
)
2+α
|D
ij
u(x
0
) − D
ij
u(y
0
)|
|x
0
− y
0
|
α
≤
2
α+1
δ
α
d(x
0
)
α
[u; d]
2+0,Ω
≤
2
α+1
μ
α
(Cu
0,Ω
+
μ
2α
2
α+1
[u; d]
2+α,Ω
)
≤ Cu
0,Ω
+ μ
α
[u; d]
2+α,Ω
.
Combining this result with Inequality (9.21),
[u; d]
2+α,Ω
≤ Cu
0,Ω
+ C(K)μ
α
|u; d|
2+α,Ω
+ C
|f; d|
(2)
α,Ω
μ
α
.
Adding |u; d|
2+0,Ω
to both sides and applying Inequality (7.10) with = μ
α
and choosing μ<1/2sothat(C(K)+1)μ
α
< 1/2, there is a constant
C = C(K) such that
|u; d|
2+α,Ω
≤ C
u
0,Ω
+ |f ; d|
(2)
α,Ω
.
Theorem 9.4.4 Let L be an elliptic operator satisfying
|a
ij
; d|
(0)
α,Ω
, |b
i
; d|
(1)
α,Ω
, |c; d|
(2)
α,Ω
≤ K, i, j =1,...,n. (9.22)
If f ∈ H
(2)
α
(Ω; d),α ∈ (0, 1),b∈ (−1, 0],and{u
j
} is a sequence of uniformly
bounded functions in H
(b)
2+α
(Ω; d) satisfying the equation Lu
i
= f on Ω,then
there is a subsequence that converges uniformly on compact subsets of Ω to
afunctionu ∈ H
2+α
(Ω; d) ⊂ H
2+α,loc
(Ω) for which Lu = f on Ω.
Proof: Suppose first that b ∈ (−1, 0). Since d(x) ≤ d(Ω),d(x)
b
≥ d(Ω)
b
,x∈
Ω,andd(Ω)
b
|u
i
; d|
2+α,Ω
≤|u
i
; d|
(b)
2+α,Ω
< +∞,i≥ 1. By Lemma 9.4.3,
|u
i
; d|
2+α,Ω
≤ C
u
i
0,Ω
+ |f ; d|
(2)
α,Ω
≤ C
K
+ |f ; d|
(2)
α,Ω
< +∞ (9.23)
where K
=sup
i≥1
u
i
0,Ω
.Ifb = 0, this inequality follows from the same
lemma. Now let Γ be any compact, convex subset of Ω and choose 0 <
δ<min (1,d(Γ, ∂Ω)sothatΓ ⊂ Ω
δ
.Since|u
i
; d|
2+α,
*
Ω
δ
≤|u; d|
2+α,Ω
≤
C(K
+ |f; d|
(2)
α,Ω
< +∞, it follows from the subsequence selection principle,

9.5 Maximum Principles 343
Theorem 7.2.4, that the sequences {u
i
}, {Du
i
},and{D
2
u
i
} are uniformly
bounded and equicontinuous on Γ .Let{B
j
} be a sequence of balls with
closures in Ω which exhausts Ω. Applying the above argument to each B
−
j
,
there is a function u
(j)
on each B
j
and a subsequence {u
(j)
i
} of the {u
i
}
sequence such that the sequences {u
(j)
i
}, {Du
(j)
i
},and{D
2
u
(j)
i
} converge to
u
(j)
,Du
(j)
,andD
2
u
(j)
, respectively, on B
−
j
. Note that the u
(j)
agree on
overlapping parts of the B
j
. The sequence {u
(i)
i
} is a subsequence of each of
the above sequences and there is a function u on Ω such that the sequences
{u
(i)
i
}, {Du
(i)
i
},and{D
2
u
(i)
i
} converge to u, Du,andD
2
u, respectively, on Ω.
Since Inequality (9.23) holds for each u
(i)
i
,eachtermof|u
(i)
i
|
2+α,Ω
is bounded
by C(K
+ |f ; d|
(2)
α,Ω
); for example,
d(x, y)
2+α
|D
2
u
(i)
i
(x) − D
2
u
(i)
i
(y)|
|x − y|
α
≤ C
K
+ |f ; d|
(2)
α,Ω
,i≥ 1,x,y ∈ Ω.
Letting i →∞and taking the supremum over x, y ∈ Ω and D
jk
, [u; d]
2+α,Ω
<
+∞. Similarly, for the other terms of |u; d|
2+α,Ω
.Thus,u ∈ H
2+α
(Ω; d) ⊂
H
2+α,loc
(Ω).
9.5 Maximum Principles
Although an existence theorem for the Dirichlet problem corresponding to an
elliptic operator L has not been proven, a uniqueness result can be proved us-
ing a weak maximum principle. Before stating the principle, some results
from basic analysis will be reviewed. Consider the quadratic function
Q(y)=
n
p,q=1
c
pq
y
p
y
q
where the n ×n matrix [c
pq
] is a real symmetric matrix. The quadratic form
Q is said to be nonnegative definite if Q(y) ≥ 0 for all y ∈ R
n
;if,in
addition, Q(y) = 0 only when y =0,thenQ is said to be positive definite.
Lemma 9.5.1 If u ∈ C
2
(Ω),x
0
∈ Ω,andu(x
0
)=sup
x∈Ω
(x), then the
matrix [−D
x
i
x
j
(x
0
)] is nonnegative definite.
Proof: Let B = B
x
0
,δ
⊂ Ω and let x ∈ R
n
.Sinceu attains its maximum
value at x
0
,D
x
i
u(x
0
)=0, 1 ≤ i ≤ n. By Taylor’s formula with remainder
(c.f. [1]), for 0 <t|x| <δ,
0 ≥ u(x
0
+ tx) − u(x
0
)=
n
i,j=1
D
x
i
x
j
u(x
0
+ t
x)tx
i
tx
j

344 9 Elliptic Operators
for some 0 <t
<t.Thus,
n
i,j=1
D
x
i
x
j
u(x
0
+ t
x)x
i
x
j
≤ 0.
Letting δ → 0,
n
i.j=1
D
x
i
x
j
u(x
0
)x
i
x
j
≤ 0.
Lemma 9.5.2 Let Ω be a bounded open subset of R
n
and let L be an elliptic
operator with c =0and sup
x∈Ω,1≤i≤n
(|b
i
(x)|/m(x)| < +∞.Ifu ∈ C
0
(Ω
−
)∩
C
2
(Ω) and Lu ≥ 0 on Ω, then u attains its maximum value on ∂Ω; moreover,
if Lu>0 on Ω,thenu cannot attain its maximum value at an interior point
of Ω.
Proof: ItwillbeshownfirstthatifLu>0, then u cannot attain its maxi-
mum value at an interior point of Ω. Suppose u attains its maximum value
at an interior point x
0
of Ω. At such a point, the matrix [−D
ij
u(x
0
)] is real,
symmetric, and nonnegative definite. Since the matrix A =[a
ij
(x
0
)] of coef-
ficients is positive definite, there is a nonsingular matrix S =[s
ij
] such that
A = S
t
S (c.f.,[31]). Since a
ij
(x
0
)=
n
k=1
s
ki
s
kj
,
Lu(x
0
)=−
n
i,j=1
a
ij
(x
0
)(−D
x
i
x
j
u(x
0
))
= −
n
i,j=1
n
k=1
s
ki
s
kj
(−D
x
i
x
j
u(x
0
))
= −
n
k=1
n
i,j=1
s
ki
(−D
x
i
x
j
u(x
0
))s
kj
.
Since the double sum is nonnegative for each k =1,...,n,Lu(x
0
) ≤ 0, a
contradiction. Therefore, u cannot attain its maximum value at an interior
point of Ω if Lu>0onΩ. Suppose now that Lu ≥ 0onΩ. By hypothesis,
there is a constant M
0
such that |b
i
|/m ≤ M
0
,i =1,...,n.Sincea
11
≥ m,
for any constant γ>M
0
Le
γx
1
=(γ
2
a
11
+ γb
1
)e
γx
1
≥ m(x)(γ
2
− γM
0
)e
γx
1
> 0.
For every >0, L(u + e
γx
1
) ≥ Le
γx
1
> 0onΩ. By the first part of the
proof, there is a z = z() ∈ ∂Ω such that u(z)+e
γz
1
≥ u(x)+e
γx
1
for
all x ∈ Ω. Thus, sup
z∈∂Ω
u(z)+ sup
z∈∂Ω
e
γz
1
≥ sup
z∈∂Ω
(u(z)+e
γz
1
) ≥
u(x)+e
γx
1
≥ u(x) for all x ∈ Ω. Letting → 0, sup
z∈∂Ω
u(z) ≥ u(x) for all
x ∈ Ω. Thus, sup
z∈∂Ω
u(z) ≥ sup
x∈Ω
u(x).
Recall that u
+
=max(u, 0) and u
−
=max(−u, 0).

9.5 Maximum Principles 345
Corollary 9.5.3 (Weak Maximum Principle) Let Ω be a bounded open
subset of R
n
and let L be an elliptic operator on Ω with c ≤ 0 and
sup
x∈Ω,1≤i≤n
(|b
i
(x)|/m(x)) < +∞.
If u ∈ C
0
(Ω
−
) ∩ C
2
(Ω) and Lu ≥ 0 or Lu ≤ 0,then
sup
Ω
u ≤ sup
∂Ω
u
+
or inf
∂Ω
u
−
≤ inf
Ω
u,
respectively; if Lu =0,then
sup
Ω
|u|≤sup
∂Ω
|u|.
Proof: Suppose Lu ≥ 0onΩ and let L
1
u = Lu − cu.SinceLu ≥ 0onΩ,
L
1
u ≥−cu on Ω. Letting Ω
+
u
= {x ∈ Ω; u(x) > 0}, L
1
u ≥−cu ≥ 0onΩ
+
u
.
If Ω
+
u
= ∅,thenu ≤ 0onΩ, u
+
=0,andsup
Ω
u ≤ sup
∂Ω
u
+
;ifΩ
+
u
= ∅,
applying the previous lemma to L
1
on Ω
+
u
,u attains its maximum value on
∂Ω
+
u
. But since u =0on∂Ω
+
u
∩Ω, u attains its maximum value on ∂Ω where
u = u
+
. Thus, sup
Ω
u ≤ sup
∂Ω
u
+
. Suppose now that Lu =0onΩ. For any
x ∈ Ω,u(x) ≤ sup
∂Ω
u
+
≤ sup
∂Ω
|u|;sinceL(−u)=0, −u(x) ≤ sup
∂Ω
|u|.
Therefore, |u(x)|≤sup
∂Ω
|u| for all x ∈ Ω.
A uniqueness theorem and comparison principle follow easily from the
weak maximum principle.
Theorem 9.5.4 Let Ω be a bounded open subset of R
n
and let L be an
elliptic operator with c ≤ 0 and sup
x∈Ω,1≤i≤n
(|b
i
(x)|/m(x)) < +∞.Ifu, v ∈
C
0
(Ω
−
) ∩C
2
(Ω) satisfy Lu = Lv on Ω and u = v on ∂Ω,thenu = v on Ω.
If Lu ≥ Lv on Ω and u ≤ v on ∂Ω,thenu ≤ v on Ω.
The weak maximum principle does not exclude the possibility that a func-
tion u satisfying Lu ≥ 0 attains a maximum value at an interior point of Ω as
was the case with the Laplacian for nontrivial functions. A stronger form of
the weak maximum principle is needed to exclude this possibility. The open
set Ω ⊂ R
n
is said to satisfy an interior sphere condition at x
0
∈ ∂Ω if
there is a ball B ⊂ Ω with x
0
∈ ∂B. The upper inner normal derivate of u
at x
0
∈ ∂Ω is defined by
D
+
ν
u(x
0
) = lim sup
t→0
+
u(x
0
+ tν(x
0
)) − u(x
0
)
t
where ν = −n.
Lemma 9.5.5 (Hopf [33], Boundary Point Lemma) Let L be a strictly
elliptic operator on the open set Ω ⊂ R
n
with c ≤ 0 and with |a
ij
|, |b
i
|, |c|≤
K, i, j =1,...,n and let u ∈ C
2
(Ω) satisfy Lu ≥ 0 on Ω.Ifforx
0
∈ ∂Ω,

346 9 Elliptic Operators
(i) u can be extended continuously to x
0
,
(ii) u(x
0
) >u(x) for all x ∈ Ω,and
(iii) the interior sphere condition is satisfied at x
0
,
then the upper inner normal derivative at x
0
satisfies D
+
ν
u(x
0
) < 0 whenever
u(x
0
) ≥ 0; if, in addition, c =0,thenD
+
ν
(x
0
) < 0 regardless of the sign of
u(x
0
).
Proof: Let B = B
y,ρ
0
be a ball in Ω with x
0
∈ ∂B.Fix0<ρ
1
<ρ
0
and
define a function w on the closed annulus A = B
−
y,ρ
0
∼ B
y,ρ
1
by putting
w(x)=e
−γr
2
− e
−γρ
2
0
where ρ
1
<r= |x − y| <ρ
0
and γ is a constant to be specified below. By
Schwarz’s inequality,
Lw(x)=e
−γr
2
4γ
2
n
i,j=1
a
ij
(x
i
− y
i
)(x
j
− y
j
)
− 2γ
n
i=1
(a
ii
+ b
i
(x
i
− y
i
)
+ cw
≥ e
−γr
2
4γ
2
mr
2
− 2γ
n
i=1
a
ii
− 2γ|b|r + c
≥ e
−γr
2
(4γ
2
mρ
2
1
− 2γnK − 2γ
√
nKρ
0
− K).
It follows that γ can be chosen so that Lw ≥ 0onA.Sinceu −u(x
0
) < 0on
∂B
y,ρ
1
,thereisan>0 such that
u − u(x
0
)+w ≤ 0on∂B
y,ρ
1
.
Since w =0on∂B
y,ρ
0
,u− u(x
0
)+w ≤ 0on∂B
y,ρ
0
and therefore on ∂A.
Since L(u − u(x
0
)+w)=Lu − cu(x
0
)+Lw ≥−cu(x
0
) ≥ 0 whenever
u(x
0
) ≥ 0, u − u(x
0
)+w ≤ 0onA by Corollary 9.5.3. For x
0
+ tν ∈ A,
u(x
0
+ tν(x
0
)) − u(x
0
)
t
≤−
w(x
0
+ tν(x
0
))
t
= −
w(x
0
+ tν(x
0
)) − w(x
0
)
t
so that D
+
ν
u(x
0
) ≤−D
+
ν
w(x
0
)=D
r
w|
r=ρ
0
= −2γρ
0
e
−γρ
2
0
< 0. If c =0,
then the preceding steps are valid without any condition on u(x
0
).
Theorem 9.5.6 (Hopf [32], Strong Maximum Principle) Let L be a
strictly elliptic operator on the connected open set Ω ⊂ R
n
with c ≤ 0 and
|a
ij
|, |b
i
|, |c|≤K, i, j =1,...,n,andletu ∈ C
0
(Ω
−
)∩C
2
(Ω) satisfy Lu ≥ 0
on Ω.Thenu cannot attain a nonnegative maximum value at a point of Ω
unless it is constant; if, in addition, c =0and u attains its maximum value
at a point of Ω,thenu is a constant function.

9.6 The Dirichlet Problem for a Ball 347
Proof: Assume that u is nonconstant and attains a nonnegative maximum
value M at an interior point of Ω.LetΩ
M
= {x ∈ Ω; u(x) <M} = ∅.
Under these assumptions, ∂Ω
M
∩ Ω = ∅, for if not, then ∂Ω
M
⊂ ∂Ω which
implies that Ω = Ω
M
∪ (Ω ∼ Ω
M
)=Ω
M
∪ (Ω ∼ Ω
−
M
), contradicting
the fact that Ω is connected. Thus, there is a point x
0
∈ Ω
M
such that
d(x
0
,∂Ω
M
) <d(x
0
,∂Ω). Let B be the largest ball in Ω
M
having x
0
as its
center. Then u(y)=M for some y ∈ ∂B and u<Mon B.SinceΩ
M
satisfies the interior sphere condition at y, the inner normal derivative of u
on B at y is strictly negative according to the preceding lemma. But this is
a contradiction since any directional derivative of u at y must be zero. Thus,
if u attains a nonnegative maximum value at an interior point of Ω,itmust
be a constant function. If, in addition, c = 0, the preceding lemma can be
applied in the same way.
Theorem 9.5.7 (Hopf [32]) Let Ω be a connected open subset of R
n
,letL
be a strictly elliptic operator with c ≤ 0 and locally bounded coefficients. If u ∈
C
0
(Ω
−
) ∩ C
2
(Ω) satisfies Lu ≥ 0 on Ω,thenu cannot attain a nonnegative
maximum value on Ω unless it is constant on Ω. If, in addition, c =0,then
u cannot attain its maximum value on Ω unless it is constant on Ω.
Proof: Suppose M =sup
x∈Ω
−
u(x) ≥ 0andletΩ
M
= {y ∈ Ω; u(y)=
M}.ThenΩ
M
is a relatively closed subset of Ω. Suppose x
0
∈ Ω
M
and
B = B
x
0
,δ
⊂ B
−
x
0
,δ
⊂ Ω. By the preceding theorem, u = M on B since
u(x
0
)=M. Therefore, B ⊂ Ω
M
;thatis,Ω
M
is relatively closed and open in
Ω.SinceΩ is connected, Ω
M
= ∅ or Ω
M
= Ω.
9.6 The Dirichlet Problem for a Ball
It will be assumed in this section that the coefficients of L belong to
H
α,loc
(Ω); in particular, the coefficients belong to H
α
(B) when restricted
toaballB with closure in Ω.
If it were possible to solve the Dirichlet problem corresponding to an ellip-
tic operator L and a ball B, then the Perron-Wiener-Brelot method could be
used to solve the Dirichlet problem for more general regions. The following
lemma reduces to Theorem 9.4.3 when b =0.
Lemma 9.6.1 Let L be a strictly elliptic operator on the bounded open set
Ω ⊂ R
n
satisfying Inequalities (9.12). If u ∈ H
2+α
(Ω; d),α ∈ (0, 1),satisfies
the equation Lu = f on Ω, |u; d|
(b)
0,Ω
< +∞,and|f; d|
(2+b)
α,Ω
< +∞ for b ∈
(−1, 0),then
|u; d|
(b)
2+α,Ω
≤ C
|u; d|
(b)
0,Ω
+ |f ; d|
(2+b)
α,Ω
where C = C(n, α, b).
