Helms L.L. Potential Theory

Подождите немного. Документ загружается.

358 9 Elliptic Operators

on B, Lu = Lw = f on B and u ∈ H

2+α

(B; d). Since w is continuous on B,

u is continuous on B, and since B is an arbitrary ball with closure in Ω, u is

continuous on Ω and Lu = f on Ω. Clearly, u ≥ H

f,g

since each u

∈ U(f,g).

Since u is continuous on Ω and u ≤ inf {v; v ∈ I

},u≤ inf {v; v ∈ U(f,g)} =

f,g

on Ω. Therefore, u = H

f,g

on Ω and LH

f,g

= Lu = f on Ω.

9.8 Barriers

Throughout this section, Ω will be a bounded open subset of R

, L will be

a strictly elliptic operator with c ≤ 0 and coeﬃcients a

,c,i,j =1,...n,

in H

(Ω). Unless noted otherwise, f will be a ﬁxed bounded function in

(2+b)

(Ω; d),α ∈ (0, 1),b∈ (−1, 0).

Under the hypothesis that g is a bounded function on ∂Ω,H

f,g

satisfy the

equations LH

f,g

= f on Ω. In the case of the Laplacian with f =0onΩ,it

was possible to show that every continuous function g on ∂Ω is Δ-resolutive.

This is the statement of Wiener’s theorem, Theorem 2.6.16.

Deﬁnition 9.8.1 If g is a bounded function on ∂Ω that is continuous at

∈ ∂Ω, a sequence of functions {w

} in C

(Ω

−

)isanapproximate

upper barrier at x

for g if

(i) each w

is a supersolution relative to g and

(ii) lim

j→∞

)=g(x

An approximate lower barrier {w

−

} is deﬁned by using subsolution in

place of supersolution. If both an approximate upper barrier and an approxi-

mate lower barrier at x

for g exist, the pair {w

} is called an approximate

barrier at x

for g.

Lemma 9.8.2 Let g be a bounded function on ∂Ω that is continuous at

∈ ∂Ω. If there is an approximate barrier {w

} at x

for g,then

lim

y→x

,y∈Ω

f,g

(y)=g(x

Proof: Since every subsolution for g is less than or equal to every super-

solution for g,

−

≤H

f,g

≤ w

so that

−

(x) − w

−

)+w

−

) − g(x

) ≤H

f,g

(x) − g(x

)

≤ w

(x) − w

)+w

) − g(x

)

9.8 Barriers 359

for x ∈ Ω.Given>0, choose j

≥ 1 such that w

) − g(x

) </2and

−

) − g(x

) > −/2. Then

−

(x) − w

−

) −



≤H

f,g

(x) − g(x

) ≤ w

(x) − w



and since w

∈ C

(Ω

−

−/2 ≤ lim inf

x→x

,x∈Ω

f,g

(x) − g(x

)) ≤ lim sup

x→x

,x∈Ω

f,g

(x) − g(x

)) ≤ /2

and so lim

x→x

,x∈Ω

f,g

(x)=g(x

Lemma 9.8.3 If x

∈ ∂Ω, g is a bounded function on ∂Ω that is continuous

at x

,andw ∈ C

(Ω

−

) ∩ C

(Ω) satisﬁes

(i) Lw ≤−1 on Ω,

(ii) w(x

)=0,and

(iii) w>0 on ∂Ω ∼{x

then for each j ≥ 1 there is a constant γ

> 0 such that the functions w

g(x

)+(1/j)+γ

w and w

−

= g(x

) − (1/j) − γ

w are supersolutions and

subsolutions, respectively, and {w

} is an approximate barrier at x

for g.

Proof: Using the continuity of g at x

,foreachj ≥ 1thereisaneighborhood

U of x

in ∂Ω such that g(x

) −(1/j) ≤ g(x) ≤ g(x

)+(1/j)forx ∈ U .On

∂Ω ∼ U, w is bounded below by a positive constant and it follows that there

is a constant β

> 0 such that

g(x

) −

− β

w(x) ≤ g(x) ≤ g(x

+ β

w(x)forx ∈ ∂Ω.

For each j ≥ 1, let γ

=max(β

, f − c(g(x

)

)andlet

= g(x

) ±

± γ

w on Ω

−

Clearly, w

−

(x) ≤ g(x) ≤ w

(x),x ∈ ∂Ω.SinceLw ≤−1onΩ and c ≤ 0,

= c(g(x

)+(1/j)) + γ

Lw ≤ cg(x

)+(c/j) − γ

≤ f. This shows

that each w

is a superfunction. Since w

)=g(x

)+(1/j) → g(x

)as

j →∞, {w

} is an upper barrier at x

for g. Similarly, {w

−

} is a lower

barrier at x

for g.

By analogy with the classic case, a point x

∈ ∂Ω is called a L-regular

boundary point if lim

y→x

,y∈Ω

f,g

(y)=g(x

) whenever g is bounded on

∂Ω and continuous at x

. The region Ω is called L-regular if each boundary

point is L-regular. It will be shown below that Poincar´e’s exterior sphere

360 9 Elliptic Operators

condition at a point x

∈ ∂Ω suﬃces to show that x

is a L-regular boundary

point; that is, the existence of a ball B with Ω

−

∩B

−

= {x

} suﬃces to prove

L-regularity at x

. Assuming that Ω has a smooth boundary and that the

,c,andf are locally Lipschitz continuous on Ω,Herv´e [30] has shown

that a boundary point x

∈ ∂Ω is L-regular if and only if it is Δ-regular.

The following lemma in conjunction with Lemma 9.8.2 shows that

lim

y→x

,y∈Ω

(y)=g(x

)

if Ω satisﬁes an exterior sphere condition at x

∈ ∂Ω. It will be shown

below that the exterior sphere condition can be replaced by a Zaremba cone

condition.

Lemma 9.8.4 (Poincar´e[50])If the bounded open set Ω satisﬁes an ex-

terior sphere condition at x

∈ ∂Ω, the coeﬃcients of L are bounded, and

g is a bounded function on ∂Ω that is continuous at x

, then there is an

approximate barrier at x

for g.

Proof: Let B = B

y,δ

satisfy the exterior sphere condition at x

,letr = |x−y|,

and let v

(x)=δ

−β

− r

−β

,β > 0.Itcanbeassumedthatδ<1. Since

−β

<δ

−β

for r>δ,

(x)=−β(β +2)r

−β−4



i,j=1

− y

)(x

− y

)

+ βr

−β−2



i=1



+ b

− y

)



+ c(x)



−β

− r

−β



≤ βr

−β−2



(−β − 2)m +



i=1



+ b

− y

)





,x∈ Ω.

Since r

−β−2

<δ

−β−2

for x ∈ Ω and the coeﬃcients of L are bounded, there

is a constant k>0 such that

(x) ≤ βδ

−β−2



(−β − 2)m + k



,x∈ Ω.

Since the right side of this inequality has the limit −∞ as β → +∞,there

is a positive constant β

such that Lv

(x) ≤−1 for all x ∈ Ω. Letting

w(x)=v

(x), Lw(x) ≤−1forx ∈ Ω,w(x

) = 0, and w>0on∂Ω ∼{x

Thus, there is an approximate barrier at x

for g by the preceding lemma.

It was shown in Theorem 2.6.29 that the existence of a cone C in ∼ Ω

with vertex at x

∈ ∂Ω implies that x

is a Δ-regular boundary point for

Ω. By making use of a polar representation of certain functions on Ω, it will

be shown that this same condition can be used to prove the existence of an

approximate barrier at x

for the Dirichlet problem for elliptic operators.

9.8 Barriers 361

The following results from the calculus will be needed to derive the polar

representation. If (ρ, φ) are the polar coordinates of the point (x, y) ∈ R

and

u is a function deﬁned on a neighborhood of (x, y), under suitable conditions

the partial derivatives u

and u

can be converted to polar coordinates as

follows:

∂u

∂x

= u

cos φ −

sin φ (9.29)

∂u

∂y

= u

sin φ +

cos φ (9.30)

The second partials u

,andu

also can be converted to polar coordi-

natesasfollows:

∂

∂x

=cos

∂

∂ρ

− 2

sin φ cos φ

∂

∂ρ∂φ

sin

∂

∂φ

sin φ cos φ

∂u

∂φ

sin

∂u

∂ρ

∂

∂x∂y

=sinφ cos φ

∂

∂ρ



1 − 2sin



∂

∂φ∂ρ

−

sin φ cos φ

∂

∂φ

−

sin φ cos φ

∂u

∂ρ



−1+sin



∂u

∂φ

∂

∂y

=sin

∂

∂ρ

− 2

sin φ cos φ

∂u

∂φ

sin φ cos φ

∂

∂φ∂ρ

cos

∂u

∂ρ

cos

∂

∂φ

In particular, when φ =0

= u

(9.31)

= u

ρρ

ρφ

−

φφ

. (9.32)

For notational convenience, the derivation of a polar representation of a

function at a point x

∈ ∂Ω will be carried out by assuming that x

=0.For

x ∈ R

,letr(x)=|x| and let θ(x)=cos

−1

/r(x)) for x = 0. Functions of

the form u(r, θ) will be considered in order to obtain a polar representation

of Lu on a cone having the x

-axis as its axis of symmetry and of half-angle

; more precisely, if x is a point of the cone, then a polar representation of

Lu(x), dependent upon x, will be derived.

For this purpose, it is convenient to introduce a second coordinate system

dependent upon the ﬁxed point x, which will be referred to as the y-coordinate

system. It is easier to describe the construction of the y-coordinate system in

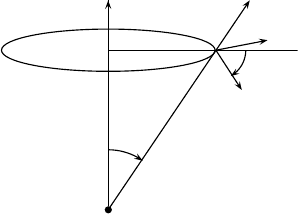
362 9 Elliptic Operators

n−1

Fig. 9.1 Polar Representation

geometrical terms. Consider the sphere r = r(x) and the tangent hyperplane

n−1

(x) to this sphere at x. The unit vector η

= x/|x| is then normal to

n−1

(x)atx.Nowletη

be the unit vector at x tangent to the circle obtained

by intersecting the sphere r = r(x) with the plane spanned by the point x and

the x

-axis, oriented in the direction of increasing θ.Nowletη

,...,η

an orthogonal basis for the orthogonal complement in π

n−1

(x) of the linear

space spanned by η

. Then the vectors η

,...,η

constitute an orthogonal

basis for π

n−1

(x). Then any point y ∈ R

can be written y =



i=1

for

suitable choice of the y

and (y

,...,y

) are the coordinates of y relative to

the y-coordinate system centered at x. After a translation and orthogonal

transformation, a function f in x

,...,x

coordinates induces a function

in y

,...,y

coordinates by the equation

f(y)=f(x + Oy), where O =[o

]

is an orthogonal matrix; in particular,

f(0) = f(x).

If S is any sphere in R

and u is a constant function on S, then the rate of

change of u at any point y of S in the direction of a tangent line at y is zero. In

particular, if (y

, 0,...,0) is any point in the y

-plane and S is a sphere

in R

having center at y = 0 and passing through the point (y

, 0,...,0),

and the function u is constant on S,thenfori ≥ 3, u

=0at(y

, 0,...,0)

since the y

axis is orthogonal to the y

-plane and therefore a tangent line.

Transforming the operator

Lu =



i,j=1

u +



i=1

u + cu

in the x-coordinate system to the y-coordinate system,

Lu =



i,j=1

˜a

u +



i=1

u +˜cu (9.33)

where

A =[˜a

]=O

AO,



i=1

,and˜c(y)=c(x + Oy).

9.8 Barriers 363

Letting S

n−1

denote the sphere obtained by intersecting the cone having

the x

-axisasaxisofsymmetryandhalf-angleθ = θ(x) with the sphere of

radius r = r(x), the function u is constant on S

n−1

and equal to u(r, θ)there.

As remarked above, u

=0,i≥ 3, at any point of the y

-plane. Therefore,

)

(x)=u(y

)

(x)=0,i≥ 3.

Consider the matrix D =[u

] that has the form

D =



0 D

n−2



where D

and D

n−2

are real symmetric matrices of size 2×2and(n−2)×(n−

2), respectively. Thus, there is an orthogonal matrix Q such that QD

n−2

is a diagonal matrix of which the entries on the diagonal are the eigenvalues

of D

n−2

.Ifvariablesz

,...z

are deﬁned by the equation

⎡

⎢

⎣

⎤

⎥

⎦

= Q

⎡

⎢

⎣

⎤

⎥

⎦

then QD

n−2

has the form indicated in the matrix

D =

⎡

⎢

⎣

00... 0

00u

0 ... 0

0000... u

⎤

⎥

⎦

Consider any line  through x that is orthogonal to the y

-plane. The hy-

perplane through  parallel to the y

-axis will intersect S

n−1

in a circle. The

geometrical relationship of the line  to the circle is independent of the line;

that is, by symmetry, any second derivative of u at x in any direction orthog-

onal to the y

-plane is independent of the direction. Hence, u

,i≥ 3, are

all equal. Since these second partials are the eigenvalues of the D

n−2

must be scalar multiple of the identity matrix (c.f. [31], Lemma 9.5.3, and

Exercise 26, p. 386). Since z



j=3

is orthogonal to the y

-plane,

= u

and so u

= u

for j ≥ 3. Therefore,

D =

⎡

⎢

⎣

00... 0

00u

0 ... 0

0000... u

⎤

⎥

⎦

. (9.34)

364 9 Elliptic Operators

Consider now a function u of the form u(r, θ)=r

f(θ)). At any point

)inthey

-plane with polar coordinates (ρ, θ + φ)withpoleat0,the

value of u is u(ρ, θ + φ)=ρ

f(θ + φ). By the ﬁrst equation in (9.32), when

φ =0

= u

ρρ

= λ(λ − 1)ρ

λ−2

f(θ).

At x, ρ = r(x)andso

(x)=λ(λ − 1)r

λ−2

f(θ). (9.35)

Similarly, using the second equation in (9.32),

(x)=u

(x)=r

λ−2

(λ − 1)f



(θ) (9.36)

and using the third equation in (9.32),

= r

λ−2

(λf(θ)+f



(θ)). (9.37)

Expressing u

in terms of r, λ,andf(θ) is more complicated. When y

=0,u is a constant on S

n−1

and has the value u(r, θ)there.Forsuch

points, r =(x

+ R

)

1/2

,whereR = r sin θ so that u is a function of R only

on S

n−1

. Letting (R, ψ) denote polar coordinates in the plane orthogonal to

the x

-axis and passing through the point x, by the third equation of (9.32)

Since u

is the directional derivative of u in any direction radiating from

the conical axis in the x = x

plane, it can be calculated in the y

-plane.

Returning to polar coordinates (ρ, φ)inthey

-plane, u = u(ρ, θ + φ)there.

Note that u

= u

at x and u

= u

when φ =0.Sinceθ is the angle between

the y

-axis and the R-direction as depicted in Figure 9.1,

= u

cos (

− θ)+u

sin (

− θ)

= u

sin θ + u

cos θ.

By translating the y

coordinate system to 0, it is easy to see from

Equations (9.29) and (9.30) that

= u

cos φ −

sin φ

= u

sin φ +

cos φ.

When φ =0,u

= u

and u

=(1/ρ)u

.Atx, u

= u

and u

Therefore,

= u

sin θ +

cos θ

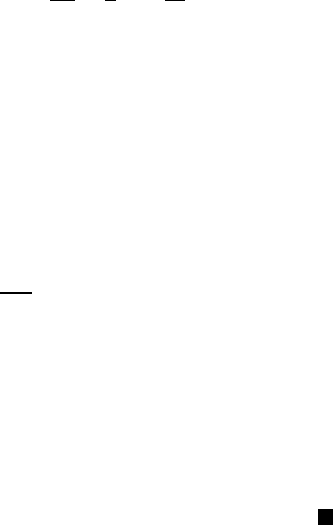
9.8 Barriers 365

and

cot θ = r

λ−2

(λf + f



cot θ). (9.38)

The above calculations of the u

lead to a polar representation of

L(r

f(θ)).

Theorem 9.8.5 (K. Miller [45]) If λ>0 and u = r

f(θ) ∈ C

([0, ∞) ×

[0,π]),then



f(θ)



= r

λ−2



˜a

λ(λ − 1)f +2˜a

(λ − 1)f



+˜a



+ λf )

d(n − 2)(λf + f



cot θ)



+ r

λ−1

(

λf +



+˜crf)

(9.39)

where

d =

n−2



i=3

∈ [m, M] and the eigenvalues of the matrix



˜a



(9.40)

are in [m, M ].

Proof: The above equation follows immediately from Equations (9.35) to

(9.38). Since the eigenvalues of A and its diagonal entries are in the interval

[m, M ], the same is true of

A = O

AO. Since the above matrix is a diagonal

submatrix of

A, its eigenvalues are in [m, M ].

The construction of an approximate barrier at x

∈ ∂Ω depends upon

showing that there is a function w deﬁned on Ω in a neighborhood of x

satisfying the properties listed in Lemma 9.8.3; in particular, the function w

must satisfy the inequality Lw ≤−1onΩ. The function w = r

f(θ) will be

used in the construction of an approximate barrier at x

by choosing f so that

L(r

f(θ))/r

λ−2

< 0onΩ in a neighborhood of x

and then modifying w.

Suppose that every cone C with vertex at x

, no matter how sharp, contains a

point of Ω arbitrarily close to x

. It would then follow that there is a sequence

,θ

)inΩ with limit x

such that the term f



(θ)cotθ

in Equation (9.39)

could become inﬁnite. By postulating that there is a cone C ⊂∼ Ω with

vertex at x

,thetermf



(θ)cotθ canbecontrolledonΩ.

Consider any >0, a positive constant K, and a function f on [0, 2π]

satisfying the diﬀerential equation



− Kf



= −3 (9.41)

subject to the following conditions:

(i) f(0) = 1,f >0on[0, 2π]andf ∈ C

([0, 2π])

(ii) f



(0) = 0 and f



< 0on(0, 2π]

(iii) f



< 0on[0, 2π].

366 9 Elliptic Operators

The function

f(θ)=

3



θ −



+1+

3m

is easily seen to satisfy Equation (9.41) and all of the above conditions save

possibly for the requirement that f(θ) > 0forθ ∈ [0, 2π]. Since the sum on

the right side has the limit 1 uniformly on [0, 2π]as → 0, there is an >0

such that the function f satisﬁes all of the above conditions. The condition

that f (0) = 1 in (i) is only a normalizing constant and any other positive

constant would do as well.

Lemma 9.8.6 If 0 <θ

<π, there are constants 0 <r

< 1, 0 <λ

< 1

andafunctionf ∈ C

([0,π]) such that

L(r

f(θ))

λ−2

≤−1,θ∈ [0,θ

]),r<r

, |λ| <λ

. (9.42)

Proof: Itcanbeassumedthatr<1and|λ| < 1. Fix θ

∈ (0,π)andlet

f be any function as described above. Since f



(θ)cotθ ≤ f



(θ)cotθ

and

˜a



(θ) ≤ mf



(θ)on(0,θ

], it follows from Equation (9.39) that

L(r

f(θ)) ≤ r

λ−2



˜a

λ(λ − 1)f +2˜a

(λ − 1)f



+ mf



+˜a

λf

d(n − 2)(λf + f



cot θ

)



+ r

λ−1

(

f +



+˜crf).

Using the fact that the eigenvalues and diagonal entries of the matrix (9.40)

are in [n, M], it is easily seen that |a

| = |a

|≤M. Moreover, there are

constants A, B > 0 such that

L(r

f(θ)) ≤ r

λ−2



(M|λ||λ − 1| + M |λ| + M (n − 2)|λ|)f + mf



− (2M|λ − 1|+ M (n − 2)|cot θ

|+ A)f





+ Br

λ−1

Now let f be a solution of Equation (9.41) satisfying (i), (ii), and (iii)with

K =4M +M(n−2)|cot θ

|+A. Letting ε

(θ)=M(|λ||λ−1|+|λ|+(n−2)|λ|)

and noting that f ≤ 1,

L(r

f(θ)) ≤ r

λ−2

(mf



− Kf



+ ε

(θ)) + Br

λ−1

where ε

(θ) → 0 uniformly on [0,θ

]asλ → 0. By choice of f,

L(r

f(θ))

λ−2

≤−3 + ε

(θ)+Brf.

Now choose r

> 0and0<λ

< 1 such that ε

(θ) <for θ ∈ (0,θ

], |λ| <λ

and Brf ≤ Br <  for r<r

andthenreplacef/ by f.

9.8 Barriers 367

Corollary 9.8.7 If x

∈ ∂Ω and there is a truncated right circular cone

C ⊂∼ Ω of half-angle 0 <ψ<πwith vertex at x

, then there is 0 <λ

< 1,

a neighborhood U of x

,andafunctionf ∈ C

([0,π]) such that

L(r

f(θ)) < −1, |λ| <λ

, (r, θ) ∈ U ∩ Ω.

Proof: Consider ∼ C ⊃ Ω which is a right circular cone of half-angle θ

π −ψ with vertex at x

. Applying Lemma 9.8.6, there are constants 0 <r

1, 0 <λ

< 1 and a function f ∈ C

(([0,π]) such that

L(r

f(θ))

λ−2

≤−1,θ∈ [0,θ

],r < r

, |λ| <λ

Since r

λ−2

→ +∞ as r → 0, there is a neighborhood U of x

such that

L(r

f(θ)) < −1, |λ| <λ

, (r, θ) ∈ U ∩ Ω.

The condition of the above corollary is known as Zaremba’s cone

condition.

Lemma 9.8.8 If F⊂C

(Ω) ∩ H

(2+b)

(Ω; d) with sup

f∈F

f

0,Ω

≤ M<

+∞, x

∈ ∂Ω, g is bounded on ∂Ω and continuous at x

, and there is a right

circular cone C ⊂∼ Ω of half-angle 0 <ψ<π with vertex at x

,then

lim

y→x

,y∈Ω

f,g

(y)=g(x

) uniformly for f ∈F.

Proof: If {w

} is an approximate barrier at x

for g simultaneously for all

f ∈F,thenw

−

≤H

f,g

≤ w

and the conclusion follows as in Lemma 9.8.2.

It therefore suﬃces to prove that there is an approximate barrier {w

} at x

which applies simultaneously to all f ∈F.Consideranyu in the set

f∈F

(U(f,g) ∩ C

(Ω

−

))

which is nonempty by Lemma 9.7.9. It can be assumed that g(x

)+u is a

supersolution simultaneously for all f ∈Fand u(x

) ≥ 0, for if not, replace u

by |g|

+|u|

+u since g(x

)+|g|

+|u|

+u is a superfunction by Lemma 9.7.4.

Let U

be a neighborhood of x

such that

(i) g(x) <g(x

,x∈ ∂Ω ∩ U

(ii) L(r

(θ)) < −1onU

∩ Ω

where w = r

(θ) is a function of the preceding corollary with λ>0. Now

choose k(j) ≥ 1 such that

(iii) k(j) >M+ |c|



g(x



≥



f − L



g(x





for all f ∈F

(iv)

+ k(j)w>uon ∂U

∩Ω.