Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 39

in Eq. (3.56). The resulting numerical values and signs depend on details

of the functions φ

and the lattice periodic potential V

If we neglect the contributions of the next nearest neighbors in

Eq. (3.56), we can write the total numerator as

N



n,m

ik·(R

−R

)

(δ

n,m



+ δ

n±1,m

) . (3.57)

Inserting Eqs. (3.55) and (3.57) into Eq. (3.51), we obtain

(k)=E





n,m

m,n±1

ik·(R

−R

)

. (3.58)

To analyze this result and to gain some insight into the formation of

energy bands, we now restrict the discussion to the case of an ideal cubic

lattice with lattice vector a,sothat

n±1

= R

± a . (3.59)

Using Eq. (3.59) to evaluate the m summation in (3.58), we see that the

exponentials combine as

ik·a

+ e

−ik·a

=2cos(k · a)

so that the n-summation simply yields a factor N and the ﬁnal result for

the energy is

(k)=E



+2B

cos(k ·a) . (3.60)

Eq. (3.60) describes the tight-binding cosine bands. Schematically two such

bands are shown in Fig. 3.1, one for B

> 0 (lower band) and one for B

< 0

(upper band).

To evaluate the detailed band structure, we need the values of E

and

. Without proof, we just want to mention at this point that for an

attractive potential V

(as in the case of electrons and ions) and p-type

atomic functions φ, B

> 0, whereas for s-type atomic functions, B

< 0.

Between the allowed energy levels, we have energy gaps, i.e., forbidden

energy regions.

In summary, we have the following general results:

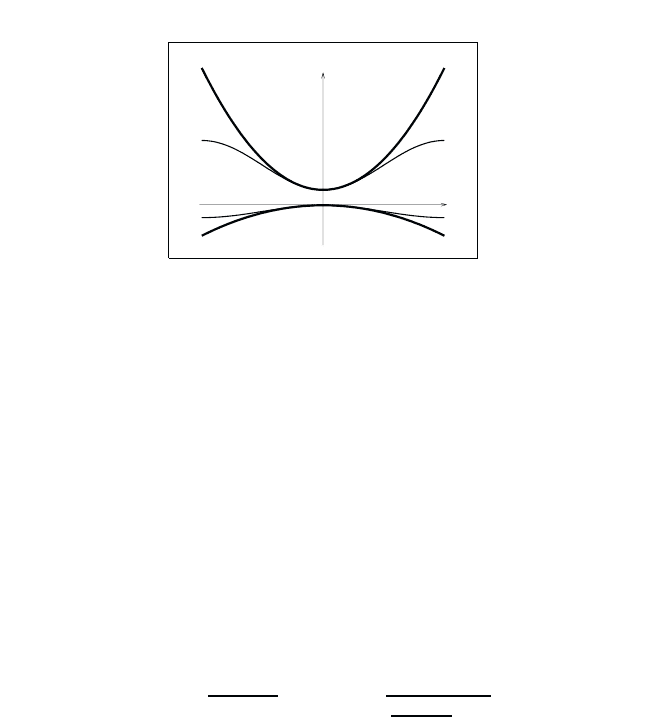
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

40 Quantum Theory of the Optical and Electronic Properties of Semiconductors

Fig. 3.1 Schematic drawing of the energy dispersion resulting from Eq. (3.60) for the

cases of B

> 0 (lower band) and B

< 0 (upper band). The eﬀective mass approxima-

tion results, Eq. (3.61), are shown as the thick lines.

(i) The discrete atomic energy levels become quasi-continuous energy re-

gions, called energy bands, with a certain band width.

(ii) There may be energy gaps between diﬀerent bands.

(iii) Depending on the corresponding atomic functions, the bands E

(k)

may have positive or negative curvature around the band extrema.

(iv) In the vicinity of the band extrema, one can often make a parabolic

approximation

(k)  E

λ,0



λ,ef f



∂

(k)

∂k



k=0

. (3.61)

In the regimes where the parabolic approximation is valid, the electrons

can be considered quasi-free electrons but with an eﬀective mass m

eff

which may be positive or negative, as indicated in Fig. 3.1. A large value

of the overlap integral B

results in a wide band and corresponding small

eﬀective mass m

λ,ef f

(v) Ignoring possible electronic correlation eﬀects and other band structure

subtleties, i.e., at the mean ﬁeld level, one can assume that the states

in the bands are ﬁlled according to the Pauli principle, beginning with

the lowest states. The last completely ﬁlled band is called valence band.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 41

The next higher band is the conduction band.

There are three basic cases realized in nature:

(i) The conduction band is empty and separated by a large band gap from

the valence band. This deﬁnes an insulator. The electrons cannot be

accelerated in an electric ﬁeld since no empty states with slightly dif-

ferent E

are available. Therefore, we have no electrical conductivity.

(ii) An insulator with a relatively small band gap is called a semiconductor.

The deﬁnition of small band gap is somewhat arbitrary, but a good op-

erational deﬁnition is to say that the band gap should be on the order

of or less than an optical photon energy. In semiconductors, electrons

can be moved relatively easily from the valence band into the conduc-

tion band, e.g., by absorption of visible or infrared light.

(iii) If the conduction band is partly ﬁlled, we have a ﬁnite electrical con-

ductivity and hence a metal.

3.3 k·pTheory

In this section, we describe two approximate methods, the k · p perturba-

tion theory and Kane’s k · p theory. This k · p approximation forms the

basis for relatively simple, phenomenological band structure calculations

(Sec. 3-4), which yield a quantitative description for states in the vicinity

of the band gap.

The basic idea behind k · p approximations is to assume that one has

solved the band structure problem at some point k

with high symmetry.

Here, we will take this point as k

=0, which is called the Γ-point of the

Brillouin zone. In particular, we assume that we know all energy eigenvalues

(0) and the corresponding Bloch functions u

=0, r)=u

(0, r).In

order to compute the Bloch functions u

(k, r) and the corresponding energy

eigenvalues E

(k) for k in the vicinity of the Γ-point, we expand the lattice

periodic function u

(k, r) in terms of the function u



(0, r),whichforma

complete set.

We write Eq. (3.31) in the form of





k · p



(k, r)=E

(k)u

(k, r) , (3.62)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

42 Quantum Theory of the Optical and Electronic Properties of Semiconductors

where

+ V

(r) (3.63)

and

(k)=E

(k) −



. (3.64)

In second-order nondegenerate perturbation theory, we get

(k)=E

(0) +



η=λ



(k ·λ|p|η)(k ·η|p|λ)

(0) − E

(0)

(3.65)

and

|k,λ = |λ +





η=λ

|ηk ·η|p|λ

(0) − E

(0)

. (3.66)

There is no ﬁrst-order energy correction in Eq. (3.65), since by parity

λ|p|λ =0 . (3.67)

We use here the Dirac notation with the state vectors |k,λ and |k =0,λ≡

|λ. The corresponding Bloch functions are the real space representations of

these vectors, i.e., u

(k, r)=r|k,λ. We consider as the simplest example

two states called |0 and |1 with the energies E

= E

and E

=0.With

0|p

|1 = p

we ﬁnd

0,1

(k)=E

0,1





i,j



∗

, (3.68)

where the +(−) sign is for E

). The energy has a quadratic k-

dependence, so that it is meaningful to introduce the eﬀective mass tensor



eff





∗



. (3.69)

In isotropic cases, such as in cubic symmetry, the eﬀective masses are scalar

quantities

1 ±

with i = c, v . (3.70)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 43

For a suﬃciently large momentum matrix element, the eﬀective mass of the

lower (valence) band can become negative, as is the case for the example

shown in Fig. 3.1, while the eﬀective mass of the conduction band becomes

much smaller than the free electron mass.

Eq. (3.70) shows that the eﬀective masses are determined by the inter-

band matrix element of the momentum operator and by the energy gap. Be-

cause the eﬀective masses can be measured experimentally, one frequently

uses this relation to express the interband momentum matrix element in

terms of the eﬀective electron mass m

= m

and the hole mass m

= −m

Eq. (3.70) allows one to express p

in terms of the reduced electron–hole

mass m

. (3.71)

This result is often used to estimate the value of p

Next, we have to consider the case that some of the bands are degener-

ate. In the element semiconductors of group IV, the four electrons in the

outer shell of the atoms populate the sp

orbitals. The same is true for the

isoelectronic compound semiconductors of the groups III–V and II–VI. In

a cubic symmetry, the valence band states at k =0are made up of three

degenerate p-like states. The conduction band at k =0consists of an s-like

state. Thus, at the center of the Brillouin zone we can approximate the

cubic symmetry, which is the only case we consider here, by a spherical

one and use in the following the eigenfunctions of the angular momentum

operator as basis states. These four states are |l =0,m

=0 = |0, 0, |l =

1,m

= ±1 = |1, ±1 and |l =1,m

=0 = |1, 0. Following Kane, we

diagonalize the Hamiltonian H = H

+ k · p/m

in the basis of these four

states. A linear combination of these states at a ﬁnite wave vector k is

|ψ(k) =





=0,1,|m



|≤l



(k)|l





 . (3.72)

From the stationary Schrödinger equation (3.62) we get

l, m



(k · p) − E(k)|ψ(k) =0 . (3.73)

With the selection rules (see problem 3.4)

l, m

|k · p|l





 = kpδ

l,l



±1



(3.74)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

44 Quantum Theory of the Optical and Electronic Properties of Semiconductors

we ﬁnd the secular equation







− E 0 Ak 0

0 E

− E 00

Ak 0 E

− E 0

000E

− E







=0 (3.75)

with A = p/m

. Rows one through four of (3.75) correspond to the angular

momentum quantum numbers (l, m

) in the order (0,0), (1,1), (1,0), and

(1,-1), respectively.

Evaluation of the determinant (3.75) yields the fourth-order equation

− E)(E

− E)



− E)(E

− E) − A



=0 , (3.76)

which has the two unchanged solutions

E = E



, (3.77)

and the two modiﬁed solutions

E =





1 ±





, (3.78)

where E

= E

and E

=0has been used. Expanding the nonparabolic

dispersion (3.78) up to second order, we ﬁnd again the eﬀective masses of

Eq. (3.70).

Eq. (3.77) shows that two degenerate valence bands still have a positive

curvature with eﬀective masses equal to the free-electron mass. Hence, this

result cannot describe the situation found in direct-gap semiconductors

where all valence bands have a negative eﬀective mass around the Γ-point.

This failure is due to the omission of all states other than the sp

states.

Furthermore, in crystals with cubic symmetry only two bands are de-

generate at k =0, while the third band is shifted to lower energies. It turns

out that the spin–orbit interaction, which has not been considered so far, is

responsible for this split-oﬀ. To ﬁx these shortcomings, we introduce in the

next section a method which takes into account the spin and the spin–orbit

interaction and, at least phenomenologically, the inﬂuence of other bands.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 45

3.4 Degenerate Valence Bands

For a more realistic treatment of the semiconductor valence bands around

the Γ-point, we now take also the spin into account. In the presence of

spin–orbit interaction, only the total angular momentum, i.e. the sum of

the orbital and spin angular momentum, is a conserved quantity. From

the three valence band states |l =1,m

= ±1 =1/

√

2|X ± iY  and

|l =1,m

=0 = |Z and the spin states |↑and |↓one can form the

eigenstates of the total angular momentum operator

J = L + s . (3.79)

Since |l − s|≤j ≤ l + s, the six eigenstates of J,whichresultfromthe

states with l =1and s =1/2, have the quantum numbers j =3/2,m

±3/2, ±1/2 and j =1/2, m

= ±1/2.Thestatewithj =3/2 and m

±3/2 can be expressed in terms of the product states

|3/2, ±3/2 = |m

= ±1,



↑

↓



 , (3.80)

where the upper (lower) sign and the upper (lower) spin orientation belong

together. From these states, one gets by applying the ﬂip-ﬂop operators

(see problem 3.5) the states with m

= ±1/2:

|3/2, ±1/2 =

√



√

2|m

=0,



↑

↓



 + |m

= ±1,



↓

↑







. (3.81)

The states with j =1/2 and m

= ±1/2 are the antisymmetric combina-

tions of the two states in Eq. (3.81), so that an orthogonal state results

|1/2, ±1/2 =

√



−|m

=0,



↑

↓



 +

√

2|m

= ±1,



↓

↑







. (3.82)

The spin–orbit interaction, which can be obtained from relativistic quantum

mechanics, splits the two j =1/2 states oﬀ to lower energies. For simplicity,

we neglect these two split-oﬀ states in the following.

The remaining task is to diagonalize the Hamiltonian by forming a linear

combination of the four j =3/2 states. If we simply apply Kane’s diago-

nalization concept to these four states coupled to an s state, we would still

get a valence band with positive curvature, because the inﬂuence of the

other bands has not yet been incorporated. To overcome this diﬃculty,

one often uses a phenomenological Hamiltonian for the four j =3/2 states

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

46 Quantum Theory of the Optical and Electronic Properties of Semiconductors

which are degenerate at the Γ-point with E(0) = 0. The general form of a

Hamiltonian which is quadratic in k, invariant under rotations, and which

can be constructed with the two vectors k and J is

H =







− 2γ

(k · J)



. (3.83)

Hamiltonian for heavy- and light-hole bands in

spherical approximation

Here, the energy is counted as hole energy (E

= −E

) with the origin at

the top of the valence bands. For later comparison, the constants which

appear in front of the invariant scalars k

and k ·J

in (3.83) have been

expressed in terms of the phenomenological Luttinger parameters γ

α = γ

5γ

and β =2γ

. (3.84)

Because of the spherical symmetry, the result has to be independent of the

direction of the k-vector.

If we take the wave vector as k= ke

, the Hamiltonian (3.83) is already

diagonal for the four J =3/2 states and has the two twofold degenerate

energy eigenvalues

E =



− 2γ



, (3.85)

where m

is the eigenvalue of J

. The two resulting energy eigenvalues are

=(γ

− 2γ

)



for m

= ±

and

=(γ

+2γ

)



for m

= ±

. (3.86)

and E

are the energies of the heavy-hole and light-hole valence bands,

respectively. These two bands are still degenerate at the Γ-point, but the

degeneracy is lifted at ﬁnite k-values due to the diﬀerent eﬀective hole

masses

(γ

− 2γ

) (3.87)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 47

and

(γ

+2γ

) . (3.88)

The two Luttinger parameters, γ

and γ

, can be adjusted so that

Eqs. (3.87) and (3.88) yield the heavy and light-hole mass which are mea-

sured experimentally.

Luttinger considered a more general Hamiltonian acting on the four

j =3/2 states, which is invariant only under the symmetry operations of

the cubic symmetry group:

H =



−





i,j

[γ

− (γ

− γ

)δ

] K

(3.89)

Luttinger’s hole band Hamiltonian for cubic symmetry

where

=3k

− δ

(3.90)

and

+ J

) − δ

. (3.91)

Thetracesofthetwotensors

K and J vanish. If the two Luttinger param-

eters γ

and γ

are equal, the Luttinger Hamiltonian reduces again to the

form (3.83) with the only diﬀerence that k cannot be oriented arbitrarily in

cubic symmetry. The x and y components of the total angular momentum

operators are J

=(J

+ J

−

)/2 and J

=(J

− J

−

)/2i. J

and J

−

are

the ﬂip-ﬂop operators which raise or lower the quantum number m

of J

by one, see also problem 3.5. Note, that the eigenvalue of the operator

J

 = j(j +1). Therefore, in general, the operators J

connect the four

j =3/2 states, and the Luttinger Hamiltonian has to be diagonalized by a

linear combination of the four states. After some algebraic work one gets

the energy eigenvalues

E(k)=E(0) +





+ C

+ k

)



. (3.92)

The constants are given in terms of the Luttinger parameters γ

A = γ

,B=2γ

= 12(γ

− γ

) . (3.93)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

48 Quantum Theory of the Optical and Electronic Properties of Semiconductors

The Luttinger parameters for many semiconductor materials can, e.g., be

found in Landolt–Börnstein. Typical values for some III–V semiconductors

are

GaAs 6.85 2.1 2.9

InAs 19.67 8.37 9.29

InP 6.35 2.08 2.76 .

(3.94)

It is almost always true that

>γ

 γ

. (3.95)

So one sees again that the assumption of spherical symmetry is a good

approximation.

REFERENCES

Extended introductions to and treatments of band structure theory can be

found in the following literature:

N.W. Ashcroft and N.D. Mermin, Solid State Physics, Saunders College

(HRW), Philadelphia (1976)

J. Callaway, Quantum Theory of the Solid State,PartA, Academic Press,

New York (1974)

M.L. Cohen and J.R. Chelikowsky, Electronic Structure and Optical Prop-

erties of Semiconductors, Springer Solid State Sciences Vol. 75, Springer,

Berlin (1988)

E.O. Kane, p.75inSemiconductors and Semimetals,editedbyR.K.

Willardson and A.C. Beer, Academic, New York (1966)

C. Kittel, Introduction to Solid State Physics, Wiley and Sons, New York

(1971)

J.M. Luttinger and M. Kohn, Phys. Rev. 97, 869 (1955)