Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Chapter 3

Periodic Latice of Atoms

After our discussion of the basic optical properties of a single atom in

Chap. 2, we now analyze how the atomic energy spectrum is modiﬁed in

a solid. As our model solid, we take a perfect crystal, where the ions are

arranged in a periodic lattice. In the spirit of a Hartree–Fock or mean ﬁeld

theory, we assume that the inﬂuence of this periodic arrangement of ions on

a given crystal electron can be expressed in the form of an eﬀective periodic

lattice potential which contains the mean ﬁeld of the nuclei and all the other

electrons.

For simplicity, we consider only ideal crystals, which consist of a perfect

ionic lattice and some electrons which experience the lattice periodic poten-

tial. We are interested in the wave functions and allowed energy states of a

single electron moving in the eﬀective lattice potential V

(r). Many-electron

eﬀects will be discussed in later chapters of this book.

3.1 Reciprocal Lattice, Bloch Theorem

For the valence electrons in a crystal, the lattice potential V

(r) is an at-

tractive potential due to the superposition of the Coulomb potentials of the

nuclei and the inner electrons of the ions. However, for our considerations

we never need the explicit form of V

(r). We only utilize some general

features, such as the symmetry and periodicity properties of the potential

which reﬂect the structure of the crystal lattice.

The periodicity of the eﬀective lattice potential is expressed by the trans-

lational symmetry

(r)=V

(r + R

) , (3.1)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

30 Quantum Theory of the Optical and Electronic Properties of Semiconductors

where R

is a lattice vector, i.e., a vector which connects two identical

sites in an inﬁnite lattice, which are n lattice cells apart. It is convenient

to expand the lattice vectors



, (3.2)

where n

are integers and a

are the basis vectors which span the unit cells.

Note, that the basis vectors are not unit vectors and they are generally not

even orthogonal. They point into the directions of the three axes of the

unit cell, which may have e.g. a rhombic or more complicated shape. The

basis vectors are parallel to the usual Cartesian unit vectors only in the

case of orthogonal lattices such as the cubic one.

To make use of the fact that the potential acting on the electron has

the periodicity of the lattice, we introduce a translation operator T

f(r)=f (r + R

) , (3.3)

where f is an arbitrary function. Applying T

to the wave function ψ of

an electron in the periodic potential V

(r),weobtain

ψ(r)=ψ(r + R

)=t

ψ(r) , (3.4)

where t

is a phase factor, because the electron probability distributions

|ψ(r)|

and |ψ(r + R

have to be identical. Since the Hamiltonian

H =

+ V

(r) (3.5)

has the full lattice symmetry, the commutator of H and T

vanishes:

[H,T

]=0 . (3.6)

Under this condition a complete set of functions exists which are simulta-

neously eigenfunctions to H and T

Hψ

(k, r)=E

(k, r) (3.7)

and

(k, r)=ψ

(k, r + R

)=t

(k, r) . (3.8)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 31

Here, we introduced k as the quantum number associated with the trans-

lation operator. As discussed above, t

can only be a phase factor with the

properties

| =1 , (3.9)

and

= t

n+m

(3.10)

since

n+m

= T

, (3.11)

stating the obvious fact that a translation by R

+ R

is identical to a

translation by R

followed by another translation by R

. A possible choice

to satisfy Eqs. (3.8) – (3.11) is

= e

i(k·R

+2πN)

, (3.12)

where 2πN is an allowed addition because

i2πN

=1,forN = integer . (3.13)

We now deﬁne a reciprocal lattice vector g through the relation

ik·R

≡ e

i(k+g)·R

(3.14)

so that g · R

=2πN. Expanding g in the basis vectors b

of the reciprocal

lattice

g =



i=1

= integer , (3.15)

we ﬁnd

g ·R



·a

=2πN , (3.16)

· a

=2πδ

,i,j=1, 2, 3 . (3.17)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

32 Quantum Theory of the Optical and Electronic Properties of Semiconductors

Consequently, b

is perpendicular to both a

and a

with i = k,j and can

be written as the vector product

= c a

× a

. (3.18)

To determine the proportionality constant c,weuse

·b

= c a

·(a

× a

)=2π, (3.19)

which yields

c =

2π

· (a

× a

)

. (3.20)

Hence,

=2π

× a

·(a

× a

)

. (3.21)

Similarly, we can express the a

in terms of the b

In summary, we have introduced two lattices characterized by the unit

vectors a

and b

, respectively, which are reciprocal to one another. Since

the a

are the vectors of the real crystal lattice, the lattice deﬁned by the

is called the reciprocal lattice. The unit cells spanned by the a

are

called the Wigner–Seitz cells, while the unit cells spanned by the b

are the

Brillouin zones. One can think of a transformation between the real and

reciprocal lattice spaces as a discrete three-dimensional Fourier transform.

For the example of a cubic lattice, we have

| =

2π

. (3.22)

Consequently, the smallest reciprocal lattice vector in this case has the

magnitude

2π

. (3.23)

Going back to Eq. (3.14), it is clear that we can restrict the range of k

values to the region

−

≤ k

≤

, (3.24)

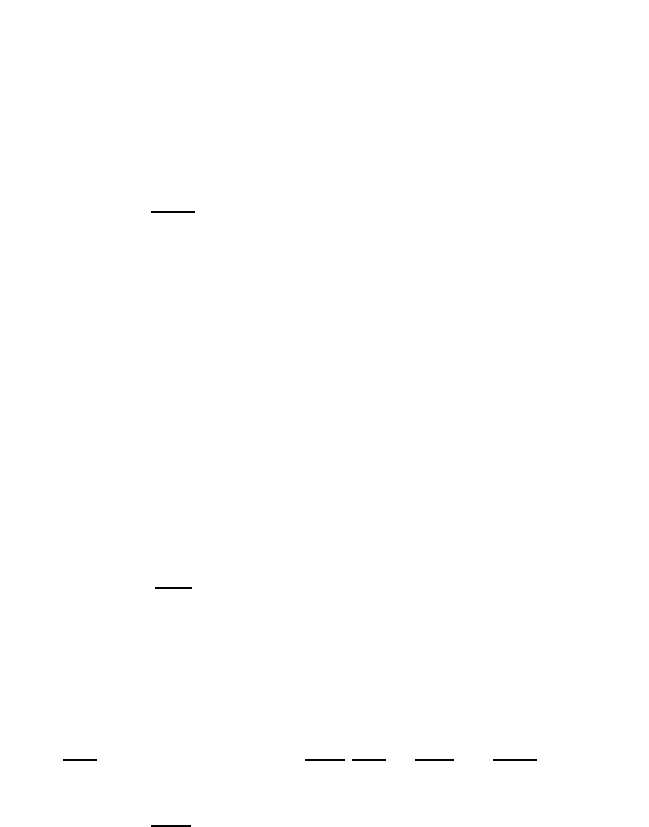
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 33

since all other values of k can be realized by adding (or subtracting) multiple

reciprocal lattice vectors. This range of k-values is called the ﬁrst Brillouin

zone.

Considerations along the lines of Eqs. (3.1) – (3.14) led F. Bloch to

formulate the following theorem, which has to be fulﬁlled by the electronic

wave functions in the lattice:

ik·R

(k, r) = ψ

(k, r+R

) . (3.25)

Bloch theorem

To satisfy this relation, we make the ansatz

(k, r) =

ik·r

3/2

(k, r) , (3.26)

Bloch wave function

where L

is the volume of the crystal and λ is the energy eigenvalue. k

is the eigenvalue for the periodicity (crystal momentum). The function

(k, r) is often called Bloch function. The ansatz (3.26) fulﬁlls the Bloch

theorem (3.25), if the Bloch function u

is periodic in real space

(k, r)=u

(k, r + R

) , (3.27)

i.e. the Bloch function u

(k, r) has the lattice periodicity.

The Schrödinger equation for a crystal electron is

Hψ

(k, r)=



+ V

(r)



(k, r)=E

(k)ψ

(k, r) , (3.28)

where m

is the free electron mass. Inserting Eq. (3.26) into (3.28) and

using the relation



∂

∂x

= −k

+2i



ik·r

3/2

∂u

∂x

ik·r

3/2



∂

∂x

ik·r

3/2

(∇ + ik)

, (3.29)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

34 Quantum Theory of the Optical and Electronic Properties of Semiconductors

we obtain



−



(∇ + ik)

+ V

(r)



(k, r)=E

(k)u

(k, r) . (3.30)

With p = −i∇ Eq. (3.30) can be written in the form



−



∇



k·p + V

(r)



(k, r)=



(k) −





(k, r), (3.31)

which will be the starting point for the k · p analysis in Sec. 3.3.

Before we describe some approximate solutions of Eq. (3.31), we ﬁrst dis-

cuss in the remainder of this section further general properties of the Bloch

wave function. The wave functions (3.26) are complete and orthonormal,



rψ

∗

(k, r)ψ





, r)=δ

λ,λ



k,k



, (3.32)

since they are eigenfunctions of the crystal Hamiltonian, Eq. (3.5). In

Eq. (3.32), we normalized the Bloch functions to the crystal volume L

,so

that



r|ψ

(k, r)|

=1=



r|u

(k, r)|

. (3.33)

The convenient normalization of the wave functions to the volume L

needs some comments, since all real crystals with ﬁnite volume have sur-

faces and thus they do not have the full translational symmetry which we as-

sumed above. However, the problems related to the surfaces can be avoided

through a trick, i.e., the introduction of periodic boundary conditions.Let

us assume the crystal has an end face in z direction at z = L = N

|.Pe-

riodic boundary conditions imply that one assumes the crystal end face to

be connected with the front face at z =0. Generalizing this concept to all

space dimensions, the electron wave functions have to satisfy the condition

(k, r + N

)=ψ

(k, r) , (3.34)

where N

is the total number of unit vectors in the direction i.These

periodic boundary conditions are convenient since they eliminate the surface

but keep the crystal volume ﬁnite.

Using the periodic boundary conditions in the plane wave factor of

Eq. (3.26) implies

ik·(R

)

= e

ik·R

, (3.35)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 35

which is satisﬁed if N

k · a

=2πM,whereM is an integer. In a cubic

lattice,

−

≤ k ≤

(3.36)

and M is therefore restricted:

|M| = |k · a

2π

≤

or −

≤ M ≤

. (3.37)

The Bloch form of the electron wave function in a crystal, Eq. (3.26),

consists of an envelope function and a Bloch function u

.Theenvelope

function for an inﬁnite crystal, or a crystal with periodic boundary condi-

tions, has the form of a plane wave, exp(ik·r). While the Bloch function

varies spatially on an atomic scale, the envelope function varies for small

k-values only on a much longer, mesoscopic scale. Here we say mesoscopic

scale rather than macroscopic scale, because in a real crystal the quantum

mechanical coherence is usually not maintained over macroscopic distances.

Coming back to the normalization integral in Eq. (3.33), we notice that

since the Bloch functions u

have the periodicity of the lattice, the integral

over the crystal volume can be evaluated as



→





, (3.38)

where l

is the volume of an elementary cell, so that L

= Nl

when N is

the number of elementary cells. Substituting Eq. (3.27) into Eq. (3.33) we

obtain



n=1



(k, r)|



r|u

(k, r)|

=1 , (3.39)

showing that the Bloch functions are normalized within an elementary cell.

Furthermore one can show that the Bloch functions are a complete set for

any ﬁxed momentum value



∗

(k, r)u

(k, r



)=l

δ(r − r



) . (3.40)

Sometimes it is useful to introduce localized functions as expansion set

instead of the delocalized Bloch functions u

. An example of such localized

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

36 Quantum Theory of the Optical and Electronic Properties of Semiconductors

functions are the Wannier functions w

(r − R

). The Wannier functions

are related to the Bloch functions via

(r − R

√



ik·(r−R

)

(k, r) (3.41)

and

(k, r)=





−ik·(r−R

)

(r − R

) . (3.42)

It may be shown that the Wannier functions are concentrated around a

lattice point R. They are orthogonal for diﬀerent lattice points



∗

(r)w



(r − R

)=δ

λ,λ



n,0

, (3.43)

see problem 3.2. Particularly in spatially inhomogeneous situations it is

often advantageous to use Wannier functions as the expansion set. The full

electron wave function expressed in terms of Wannier functions is

(k, r)=

√



ik·R

(r − R

) . (3.44)

3.2 Tight-Binding Approximation

After these symmetry considerations, we discuss simple approximations for

calculating the allowed energies and eigenfunctions of an electron in the

crystal lattice. First we treat the so-called tight-binding approximation

which may serve as elementary introduction into the wide ﬁeld of band

structure calculations. In Sec. 3-3 and 3-4, we then introduce more quan-

titative approximations which are useful to compute the band structure in

a limited region of k-space.

In the tight-binding approximation, we start from the electron wave

functions of the isolated atoms which form the crystal. We assume that the

electrons stay close to the atomic sites and that the electronic wave func-

tions centered around neighboring sites have little overlap. Consequently,

there is almost no overlap between wave functions for electrons that are

separated by two or more atoms (next-nearest neighbors, next-next near-

est neighbors, etc). The relevant overlap integrals decrease rapidly with

increasing distance between the atoms at sites m and l, so that only a few

terms have to be taken into account.

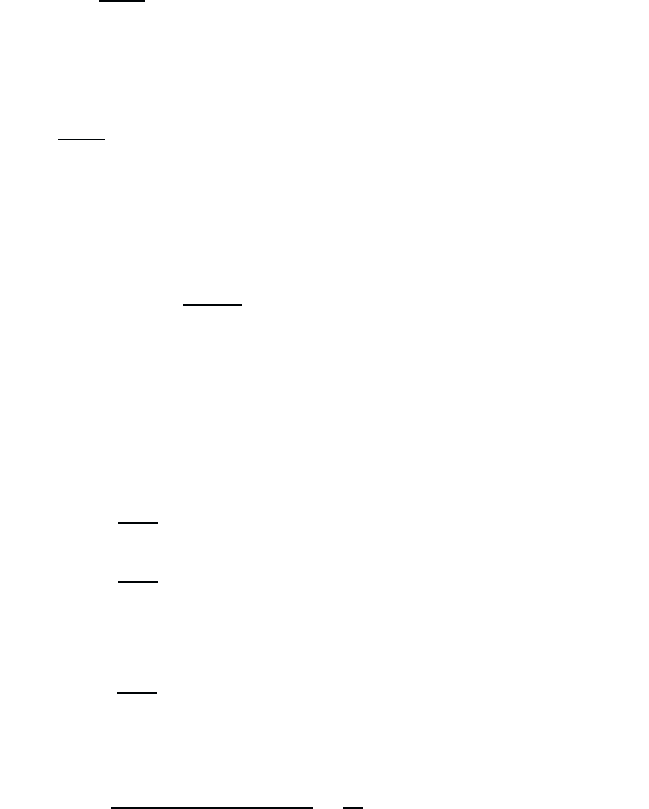
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Periodic Lattice of Atoms 37

The Schrödinger equation for a single atom located at the lattice point

l is

(r − R

)=E

(r − R

) (3.45)

with the Hamiltonian

= −



∇

+ V

(r − R

) , (3.46)

where V

(r − R

) is the potential of the l-th atom. The full problem of the

periodic solid is then



−



∇



(r − R

) − E

(k)



(k, r)=0 . (3.47)

The total potential is the sum of the single-atom potentials. To solve

Eq. (3.47), we make the ansatz

(k, r) =



ik·R

3/2

(r − R

) , (3.48)

tight-binding wave function

which obviously fulﬁlls the Bloch theorem, Eq. (3.25). With the periodic

boundary conditions (3.34) we obtain

ψ(k, r)=

3/2



ik·R

(r − R

)

3/2



ik·R

(r + N

− R

) . (3.49)

Denoting R

− N

= R

, we can write the last line as

ψ(k, r)=

3/2



ik·(R

)

(r − R

) . (3.50)

In order to compute the energy, we have to evaluate

(k)=



rψ

∗

(k, r)Hψ

(k, r)



rψ

∗

(k, r)ψ

(k, r)

, (3.51)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

38 Quantum Theory of the Optical and Electronic Properties of Semiconductors

where the numerator can be written as

N =



n,m

ik·(R

−R

)



rφ

∗

(r − R

)Hφ

(r − R

) (3.52)

and the denominator is

D =



n,m

ik·(R

−R

)



rφ

∗

(r − R

)φ

(r − R

) . (3.53)

Since we assume strongly localized electrons, the integrals decrease rapidly

with increasing distance between site n and m. The leading contribution is

n = m,thenn = m ± 1, etc. In our ﬁnal result, we only want to keep the

leading order of the complete expression (3.51). Therefore, it is suﬃcient

to approximate in the denominator:



rφ

∗

(r − R

)φ

(r − R

)  δ

n,m

, (3.54)

so that

D =



n,m



. (3.55)

We denote the integral in the numerator as

I =



rφ

∗

(r − R

)



−



∇



(r − R

)



(r − R

) .

It can be approximated as follows

I = δ

n,m







l,n



l=n



rφ

∗

(r − R

)φ

(r − R

)





+ δ

n±1,m





rφ

∗

(r + R

n±1

(r − R

)φ

(r + R

)+...

≡ δ

n,m



+ δ

n±1,m

+ ... , (3.56)

where E



is the renormalized (shifted) atomic energy level and B

is the

overlap integral. Energy shift and overlap integral for the states λ usually

have to be determined numerically by evaluating the integral expressions