Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Atoms in a Classical Light Field 19

Inserting (2.10) and (2.11) into Eq. (2.6), we obtain in order ∆

(0)

=0 , (2.12)

which is satisﬁed by

(0)

= δ

n,l

. (2.13)

In ﬁrst order of ∆,wehave

i

(1)

= −E(t)d

−i

. (2.14)

For n = l there is no ﬁeld-dependent contribution, i.e., a

(i)

≡ 0 for i ≥ 1,

since d

=0. Integrating Eq. (2.14) for n = l from −∞ to t yields

(1)

(t)=−

i



−∞



E(t



−i



, (2.15)

where a

(1)

(t = −∞)=0has been used. This condition is valid since we

assumed that the electron is in state l without the ﬁeld, Eq. (2.9).

To solve the integral in Eq. (2.15), we express the ﬁeld through its

Fourier transform

E(t) = lim

γ→0



dω

2π

E(ω)e

−iωt

γt

. (2.16)

Here, we introduced the adiabatic switch-on factor exp(γt), to assure that

E(t) → 0 when t →−∞. We will see below that the switch-on parameter γ

plays the same role as the inﬁnitesimal damping parameter of Chap. 1. The

existence of γ makes sure that the resulting optical susceptibility has poles

only in the lower half of the complex plane, i.e., causality is obeyed. For

notational simplicity, we will drop the lim

γ→0

in front of the expressions,

but it is understood that this limit is always implied. Inserting Eq. (2.16)

into Eq. (2.15) we obtain

(1)

(t)=−





dω

2π

E(ω)

−i(ω+

ω + 

+ iγ

, (2.17)

whereweletγ → 0 in the exponent after the integration.

If we want to generate results in higher-order perturbation theory, we

have to continue the iteration by inserting the ﬁrst-order result into the

RHS of (2.6) and calculate this way a

(2)

etc. These higher-order terms

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

20 Quantum Theory of the Optical and Electronic Properties of Semiconductors

contain quadratic and higher powers of the electric ﬁeld. However, we are

limiting ourselves to the terms linear in the ﬁeld, i.e. we employ linear

response theory.

The total wave function (2.5) is now

ψ(r,t)=e

−i



(r)

−



m=l



(r)



dω

2π

E(ω)

−iωt

ω + 

+ iγ



+ O(E

) . (2.18)

The ﬁeld-induced polarization is given as the expectation value of the

dipole operator

P(t)=n



rψ

∗

(r,t)dψ(r,t) , (2.19)

where n

is the density of the mutually independent (not interacting) atoms

in the system. Inserting the wave function (2.18) into Eq. (2.19), and keep-

ing only terms which are ﬁrst order in the ﬁeld, we obtain the polarization

P(t)=−n







dω

2π



E(ω)

−iωt

ω + 

+ iγ

+ E

∗

(ω)

iωt

ω + 

− iγ



(2.20)

In the integral over the last term, we substitute ω →−ω and use E

∗

(−ω)=

E(ω), which is valid since E(t) is real. This way we get

P(t)=−n







dω

2π

E(ω)e

−iωt



ω + 

+ iγ

−

ω − 

+ iγ





dω

2π

P(ω)e

−iωt

. (2.21)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Atoms in a Classical Light Field 21

This equation yields P(ω)=χ(ω)E(ω) with the optical susceptibility

χ(ω)=−







ω + 

+ iγ

−

ω − 

+ iγ



. (2.22)

atomic optical susceptibility

2.2 Oscillator Strength

If we compare the atomic optical susceptibility, Eq. (2.22), with the result

of the oscillator model, Eq. (1.7), we see that both expressions have similar

structures. However, in comparison with the oscillator model the atom is

represented not by one but by many oscillators with diﬀerent transition

frequencies 

. To see this, we rewrite the expression (2.22), pulling out

the same factors which appear in the oscillator result, Eq. (1.7),

χ(ω)=







ω − 

+ iγ

−

ω + 

+ iγ



. (2.23)

Hence, each partial oscillator has the strength of





. (2.24)

oscillator strength

Here, we used |d

= e

. Adding the strengths of all oscillators by

summing over all the ﬁnal states n, we ﬁnd







n|x|ll|x|n(

− 

) . (2.25)

Using the Schrödinger equation H

|n = 

|n,wecanwrite

l|x|n(

− 



l|[x, H

]|n = −



l|[H

,x]|n , (2.26)

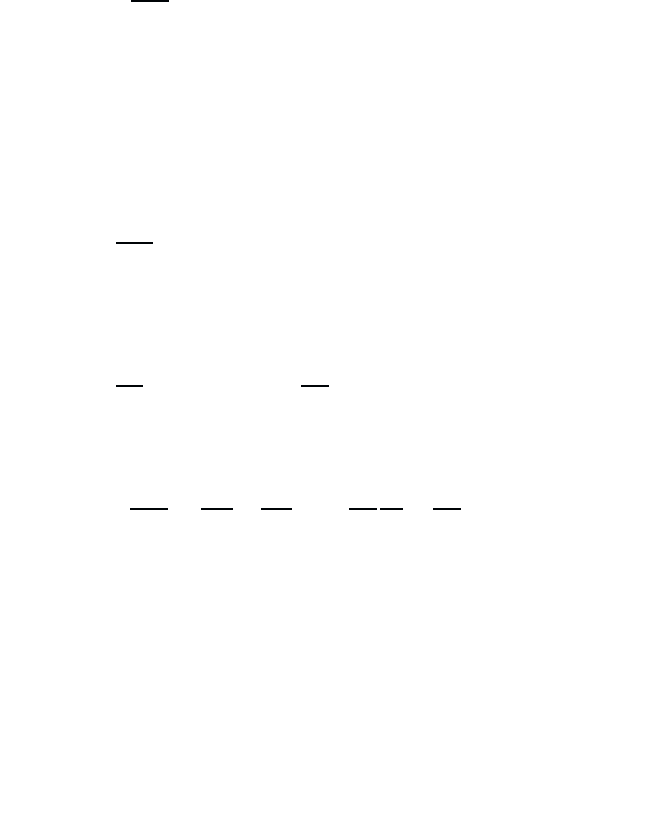
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

22 Quantum Theory of the Optical and Electronic Properties of Semiconductors

where [H

,x]=xH

−H

x is the commutator of x and H

. Inserting (2.26)

into (2.25) and using the completeness relation



|nn| =1we get



= −



l|[H

,x]x|l . (2.27)

Alternatively to (2.26), we can also manipulate the ﬁrst term in Eq. (2.25)

by writing

n|x|l(

− 

)=n|[H

,x]|l , (2.28)

so that





l|x[H

,x]|l . (2.29)

Adding Eqs. (2.27) and (2.29) and dividing by two shows that the sum over

the oscillator strength is given by a double commutator





l|[x, [H

,x]]|l =



l|[[x, H

],x]|l . (2.30)

The double commutator can be evaluated easily using

[x, H

]=−



−





i

(2.31)

and

,x]=−i (2.32)

to get



=1 . (2.33)

oscillator strength sum rule

Eq. (2.33) is the oscillator strength sum rule showing that the total tran-

sition strength in an atom can be viewed as that of one oscillator which is

distributed over many partial oscillators, each having the strength f

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Atoms in a Classical Light Field 23

Writing the imaginary part of the dielectric function of the atom as





(ω)=4πχ



(ω),usingχ(ω) from Eq. (2.23) and employing the Dirac

identity, Eq. (1.69), we obtain





(ω)=ω





[δ(ω − 

) − δ(ω − 

)] , (2.34)

with ω

=4πn

.Since|l is the occupied initial state and |n are

the ﬁnal states, we see that the ﬁrst term in Eq. (2.34) describes light

absorption. Energy conservation requires



= ω + 

, (2.35)

i.e., an optical transition from the lower state |l to the energetically higher

state |n takes place if the energy diﬀerence 

is equal to the energy ω

of a light quantum, called a photon. In other words, a photon is absorbed

and the atom is excited from the initial state |l to the ﬁnal state |n.This

interpretation of our result is the correct one, but to be fully appreciated it

actually requires also the quantum mechanical treatment of the light ﬁeld.

The second term on the RHS of Eq. (2.34) describes negative absorption

causing ampliﬁcation of the light ﬁeld, i.e., optical gain. This is the basis of

laser action. In order to produce optical gain, the system has to be prepared

in a state |l which has a higher energy than the ﬁnal state |n, because the

energy conservation expressed by the delta function in the second term on

the RHS of (2.34) requires



= ω + 

. (2.36)

If the energy of a light quantum equals the energy diﬀerence 

, stimulated

emission occurs. In order to obtain stimulated emission in a real system,

one has to invert the system so that it is initially in an excited state rather

than in the ground state.

2.3 Optical Stark Shift

Until now we have only calculated and discussed the linear response of an

atom to a weak light ﬁeld. For the case of two atomic levels interacting

with the light ﬁeld, we will now determine the response at arbitrary ﬁeld

intensities. Calling these two levels n =1, 2 with



>

, (2.37)

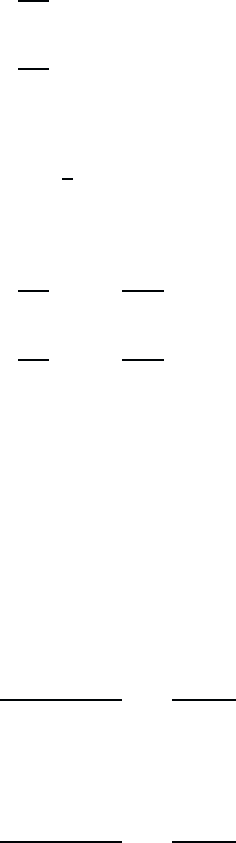
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

24 Quantum Theory of the Optical and Electronic Properties of Semiconductors

we get from Eq. (2.6) the following two coupled diﬀerential equations:

i

= −E(t)e

−i

, (2.38)

i

= −E(t)e

−i

, (2.39)

where we used d

=0. Assuming a simple monochromatic ﬁeld of the form

E(t)=

E(ω)(e

−iωt

+ c.c.) (2.40)

yields

i

= −d

E(ω)



−i(ω+

+ e

i(ω−



, (2.41)

i

= −d

E(ω)



−i(ω−

+ e

i(ω+



, (2.42)

where 

= −

has been employed. These two coupled diﬀerential equa-

tions are often called the optical Bloch equations. If we are interested only

in the light-induced changes around the resonance,

ω  

− 

, (2.43)

we see that the exponential factor exp[i(ω − 

)t] is almost time-

independent, whereas the second exponential exp[i(ω + 

)t] oscillates very

rapidly. If we keep both terms, we would ﬁnd that exp[i(ω −

)t] leads to

the resonant term proportional to

(ω − 

)+iγ

→ P

ω − 

− iπδ(ω − 

) (2.44)

in the susceptibility, whereas exp[i(ω + 

)t] leads to the nonresonant term

proportional to

(ω + 

)+iγ

→ P

ω + 

− iπδ(ω + 

) . (2.45)

For optical frequencies satisfying (2.43), the δ-function in (2.45) cannot be

satisﬁed since 

>

, and the principal value gives only a weak contribution

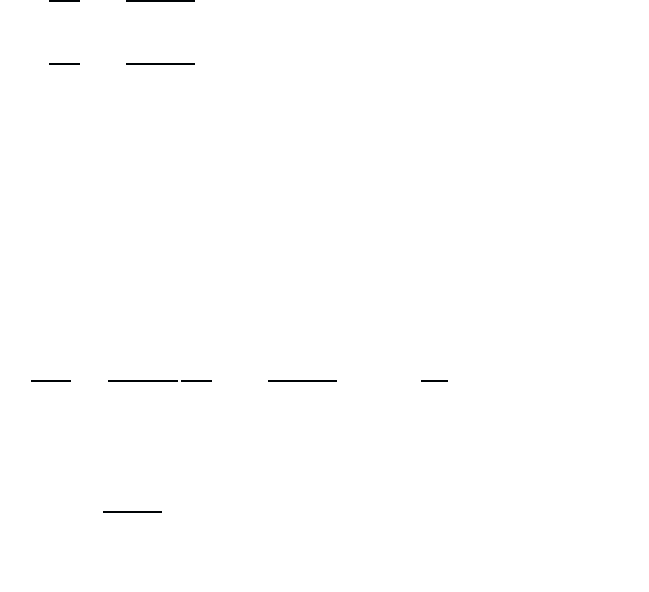
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Atoms in a Classical Light Field 25

to the real part. Hence, one often completely ignores the nonresonant parts

so that Eqs. (2.41) and (2.42) simplify to

i

= −

E(ω)

i(ω−

, (2.46)

i

= −

E(ω)

−i(ω−

. (2.47)

This approximation is also called the rotating wave approximation (RWA).

This name originates from the fact that the periodic time development

in Eqs. (2.46) and (2.47) can be represented as a rotation of the Bloch

vector (see Chap. 5). If one transforms these simpliﬁed Bloch equations

into a time frame which rotates with the frequency diﬀerence ω − 

,the

neglected term would be ω out of phase and more or less average to zero

for longer times.

To solve Eqs. (2.46) and (2.47), we ﬁrst treat the case of exact resonance,

ω = 

. Diﬀerentiating Eq. (2.47) and inserting (2.46) we get

= i

E(ω)

2

= −



E(ω)

2



= −

, (2.48)

whereweusedd

= d

∗

and introduced the Rabi frequency as



. (2.49)

Rabi frequency

The solution of (2.48) is of the form

(t)=a

(0)e

±iω

t/2

. (2.50)

For a

(t) we get the equivalent result. Inserting the solutions for a

and a

back into Eq. (2.5) yields

ψ(r,t)=a

(0)e

−i(

±ω

/2)t

(r)+a

(0)e

−i(

±ω

/2)t

(r) , (2.51)

showing that the original frequencies 

and 

have been changed to 

/2 and 

± ω

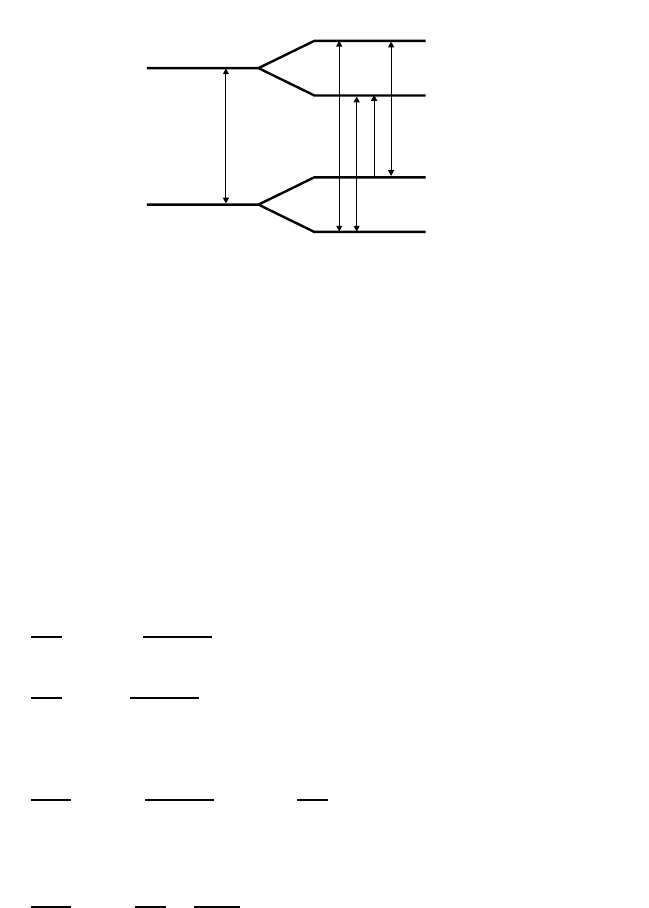
/2, respectively. Hence, as indicated in Fig. 2.1 one

has not just one but three optical transitions with the frequencies 

,and



± ω

, respectively. In other words, under the inﬂuence of the light

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

26 Quantum Theory of the Optical and Electronic Properties of Semiconductors

+2/

1 R

+2/

-2/

1 R

-2/

Fig. 2.1 Schematic drawing of the frequency scheme of a two-level system without

the light ﬁeld (left part of Figure) and light-ﬁeld induced level splitting (right part of

Figure) for the case of a resonant ﬁeld, i.e., zero detuning. The vertical arrows indicate

the possible optical transitions between the levels.

ﬁeld the single transition possible in two-level atom splits into a triplet,

the main transition at 

and the Rabi sidebands at 

± ω

. Eq. (2.49)

shows that the splitting is proportional to the product of ﬁeld strength and

electric dipole moment. Therefore, Rabi sidebands can only be observed

for reasonably strong ﬁelds, where the Rabi frequency is larger than the

line broadening, which is always present in real systems.

The two-level model can be solved also for the case of a ﬁnite detuning

ν = 

− ω. In this situation, Eqs. (2.46) and (2.47) can be written as

= ie

−iνt

E(ω)

2

(2.52)

= ie

iνt

E(ω)

2

. (2.53)

Taking the time derivative of Eq. (2.52)

= e

−iνt

E(ω)

2



ν + i



, (2.54)

and expressing a

and da

/dt in terms of a

we get

= −iν

−

(2.55)

with the solution

(t)=a

(0)e

iΩt

(or a

(t)=a

(0)e

−iΩt

) , (2.56)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Atoms in a Classical Light Field 27

where

Ω=−



+ ω

. (2.57)

Similarly, we obtain

(t)=a

(0)e

−iΩt

(or a

(t)=a

(0)e

iΩt

) . (2.58)

Hence, we again get split and shifted levels



→ Ω

≡ 

+Ω=

−



+ ω

(2.59)



→ Ω

≡ 

− Ω=



+ ω

. (2.60)

The coherent modiﬁcation of the atomic spectrum in the electric ﬁeld of a

light ﬁeld resembles the Stark splitting and shifting in a static electric ﬁeld.

It is therefore called optical Stark eﬀect. The modiﬁed or, as one also says,

the renormalized states of the atom in the intense light ﬁeld are those of

a dressed atom. While the optical Stark eﬀect has been well-known for a

long time in atoms, it has been seen relatively recently in semiconductors,

where the dephasing times are normally much shorter than in atoms, as

will be discussed in more detail in later chapters of this book.

REFERENCES

For the basic quantum mechanical theory used in this chapter we recom-

mend:

A.S. Davydov, Quantum Mechanics, Pergamon, New York (1965)

L.I. Schiﬀ, Quantum Mechanics,3rded., McGraw–Hill, New York (1968)

The optical properties of two-level atoms are treated extensively in:

L. Allen and J.H. Eberly, Optical Resonance and Two-Level Atoms, Wiley

and Sons, New York (1975)

P. Meystre and M. Sargent III, Elements of Quantum Optics, Springer,

Berlin (1990)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

28 Quantum Theory of the Optical and Electronic Properties of Semiconductors

M.SargentIII,M.O.Scully,andW.E.Lamb,Jr.,Laser Physics, Addison–

Wesley, Reading, MA (1974)

PROBLEMS

Problem 2.1: To describe the dielectric relaxation in a dielectric medium,

one often uses the Debye model where the polarization obeys the equation

= −

[P(t) − χ

E(t)] . (2.61)

Here, τ is the relaxation time and χ

is the static dielectric susceptibility.

The initial condition is

P(t = −∞)=0 .

Compute the optical susceptibility.

Problem 2.2: Compute the oscillator strength for the transitions between

the states of a quantum mechanical harmonic oscillator. Verify the sum

rule, Eq. (2.33).