Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Electroabsorption 369

E F (10 V/ )lectric ield cm

Exciton Peak Shiftme(V)

-10

-20

-30

with

without

xciton inding

orrection

Light Hole Exciton (lh)

Heavy Hole Exciton (hh)

}

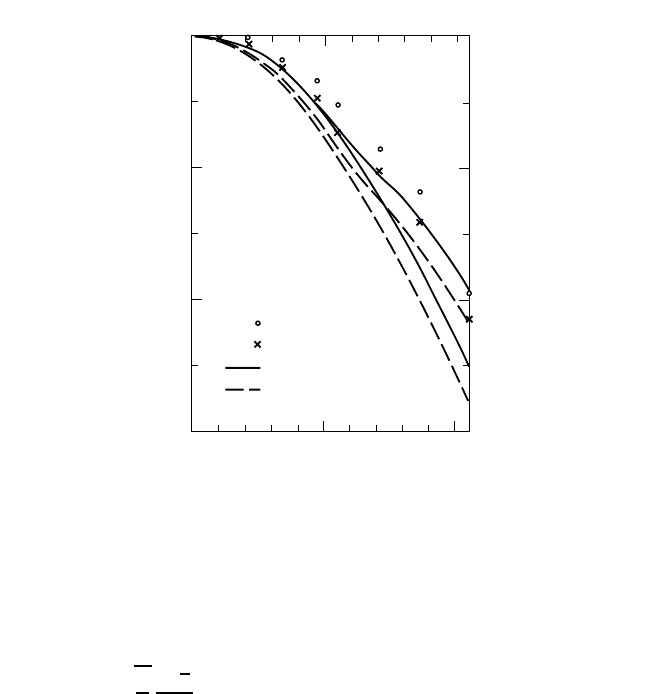
Fig. 18.6 Shift of the exciton peak position in a 95-Å multiple-quantum well as function

of the electric ﬁeld. [From Miller et al. (1985).]

For the wave function Ψ

(r),a1s-like function is assumed with a radius

λ, which is determined variationally

(r)=



−

. (18.96)

The total pair energy

= E

+ E

+ Ψ

∗

|Ψ (18.97)

is minimized with respect to λ for a given ﬁeld F. The resulting energy shifts

are shown in Fig. 18.6, together with the experimentally observed Stark

shifts for the heavy and light hole (hh and lh) exciton of a GaAs quantum

well with a width of 95 Å. One sees that Stark shifts up to 20 meV are

obtained with an electric ﬁeld of about 10

V/cm. Only above this large

value of the electric ﬁeld, ﬁeld-induced tunneling sets in and broadens the

exciton resonance. The quantum conﬁned Stark shift of  20meV is more

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

370 Quantum Theory of the Optical and Electronic Properties of Semiconductors

than twice the exciton binding energy of  9meV in this quantum well.

REFERENCES

M. Abramowitz and I.A. Stegun, Handbook of Mathematical Functions

(Dover Publ., 1972)

J.D. Dow and D. Redﬁeld, Phys. Rev. B1, 3358 (1970)

I.A. Merkulov and V.I. Perel, Phys. Lett. 45A, 83 (1973)

I.A. Merkulov, Sov. Phys. JETP 39, 1140 (1974)

D.A.B. Miller, D.S. Chemla, T.C. Damen, A.C. Gossard, W. Wiegmann,

T.H. Wood, and C.A. Burrus, Phys. Rev. B32, 1043 (1985)

S. Schmitt-Rink, D.S. Chemla, and D.A.B. Miller, Adv. in Phys. 38,89

(1989)

PROBLEMS

Problem 18.1: (a) Use ﬁrst-order perturbation theory in the applied ﬁeld

to evaluate the absorption spectrum, Eq. (18.42), for the quantum-conﬁned

Franz-Keldysh eﬀect. Use the basis functions (18.41) to show the reduction

in oscillator strength for the transition between the lowest electron–hole

subband, 0, h → 0, e. This transition is fully allowed without ﬁeld, and it

is reduced in the presence of the ﬁeld. (b) Use the same method as in (a)

to show that the ﬁeld makes the transition 0, h → 1e dipole allowed.

Problem 18.2: Show that the tunnel integral, ﬁrst term of Eq. (18.88),

can be transformed into the expression

= F

1/2



√



− z)(z − z

) (18.98)

and further into the form



3/2



−1



1 − t

1+st



3/2

I(s) , (18.99)

where s =



1 −





1 − y

Problem 18.3: Show that the evaluation of the integral I(s), deﬁned in

Eq. (18.99), for s =1gives the Franz-Keldysh result I(1) =

√

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Chapter 19

Magneto-Optics

The application of magnetic ﬁelds in solid state physics and particularly also

in semiconductor optics has always been an extremely versatile tool, partic-

ularly for the identiﬁcation of the symmetry of electronic states. Therefore,

magneto-optics has become a very large ﬁeld in its own right. In this chap-

ter, we discuss only some basic aspects of the inﬂuence of the magnetic ﬁelds

on the free electron motion, which are of particular interest for the intrinsic

linear and nonlinear optical properties of semiconductors and semiconduc-

tor microstructures. We focus on the optical properties of magneto-excitons

and magneto-plasmas in quantum conﬁned structures.

The Lorentz force of a constant magnetic ﬁeld constrains a free electron

on a cyclotron orbit perpendicular to the magnetic ﬁeld. An especially well-

deﬁned problem arises, if one applies a magnetic ﬁeld perpendicularly to a

quantum well which suppresses the electron motion in the ﬁeld direction. In

this conﬁguration, interesting physical phenomena, such as the quantized

Hall eﬀect and the crystallization of the electrons into a Wigner crystal

occur.

It has been shown that the Hartree-Fock theory becomes exact for a two-

dimensional electron gas in the limit of low temperatures and high magnetic

ﬁelds. Therefore, we limit our discussion in this chapter to the Hartree-Fock

theory of magneto-excitons and magneto-plasmas in 2D quantum wells and

1D quantum wires. Modeling the wire conﬁguration as an additional weak

harmonic lateral conﬁnement allows us to study the smooth transition be-

tween eﬀectively 1D and 2D systems. In this treatment, we follow the

theoretical work presented in Bayer et al. (1997) and show a comparison

with experimental results.

First, we discuss the single-particle problem, which can be treated ex-

actly for a harmonic lateral conﬁnement potential in terms of modiﬁed

371

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

372 Quantum Theory of the Optical and Electronic Properties of Semiconductors

Landau eigenfunctions. Expanding the density matrix in the Landau basis,

we derive the Bloch equations of the magneto-plasma. Only the Coulomb

exchange terms are kept. Assuming quasi-equilibrium carrier distributions,

we then use the polarization equation to calculate the linear absorption,

gain and luminescence spectra, which can be compared most directly to

experimental observations in quantum wires.

19.1 Single Electron in a Magnetic Field

We consider an electron in a quantum well (x − y plane) that experiences

an additional smooth lateral quantum-wire conﬁnement potential in the x-

direction. The electron moves under the inﬂuence of a constant magnetic

ﬁeld in the z-direction. For realistic quantum wires, the conﬁnement po-

tential can be assumed to have a Gaussian shape, which for the lower-lying

states can be approximated by a harmonic oscillator potential.

We assume the validity of the eﬀective mass approximation and neglect

all band-mixing eﬀects taking into account only those states that are formed

out of the lowest quantum-well electron and heavy-hole subbands. The

single-particle Hamiltonian for an electron (j = e)orahole(j = h)moving

in the x − y plane with the wire axis in the y directioncanbewrittenas



− e

A(r

)]

Ω

. (19.1)

Here, the band gap E

of the underlying quantum well is split symmetrically

between the electrons (−|e|) and holes (|e|). The term

Ω

models the

lateral conﬁnement potential characterized by the intersubband frequencies

Ω

The vector potential A describes the constant magnetic ﬁeld B = e

in z-direction. The vector potential is not uniquely deﬁned. Two gauges

are commonly used:

(i) the symmetric gauge with

A(r)=

B × r =

(−ye

+ xe

) , (19.2)

(ii) the asymmetric Landau gauge

A(r)=xBe

. (19.3)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Magneto-Optics 373

One can easily verify that in both cases

B = curl A =



∂/∂x ∂/∂



= B e

. (19.4)

For practical purposes, it is often advantageous to use the asymmetric Lan-

dau gauge (ii) which depends only on the x-coordinate. In this frame, the

magnetic ﬁeld produces together with the conﬁnement potential (charac-

terized by the oscillator frequency Ω

) a harmonic oscillator potential in

the x-direction, while one has a free motion in the y-direction.

In the Landau gauge, the single-particle Hamiltonian (19.1) can be writ-

ten as



− e

)]

Ω

(19.5)

=−



∂

∂x

−



∂

∂y

− ω

c,j

∂

∂y

(Ω

+ω

c,j

where

c,j

(19.6)

cyclotron frequency

is the cyclotron frequency of the carriers j.

For the total wave function, we make the ansatz

iky



) , (19.7)

where the plane wave contribution results from the absence of a conﬁning

potential in y-direction. Inserting this ansatz into Schrödinger’s equation

and using a quadratic completion, we obtain the x-dependent Hamiltonian

)=−



∂

∂x

eff,j

− ∆x

)



eff,j

. (19.8)

Here, the eﬀective oscillator frequency is given by

eff,j



Ω

+ ω

c,j

. (19.9)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

374 Quantum Theory of the Optical and Electronic Properties of Semiconductors

The origin of the oscillator potential is shifted by

∆x

= kδ

= k



c,j

eff,j

. (19.10)

Furthermore, we introduced the translational eﬀective mass for the

quantum-wire electron in a magnetic ﬁeld

eff,j

= m



eff,j

Ω



. (19.11)

This eﬀective mass increases quadratically with the magnetic ﬁeld once

the cyclotron frequency exceeds the spectral diﬀerence between the wire

subbands. Writing the oscillator potential term in the Hamiltonian (19.8)



eff,j

− kδ

)

− kδ

)

eff,j

)

, (19.12)

we identify the characteristic length

eff,j





eff,j

, (19.13)

which is the amplitude of the electron’s zero point ﬂuctuations. This

length is a generalization of the so-called Landau length, which deter-

mines the cyclotron radius. With l

eff,i

,theshift∆x

becomes ∆x

eff,i

(ω

c,i

/ω

eff,i

). It is interesting to note that this shift of the origin

depends on the momentum along the wire. This can be understood as the

action of the Lorentz force on the moving carrier.

The eigenfunctions of (19.8) are shifted harmonic oscillator functions

− ∆x

), also called modiﬁed Landau states. Hence, the complete

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Magneto-Optics 375

single-particle eigenfunctions are

k,ν

iky

√

)

iky

√

−∆x

) with ν =0, 1, 2, ··· . (19.14)

modiﬁed Landau eigenfunctions

The corresponding single-particle energies are

k,ν



ef f,j

+ ω

ef f,j



ν +



. (19.15)

modiﬁed Landau ladder

The eﬀective mass increases with increasing magnetic ﬁeld showing how the

ﬁeld hinders the translational motion along the wire. The characteristic

frequency of the Landau ladder with parabolic conﬁnement potential and

magnetic ﬁeld is ω

eff,j



Ω

+ ω

c,j

. Thus, the magnetic ﬁeld increases

the lateral subband spacing.

Finally, we note that the electron and hole wave functions are the time-

reversal counterparts of each other

k,ν

−k,ν

∗

. (19.16)

19.2 Bloch Equations for a Magneto-Plasma

In order to study the optical properties of the quantum conﬁned magneto-

plasma, we derive the Bloch equations for this system by expanding the

electron–hole density matrix into the modiﬁed Landau base (19.14), which

diagonalizes the single-particle problem. The Coulomb interactions between

the optically excited carriers are taken into account in the mean-ﬁeld ap-

proximation. As mentioned above, this approximation becomes very good

for strong eﬀective quantum conﬁnement through the combined inﬂuence

of barriers and magnetic ﬁeld.

For simplicity, we analyze a conﬁguration with equal eﬀective electron

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

376 Quantum Theory of the Optical and Electronic Properties of Semiconductors

and hole masses, so that

Ω

= m

Ω

= mΩ , (19.17)

where Ω is the total inter-subband spacing. This approximation assures

local charge neutrality. While the values of the axial momentum k are

unrestricted for B =0, they are restricted in the presence of a magnetic

ﬁeld by the condition that the center of the carrier wave function ∆

x must

lie inside the quantum wire. This condition imposes

∆x

= kδ

≤

(19.18)

as condition for the harmonic conﬁnement potential.

If we ﬁt the lateral subband splitting Ω with the energy splitting between

the two lowest subbands of a rectangular square well

Ω=



2π





−







3π



2mL

(19.19)

we obtain for the largest allowed wave number k

3π

eff

Ω

= κ

. (19.20)

Here, ω

and ω

eff

are also calculated with the reduced mass m.Nowthe

density of states can be calculated:

D(E)=trδ(E −H)=



ν,k

δ(E − E

k,ν

)

2π



−κ





eff

+ E

k=0,ν

− E



2π



−κ

dκ





−

E − E

k=0,ν



, (19.21)

where we used Eq. (4.6) for D =1with ∆k =

2π

.Furthermore,we

introduced κ = kL

as integration variable and

= 

/(2m

eff

) as

characteristic energy. The integral over the delta function yields

D(E)=

2π





−

E − E

k=0,ν





E − E

k=0,ν

. (19.22)

With increasing magnetic ﬁeld the single-particle density of states changes

from the 1/

√

E-like behavior of a 1D system to the δ-function-like behavior

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Magneto-Optics 377

of a totally conﬁned system. Calculating now the total number of states g

in a quasi-1D subband with index ν, one ﬁnds the relation

g ∝

eff

Ω

. (19.23)

In contrast to a quantum well in a normal magnetic ﬁeld, for which the

number of states in a Landau level depends linearly on the magnetic ﬁeld,

the number of states in a quantum wire is nearly constant for weak ﬁelds,

and approaches the linear dependence only in the high-ﬁeld limit.

The matrix elements of the Coulomb potential (see also Problem 19.2)

can be written as

j,j



ν,ν



;ν



,ν

(q)=



2πe











dxφ

∗

(x+δq)e



(x)



= V

j,j



ν,ν



(19.24)

where 

is the background dielectric function. Using the modiﬁed Landau

states (19.14), one can evaluate the Coulomb matrix elements analytically

in terms of modiﬁed Bessel functions of zeroth and ﬁrst order (see the

evaluations in Wu and Haug). As deﬁned in Sec. 12.2, the single-particle

density matrix is

i,ν;i



,ν

(k, t)=a

†

i,k,ν

(t)a



,k,ν

(t) , where {i, i



} = {c, v} . (19.25)

Here, we consider only diagonal elements in ν because the optical transitions

in our model connect only states with the same Landau subband quantum

number. Switching to the electron–hole representation, the relevant carrier

densities are

ν,ν

(k)=α

†

k,ν

 = n

k,ν

(19.26)

and

ν,ν

(k)=β

†

k,ν

 = n

k,ν

, (19.27)

with the electron and hole operators α,α

†

and β, β

†

, respectively. Following

the derivation in Chap. 12, we ﬁnd for the optical interband polarization

ν,ν

(k, t)=β

−k,ν

k,ν

 = P

k,ν

(19.28)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

378 Quantum Theory of the Optical and Electronic Properties of Semiconductors

the dynamic equation



∂

∂t

− e

k,ν

− e

k,ν



k,ν

+ n

k,ν

− 1

R,k,ν

(t)+i

∂P

k,ν

∂t



scatt

(19.29)

Here, the carrier energies e

k,ν

are the exchange renormalized single-particle

energies

e

k,ν

= E

k,ν

−



q,ν



ν,ν



(q)n



k−q,ν



(t) , (19.30)

with the Landau ladder energies E

k,ν

(19.15). The sum j



extends only

over the Landau subbands of the considered species.

The exchange renormalized Rabi frequency ω

is given by

ω

R,k,ν

(t)=d

E(t)+



q,ν



ν,ν



(q)P

k−q,ν



. (19.31)

The equations for the carrier densities are

∂

∂t

k,ν

= −2Im



R,k,ν

(t)P

∗

k,ν



∂n

k,ν

∂t



scatt

, (19.32)

copmpare Eqs. (12.19).

Because in quantum wires the luminescence emerging from the end of

the wires can be measured most easily, we limit our analysis to the calcula-

tion of the wire luminescence. In the experiments, the carriers are excited

by a a cw pump ﬁeld and have enough time to thermalize before their radia-

tive decay. Therefore, we have to calculate only the polarization equation

with quasi-equilibrium Fermi distributions of the carriers. The density and

the temperature of the carrier distributions are used as ﬁtting parameters

in the comparison with corresponding measured spectra.

19.3 Magneto-Luminescence of Quantum Wires

In this section, we follow the procedure discussed in Chap. 15 to com-

pute the quasi-equilibrium optical nonlinearities. We slightly generalize the

treatment by including the summations over the Landau subband states.

Again, we start by calculating the stationary optical interband polar-

ization components which are linear in the ﬁeld E(t)=E

−iωt

.Thesta-