Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 359
where I
eh
is again the square of the normalized overlap integral between
the electron and hole wave functions
I
eh
=
+L/2
−L/2
dz ψ
n
e
(z)ψ
n
h
(z)
2
A
n
e
A
n
h
. (18.49)
Fig. 18.2 shows the calculated wave functions in the potential well with and
without an electric field. The picture of the wave functions gives immedi-
ately the information how the overlap integral I
eh
changes due to the field
for the various inter-subband transitions.
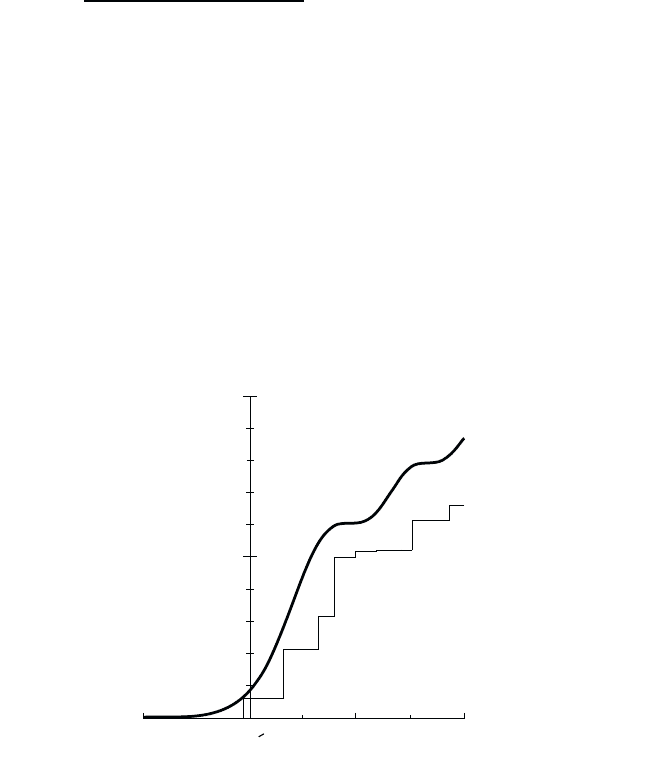
In Fig. 18.3, we plot the calculated absorption spectrum for a GaAs
quantum well with L= 150 Å width in the presence of an electric field of
10
5
Vcm
−1
. We see, e.g., that the transition between the second valence
subband and the first conduction subband, which was forbidden without
field, obtains a large oscillator strength in the field. For the limit L →∞,
the inter-subband transitions approach the modulation of the bulk Franz-
Keldysh spectrum.
-100
0
100
200
(1.1)
10
20
(2.1)
(3.1)
(1.2)
(4.1)
(2.2)
(5.1)
(3.2)
(4.2)
Absorption (a. u.)
h -E [meV]w
g
Fig. 18.3 Calculated absorption of a 150 Å thick GaAs-like quantum well at 10
5
Vcm
−1
.
The individual transitions are labeled (n
v
,n
c
) where n
v
(n
c
) is the valence (conduction)
subband number. The smooth line is the calculated Franz-Keldysh effect for bulk mate-
rial, see Fig. 18.1. [After Schmitt-Rink et al. (1989).]

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
360 Quantum Theory of the Optical and Electronic Properties of Semiconductors
18.3 Exciton Electroabsorption
In this section, we extend the treatment to include the attractive electron–
hole Coulomb potential. Instead of Eq. (18.3), we then have to solve the
basic pair equation
−
2
∆
2m
r
− ezF −
e
2
0
r
− E
µ
ψ
µ
=0 . (18.50)
Again, we discuss the solution of this equation and the resulting optical
spectra both for bulk and quantum-well semiconductors.
18.3.1 Bulk Semiconductors
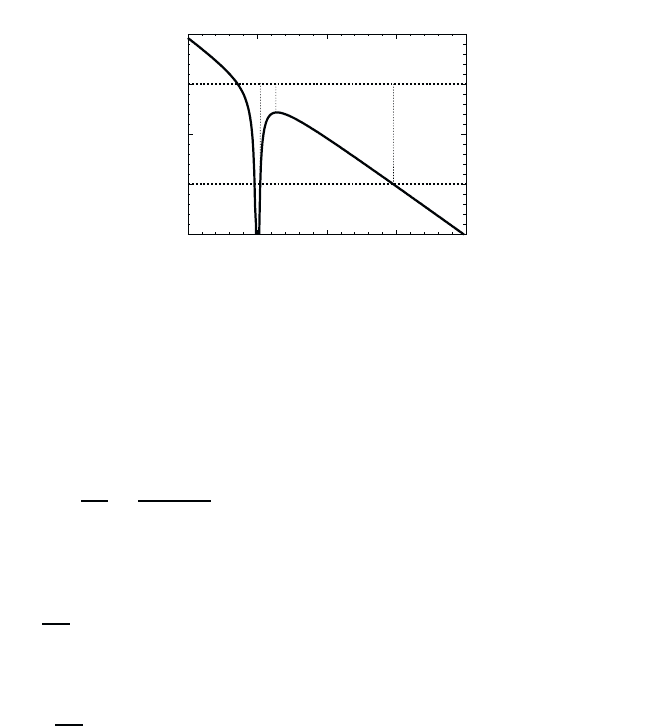
The exciton in a bulk semiconductor loses its stability in the presence of
an electric field, as can be seen easily by inspecting the total electron–
hole potential in Eq. (18.50). Plotting this potential along the z direction,
Fig. 18.4, we see immediately that the exciton can be ionized if one of the
carriers tunnel from z
1
to z
2
through the potential barrier. The tunne-
ling causes a lifetime broadening of the exciton resonance. For example,
for GaAs the exciton resonance vanishes completely for fields larger than
10
3
V/cm. In addition to the broadening, there is also a shift of the exciton
resonance, the so-called (dc) Stark shift. Second-order perturbation shows
immediately that the shift of the ground state is quadratic in the field and
negative
∆E
0
−
(ea
0
F )
2
E
0
≡−F
2
E
0
, (18.51)
which holds as long as the perturbation is sufficiently small, i.e., F << 1.
But still more interesting is the question how the Franz-Keldysh absorption
tail will be modified by excitonic effects. To study the region of the exciton
absorption tail, we use the quasi-classical approximation introduced into
quantum mechanics by Wentzel, Kramers and Brillouin, and often called
the WKB method. This approach has been applied by Dow and Redfield
(1970) to the present problem, we follow here the analytical approximations
by Merkulov and Perel (1973) and Merkulov (1974).
In excitonic units, Eq. (18.50) becomes
∆+Fz +
2
r
−
ψ =0 , (18.52)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 361
-1.5
-1
-0.5
0
0.5
-50
0 50 100 150
V/E
0
z/a
0
z
1
z
3
z
2
Fig. 18.4 Exciton potential in z-direction with an applied electric field (F =0.01).
where all coordinates are scaled with the Bohr radius and all energies with
the exciton Rydberg energy, respectively. Since the scaled pair energy is
always negative in the tail region, we introduced the positive energy scale
≡−
E
µ
E
0
≡
E
g
− ω
E
0
> 1 . (18.53)
Here, the energy ω of the exciting photon is assumed to be below the
band-gap energy, so that is always positive and larger than unity.
The maximum of the potential (point z
3
in Fig. 18.4) has an energy of
−2
√
2F in z direction. For simplicity, we assume that the applied field is
not too strong so that we always have potential barrier even for the lowest
exciton state, i.e.,
2
√
2F <
min
=1 . (18.54)
Under this condition, the exciton still exists as a quasi-bound state and we
can essentially divide the solution of the problem into three steps: i) For
the regime far away from the center of the exciton, we make a quasiclassical
approximation and use as formal expansion parameter. ii) For z<z
1
, i.e.,
inside the Coulomb well, we neglect the electric field in comparison to the
Coulomb potential and use the quantum mechanical solution (Chap. 10) for
the exciton problem. iii) We match the solutions in the regime z
1
<z<z
3
,
where the quasiclassical approximation is still reasonably good and where
the electric field is still small in comparison to the Coulomb potential.
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
362 Quantum Theory of the Optical and Electronic Properties of Semiconductors
First, we derive the quasiclassical solution for z>z
2
. In cylindrical
coordinates, the Laplace differential operator is given by
∆=
1
ρ
∂
∂ρ
ρ
∂
∂ρ
+
∂
2
∂z
2
+
1
ρ
2
∂
2
∂φ
2
, (18.55)
where ρ is the radius perpendicular to z. Because only the wave functions
with the angular-momentum quantum number m =0are finite in the origin
and thus contribute to the absorption spectrum, we drop the dependence
on the angle φ,
1
ρ
∂
∂ρ
ρ
∂
∂ρ
+
∂
2
∂z
2
+ Fz +
2
ρ
2
+ z
2
−
ψ
sc
=0 . (18.56)
The force K linked with the potential
V (ρ, z)=−Fz − 2/
ρ
2
+ z
2
(18.57)
is given as
K = −∇V = Fe
z
−
2ze
z
+2ρe
ρ
r
3
, (18.58)
where e
z
and e
ρ
are the unit vectors in z and ρ direction, respectively. The
ratio of the two force components
K
ρ
K
z
= −
2ρ
Fr
3
− 2z
(18.59)
is always small for r
2
>> F
−1
. At the maximum of the potential barrier
z
2
3
=
2
F
,
so that one can approximately neglect K
ρ
in the region z>z
3
.Itis
therefore a good approximation in the whole quasiclassical region to use
only a one-dimensional potential
V (z)=−Fz −
2
z
(18.60)
instead of the full potential, Eq. (18.57). In this case, Eq. (18.56) simplifies
to
1
ρ
∂
∂ρ
ρ
∂
∂ρ
+
∂
2
∂z
2
− V (z) −
ψ
sc
=0 . (18.61)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 363
Using the ansatz
ψ
sc
(ρ, z)=χ(ρ)Ψ(z) , (18.62)
we can separate Eq. (18.61) into
1
ρ
∂
∂ρ
ρ
∂
∂ρ
+ p
2
ρ
χ =0 (18.63)
and
∂
2
∂z
2
− V (z) − − p
2
ρ
Ψ=0 , (18.64)
where p
ρ
is the quasimomentum perpendicular to the z-axis.
Eq. (18.63) is a version of Bessel’s differential equation and the solutions
are the cylindrical Bessel functions
χ(ρ)=J
0
(p
ρ
ρ) . (18.65)
To solve Eq. (18.64), we make the quasiclassical approximation. For
this purpose, we introduce again formally the -dependence of the kinetic
energy operator, use as a formal expansion parameter, and put it equal
to unity at the end. We write Eq. (18.64) as
2
∂
2
∂z
2
+ p
2
(z)
Ψ=0 , (18.66)
whereweintroducethequasimomentump(z) through the relation
p
2
(z)=− − V (z) − p
2
ρ
. (18.67)
Inserting the ansatz
Ψ(z)=e
i
σ(z)
(18.68)
into Eq. (18.66) results in
iσ
− (σ
)
2
+ p
2
=0 . (18.69)
Now, we expand the phase function σ(z) formally in powers of /i
σ(z)=σ
0
(z)+(/i)σ
1
(z)+(/i)
2
σ
2
(z)+··· (18.70)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
364 Quantum Theory of the Optical and Electronic Properties of Semiconductors
and compare the various orders of . In the order O(
0
),weobtain
σ
0
(z)=±p(z) , (18.71)
with the solution
σ
0
(z)=±
z
z
2
dζ p(ζ) . (18.72)
The first-order equation is
iσ
0
+2iσ
0
σ
1
=0 , (18.73)
so that
σ
1
(z)=−ln
p(z)+ln C, (18.74)
where ln C is a normalization constant. Summarizing the results, we obtain
Ψ(z)=
C
|p(z)|
exp
±i
z
z
2
dζ p(ζ)
, (18.75)
where we put the formal expansion parameter → 1.
Because a classical particle cannot penetrate into regions in which the
potential energy exceeds the total energy, we define the classical turning
points by p
2
(z
1,2
)=0and find
z
2,1
=
1
2F
( + p
2
ρ
) ±
( + p
2
ρ
)
2
− 8F
. (18.76)
The quasimomentum p(z) is real in the region, z>z
2
and the wave function
(18.75) describes oscillatory solutions.
In the region of the potential barrier, z
1
<z<z
2
,>1 and −V (z) < 1,
so that p
2
(z) < 0 and p(z) is purely imaginary. Eq. (18.75) describes an
exponentially increasing or decaying solution in the classically forbidden
region. The exponentially increasing solution is clearly unphysical and has
to be discarded, so that we have in the classically forbidden region
Ψ(z)=
C
|p(z)|
exp
−
z
z
2
dζ |p(ζ)|
. (18.77)
Now, we can approximate
|p(z)| =
+ V (z)+p
2
ρ
p
0
(z)+
p
2
ρ
2p
0
(z)
(18.78)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 365
with p
0
(z)=[ + V (z)]
1/2
and the integral in Eq. (18.77) can be simplified
by considering that z deviates only slightly from r, i.e.,
z = r cos(θ) r
1 −
1
2
θ
2
, (18.79)
so that
Ψ(z)
C
|p(z)|
exp
r
z
2
dζ
p
0
+
p
2
ρ
2p
0
+
z
r
dζ p
0
C
|p(z)|
exp
−
z
2
r
dζ
p
0
+
p
2
ρ
2p
0
exp
−
rθ
2
2
√
. (18.80)
Here, z
2
can be evaluated for p
ρ
0. Furthermore, in the vicinity of
the z-axis the argument of the Bessel function can be put equal to zero
J
0
(p
ρ
ρ) J
0
(0) = 1, so that the semiclassical form of the wave function
(18.62) becomes ψ
sc
=Ψ.
Now, we turn to the solution of the exciton problem for the core region,
z<z
3
, in which we may neglect approximately the field. Using Eq. (10.70),
we may write the exciton wave functions with l =0and m =0,whichare
finite at the origin, as
Ψ
x
(r)=Ψ(0)e
−r
√
F
1 −
1
√
;2;2
√
r
, (18.81)
whereweusedtherelations
L
2l+1
n+l
2r
na
0
=
(n + l)!(n + l)!
(n − l − 1)!(2l +1)!
F
−n + l +1;2l +2;
2r
na
0
(18.82)
and
n =
E
0
E
n
=
1
√
. (18.83)
For r>>
−1/2
, one may use the asymptotic form of the confluent hyper-
geometric function,
F (a; b; z) →
e
z
Γ(b)z
a−b
Γ(a)
(18.84)
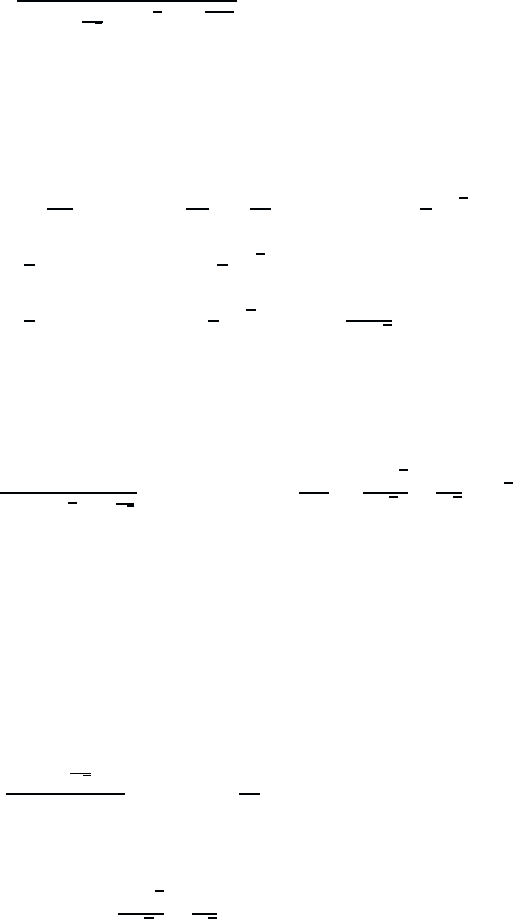
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
366 Quantum Theory of the Optical and Electronic Properties of Semiconductors
which yields
Ψ
x
(r)=
Ψ(0) exp[(−r
1/2
)]
Γ
$
1 −
1
√
%
(2
√
r)
1+
1
*
1/2
. (18.85)
This function has to be matched with the spherical part of the semiclassical
wave function (18.80) which is obtained by averaging the angle-dependent
part of (18.80) over the angles
¯
Ψ
sc
(r)=
dΩ
4π
Ψ(r)=
2π
0
dφ
2π
π
0
dθ
2
sin θf(r)exp
−
1
2
r
√
θ
2
1
2
π
0
dθθf(r)exp
−
1
2
r
√
θ
2
1
4
∞
0
dxf(r)exp
−
1
2
r
√
x
= f (r)
1
2r
√
,
where f (r) stands for the angle-independent parts. The total spherical part
of the semiclassical wave function can therefore be written as
¯
Ψ
sc
(r)
C
1/4
(2
√
r)
1+
1
√
*
exp
−
z
2
z
1
dζ
p
0
+
p
2
ρ
2p
0
−
ln
√
√
−
1
√
−
√
r
.
(18.86)
Here, we introduced the tunnel integral ranging from z
1
to z
2
.Thein-
tegral from z
1
to r has been evaluated approximately. The semiclassical
wave function
¯
Ψ
sc
, Eq. (18.86), and the asymptotic exciton wave function
Ψ
x
, Eq. (18.85), have approximately the same r-dependence. We used
−1/2
ln 2r
−1/2
, which holds approximately for the matching region. A
comparison of the coefficients yields
ψ(0) =
Γ
$
1 −
1
√
%
C
1/4
exp
−T
t
−
p
2
ρ
2
α
t
, (18.87)
where
T
t
=
z
2
z
1
dζ p
0
(ζ)+
ln
√
√
+
1
√
(18.88)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 367
and
α
t
=
z
2
z
1
dζ
1
p
0
(ζ)
. (18.89)
The α
t
correction term becomes unimportant, because the summation over
all p
ρ
values brings the correction down from the exponent, so that it enters
into the result as an unimportant prefactor. The evaluation of the tunnel
integral yields
T
t
=
2
2/3
3F
−
1
√
ln
8
3/2
F
. (18.90)
The first term in Eq. (18.90) gives rise to the Franz-Keldysh result, while the
second term describes the quite significant modification due to the Coulomb
potential. The only unknown coefficient in the result is the normalization
constant C. The existence of the exciton has little influence on the normal-
ization which is determined by the asymptotic form of the wave function,
see Chap. 10. Thus the normalization is the same as for free carriers.
The resulting absorption spectrum is
α(ω)=α
FK
(ω)
,
Γ
1 −
1
√
exp
1
√
ln
8
3/2
F
-
2
, (18.91)
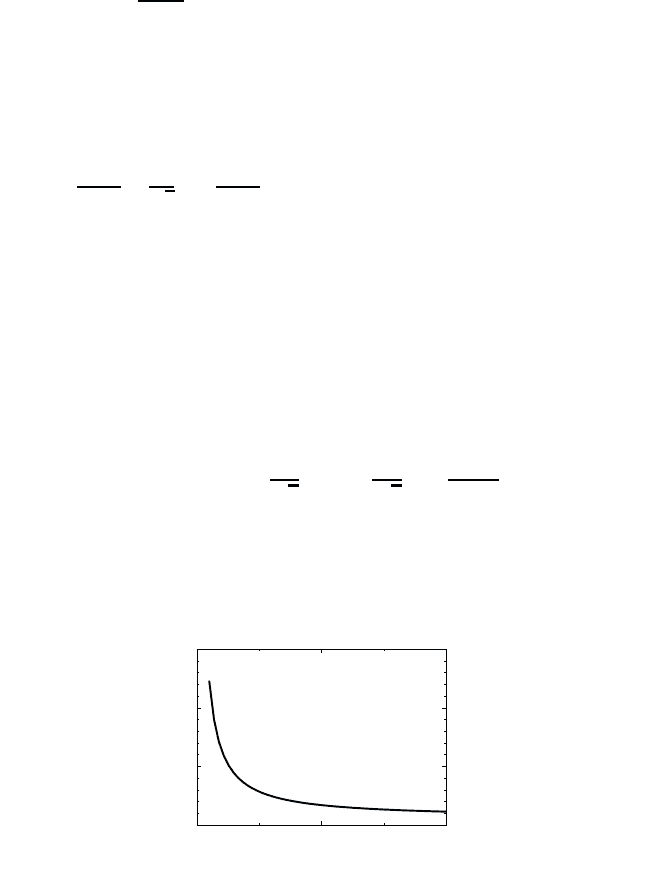
bulk exciton electroabsorption
0
100
200
300
1
2 3
a
e
Fig. 18.5 Exciton enhancement of the electroabsorption according to Eq. (18.91). α is
in units of α
FK
and =(E
g
− ω)/E
0
.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
368 Quantum Theory of the Optical and Electronic Properties of Semiconductors
where =(E
g
− ω)/E
0
and α
FK
(ω) is the Franz-Keldysh absorption
coefficient given in Eq. (18.33). An example of the absorption spectrum
according to Eq. (18.91) is shown in Fig. 18.5. Depending on the detuning
and the field strength F, the exciton electroabsorption coefficient can be
up to 10
3
times larger than the Franz-Keldysh absorption coefficient. The
absorption approaches the Franz-Keldysh spectrum asymptotically only for
very large detunings.
18.3.2 Quantum Wells
The spatial confinement in a quantum well prevents field ionization of the
exciton up to very large field strengths. As a consequence, one can ob-
serve very large Stark shifts of, e.g., the lowest exciton resonance in a field
perpendicular to the layer of the quantum well (Miller et al., 1985).
In order to treat the problem, we decompose it into that of the one-
dimensional motion of the noninteracting electron and hole in the quantum-
well potential V
i
(z
i
) and the field, and into that of the relative electron–hole
motion in the layer under the influence of the Coulomb interaction. We
write the total Hamiltonian as
H = H
ez
+ H
hz
+ H
eh
, (18.92)
where
H
iz
= −
2
2m
i
∂
2
∂z
2
i
+ V
i
(z
i
) ± eEz
i
,i= e, h (18.93)
and
H
eh
= −
2
2m
∂
2
∂r
2
−
e
2
0
r
2
+(z
e
− z
h
)
2
. (18.94)
For the wave function, we use a product ansatz
ψ = ψ
e
(z
e
)ψ
h
(z
h
)Ψ
eh
(r) , (18.95)
where the wave functions ψ
i
(z
i
) are the eigenfunctions of the Hamiltonian
(18.93). Assuming infinitely high potential wells, the functions ψ
i
(z
i
) are
given by Eq. (18.44) in terms of Airy functions. The effect of a finite poten-
tial well and the resulting leaking of the wave functions into the embedding
material can approximately be accounted for by introducing an effective
well width L
eff
which is slightly larger than the actual width L.
