Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Chapter 18
Electroabsorption
An important tool in solid-state spectroscopy is the application of static
electric or magnetic fields. These fields give rise to characteristic changes
in the optical spectra yielding valuable information about the nature of the
optical transitions. In this chapter, we discuss the effects of dc-electric fields
on the absorption of bulk (3D) and quantum-well (quasi-2D) semiconduc-
tors showing that the field effects in the respective absorption spectra are
remarkably different.
Applying an electric field to atomic systems causes a reduction of the
overall symmetry, which leads to the splitting of degenerate levels and to
field-dependent level shifts. This effect is called the (dc) Stark effect. If one
applies an external electric field to a semiconductor, this field has a pro-
nounced influence on the optically active electron–hole pairs. In comparison
to these effects, it is often justified to disregard field-induced changes in the
atomic orbits. Following this philosophy, we therefore describe the atomic
orbits by the unperturbed Bloch functions and study the influence of the
field on the relative motion of the electron–hole pair using effective mass
approximation.
18.1 Bulk Semiconductors
In Chap. 10, we compute the semiconductor band-edge absorption spectrum
for directly allowed optical transitions. The result can be written as
α(ω)=α
b
n
|ψ
n
(r =0)|
2
δ(E
n
− ω) , (18.1)
349
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
350 Quantum Theory of the Optical and Electronic Properties of Semiconductors
where
α
b
=
8π
2
|d
cv
|
2
ω
n
b
c
, (18.2)
including a factor 2 from the spin summation. In Eq. (18.1), ψ
n
and E
n
are the eigenfunctions and energy eigenvalues of the electron–hole pair,
respectively, where E
n
includes the band-gap energy E
g
.
If we disregard the Coulomb effects altogether, the stationary
Schrödinger equation of the relative motion of the electron–hole pair in
the presence of an electric field F (parallel to the z-axis) can be written as
−
2
∆
2m
r
− ezF − E
n
ψ
n
(r)=0 . (18.3)
To solve this equation, we make the ansatz
ψ
n
(r)=
1
L
e
i(k
x
x+k
y
y)
ψ
n
(z) , (18.4)
where L = V
1/3
is the linear extension of the system. We write the energy
eigenvalue as
E
n
=
2
2m
r
(k
2
||
+ κ
2
n
) ≡ E
n,k
||
, (18.5)
with k
2
||
= k
2
x
+ k
2
y
. Inserting Eqs. (18.4) and (18.5) into Eq. (18.3), we find
d
2
dz
2
+ fz + κ
2
n
ψ
n
(z)=0 , (18.6)
where
f = eF
2m
r
2
=
eF
E
0
a
2
0
, (18.7)
and E
0
and a
0
are the usual excitonic units, defined in Chap. 10. Eq. (18.7)
shows that fa
3
0
is the ratio between the dipole energy in the field and the
exciton Rydberg energy, ea
0
F/E
0
. Introducing the dimensionless variable
Z by
Z = f
1/3
z (18.8)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 351
and substituting
ζ
n
= Z + κ
2
n
f
−2/3
= Z +(a
0
κ
n
)
2
E
0
a
0
eF
2/3
, (18.9)
we find
ψ
n
(ζ
n
)=−ζ
n
ψ
n
(ζ
n
) , (18.10)
where ψ
n
(ζ)=d
2
ψ
n
/dζ
2
. The solution of Eq. (18.10) is
ψ
n
(z)=a
n
Ai(−ζ
n
) , (18.11)
where Ai(x) is the Airy function (Abramowitz and Stegun, 1972),
Ai(x)=
1
π
∞
0
du cos
u
3
3
+ ux
, (18.12)
and a
n
is a normalization constant. The Airy function decays exponentially
for positive arguments
lim
x→∞
Ai(x)=
1
2
√
πx
1/4
e
−
2
3
x
3/2
1 −
3c
1
2x
3/2
, (18.13)
with c
1
=15/216. For negative arguments, the Airy function oscillates,
lim
x→∞
Ai(−x)=
1
√
πx
1/4
sin
2
3
x
3/2
+
π
4
, (18.14)
expressing the accelerating action of the field. The normalization constant
a
n
is determined by
a
−2
n
=
∞
−∞
dz|Ai(−ζ
n
)|
2
= lim
L→∞
L
−L
dz|Ai(−ζ
n
)|
2
, (18.15)
or, using Eqs. (18.8) and (18.9),
f
1/3
a
2
n
= lim
L→∞
Lf
1/3
−Lf
1/3
dx |Ai(x)|
2
. (18.16)
With partial integration we obtain
Lf
1/3
−Lf
1/3
dx|Ai(x)|
2
= xAi
2
(x)|
Lf
1/3
−Lf
1/3
−
Lf
1/3
−Lf
1/3
dx2xAi(x)Ai
(x) . (18.17)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
352 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Because Ai(x) satisfies the differential equation
Ai
(x)=xAi(x) , (18.18)
we get
Lf
1/3
−Lf
1/3
dx |Ai(x)|
2
= xAi
2
(x)|
Lf
1/3
−Lf
1/3
−
Lf
1/3
−Lf
1/3
dx 2 Ai
(x) Ai
(x)
= xAi
2
(x)|
Lf
1/3
−Lf
1/3
−
Lf
1/3
−Lf
1/3
dx
d
Ai
(x)
2
dx
=
(
xAi
2
(x) −
Ai
(x)
2
)
|
Lf
1/3
−Lf
1/3
. (18.19)
Inserting Eq. (18.19) into Eq. (18.16) yields
a
−2
n
= lim
L→∞
L
f
1/3
1
π
, (18.20)
where we used the fact that Ai(x) and Ai
(x) vanish for x →∞.ForAi(−x)
and Ai
(−x), we inserted the asymptotic expressions given by Eq. (18.14)
and by
lim
x→∞
Ai
(−x)=
x
1/4
√
π
cos
2
3
x
3/2
+
π
4
. (18.21)
The energy eigenvalues are computed from the boundary condition
ψ
n
(z = L)=0 (18.22)
as
2
3
f
L +
κ
2
n
f
3/2
=
n −
1
4
π. (18.23)
Solving Eq. (18.23) for κ
n
and inserting the result into Eq. (18.5) yields
E
n,k
||
=
2
2m
r
,
k
2
||
− Lf +
3πf
2
(n − 1/4)
2/3
-
. (18.24)
Now, we have all the ingredients needed to evaluate Eq. (18.1), which we
write as
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 353
α(ω)=α
b
∞
−∞
dk
x
2π
+∞
−∞
dk
y
2π
n
πf
1/3
√
L
δ(E
n,k
||
+ E
g
− ω)
×
Ai
f
−2/3
k
2
||
−
2m
r
E
n,k
||
2
2
. (18.25)
We change the sum over n to an integral over E
n
→
∞
0
dE
dn
dE
(18.26)
and evaluate the density of states using Eq. (18.23)
dn
dE
=
2m
r
2
π
√
f
L +
κ
2
n
f
1/2
2m
r
2
π
√
f
√
L. (18.27)
We dropped the additive term in L + κ
n
/f, since we are finally interested
in the limit L →∞, see above. Inserting Eq. (18.26) and (18.27) into
Eq. (18.25) yields
α(ω)=α
b
∞
0
dk
2
||
(2π)
2
2m
r
2
f
1/3
Ai
f
−2/3
k
2
||
+
2m
r
(E
g
− ω)
2
7
2
=
α
b
2π
m
r
f
1/3
2
∞
dx |Ai(x)|
2
, (18.28)
where
=
2m
r
(E
g
− ω)
2
f
2/3
=
E
g
− ω
E
0
E
0
ea
0
F
2/3
. (18.29)
Again, we evaluate the integral in Eq. (18.28) by partial integration, fol-
lowing the steps in Eqs. (18.16) – (18.19). The result is
∞
dx |Ai(x)|
2
= −Ai
2
()+[Ai
()]
2
. (18.30)
The total absorption spectrum is thus

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
354 Quantum Theory of the Optical and Electronic Properties of Semiconductors
0
0.5
1
-2 0 2 4 6 8 10
a
-e
Fig. 18.1 Absorption spectrum for free carriers in an electric field according to
Eq. (18.31). The absorption α is given in units of α
= α
b
m
r
f
1/3
/(2π
2
) and is
given by Eq. (18.29)
α(ω)=
α
b
2π
m
r
f
1/3
2
{−Ai
2
()+[Ai
()]
2
} . (18.31)
electroabsorption for free carriers
Fig. 18.1 shows the resulting absorption as function of . The oscillatory
character of the Airy functions for negative arguments leads to oscillations
in the absorption spectrum above the band gap. The amplitude of these
oscillations decreases with increasing energy. We can also see from Fig. 18.1
that the absorption has a tail below the gap, i.e., for ω<E
g
or >0.
Using the asymptotic form (18.13) and
lim
x→∞
Ai
(x)=
x
1/4
2
√
π
e
−
2
3
x
3/2
1+
21c
1
10x
3/2
, (18.32)
we obtain the below-gap absorption as

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 355
α(ω)
α
b
32π
2
f
E
g
− ω
exp
,
−
4
3f
2m
r
(E
g
− ω)
2
3/2
-
. (18.33)
Franz-Keldysh effect
Eq. (18.33) describes the exponential low energy absorption tail which is
caused by the electric field f . The frequency range of this tail increases with
f. One may understand the appearance of the absorption tail as a photon-
assisted field-induced tunneling of an electron from the valence band into
the conduction band.
The absorption spectrum far above the band edge, ω>>E
g
or <<0,
can be estimated using Eqs. (18.14) and (18.21) with the result
α(ω)=
α
b
(2π)
2
2m
r
2
3/2
ω − E
g
. (18.34)
Eq. (18.34) is nothing but the free-carrier absorption result of Chap. 5 for
a 3d-system.
18.2 Quantum Wells
If one applies the electric field perpendicular to the layer of a quantum
well, the situation is quantitatively different from that in bulk material.
Because of the opposite charges, the field pushes electron and hole toward
theoppositewallsofthewell. Hence,theoverlapbetweenthecorresponding
particle-in-a-box wave functions is drastically modified. To discuss this
effect, we again disregard for the time being the modifications caused by
the electron–hole Coulomb interaction.
In a spatially inhomogeneous situation, such as in a quantum well, one
has to use a two-point susceptibility function in real space representation
χ(R, R
,ω), which connects nonlocally the polarization and the field ac-
cording to
P (R,ω)=
d
3
R
χ(R, R
,ω)E(R
,ω) . (18.35)
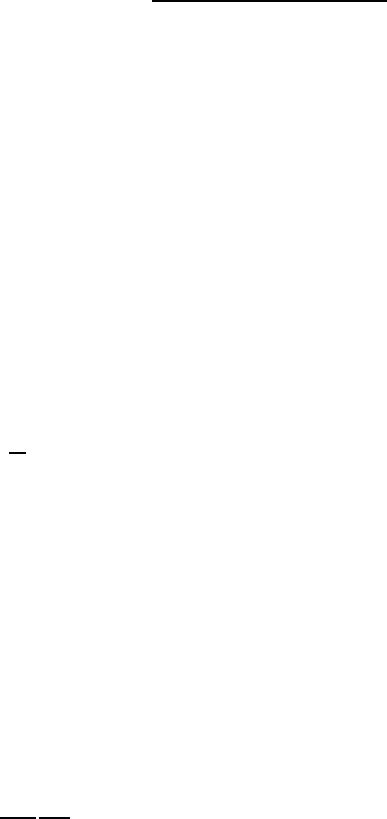
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
356 Quantum Theory of the Optical and Electronic Properties of Semiconductors
The optical susceptibility is given by a generalization of Eq. (18.1) as
χ(R, R
,ω)=χ
0
µ
ψ
∗
µ
(R, r =0)ψ
µ
(R
, r
=0)
(ω + iδ) − E
µ
. (18.36)
Here, ψ
µ
(R, r) is the wave function of an electron–hole pair, and R, r are
the center-of-mass and relative coordinates, respectively. In spatially homo-
geneous situations, χ depends only on R − R
. The Fourier transform with
respect to the difference of the center-of-mass coordinates yields the spatial
dispersion, i.e., the wave-vector dependence of the susceptibility discussed
in Chap. 11. However, due to the spatially inhomogeneous situation in a
quantum well one has
χ(R, R
,ω) = χ(R − R
,ω) .
The light wave length in the visible range is of the order of 10
−4
cm. This
is much larger than the typical quantum-well width, which for GaAs is
around 10
−6
cm. Therefore, it is useful to introduce a susceptibility which
is averaged over the quantum-well volume,
¯χ =
1
V
d
3
R
d
3
R
χ(R, R
,ω) . (18.37)
This averaged susceptibility locally connects the optical polarization and
the electromagnetic field.
Let us consider, for simplicity, a potential well of infinite depth extend-
ing over −L/2 ≤ z ≤ L/2. The pair wave function of a narrow quantum
well can be taken as the product of particle-in-a-box wave functions for the
electron and hole times the function describing the relative motion in the
plane of the layer
ψ
µ
(R, r)=ψ
n
e
(z
e
)ψ
n
h
(z
h
)φ
k
||
(r
||
) . (18.38)
Electron and hole wave functions in the z direction obey the equation
−
2
2m
i
d
2
dz
2
i
± eEz
i
ψ
n
i
(z
i
)=E
n
i
ψ
n
i
(z
i
) , (18.39)
where the +(−) sign is linked to i = e(h). The boundary conditions are
ψ
n
i
(z = ±L/2) = 0 . (18.40)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Electroabsorption 357
Without the field the wave functions are just the simple trigonometric func-
tionswithevenandoddparity
ψ
0
n
(z)=
cos(k
n
z)
sin(k
n
z)
7
with k
n
=
π
L
2n+1
2n
7
for n =0, 1, 2,... . (18.41)
The absorption spectrum resulting from Eqs. (18.36) – (18.41) is
α(ω)=
α
b
L
k
||
,n
e
,n
k
δ(ω − E
g
− E
k
||
− E
n
e
− E
n
h
)
A
n
e
A
n
h
×
+L/2
−L/2
dz ψ
n
e
(z) ψ
n
h
(z)
2
, (18.42)
quantum confined Franz-Keldysh spectrum
with E
k
||
=
2
k
2
||
2m
and the normalization
A
n
i
=
+L/2
−L/2
dz |ψ
n
i
(z)|
2
.
The overlap integral in Eq. (18.42) results from the spatial average,
Eq. (18.37), over R
z
= z
e
= z
h
= z, because r
z
= z
e
− z
h
=0accord-
ing to (18.36), and in the same way over R
z
.
Eq. (18.39) is again solved in terms of Airy functions. However, in order
to fulfill the boundary conditions, we have to use a linear combination of
the two independent types of Airy functions Ai(ζ) and Bi(ζ),where
Bi(x)=
1
π
∞
0
du
e
−
u
3
3
+ux
+sin
u
3
3
+ ux
, (18.43)
see Abramowitz and Stegun (1972). The solution of Eq. (18.39) is thus
ψ
n
i
(z
i
)=a
i
Ai(ζ
i
)+b
i
Bi(ζ
i
) , (18.44)
with
ζ
n
i
= ±f
1/3
z
i
− κ
2
n
i
f
−2/3
. (18.45)
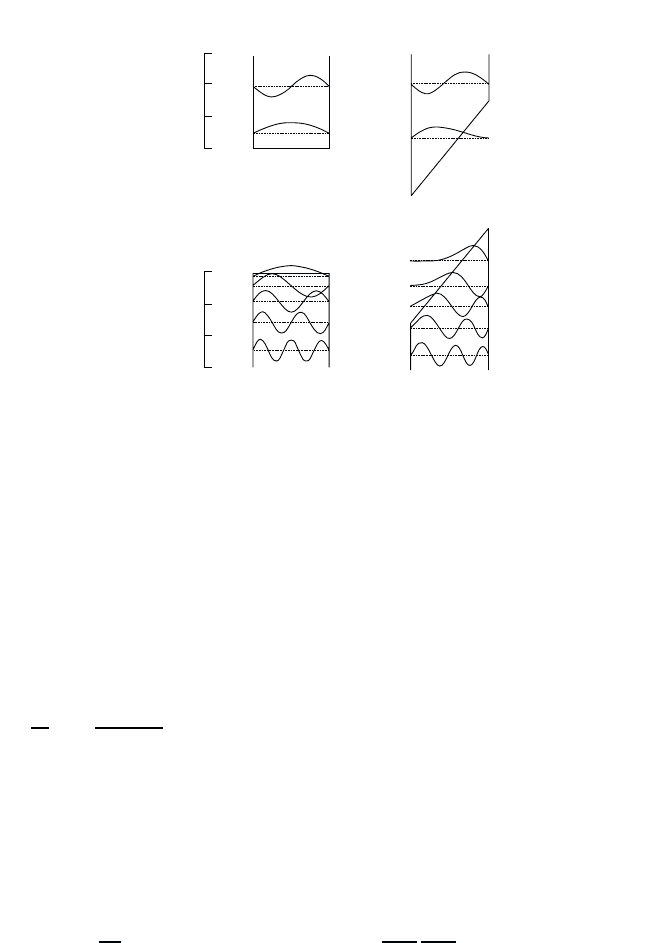
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
358 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Valence Band
Energy (meV)
100
0
Conduction Band
Energy (meV)
0
100
1
2
1
2
1
2
3
4
5
1
2
3
4
5
Fig. 18.2 Calculated wave functions and energy levels for a 150 Å thick GaAs-like
quantum well at 0 and 10
5
Vcm
−1
.[AfterSchmitt-Rinket al. (1989).]
The boundary condition yields the requirement for the existence of solutions
Ai(ζ
i+
)Bi(ζ
i−
)=Ai(ζ
i−
)Bi(ζ
i+
) (18.46)
and
b
i
a
i
= −
Ai(ζ
i+
)
Bi(ζ
i+
)
, (18.47)
where ζ
i±
corresponds to z
i
= ±L/2. Eq. (18.46) determines the energies
κ
2
n
i
and Eq. (18.47) yields the relative weight of the Airy functions Bi and
Ai. The summations over n
e
and n
h
in Eq. (18.42) are now replaced by
integrations over the energies E
e
and E
h
α(ω)=
α
b
L
k
||
∞
−eEL/2
dE
e
∞
−eEL/2
dE
h
dn
e
dE
e
dn
e
dE
e
×δ(ω − E
g
− E
k
||
− E
e
− E
h
) I
eh
, (18.48)
