Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.


January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Chapter 9
Retarded Green’s Function for
Electrons
In the treatment of the classical oscillator model in Chap. 1, we have seen
how a retarded Green’s function determines the response of the oscillator
to a driving field. In this chapter, we will now discuss how a retarded
Green’s function can also be introduced for quantum-mechanical many-
body systems, such as the electron gas of Chap. 7. The retarded Green’s
function contains information about the spectral properties of the system,
i.e., about the changes of the single-particle energies which occur due to the
interactions with other particles of fields. Furthermore, retarded Green’s
functions of many-body systems determine the linear response to external
fields in the same way as for the classical oscillator.
9.1 Definitions
We define the retarded Green’s function for electrons as
G
r
ss
(rt, r
t
)=−
i
θ(t − t
)[ψ
s
(r,t) ,ψ
†
s
(r
,t
)]
+
. (9.1)
The average ... stands for tr (ρ...), the statistical operator ρ being
taken at some fixed initial time, e.g., t = −∞. Due to the step function
θ(t − t
),G
r
is retarded with G
r
(t, t
)=0for t
>t.
Let us express the retarded Green’s function in terms of its two operator
products
G
r
ss
(rt, r
t
)=θ(t − t
)
−
i
ψ
s
(r,t)ψ
†
s
(r
,t
)−
i
ψ
†
s
(r
,t
)ψ
s
(r,t)
≡ θ(t − t
)
G
>
ss
(rt, r
t
) − G
<
ss
(rt, r
t
)
. (9.2)
149
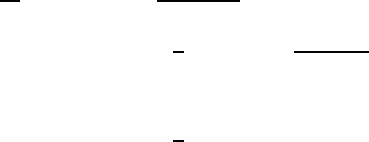
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
150 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Here, we have defined two new Green’s functions G
>
(speak G greater)
and G
<
(speak G lesser). They can be considered as generalizations of the
reduced density matrix for a two-time-dependent correlation function. In
particular G
<
is called the particle propagator. Its equal time limit is up
to the factor i/ identical to the single-particle reduced density matrix. It
describes the kinetics in nonequilibrium systems, where one has to calculate
not only the spectral properties contained in (9.1), but also the evolution of
the particle distribution over these renormalized states, as will be outlined
further in the appendix.
The following manipulations show that, as its classical counterpart, the
quantum mechanical Green’s function G
r
also obeys a differential equation
with an inhomogeneity given by delta functions in space and time. The
equation of motion for the retarded Green’s function is
i
∂
∂t
G
r
ss
(rt, r
t
)=
∂θ(t − t
)
∂t
[ψ
s
(r,t),ψ
†
s
(r
,t
)]
+
−
i
θ(t − t
)
i
∂ψ
s
(r,t)
∂t
,ψ
†
s
(r
,t
)
+
= δ(t−t
)[ψ
s
(r,t),ψ
†
s
(r
,t)]
+
−
i
θ(t−t
)[[ψ
s
(r,t), H(t)],ψ
†
s
(r
,t
)]
+
, (9.3)
where the Heisenberg equation i ∂ψ/∂t =[ψ, H] has been used. The equal
time anti-commutator in the first term of Eq. (9.3) is
[ψ
s
(r,t),ψ
†
s
(r
t)]
+
= δ(r − r
)δ
s,s
, (9.4)
so that a differential equation for the Green’s function results which has a
singular inhomogeneity in space and time:
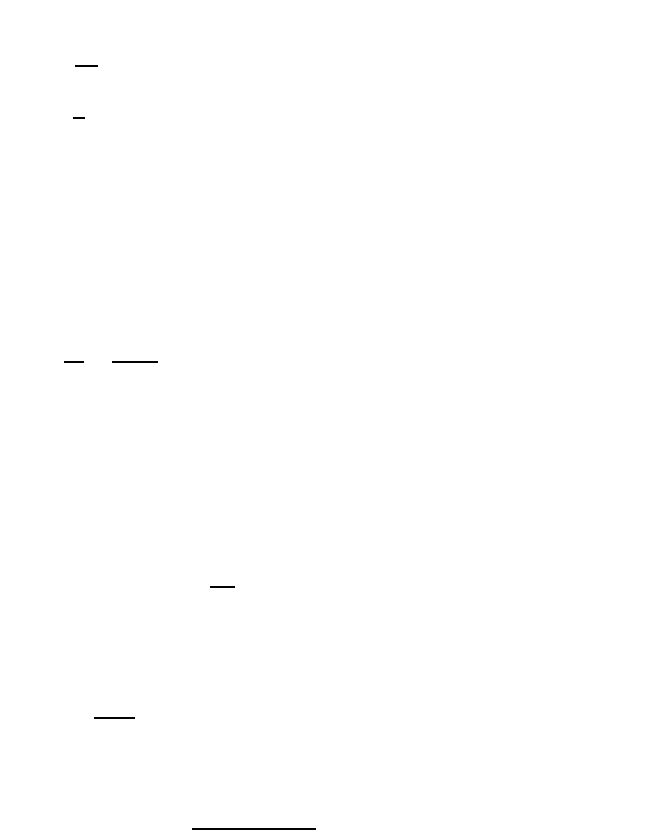
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Retarded Green’s Function for Electrons 151
i
∂
∂t
G
r
ss
(rt, r
t
)=δ(t − t
)δ(r − r
)δ
s,s
−
i
θ(t − t
)
[ψ
s
(r,t), H(t)],ψ
†
s
(r
,t
)
+
. (9.5)
equation of motion for retarded Green’s function
Let us first consider the ideal Fermi gas with the Hamiltonian (6.4). Evalu-
ating the commutator in the second term on the RHS of Eq. (9.5) we obtain
the equation of motion for this simple case as
i
∂
∂t
+
2
∇
2
2m
G
r
0,ss
(rt, r
t
)=δ(t −t
)δ(r − r
)δ
s,s
. (9.6)
Here, we introduced the subscript 0 to indicate that we are dealing with
the noninteracting situation. Eq. (9.6) shows that G
r
0
is diagonal in the
spin indices and depends only on the relative coordinates ρ = r − r
and
τ = t −t
. Taking the Fourier transform of Eq. (9.6) with respect to ρ and
τ and introducing the notation
G
r
0,ss
(ρ,τ)=
k
dω
2π
e
i(k·ρ−ωτ)
G
r
0,ss
(k,ω) , (9.7)
the Green’s function equation for the ideal Fermi gas becomes
ω −
2
k
2
2m
G
r
0,ss
(k,ω)=δ
s,s
, (9.8)
or
G
r
0,ss
(k,ω)=δ
s,s
1
(ω −
k
+ iδ)
, (9.9)
with
k
=
2
k
2
/2m. In Eq. (9.9), we included the infinitesimal imaginary
part +iδ which shifts the poles to the lower half of the complex frequency
plane. As discussed in Chap. 1, this shift guarantees the correct retardation,
i.e., G
r
(τ<0) = 0. It is seen from Eq. (9.9) that the poles of the retarded
Green’s function give the single-particle energies
k
.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
152 Quantum Theory of the Optical and Electronic Properties of Semiconductors
It is worthwhile to look at the time variation of the free particle retarded
Green function by taking the Fourier transform of (9.9)
G
r
0,ss
(k,t− t
)=
dω
2π
G
r
0,ss
(k,ω)e
−iω(t−t
)
=
dω
2π
δ
s,s
e
−iω(t−t
)
(ω −
k
+ iδ)
= −iδ
s,s
θ(t − t
)e
−i
k
(t−t
)
. (9.10)
Here, we used the same complex integration arguments as discussed in the
context of Eq. (1.63). From the resulting expression in Eq. (9.10) we see
that the retarded free-electron Green’s function oscillates in time simply
with the kinetic energy of the electron.
9.2 Interacting Electron Gas
Writing the electron gas Hamiltonian of Chap. 7 in terms of field creation
and destruction operators, we obtain
H =
s
d
3
rψ
†
s
(r)
−
2
∇
2
2m
ψ
s
(r) (9.11)
+
1
2
s,s
d
3
rd
3
r
ψ
†
s
(r)ψ
†
s
(r
)
e
2
0
|r − r
|
ψ
s
(r
)ψ
s
(r)
−
s
d
3
rd
3
r
ψ
†
s
(r)
e
2
n(r
)
0
|r − r
|
ψ
s
(r)+
e
2
2
d
3
rd
3
r
n(r)n(r
)
0
|r − r
|
,
where n(r) is the background charge distribution, which is not treated as
an operator in the jellium approximation. With the Hamiltonian (9.11), we
evaluate the commutator in Eq. (9.5):
[ψ
s
(r,t), H(t)] = −
2
∇
2
2m
ψ
s
(r,t)
+
s
d
3
r
V (r − r
)ψ
†
s
(r
,t)ψ
s
(r
,t)ψ
s
(r,t)
−
d
3
r
V (r − r
) n(r
) ψ
s
(r,t) . (9.12)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Retarded Green’s Function for Electrons 153
Inserting Eq. (9.12) into Eq. (9.5), we see that the Coulomb interaction
gives rise to two additional terms in the equation of motion:
−
i
θ(t− t
)
d
3
r
V (r − r
)
(
s
[ψ
†
s
(r
,t)ψ
s
(r
,t)ψ
s
(r,t) ,ψ
†
s
(r
,t
)]
+
−n(r
)[ψ
s
(r,t),ψ
†
s
(r
,t
)]
+
)
. (9.13)
Hence, as a consequence of the interaction, higher order Green’s functions
with more than two electron operators also appear. The simplest possible
approximation is to factorize the four-operator expectation values in the
first term of Eq. (9.13) into products of two-operator expectation values.
These can be arranged into two terms, each containing a retarded Green’s
function:
−
i
θ(t − t
)[ψ
†
s
(r
,t)ψ
s
(r
,t)ψ
s
(r,t) ,ψ
†
s
(r
,t
)]
+
(9.14)
ψ
†
s
(r
,t)ψ
s
(r
,t)G
r
ss
(rt, r
t
) −ψ
†
s
(r
,t)ψ
s
(r,t)G
r
s
s
(r
t, r
t
) .
The minus sign in the second term arises because we had to commute
two electron annihilation operators before taking the expectation values.
Inserting Eq. (9.14) into Eq. (9.13) yields
d
3
r
V (r − r
)
,
s
ψ
†
s
(r
,t)ψ
s
(r
,t)−n(r
)
G
r
ss
(rt, r
t
)
−
s
ψ
†
s
(r
,t)ψ
s
(r,t)G
r
s
s
(r
t, r
t
)
-
. (9.15)
The first term, also called the Hartree term, contributes only if charge
neutrality is locally disturbed, i.e., if
s
ψ
†
s
(r
,t)ψ
s
(r
,t) = n(r
) . (9.16)
However, the second term, also called Fock or exchange term, always yields
an energy reduction due to the exchange-hole around each Fermion, as
discussed in Chap. 7.
Generally, the Green’s function equation of motion for an interacting
system can be written in the form of a Dyson equation:

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
154 Quantum Theory of the Optical and Electronic Properties of Semiconductors
i
∂
∂t
−
2
∇
2
2m
G
r
ss
(rt, r
t
)=δ(t − t
)δ(r − r
)δ
s,s
+
s
d
3
r
dt
Σ
r
ss
(rt, r
t
)G
r
s
s
(r
t
, r
t
) . (9.17)
Dyson equation for retarded Green’s function
Here, we have introduced Σ
r
as the retarded self-energy which combines all
those terms appearing as a consequence of the many-body interaction. In
order to reproduce the results of our factorization approximation, we have
to choose the Hartree–Fock self-energy as
Σ
r
ss
(rt, r
t
)=δ(t −t
)
(
δ(r − r
)δ
s,s
×
d
3
r
1
V (r − r
1
)
s
1
ψ
†
s
1
(r
1
,t)ψ
s
1
(r
1
,t)−n(r
1
)
− V (r − r
)ψ
†
s
(r
,t)ψ
s
(r,t)
)
, (9.18)
where the second term is the exchange self-energy. The Hartree–Fock self-
energy approximation is instantaneous, i.e., not retarded.
For homogeneous stationary systems, G
r
and Σ
r
depend only on the
relative coordinates r − r
= ρ and t − t
= τ, and not on the center-of-
mass coordinates (r + r
)/2 and (t + t
)/2. Furthermore, we assume for
simplicity that the Green’s function and the self-energy are both diagonal
in the spin index. Taking the Fourier transform with respect to ρ and τ,
as defined in Eq. (9.7), the Dyson equation (9.17) takes the form
ω −
2
k
2
2m
G
r
ss
(k,ω)=1+Σ
r
ss
(k,ω)G
r
ss
(k,ω) (9.19)
or
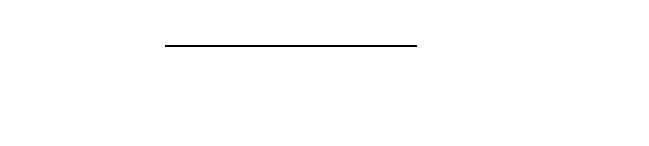
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Retarded Green’s Function for Electrons 155
G
r
ss
(k,ω)=
1
[ω + iδ −
k
− Σ
r
ss
(k,ω)]
. (9.20)
retarded electron Green’s function
Equation (9.20) shows that the free-particle energy
k
is replaced by
k
+
Σ
r
(k,ω) as a consequence of the interactions, thus explaining the origin
of the name self-energy. Usually, the self-energy is a complex frequency-
dependent function. In the static limit (ω =0), the real part of Σ
r
yields
a shift of the single-particle energies due to the many-body interactions,
and the imaginary part describes the corresponding broadening (inverse
damping time).
As illustrative example, we now evaluate the self-energy, Eq. (9.18), for
spatially and temporally homogeneous systems. As mentioned earlier, the
Hartree term vanishes in this case as a consequence of charge neutrality.
For the exchange term, we get
Σ
r
exc,ss
(k,ω)=−
q
V
|k−q|
n
q
, (9.21)
where ψ(r,t)=
k
e
ik·r
a
k
(t) (with L
3
≡ 1 for simplicity) and
ψ
†
(r
,t)ψ(r,t) =
k,k
a
†
k
(t)a
k
(t)e
i(k·r−k
·r
)
=
k
n
k
e
ik·(r−r
)
(9.22)
have been used. For a thermal electron distribution, n
k
is given by the
Fermi distribution f
k
, and the exchange self-energy is
Σ
r
exc,ss
(k,ω)=−
q
V
|k−q|
f
q
. (9.23)
Hence, as a consequence of the exchange interaction, all single-particle en-
ergies
k
are replaced by the renormalized energies
e
k
=
k
+ Σ
r
exc
(k) . (9.24)
In order to estimate the numerical value of the energy shift for the case
of a degenerate electron plasma, we approximate the relevant momentum

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
156 Quantum Theory of the Optical and Electronic Properties of Semiconductors
transfer by the Fermi wave number
|k − q|k
F
. (9.25)
Then Eq. (9.23) yields
Σ
r
exc,ss
−
q
V
k
F
f
q
= −
1
2
V
k
F
n, (9.26)
where the factor 1/2 appears since we do not sum over the spin. Us-
ing the expression for the Fermi wave number, Eq. (6.22), and the three-
dimensional Coulomb potential, Eq. (7.33), we see that the exchange energy
varies with the plasma density as
Σ
r
exc,ss
−
2
3
2/3
π
1/3
e
2
0
n
1/3
. (9.27)
Eq. (9.27) shows that the energy reduction per particle increases with in-
creasing plasma density n. This increase is proportional to n
1/3
, i.e., pro-
portional to the inverse mean inter-particle distance. Basically the same
result has already been obtained in Eq. (7.47), where we analyzed the to-
tal exchange energy of the system. All these results are a consequence of
the net energy gain (reduced Coulomb repulsion) resulting from the Pauli
exclusion principle causing particles with equal spin to avoid each other.
Qualitatively, we can estimate this energy gain as the Coulomb energy
e
2
/
0
r evaluated for r = n
−1/3
.
For a quasi-two dimensional system, we have to evaluate Eq. (9.26)
with V
q
and k
F
given by Eqs. (7.59) and (7.69), respectively. The resulting
exchange self-energy varies as −n
1/2
. In two dimensions, the energy gain
due to the exchange hole is (e
2
/
0
)n
−1/2
,wheren
−1/2
measures the distance
between particles.
9.3 Screened Hartree–Fock Approximation
Semiconductors under optical excitation or with an injected current are
ideally suited to study the density-dependent renormalizations of the single-
particle energies, because one can vary the plasma density in these systems
over many orders of magnitude. To obtain a realistic estimate for the
single-particle energy renormalization, we now make use of the plasmon–
pole approximation. Basically, we extend the Hartree–Fock approximation
of the previous section by replacing the bare Coulomb potential V
q
with the

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Retarded Green’s Function for Electrons 157
screened one, V
s
(q, ω)=V
q
/(q, ω). However,wewillseethatwehaveto
include a correlation self-energy at the same time, the so-called Coulomb-
hole self-energy, which describes the energy reduction due to the depletion
shell around a given charged particle.
As a consequence of the frequency dependence of V
s
(q, ω), the resulting
retarded self-energy is also frequency-dependent and cannot simply be in-
terpreted as single-particle energy shift. In order to avoid this complication,
we restrict our treatment to the static approximation
V
s
(q)=
V
q
(q, 0)
. (9.28)
Replacing V
q
by V
s
(q) in the exchange self-energy, Eq. (9.23), we obtain
Σ
r
exc,ss
(k)=−
k
V
s
(|k − k
|)f
k
≡ Σ
r
SX
(k) . (9.29)
screened exchange self-energy
In Sec. 9.2, we discuss that the momentum transfer in a degenerate plasma
is of the order of k
F
, allowing us to approximate Eq. (9.29) as
Σ
r
SX
(k 0) −
1
2
nV
s
(k
F
) . (9.30)
This expression can be evaluated using the plasmon–pole approximation.
We obtain for the three-dimensional system
Σ
r
SX
−
1
2
n
4πe
2
0
k
2
F
1 −
ω
2
pl
ω
2
k
F
, (9.31)
where ω
2
q
and ω
2
pl
are given by Eqs. (8.86) and (8.31), respectively. In the
two dimensional case, we get
Σ
r
SX
−
1
2
n
2πe
2
0
k
F
1 −
ω
2
pl
(k
F
)
ω
2
k
F
, (9.32)
where Eqs. (8.88) and (8.69)have been used.
A comparison of these results with the experiment and with a detailed
derivation shows that the screened exchange self-energy underestimates the
true single-particle energy shifts. This is not astonishing since, as we have
mentioned before, there has to be an additional contribution due to the
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
158 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Coulomb correlation effects not included in the Hartree–Fock theory. The
corresponding term which appears in addition to the screened exchange
self-energy, is called the Coulomb hole self-energy,
CH
. The origin of
this name is due to the strong reduction of the pair correlation function
R
ss
(|r − r
| =0)also for electrons with different spin, s = s
, when the
proper Coulomb correlations are included in the many-electron wave func-
tion. In analogy to the “exchange hole” discussed in Chap. 7, this correlation
effect is referred to as “Coulomb hole”. Hence, the Coulomb-hole self-energy
describes the reduction of the total energy due to the fact that the elec-
trons avoid each other because of their mutual Coulomb repulsion. The
renormalized single-particle energy is instead of Eq. (9.24)
e
k
=
k
+Σ
SX
(k)+Σ
CH
. (9.24a)
The derivation of the Coulomb-hole contribution to the self-energy is
presented in later chapters of this book. There, we also discuss the corre-
sponding change of the effective semiconductor band gap. Here, we only
want to mention that this contribution can be calculated as the change of
the self-interaction of a particle with and without the presence of a plasma,
i.e.,
Σ
CH
=
1
2
lim
r→0
[V
s
(r) − V (r)] . (9.33)
Ignoring for the moment the term ∝ q
4
in the effective plasmon frequency ω
q
of the single-plasmon-pole approximation, one obtains for V
s
(r) the Yukawa
potential, Eq. (8.61), both in 2d and 3d. Using the Yukawa potential in
Eq. (9.33) we obtain the Coulomb-hole self-energy as
Σ
CH
= −
e
2
2
0
κ, (9.34)
where we have included static screening through
0
and κ is the screening
wave number in 2d or 3d, respectively.
For the three-dimensional system, it is possible to improve the result
(9.34) by analytically evaluating V
s
(r) using the full static plasmon–pole
approximation,
V
s
(r)=
L
3
(2π)
3
d
3
qV
s
(q)e
−iq·r
, (9.35)
