Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Plasmons and Plasma Screening 139

yields

eff

(q)=V

[1 + V

eff

(q)P

(q, ω)] (8.50)

eff

(q)=

1 − V

(q, ω)

(q, ω)

≡ V

(q, ω) . (8.51)

Here, we introduced V

(q, ω) as the dynamically screened Coulomb potential.

The dynamic dielectric function (q,ω) is given by

(q, ω)=1− V

(q, ω) , (8.52)

or, using Eq. (8.23)

(q, ω)=1− V



k−q

− f

(ω + iδ + 

k−q

− 

)

. (8.53)

Lindhard formula for the longitudinal dielectric function

The Lindhard formula describes a complex retarded dielectric function,

i.e., the poles are in the lower complex frequency plane, and it includes

spatial dispersion (q dependence) and temporal dispersion (ω dependence).

Eq. (8.53) is valid both in 3 and 2 dimensions. In the derivation, we some-

times used the 3D expressions, but that could have been avoided without

changing the ﬁnal result. Note, that the expectation value f

of the par-

ticle density operator is equal to the Fermi–Dirac distribution function f

for a thermal plasma. However, Eq. (8.53) is valid also for nonequilibrium

distribution functions.

The longitudinal plasma eigenmodes are obtained from

Re[(q, ω)] = 0 or 1=V

Re[P

(q, ω)] . (8.54)

longitudinal eigenmodes

This equation is identical to the plasma eigenmode equation (8.25). Hence,

our discussion of plasma screening of the Coulomb potential and of the col-

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

140 Quantum Theory of the Optical and Electronic Properties of Semiconductors

lective plasma oscillations obtained from (q, ω)=0, shows that screening

and plasmons are intimately related phenomena.

8.3 Analysis of the Lindhard Formula

To appreciate the Lindhard (or RPA) result, we discuss some important

limiting cases in 3D and 2D systems.

8.3.1 Three Dimensions

In the long wave-length limit, q → 0, we repeat the steps described by

Eqs. (8.26) – (8.31) to obtain

(0,ω)=1−

, (8.55)

the classical (or Drude) dielectric function, which is the same as the result

obtained for the oscillator model in Chap. 1.

In the static limit, ω + iδ → 0, Eq. (8.53) yields

(q, 0) = 1 − V



k−q

− f

k−q

− E

. (8.56)

Using the expansions (8.26) and (8.27) again and assuming a thermal equi-

librium Fermi–Dirac carrier distribution, we can write



∂f

∂k

= −



∂f

∂µ

∂

∂k

= −





∂f

∂µ

. (8.57)

This way we ﬁnd

(q, 0) = 1 +

4πe



∂

∂µ



=1+

4πe



∂n

∂µ

≡ 1+

. (8.58)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Plasmons and Plasma Screening 141

Here, we introduced

κ =



4πe



∂n

∂µ

(8.59)

3D screening wave number

as the inverse screening length, i.e., the screening wave number.Using

(8.58) in (8.51) we ﬁnd the statically screened potential

(q)=

4πe



+ κ

(q, 0)

. (8.60)

3D statically screened Coulomb potential

This result shows nicely how the plasma screening removes the divergence

at q → 0 from the Coulomb potential. Taking the Fourier transformation

of Eq. (8.60) yields

(r)=



4πe



+ κ

)

iq·r



−κr

, (8.61)

compare Eqs. (7.31) – (7.32) without the limit γ → 0. The statically

screened Coulomb potential is plotted in Fig. 8.3 together with the bare

potential. The comparison shows that the long-ranged bare Coulomb po-

tential is screened to a distance 1/κ. The statically Coulomb potential,

Eq. (8.61) is often called Yukawa potential.

The inverse screening length given by Eq. (8.59) can be evaluated ana-

lytically for the two limiting cases of i) a degenerate electron gas where the

Fermi function is the unit-step function and ii) for the nondegenerate case

where the distribution function is approximated as Boltzmann distribution.

In the literature, the theory of screening in the degenerate (T =0)electron

gas is often referred to as Thomas–Fermi screening. In Chap. 6, where we

discussed some properties of the degenerate electron gas, we found that the

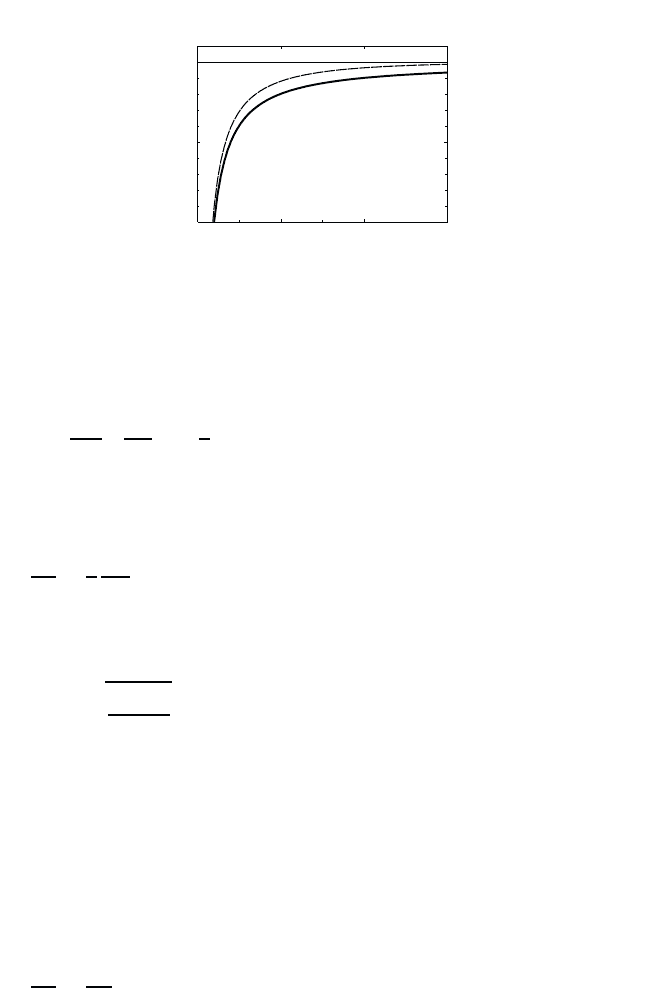
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

142 Quantum Theory of the Optical and Electronic Properties of Semiconductors

-10

-5

0.5 1 1.5

V/e

V (r)

V(r)

Fig. 8.3 Statically screened (thin line) and unscreened (thick line) Coulomb potential

for a three-dimensional system.

density can be written as

n =

2π





3/2

, (8.62)

where the Fermi energy E

≡ µ(T =0). From Eq. (8.62) we obtain

∂n

∂µ

, (8.63)

so that the screening wave number (8.59) in this case becomes

κ =



6πe



. (8.64)

3D Thomas–Fermi screening wave number

The theory of screening in the nondegenerate limit is known as Debye–

Hückel screening. For this case, we approximate the Fermi distribution by

the Boltzmann distribution and use Eq. (6.27) to obtain the derivative of

the chemical potential as

∂µ

∂n

βn

. (8.65)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Plasmons and Plasma Screening 143

InsertingthisintoEq.(8.59)yields

κ =



4πe

nβ



. (8.66)

3D Debye–Hückel screening wave number

8.3.2 Two Dimensions

To investigate the long wave-length limit of the Lindhard formula for a

two-dimensional system, we again insert the expansions (8.26) – (8.28) into

Eq. (8.53) to obtain

(q → 0,ω) − 1=V

mω



(2π)



i,j

∂f

∂k

, (8.67)

where the factor 2 comes from the spin summation implicitly included in



. Partial integration on the RHS of Eq. (8.67) yields with



(2π)

∂f

∂k

= −2



(2π)

∂k

= −nδ

the Drude result

(q → 0,ω)=1−

(q)

, (8.68)

where n is the 2D particle density N/L

. In Eq. (8.68), we introduced the

2D plasma frequency

(q)=



2πe



q . (8.69)

2D plasma frequency

To study the static limit, ω =0, of the Lindhard formula, we use the 2D

Coulomb potential, Eq. (7.59), and obtain

(q, 0) = 1 + V

∂n

∂µ

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

144 Quantum Theory of the Optical and Electronic Properties of Semiconductors

so that

(q, 0) = 1 +

, (8.70)

2D static dielectric function

where the inverse screening length in quasi-two dimensions is

κ =

2πe



∂n

∂µ

. (8.71)

Hence, the statically screened 2D Coulomb potential is

(q)=

2πe



q + κ

. (8.72)

For the chemical potential of the two-dimensional Fermi gas, we have the

explicit result given in Eq. (6.41):

βµ(n, T )=ln



βπn/m

− 1

. (8.73)

Hence, we obtain

∂µ

∂n



1 − e

−

βπn/m

(8.74)

and thus

κ =

2me





(1 − e

−

βπn/m

) . (8.75)

Using the explicit expression for the 2D chemical potential, it is easy to

verify that

1 − e

−

βπn/m

= f

k=0

, (8.76)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Plasmons and Plasma Screening 145

where f

is the Fermi–Dirac distribution of the carriers. Combining (8.75)

and (8.76), the 2D screening wave number assumes the simple form

κ =

2me





k=0

. (8.77)

2D screening wave number

This expression is correct for all densities and temperatures. It is interesting

to note that the screening wave number in 2D becomes independent of the

density for low temperature and high densities, whereas the corresponding

3D result always remains density-dependent.

8.3.3 One Dimension

One could continue along the lines of the three- and two-dimensional anal-

ysis and discuss the RPA screening also for quantum wires. However, we

prefer not to describe these developments, but rather point out a general

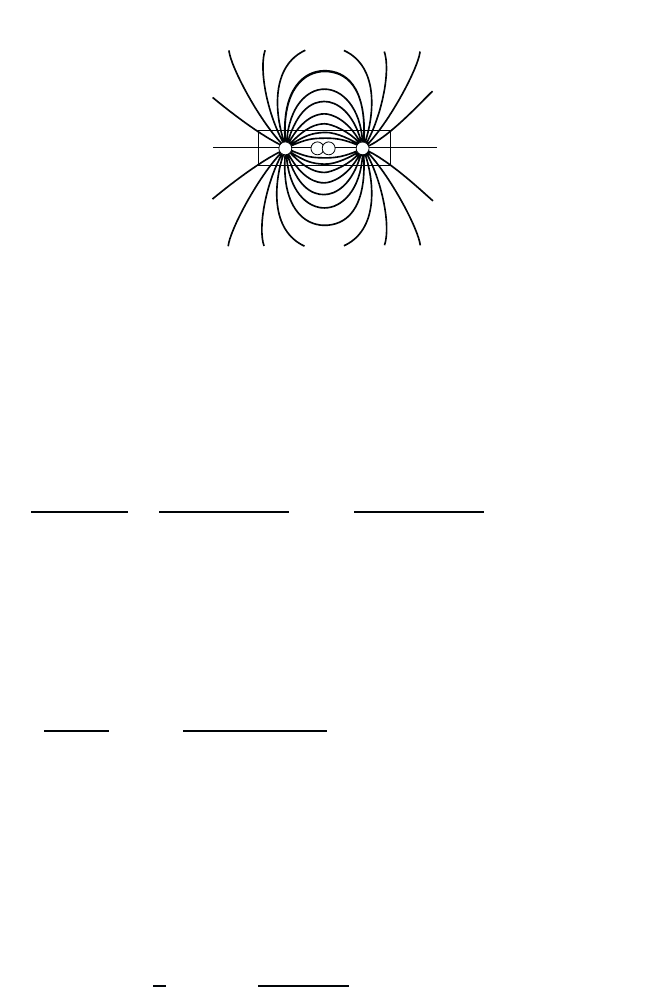
trend of the dimensionality dependence of screening. Let us consider for

example two electrons. In a bulk material, all ﬁeld lines between these

two charges can be screened by other optically excited charged particles.

In quantum wells, already some of the ﬁeld lines pass through the barrier

material. Since the optically excited electrons of holes are conﬁned to the

quantum well, the lines in the barrier material cannot be screened. Si-

multaneously, the density of states is reduced in 2D as compared to 3D.

Correspondingly, the inﬂuence of screening in 2D is considerably weaker

than in 3D, whereas the eﬀects of state ﬁlling become more pronounced.

This trend continues if one passes from 2D quantum wells to quasi-one-

dimensional quantum wires as illustrated in Fig. 8.4.

Obviously, only the ﬁeld lines very close to the wire axis can be screened.

Considering at the same time the further reduced density of states, one can

conclude that screening eﬀects may often be neglected in comparison with

the dominating state ﬁlling eﬀects. In Chap. 13, we present an example

where we compute the nonlinear optical properties of quantum wires, clearly

showing that the results are inﬂuenced only weakly by screening.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

146 Quantum Theory of the Optical and Electronic Properties of Semiconductors

Fig. 8.4 Schematic drawing of the ﬁeld lines in a quantum wire.

8.4 Plasmon–Pole Approximation

Equations (8.55) and (8.68) show that in the long wave-length limit, both

in 3D and 2D, the inverse dielectric function

(q → 0,ω)

(ω + iδ)

− ω

=1+

(ω + iδ)

− ω

(8.78)

has just one pole. We use this observation to construct an approximation

for the full dielectric function (q, ω), which tries to replace the continuum

of poles contained in the Lindhard formula by one eﬀective plasmon pole

at ω

(q, ω)

=1+

(ω + iδ)

− ω

. (8.79)

plasmon–pole approximation

The eﬀective plasmon frequency ω

is chosen to fulﬁll certain sum rules

(Mahan, 1981) which can be derived from the Kramers–Kronig relation,

Eq. (1.23),





(q, ω) − 1=



∞

dω







(q, ω



)

2

− ω

. (8.80)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Plasmons and Plasma Screening 147

We make use of the static long wave-length limit, which for 3D is given by

Eq. (8.58),





(q, 0) − 1=

lim

q→0



∞

dω







(q, ω



)



. (8.81)

This is the so-called conductivity sum rule. According to Eq. (8.79), we

have

(q, ω)=

− ω

(ω + iδ − Ω

)(ω + iδ +Ω

)

(8.82)

where

Ω

= ω

− ω

. (8.83)

Using the Dirac identity in Eq. (8.82) and inserting the result into the RHS

of Eq. (8.81), we ﬁnd

Ω

, (8.84)

where lim

q→0

is implied. Eq. (8.84) yields

lim

q→0

= ω





. (8.85)

Following Lundquist (1967), we therefore choose the form

= ω





+ ν

. (8.86)

3D eﬀective plasmon frequency

The last term ν

in this equation is added in order to simulate the contri-

bution of the pair continuum. Usually we take

= Cq

, (8.87)

where C is a numerical constant. Practical applications show that it is often

suﬃcient to use the much simpler plasmon–pole approximation instead of

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

148 Quantum Theory of the Optical and Electronic Properties of Semiconductors

the full RPA dielectric function to obtain reasonable qualitative results for

the eﬀects of screening.

Similarly, one gets for two-dimensional systems (see problem 8.2)

= ω

(q)

+ ν

(8.88)

as the eﬀective 2D plasmon frequency.

REFERENCES

G.D. Mahan, Many Particle Physics, Plenum Press, New York (1981)

B.I. Lundquist, Phys. Konden. Mat. 6, 193 and 206 (1967)

D. Pines and P. Nozieres, The Theory of Quantum Liquids,Benjamin,

Reading, Mass. (1966)

For the modiﬁcations of the plasmon–pole approximation in an electron–

hole plasma see, e.g.:

R. Zimmermann, Many-Particle Theory of Highly Excited Semiconductors,

Teubner, Berlin (1988)

H. Haug and S. Schmitt–Rink, Prog. Quantum Electron. 9, 3 (1984)

PROBLEMS

Problem 8.1: Use the quasi-2D Coulomb potential

2πe



and apply the classical theory outlined in Chap. 1 to verify that the 2D

plasma frequency is given by Eq. (8.69).

Problem 8.2: Derive the eﬀective plasmon frequency, Eq. (8.88), of the

2D plasmon–pole approximation.