Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.


January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Interacting Electron Gas 119
7.3 Two-Dimensional Electron Gas
Even in those semiconductor structures which we consider as low-
dimensional, such as quantum wells, quantum wires, or quantum dots, the
Coulomb potential varies as 1/r. The reason is that the electric field lines
between two charges are not confined within these structures. The field
lines also pass through the surrounding material, which is often another
semiconductor material with a very similar dielectric constant.
In this section, we discuss the situation of idealized semiconductor quan-
tum wells, where the electron motion is confined to two dimensions, but
the Coulomb interaction has its three-dimensional space dependence. For
simplicity, we disregard here all modifications which occur for different di-
electric constants in the confinement layer and the embedding material. As
introduced in Chap. 4, we assume that the carriers are confined to the x, y
layer and put the transverse coordinate z =0. For this case, we need only
the two dimensional Fourier transform of the Coulomb potential:
V
q
=
d
2
r
L
2
V (r)e
iq·r
(7.57)
with V (r) given by Eq. (7.30). Eq. (7.57) yields
V
q
=
e
2
0
L
2
∞
0
dr
2π
0
dφ e
iqrcosφ
=
2πe
2
0
L
2
q
∞
0
d(qr)J
0
(qr) , (7.58)
where J
0
(x) is the zero-order Bessel function of the first kind. Since
∞
0
dx J
0
(x)=1
we obtain
V
q
= V
2D
q
=
2πe
2
0
L
2
1
q
. (7.59)
quasi-2D Coulomb potential
Eq. (7.59) shows that the Coulomb potential in two dimensions exhibits a
1/q dependence instead of the 1/q
2
dependence in 3D.
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
120 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Using Eq. (7.59) in Eq. (7.46), we obtain the exchange energy as (see
problem 7.1)
E
2D
exc
= −
L
2
e
2
C
3π
0
(2πn)
3/2
, (7.60)
where
C =
l=0,2,...,∞
2
l +2
1
2
l
l
l/2
2
. (7.61)
is a numerical constant and n = N/L
2
.
In order to compare the exchange energy in 2D and 3D, we introduce
the normalized distance r
s
between particles through the relation
4π
3
r
3
s
=
1
na
3
0
=
L
3
Na
3
0
(7.62)
in 3D. Here, a
0
is the characteristic length scale given by the Bohr radius
of the bound electron–hole pairs, i.e., excitons (see Chap. 10 for details).
At this point we use the definition of a
0
as
a
0
=
2
0
me
2
(7.63)
in three dimensions. In two dimensions, we have
πr
2
s
=
1
na
2
0
=
L
2
Na
2
0
, (7.64)
where a
0
now is the 2D Bohr radius, which is half of the 3D Bohr radius.
The 3D exchange energy is seen to vary with the particle distance r
s
as
E
3D
exc
∝−r
−4
s
, (7.65)
whereas
E
2D
exc
∝−r
−3
s
, (7.66)
i.e., in three dimensions the exchange energy falls off more rapidly for larger
distances than in two dimensions. This is a consequence of the larger phase
space volume for D =3compared to the D =2case.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Interacting Electron Gas 121
In the evaluation of the pair correlation function R
ss
(r, r
) for the 2D
electron gas, we obtain formally the same result as in Eq. (7.52), except
now
F (r − r
)=n
J
1
(k
F
|r − r
|)
k
F
|r − r
|
(7.67)
with J
1
being the first-order Bessel function of the first kind. Here we
have introduced the two-dimensional Fermi wave number k
F
through the
relation
N =2
k
f
k
=
L
2
π
k
F
0
dk k . (7.68)
Evaluating Eq. (7.68) yields
k
F
=
√
2πn . (7.69)
The resulting pair correlation function for 2D is plotted in Fig. 7.3.
Schematically, the variations of the correlation function in two-dimensions
resemble those of the three-dimensional result shown in Fig. 7.2. A more
detailed comparison between Figs. 7.2 and 7.3, however, shows that the
oscillatory structures are somewhat more pronounced in the 2D system,
indicating that the exchange correlations of the electrons are stronger in
two than in three dimensions.
0
0.5
1
0
2 4 6 8
s=s'
s=s'
R 4/n
2
k
F
r
Fig. 7.3 Pair correlation function R
ss
for the quasi-two-dimensional electron plasma,
Eqs. (7.52) and (7.67), as function of the dimensionless particle distance k
F
ρ,where
ρ = |r − r
| and k
F
is given by Eq. (7.69).

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
122 Quantum Theory of the Optical and Electronic Properties of Semiconductors
7.4 Multi-Subband Quantum Wells
In order to calculate the properties of electron gases in quantum wells with
several subbands, we have to evaluate the matrix elements of the Coulomb
potential between the various envelope eigenfunctions of the quantum well.
It is convenient to start with the 3D Fourier transform of the Coulomb
potential V
3D
q
of Eq. (7.33), where L
3
has to be replaced by L
2
L
z
with L
z
being the thickness of the quantum well. With this modification, we obtain
the Coulomb potential V
q
(z),wherez is the coordinate perpendicular to
the layer, by a 1D Fourier transform of Eq. (7.33) with respect to the
perpendicular momentum component q
⊥
:
V
q
(z)=
q
⊥
V
3D
q
e
iq
⊥
z
=
4πe
2
0
L
2
L
z
+∞
−∞
dq
⊥
∆q
⊥
e
iq
⊥
z
q
2
+ q
2
⊥
, (7.70)
where we have split the momentum vector into its components parallel and
perpendicular to the plane. With ∆q
⊥
=2π/L
z
we get
V
q
(z)=
2e
2
0
L
2
+∞
−∞
dq
⊥
e
iq
⊥
z
q
2
+ q
2
⊥
=
2πe
2
0
L
2
q
e
−q
|z|
= V
2D
q
e
−q
|z|
. (7.71)
The Coulomb potential of a quasi-2D structure, Eq. (7.59), follows from
this general result in the limit q
|z| 1 .
The matrix elements of the Coulomb interaction V
q
(z
1
− z
2
) between
two electrons at the perpendicular positions z
1
and z
2
described by the

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Interacting Electron Gas 123
envelope functions ζ
n
(z
i
) are
V
n
,m
;m,n
(q
)=
V
2D
q
dz
1
dz
2
ζ
n
(z
2
)ζ
m
(z
1
)e
q
|z
2
−z
1
|
ζ
m
(z
1
)ζ
n
(z
2
) . (7.72)
Coulomb potential for multi-band quantum wells
The interaction Hamiltonian in the multi-subband situation is
ˆ
H
C
=
1
2
n
,m
;n,m
k,k
,q,s,s
V
n
,m
;m,n
(q)ˆa
†
n
,k
−q,s
ˆa
†
m
,k+q,s
ˆa
m,k,s
ˆa
n,k
,s
. (7.73)
Here, the vectors k, k
, q are all momentum wave vectors in the plane of
the quantum well. The resulting exchange energy is
E
exc
= −
1
2
m,n,k,q,s
V
m,n;m,n
(q)f
m,k−q
f
n,k
, (7.74)
where f
m,k
is the occupation probability of state m, k and the term q =0
has to be excluded.
7.5 Quasi-One-Dimensional Electron Gas
Motivated by the success of semiconductor quantum-well structures in per-
mitting the study of quasi-two-dimensional phenomena, there is strong in-
terest in structures with even more pronounced quantum confinement ef-
fects. Examples are the quantum wires where electrons and holes are free to
move in one space dimension, and the quantum dots where the carriers are
confined in all three space dimensions. Quantum dots will be discussed sep-
arately later in this book. In this section, we analyze some of the basic phys-
ical properties of electrons in quantum wires. Quantum wires have been
made in different sophisticated ways, always adding quantum confinement
to restrict the free carrier motion to one dimension. The additional confine-
ment potentials have been generated through various techniques, such as
growth of structures on specially prepared substrates, using grooves, etch-
ing of quantum wells, ion implantation, or with the help of induced stresses

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
124 Quantum Theory of the Optical and Electronic Properties of Semiconductors
in the material below a quantum well.
The analysis of the confinement effects in quantum wires has to be
done carefully. If we simply put the transverse coordinates x = y =0,
we would find that the resulting one-dimensional Coulomb potential has
several pathological features. Loudon showed already in the year 1959 that
the ground-state energy of an electron–hole pair is infinite in one dimension.
In order to obtain a regularized Coulomb potential, we consider a quasi-
one-dimensional quantum wire with a finite but small extension in the
quantum-confined directions. We use the envelope function approximation
for the carrier wave functions and average the Coulomb potential with the
transverse quantized envelope functions. This way, we obtain a mathemati-
cally well-defined, nonsingular interaction potential. The simplest example
is a cylindrical quantum wire of radius R with infinite lateral boundaries.
For this case, the envelope wave function corresponding to the lowest con-
finement energy level is
φ(ρ)=
J
0
(α
0
ρ/R)
√
πRJ
1
(α
0
)
, (7.75)
where J
n
(ρ) is the radial Bessel function of order n. The corresponding
confinement energy is
E
e
=
α
2
0
2
2m
e
R
2
, (7.76)
and α
0
=2.405 is the first zero of J
0
(x)=0. The denominator in Eq. (7.75)
results from the normalization of the wave function (see problem 7.3).
The quasi-one-dimensional (q1D) Coulomb potential between two elec-
trons is obtained by averaging the three-dimensional Coulomb potential
with the radial envelope functions :
V
q1D
(z
1
,z
2
)=
e
2
0
π
2
R
4
J
4
1
(α
0
)
R
0
dρ
1
ρ
1
R
0
dρ
2
ρ
2
2π
0
dθ
1
2π
0
dθ
2
×
J
2
0
(α
0
ρ
1
/R)J
2
0
(α
0
ρ
2
/R)
√
(z
1
−z
2
)
2
+( ρ
1
cos θ
1
−ρ
2
cos θ
2
)
2
+( ρ
1
sin θ
1
−ρ
2
sin θ
2
)
2
.
(7.77)
quasi-1D Coulomb potential
This quasi-one-dimensional Coulomb potential is finite at z ≡ z
1
− z
2
=0
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Interacting Electron Gas 125
and can be approximated quite well by the simple regularized potential
V
q1D
(z)=
e
2
0
1
|z| + γR
, (7.78)
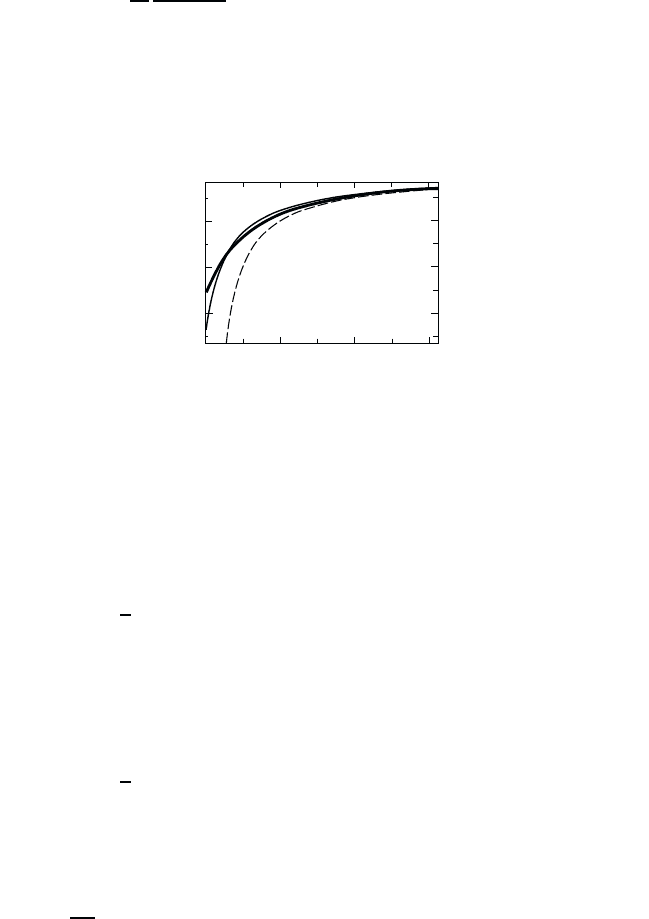
where γ is a fitting parameter which has the value γ 0.3.Asshownin
Fig. 7.4, the potential (7.78) is finite at z =0,andvariesas1/z for large
distances.
-1
-2
-3
0
1
2
3
z
V (z)
1qd
Fig. 7.4 The quasi-one-dimensional Coulomb potential according to Eq. (7.77) as func-
tion of particle separation z (thick solid line). The dashed curve is a Coulomb potential,
and the thin solid line is the regularized Coulomb potential, Eq. (7.78), for γ =0.3.
From Eq. (7.46) we see that the quasi-one-dimensional exchange energy
for a thermal electron gas is
E
q1D
exc
= −
1
2
k,k
,s
V
q1D
|k−k
|
f
k
f
k
, (7.79)
where V
q1D
k
is the Fourier transform with respect to z of (7.77) or its
approximation (7.78). At T =0, Eq. (7.79) yields
E
q1D
exc
= −
1
2
k,k
,s
V
q1D
|k−k
|
θ(E
F
− E
k
) θ(E
F
− E
k
) , (7.80)
and the one-dimensional density is
n =
k
F
π
. (7.81)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
126 Quantum Theory of the Optical and Electronic Properties of Semiconductors
REFERENCES
C. Kittel, Quantum Theory of Solids, Wiley and Sons, New York (1967)
R. Loudon, Am. J. Phys. 27, 649 (1959)
D. Pines, Elementary Excitations in Solids, Benjamin, New York, (1966)
For the Coulomb interaction in quantum wires see e.g.:
R. Loudon, Am. J. Phys. 44, 1064 (1976)
L. Banyai, I. Galbraith, C. Ell, and H. Haug, Phys. Rev. B36, 6099 (1987)
PROBLEMS
Problem 7.1: Use the Hamiltonian (7.29) and the Hartree–Fock wave
function (7.34) to compute the ground-state energy with the 3D and the
2D Coulomb interaction potentials, respectively. Hint: Use the expansion
in terms of Legendre polynomials
1
|k − k
|
2
=
1
k
2
n,n
k
k
n+n
P
n
(cos θ)P
n
(cos θ) for k
<k
=
1
k
2
n,n
k
k
n+n
P
n
(cos θ)P
n
(cos θ) for k<k
1
|k − k
|
=
1
k
n
k
k
n
P
n
(cos θ) for k
<k
=
1
k
n
k
k
n
P
n
(cos θ) for k<k
and the integrals

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Interacting Electron Gas 127
1
−1
d cos θP
n
(cos θ)P
n
(cos θ)=
2
2n +1
δ
n,n
2π
0
dθ P
n
(cos θ)=2π
1
2
n
n
n/2
2
for n even
=0 for n odd .
Problem 7.2: Compute the pair correlation function (7.50) for the 3D
and 2D case. Prove that R
ss
(r − r
) → 0 for r → r
.
Problem 7.3: Evaluate the Coulomb matrix elements for the two lowest
subbands of a infinitely high quantum well confinement potential.
Problem 7.4: Compute the properly normalized envelope wave function
corresponding to the lowest eigenvalue for a quantum wire of radius R and
infinite confinement barriers.
This page intentionally left blank
