Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


Part VIII
-----_
Lie Groups and Their
Applications

1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
I

27 _
Lie
Groups
and
Lie Algebras
The theory
of
differential equations had flourished to snch a level by the 1860s that
a systematic study of their solutions became possible. Sophus Lie, a Norwegian
mathematician, undertook such a study using the same tool that was developed by
Galois and others to study algebraic equations: group theory. The groups associ-
ated with the study of differential equations, now called Lie groups, unlike their
algebraic counterparts, are uncountably infinite, and, as such, are both intricate
and full of far-reaching structures.
It
was beyond the wildest dream of any 19th-
century mathematician to imagine that a concept as abstract as Lie groups would
someday find application in the study of the heart of matter. Yet, three of the four
fundamental interactions are described by Lie groups, and the fourth one, gravity,
is described in a language very akin to the otherthree.
27.1 Lie Groupsand Their Algebras
Lie groups are infinite groups that have the extra property that their multiplication
law is differentiable. We have seen that the natural setting for differentiation is the
structure of a manifold. Thus, Lie groups must have manifold properties as well
as group properties.
Lie
groups
defined
27.1.1. Definition. A
Lie
group G is a differentiable manifold endowed with a
group structure such that the group operation G x G
-+
G
and
the map G
-+
G
given by g
>-+
g-l
are differentiable.
If
the dimension
of
the underlying manifold
is r, we say that G is an r-parameterLie group.
Because of the dual nature
of
Lie groups, most
of
their mapping properties
combine those
of
groups and manifolds.
For
instance, a Lie
group
homomor-

816
27. LIE
GROUPS
AND
LIE
ALGEBRAS
phism
is a
group
homomorphism
that
is
also
e
oo
,
and
a
Lie
group
isomorphism
is a
group
isomorphism
that
is
also
a
diffeomorphism.
27.1.2.
Example.
GL(V)
IS
A LIEGROUP
GL(V)
isa
Lie
group As the paradigm
of
Lie groups, we consider
GL(V),
the set of invertible operators on an
n-dimensional real vector space
'\7,
and show that it is indeed a Lie group. The set
L(V)
is a vector space
of
dimension n
2
(Proposition 25.1.1), and Iherefore, by Example 26.1.7,
a manifold of the same dimension. The map det : C(V)
-+
IR is a e
oo
map because
the determinant, when expressed in terms
of
a matrix, is a polynomial.
In
particular, it is
continuous. Now note that
GL(V)
= deCI(1R -
{O))
and that R -
{O}
is open.
It
follows Ihat
GL(V)
is an
open
submanifold
of
£,(V). Thus,
G
L(V)
is an n
2
-dimensionalmanifold.ChoosingabasisB forVandrepresentingoperators
(points) A
of
GL(V) as matrices
(aij)
in Ihat basis provides a coordinate patchfor GL(V).
We denote this coordinate patch
by
{xU},
where x
ij
(A) =
aij'
To show Ihat
GL(V)
is a Lie group, we
need
to prove Ihat
if
A, B E
GL(V),
Ihen
AB :
GL(V)
x
GL(V)
-+
GL(V)
and
A-I:
GL(V)
-+
GL(V)
P(aij)
= a polynomial in
aij.
are e
oo
maps
of
manifolds. This is done by showing that the coordinate representations
of
.
these maps are e
oo
.Theserepresentations are simplythe matrixrepresentationsof operators.
Since ASis a linearfunction
of
elements
of
the two matrices, it has derivatives
of
all orders.
It
follows that AS is e
oo
. The case
of
A-I
is only slightly more complicated. We note that
A-I
=
P(aU)
detA '
Thus, since detA is also a polynomial
in
aij,
the kth derivative
of
A-I
is
of
the form
Q(aij)/(detA)k,
where Q is anoIher polynomial. The fact that detA # 0 establishes Ihe
e
oo
property
of
A-I.
One can similarly show that
if
V is a complex vector space, then
GL(V)
is a manifold
of
dimension 2n
2.
III
27.1.3.
Example.
SL(V)
IS A LIEGROUP
SL(V)is a
Lie
group Recall that
SL(V)
is Ihe subgroup
of
GL(V)
whose elementshave unit determinant. Since
det:
GL(V)
-+
IR
is e
oo
,
Theorem 26.3.7 and the example after it show Ihat
SL(V)
=
det"
1
(I)
is a submanifold
of
GL(V)
of
dimensiondim
GL(V)
-dim
IR= n
2
-I.
Since it is
already a subgroup, we conclude Ihat SL(V)
isalso a Lie group (Problem 27.5). Similarly,
when V is a complex vector space, one can show that dim
SL(V)
=2n
2
- 2 III
27.1.4.
Example.
OrnER
EXAMPLES
OF LIEGROUPS
The reader may verify Ihe following:
(a) Any finite-dimensional vector space is a
Lie
group under vector addition.
(b) The unit circle
SI,
as a subset
of
nonzero multiplicative complex numbers is a Lie
group under multiplication.
(c) The product G x
H
of
two Lie groups is itselfa
Lie
group wiIh Ihe product manifold
structure and the direct product group structure.
(d) G
L (n,
JR.),
the set
of
invertiblen x n matrices,is
aLie
group undermatrixmultiplication.

group
of
affine
motions
ofR
n
local
Lie
groups
27.1 LIE
GROUPS
ANO
THEIR
ALGEBRAS
817
(e) Let G = GL(n, R} x R" be the product manifold. Definethe group operatiouby
(A,
u)(B,v)
==
(AB,
Av+u). The reader may verify that this operatiouindeed
defiues
a
group structure on G. Infact, G becomes a Lie group, calledthe
group
of affine
motions
of
R",
for if we identify (A,u) with the affine motion! x
1---*
Ax +u of
R",
then the
group operation in G is composition of affine motions. We shall study in some detail the
poincare
group,
asubgroup
of the
group
of
affine
motions,
in
which
the
matrices
are(pseudo)
orthogoual. III
In
calculations, one translates all group operations to the corresponding op-
erations
of
charts. This is particularly useful
when
the group multiplication
can
be defined ouly locally. One then speaks
of
an r-parameter local
Lie
group. To
be precise, one considers a neighborhood
U
of
the origin
of
lll.' and defines an
associative "multiplication" m : U x U
---+
R" and an inversion i : Uo
---+
U
where Uo is a subset
of
U. We therefore write the multiplication as
m(a,
b) = c, a, b, C E IR
Y
,
where a =
(0
1,
0
2,
...
,
or),
etc. are coordinates
of
elements
of
G.
The
coordinates
of
the identity element
of
G are taken to be all zero. Thus,
m(a,
0) = a and
m(a,
i(a))
=
O.
In
component forms,
k = 1,2,
...
,r. (27.1)
x,y
E U.
local
group
of
transformations
The fact that G is a manifold implies that all functions in Equation (27.1) are
infinitely differentiable.
27.1.5.
Example.
As an example of a loca11-parameter Lie group, consider the multi-
plicationrulem : U x U
-+
lll.
whereU = (x E
lll.llxl
< I) and
2xy
-x
- y
m(x,
y) =
I'
xy
-
The reader can checkthat
m(x,
(y, z)) =
m«x,
y), z), so.that the multiplication is asso-
ciative.
Moreover,m(O,x) = m(x,O) = x for all x E U, andi(x) =
x/(2x
-i),
defined
forUO
= (x E
lll.llxl
<
!).
III
27.1.1 Group Action
As mentioned in our discussion
of
finite groups, the action
of
a group on a set is
more easily conceived than abstract groups.
In
the case
of
Lie groups, the natural
action is not on an arbitrary set, but on a manifold.
27.1.6. Definition,
Let
M be a manifold. A local
group
of
transformations
acting
on M is a (local) Lie group
G, an (open) subset U
with
the property leJ x M C
U c G x
M,
and
a
map
\jI : U
--+
M satisfying the following conditions:
IThese consist of a linear transformation followed by a translation.

818
27. LIE
GROUPS
AND
LIE
ALGEBRAS
M
Figure 27.1 For small regions of
M.
we may be able to include a large portionof G.
However,
if
we
want
to
include
allof
M,
aswe
should,
then
onlya small
neighborhood
of
theidentitymaybe
available.
1.
If(g,
P) E U, (h, 1jI(g,
P))
E U,
and
(hg, P) E U, then
1jI(h,W(g,
P))
= W(hg,
Pl.
2.
Wee,
P) = P for all P E M.
3.
1f(g,
P) E U, then
(g-I,
1jI(g,
P))
E U
and
W(g-I,
W(g,
P))
= P.
Normally, we shall denote W(g, P) by
g.
P, or gP, Then the conditions
of
the definition above take the simple
fonn
g.
(h . P) = (gh) . P, g, h E G, P
EM,
e » P = P for all P E M,
g-1
. (g . P) = P, g E G, P
EM,
(27.2)
orbit;
transitive
action;
stabilizer
whenever g . P is defined. Note that the word "local" refers to G and not M, i.e.,
we may have to choose a very small neighborhood of the identity before all the
elements
of
that neighborhood can act on all points
of
M (see Figure 27.1).
All the properties of a group action described in Chapter 23 can be applied
here as well. So, one talks about the
orbit
of G as the collection of points in M
obtainedfrom one anotherby the action of G; a
transitive
action of G on M when
there is only one orbit; the
stabilizer
of a pointof
M,
etc. The only extracondition
one has to be aware of is that the group action is not defined for all elements of G,
and that a sufficiently small neighborhood
of
the identity needs to be chosen.
In the old literature, the group action is described in terms of coordinates.
Although for calculations this is desirable, it can be very clumsy for formal dis-
cussions, as we shall see
later.
Let a = (a
l
,
...
,
ar)
be a coordinate system

27.1 LIE
GROUPS
AND
THEIR
ALGEBRAS
819
on G and x =
(r
',
...
,
x")
a coordinate system on M. Then the gronp action
'11
: G x M --> M becomes a set
of
n fnnctions described by
x!
= W(a, x), x" =Web, x') = W(m(b, a), x),
(27.3)
where
m is the mnltiplication law
of
the Lie gronp written
in
terms
of
coordinates
as given in Eqnation (27.1).
It
is assnmed
that'll
is infinitely differentiable.
27.1.7.
Box. Equation (27.3) can be used to unravel the multiplication law
for
the
lie
group when the latter is given in terms
of
transformations.
27.1.8.
Example.
EXAMPLES OF GROUPS OF TRANSFORMATION
(a) Thetwo-dimensional
rotation
group
actsonthexy-planeas
<1>(0,
r)
= (x cos a- y sinO, x sinO + y cosO).
If
we write
r'
=
<1>(01,
r) and r' =
<1>(02,
r'),
then a simple calculation shows that
r"
= (x cos(OI +02) - Ysin(O! +
02),
x sin(O! +02) +y cos(O!+
02)).
With
r"
= (m(O!, 02);
r),
we recognize the "multiplication"1aw as m(OI, 02) = 01 + 02.
The
orbits
are
circlescentered
at
the
origin.
(b) Let M =
JR
n
,
a a fixed vector in JR", and G = R Define
Ij/
:
JR
x
JR"
-+
JR"by
Ij/(t,
x) = x +ra,
x e R", t
ElR..
This group action is globally defined.
The
orbits are straightlines parallel to a. The group
translations
is thesetof translationsinthe
direction
a in
IR
n
.
The
reader
mayverify
that
the
"multipli-
cation"
law is
addition
of t's.
(c) Let G =
lR+
be themultiplicative
group
of nonzeropositivereal
numbers.
Fix real
numbers
aI,
a'2
•...
, an, not allzero.Definetheactionof G on
lR
n
by
scale
transformations
one-dimensional
projective
group
The
orbits
are
obtained
by choosinga pointin
lR
n
and
applying
G to it for
different
A'S.
Theresultis a
Curve
inR". Forexample,
if
n = 2,
ct'l
= 1,and
ct'2
=2, weget, asthe
orbit
containing
xo
the
curve
YO
2
Y=2"x,
X
o
which is a parabola going through the origin and the point (xO,yO). Note that the orbit
containing
theoriginhasonlyone
point.
This
group
is calledthe
group
of scale transfor-
mations.The
multiplication
lawis
ordinary
multiplication of (positive) real
numbers.
(d) Let G =
JR4
acton
M =
JR
by

820
27. LIE
GROUPS
AND
LIE
ALGEBRAS
The reader may verify that this is indeed the action
of
a group (catch where the condition
ala4
'-aZa3
i=
Oisused!),
andifx'
= <p(b,
x)
and
x"
= <p(a,
x'),
then
n
(al
bl
+a2b3)x +
al
b:2
+a2
b4
x = ,
(a3bl +a4
b3)x
+a3b2 +a4
b4
so that the multiplication rule is
This group is called the one-dimensional projective group.
III
27.1.2 Lie Algebra of a Lie Group
The group property of a Lie group G provides a natural diffeomorphism on G that
determines a substantial part of its structure.
27.1.9. Definition.
Let
G be a Lie group
and
g E G. The
left
translation by g is
a diffeomorphism Lg :
G
->
G defined by
A vector field
eon
G is called left-invariant
iffor
each g E G, eis
L.-related
to
itself;
i.e}
lefltranslation,
left-invariant
vector
fields,
lefl-invariant
forms,
and
their
"right"
counterparts
Lg(h)
= gh
V
hE
G.
or
Lg.(e(h))
=
e(gh)
V g, h « G.
The set
of
left-invariantvector fields on G is denotedby g. A l-formwhose pairing
with a left-invariant vector field gives a constantfunction on G is called a left-
invariant l-form.
The right translation by g, R
g
:
G
->
G,
and
right-invariant vectorfields
and l-forms are defined similarly.
The reader may easily check that right and left translations commute:
V
g,h
E G
(27.4)
Moreover,
if
wi,
is a I-form on
~,(G),
then w E A
l(G),
given by wig sa
L;.IW
I
" is a left-invariant I-form:
independent
of
g.
It
is convenient to have a coordinate representation of L
g
•.
The
coordinaterepresentation of L
g is simply the multiplicationlaw Lg (h) = m(g,
h),
2When there is no danger of confusion, we shall use
~(h)
for
~Ih'
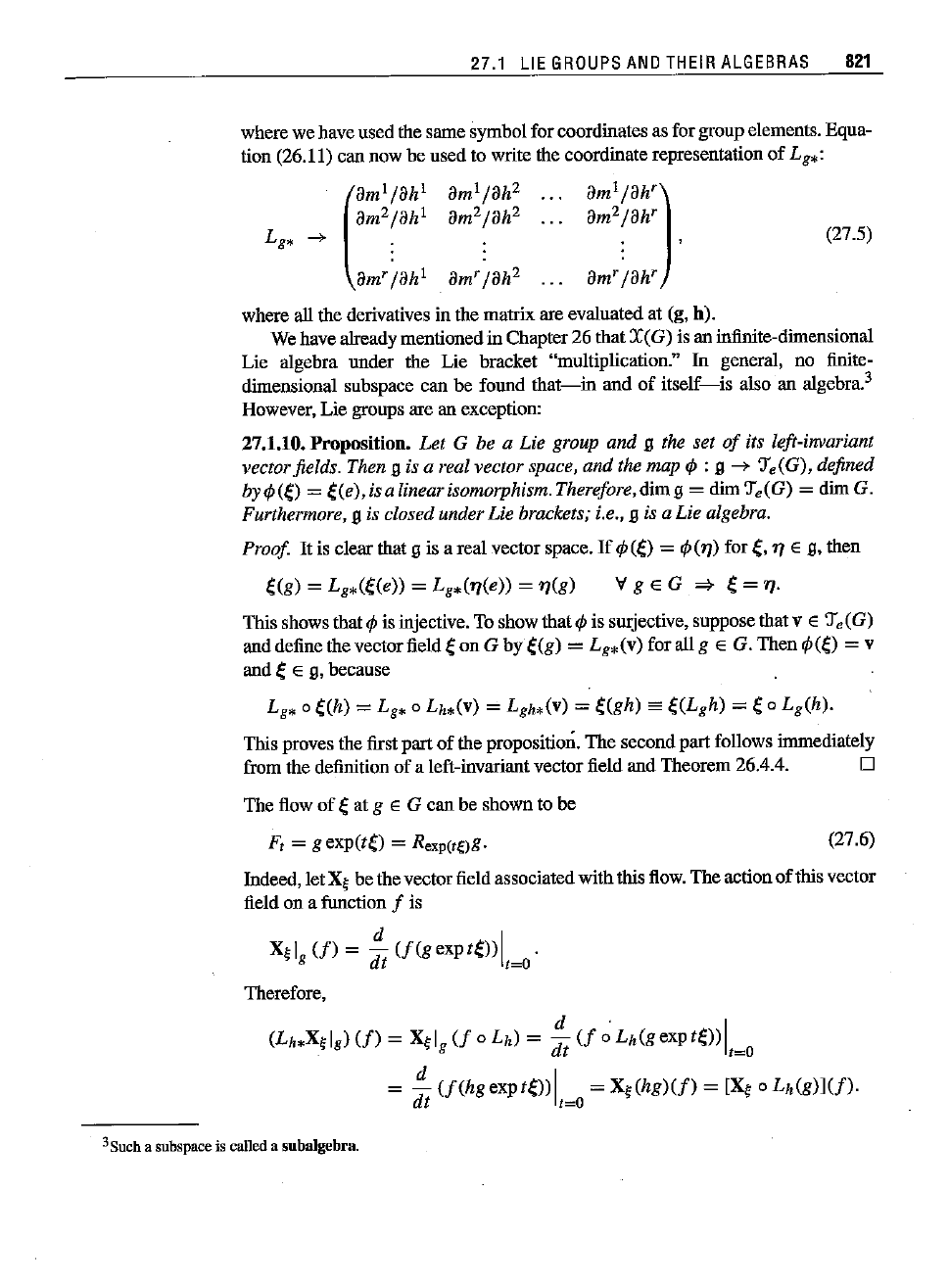
27.1 LIE
GROUPS
AND
THEIR
ALGEBRAS
821
where we have used the same symbol for coordinates as for group elements. Equa-
tion (26.11) can now be used to write the coordinate representation
of
L
g*:
(
am!
lah!
am
2/ah!
L
g
* --+ :
am'lah!
am!
lah']
am
2/ah'
. ,
am'lah'
(27.5)
where
all the derivatives in the matrix are evaluated at (g, h).
We have already mentionedin Chapter 26 that
X(
G) is an infinite-dimensional
Lie algebra under the Lie bracket ''multiplication.''
In
general, no finite-
dimensional subspace can be found
that-in
and
of
itself-is
also an algebra.'
However, Lie groups are an exception:
27.1.10. Proposition.
Let G be a Lie group and g the set
of
its left-invariant
vector fields. Then
g is a real vector space, and the map
</>
: g
--->
'Je(G), defined
by</>(~,)
= e(e),
isa
linearisomorphism. Therefore,dim g = dim'Je(G) =dim G.
Furthermore, g is closed under Lie brackets; i.e., g is a Lie algebra.
Proof
Ilis
clear that g is
areal
vector space.
If
</>
(e) =
</>(1/)
fore,
1/E g, then
v g E G
=>
e=1/.
This shows that
</>
is injective. To show that e is surjective, supposethat v E 'Je(G)
and define the vectorfield e on G by
e(g)
=Lg*(v) for all g E G. Then
</>(e)
=v
and
eE g, because
L
g*
0
e(h)
= L
g*
0 Lh*(V) = Lgh*(V) =
e(gh)
'"
e(Lgh)
=
eo
Lg(h).
This proves the first part
of
the proposition, The secondpart follows immediately
from the definition of a left-invariant vector field and Theorem 26.4.4. D
The flow
of
eat g E G can be shown to be
F
t
= g exp(te) = Rexp(telg.
(27.6)
Indeed, let
X, be the vectorfield associatedwiththis flow.The action
of
this vector
field on a function
f is
X,l
g
(f)
=
:t
(f(gexPte))lt~o'
Therefore,
d·
I
(Lh*X,lg)(f)
= X,l
g
(f
0 Lh) =
-d
(f
0
Lh(gexpteJ)
t t=O
=
dd
(f(hgexpteJ)1
=
X,(hg)(f)
=
[X;
0
Lh(g)](f).
t t=O
3S
uch
a
subspace
is calleda subalgebra.

822 27. LIE
GROUPS
AND
LIE
ALGEBRAS
The
Lie
algebra
01
a
Lie
group
Since this is true for all f and g, and
X~
Ie
= e(e), we conclude that
X~
is the
unique left-invariant vector field corresponding to
e(e).
27.1.11. Definition. The Lie algebra
of
the Lie group G is the Lie algebra 9
of
left-invariant vector fields on G. Sometimes we think
of
eas a vector in Te(G).
In that case, we denote by
X~
the left-invariant vector field whose value at the
identity
is
e-
The
isomorphism
of
9 with Te(G) induces a Lie bracket on Te(G) and turns
it into a Lie algebra. In many cases
of
physical interest, it is this interpretation
of
the Lie algebra
of
G that is most nseful.
If
two gronps stand in some algebraic
relationto one another, theirLiealgebraswill inherit such relations.Moreprecise!y,
let G and
H be Lie groups with Lie algebras 9 and
~,
respectively. Suppose
<P
: G
--+
H is a Lie gronp homomorphism.
Then
identifying 9 with Te(G) and
~
with Te(H), and using Theorem 26.4.4, we conclude that
<P.
: 9
--+
~
is a Lie
algebra homomorphism, i.e., it preserves the Lie brackets:
v
e,
rz
E g.
(27.7)
In particular,
if
c/>
is a Lie group isomorphism,then
c/>.
is aLie algebraisomorphism.
27.1.12.
Example.
LetVbeacomplexvectorspacewithitsgenerallineargroupGL(V),
a 2n
2
-dimensional Lie group. Recall that GL(V) is an open submanifold of ,c,(V). By
Equation
(26.4), 'Je(GL(V)) =
'Je(,c,(V)),
where e is the unit operator.
If
we identify
'Je(,c,(V))
with .c(V) [see the hox after Equation (26.4)], we may conclude that ,c,(V),
whichwedeooteby
g[(V)
in thepresentcontext,is the Lie algebraof GL(V) in whichthe
Lie
bracket
is the
commutator.
Weusethe
notation
ACt)
fora
curve
in GL(V) andAforthe
vectortangentto thecurve. III
It
is instructive to construct the coordinate representation
of
vector fields on
GL(V).
Let f :
GL(V)
--+
R be a function and Aa vector field. Then, we have
. d daij
af
A(f)
= dt
(f(A(t)))
=
dt
axij'
or,since f is arbitrary,
. daij a . a dA
A=
--
..
==aij-
..
==
-(t),
dt
ax'] ax']
dt
wheresummationover repeatedindices is understoodand we introduced
dA/
dt
as
anabbreviationfor tiij(a/ axij).However, the one-to-onecorrespondencebetween
matrices and operators makes this more than
just
an abbreviation. Indeed, we can
interpret
dA/dt
as the derivative
of
A and perform such differentiation whenever
it is possible.
The
equation above states that
27.1.13. Box.
To obtain the matrix elements (coordinates)
of
the operator
A,
one differentiates the t-dependent elements
of
the (matrix representation
of
the) operator A(t).
