Hancock G.J., Murray Th.M., Ellifritt D.S. Cold-Formed Steel Structures to the AISI Specification
Подождите немного. Документ загружается.

on a graph of buckling stress versus half-wavelength as
shown at point B in Figures 3.6 or 3.12. The buckling stress
may be replaced by a load for compression or a moment for
bending to simplify the calculations. The interaction
between the different elements is automatically accounted
for as it should be for such complex modes. Elastic buckling
solutions for edge-stiffened sections are given for compres-
sion members in Lau and Hancock (Ref. 3.8) and for
¯exural members in Schafer and Peko
È
z (Ref. 12.3) and
Hancock (Ref. 12.4), and can be used instead of the ®nite
strip method.
For the overall modes, the elastic buckling stresses
(F
e
) predicted by the simple formulae in Chapter C of the
AISI Speci®cation are used. The reason for using the AISI
Speci®cation rather than the ®nite strip analysis is that
boundary conditions other than simple supports are not
accounted for in the ®nite strip method. Further, for ¯ex-
ural members, moment gradient cannot be accounted for in
the ®nite strip method. By comparison, the design formulae
in the AISI Speci®cation can easily take account of end
boundary conditions using effective length factors and
moment gradient using C
b
factors as described in Section
C3.1.2 of the AISI Speci®cation.
12.3 STRENGTH DESIGN CURVES
12.3.1 Local Buckling
Local buckling direct strength curves for individual
elements have already been discussed and were included
in Figure 4.5 for stiffened compression elements and in
Figure 4.6 for unstiffened compression elements. The limit-
ing stress on the full plate element has been called the
effective design stress in these ®gures. The concept is that
at plate failure, either the effective width can be taken to be
at yield or the full width can be taken to be at the effective
design stress. This concept can be generalized for sections
Chapter 12
378

so that a limiting stress on the gross section, either in
compression or bending, can be de®ned for the local buck-
ling limit state. The resulting method is the direct strength
method. The research of Schafer and Peko
È
z (Ref. 12.1) has
indicated that the limiting stress (F
nl
) for local buckling of a
full section is given by
F
nl
F
y
for l
l
0:776 12:1
F
nl
1 ÿ 0:15
F
crl
F
y
!
0:4
0
@
1
A
F
crl
F
y
!
0:4
F
y
for l
l
> 0:776
where
l
l
F
y
F
crl
s
12:3
The 0.4 exponent in Eq. (12.2), rather than 0.5 as used in
the Von Karman and Winter formulae discussed in Chapter
4, re¯ect a higher post-local-buckling reserve for a complete
section when compared with an element. A comparison of
local buckling moments in laterally braced beams is shown
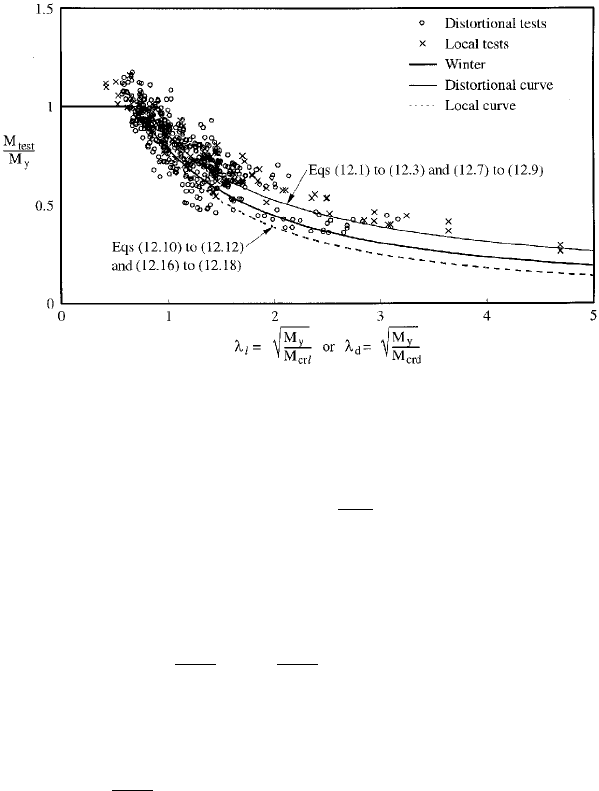
by the crosses () in Figure 12.1 compared with Eqs.
(12.1)±(12.3).
The local buckling limiting stress (F
nl
) can be multi-
plied with the full unreduced section area (A) for a column
or full unreduced section modulus (S
f
) for a beam to get the
local buckling column strength (P
nl
) or the local buckling
beam strength (M
nl
), respectively. The resulting alternative
formulations of Eqs. (12.1)±(12.3) in terms of load or
moment for compression or bending respectively are
For compression
P
nl
P
y
for l
l
0:776 12:4
P
nl
1 ÿ 0:15
P
crl
P
y
!
0:4
0
@
1
A
P
crl
P
y
!
0:4
P
y
for l
l
> 0:776 12:5
12:2
Direct Strength Method
379
where
l
l
P
y
P
crl
s
12:6
For bending
M
nl
M
y
for l
l
0:776 12:7
M
nl
1 ÿ 0:15
M
crl
M
y
!
0:4
0
@
1
A
M
crl
M
y
!
0:4
M
y
for l
l
> 0:776 12:8
where
l
l
M
y
M
crl
s
12:9
In these equations, the loads have been derived from the
stresses by multiplying by the full unreduced section area
(A) throughout, and the moments have been derived from
the stresses by multiplying by the full unreduced section
modulus (S
f
) throughout.
FIGURE 12.1 Laterally braced beams: bending data.
Chapter 12
380
12.3.2 Flange-Distortional Buckling
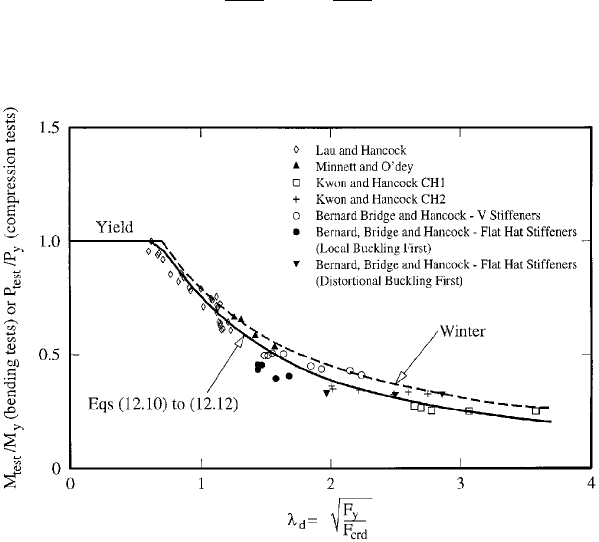
Flange-distortional buckling direct strength curves were
developed for sections in both compression and bending by
Hancock, Kwon, and Bernard (Ref. 12.2) and are shown in
Figure 12.2. Research has indicated that the limiting stress
(F
nd
) for distortional buckling of a full section is given by
Eqs. (12.10)±(12.12). A comparison of distortional buckling
loads and moments is shown in Figure 12.2 compared with
Eqs. (12.10) to (12.12).
F
nd
F
y
for l
d
0:561 12:10
F
nd
1 ÿ 0:25
F
crd
F
y
!
0:6
0
@
1
A
F
crd
F
y
!
0:6
F
y
for l
d
> 0:561
12:11
FIGURE 12.2 Comparison of distortional buckling test results
with design curves.
Direct Strength Method
381

where
l
d
F
y
F
crd
s
12:12
The 0.6 exponent in Eq. (12.11), rather than 0.4 as used for
local buckling strength in Eqs. (12.1) to (12.3), re¯ects a
lower postbuckling reserve for a complete section in the
distortional mode than the local mode.
The distortional buckling limiting stress (F
nd
) can be
multiplied with the full unreduced section area (A) for a
column or full unreduced section modulus (S
f
) for a beam to
get the distortional buckling column strength (P
nd
) or the
distortional buckling beam strength M
nd
. The resulting
alternative formulations in Eqs. (12.10)±(12.12) in terms of
load or moment for compression or bending, respectively,
are
For compression
P
nd
P
y
for l
d
0:561 12:13
P
nd
1 ÿ 0:25
P
crd
P
y
!
0:6
0
@
1
A
P
crd
P
y
!
0:6
P
y
for l
d
> 0:561
12:14
where
l
d
P
y
P
crd
s
12:15
For bending
M
nd
M
y
for l
d
0:561 12:16
M
nd
1 ÿ 0:25
M
crd
M
y
!
0:6
0
@
1
A
M
crd
M
y
!
0:6
M
y
for l
d
> 0:561 12:17
Chapter 12
382

where
l
d
M
y
M
crd
s
12:18
In these equations, the loads have been derived from the
stresses by multiplying by the full unreduced section area
(A) throughout, and the moments have been derived from
the stresses by multiplying by the full unreduced section
modulus (S
f
) throughout.
12.3.3 Overall Buckling
The overall buckling strength design curves are those
speci®ed in Section C of the AISI Speci®cation. For
compression members, they are described in Section 7.4
of this book and are shown in Figure 7.3. The design stress
(F
n
) for compression members is as speci®ed in Section C4
of the AISI Speci®cation. For ¯exural members, they are
described in Section 5.2.3 of this book and shown in Figure
5.8. The design stress (F
c
) for ¯exural members is speci®ed
in Section C3.1.2 of the AISI Speci®cation.
The design stress (F
n
) for compression members can be
multiplied with the full unreduced section area (A) to give
the inelastic long-column buckling load (P
ne
):
P
ne
AF
n
12:19
Similarly, the design stress (F
c
) for ¯exural members can be
multiplied with the full unreduced section modulus (S
f
)to
give the inelastic lateral buckling moment (M
ne
):
M
ne
S
f
F
c
12:20
12.4 DIRECT STRENGTH EQUATIONS
The direct strength method allows for the interaction of
local and overall buckling of columns by a variant of the
uni®ed approach described in Chapter 7 for compression
members. This is achieved simply by replacing P
y
in Eqs.
Direct Strength Method
383
(12.4)±(12.6) for local buckling by P
ne
from Eq. (12.19). The
resulting limiting load (P
nl
) as given by Eqs. (12.21)±(12.23)
accounts for the interaction of local buckling with overall
column buckling since the limiting load is P
ne
rather than
P
y
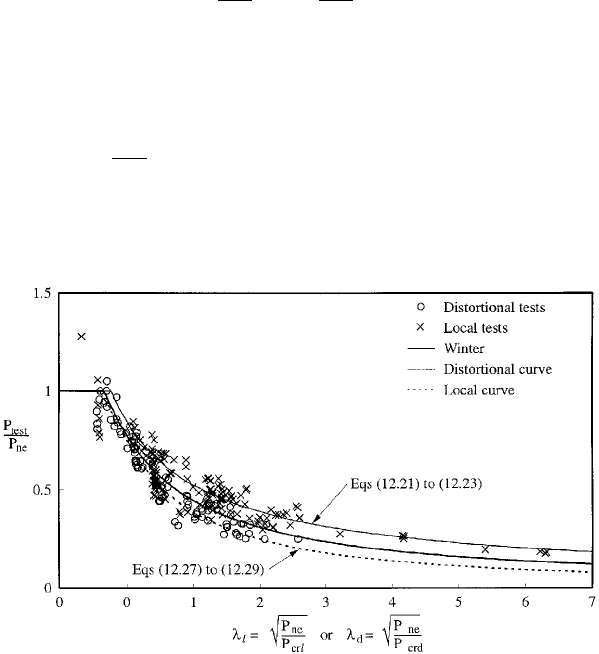
. A comparison of the test strengths for failure in the local
mode is shown by the crosses () in Figure 12.3 compared
with Eqs. (12.21)±(12.23).
P
nl
P
ne
for l
l
0:776 12:21
P
nl
1 ÿ 0:15
P
crl
P
ne
0:4
!
P
crl
P
ne
0:4
P
ne
for l
l
> 0:776
12:22
where
l
l
P
ne
P
crl
s
12:23
A similar set of equations can be derived for the
interaction of local and lateral buckling of beams, using a
FIGURE 12.3 Pin-ended columns: compression data.
Chapter 12
384

variant of the uni®ed approach described in Chapter 5 for
¯exural members. This is achieved simply by replacing M
y
in Eqs. (12.7) ±(12.9) for local buckling by M
ne
from Eq.
(12.20). The resulting limiting moment (M
nl
) as given by
Eqs. (12.24)±(12.26) accounts for the interaction of local
buckling with lateral buckling since the limiting moment is
M
ne
rather than M
y
.
M
nl
M
ne
for l
l
0:776 12:24
M
nl
1 ÿ 0:15
M
crl
M
ne
0:4
!
M
crl
M
ne
0:4
M
ne
for l
l
> 0:776 12:25
where
l
l
M
ne
M
crl
s
12:26
The direct strength method also allows for the inter-
action of distortional and overall buckling by a further
variant of the uni®ed approach. This is achieved simply
by replacing P
y
in Eqs. (12.13)±(12.15) for distortional
buckling by P
ne
from Eq. (12.19). The resulting limiting
load (P
nd
) as given by Eqs. (12.27)±(12.29) accounts for the
interaction of distortional buckling with overall column
buckling since the limiting load is P
ne
rather than P
y
.A
comparison of the test strengths for failure in the distor-
tional mode is shown by the circles (s) in Figure 12.3
compared with Eqs. (12.27)±(12.29).
P
nd
P
ne
for l
d
0:561 12:27
P
nd
1 ÿ 0:25
P
crd
P
ne
0:6
!
P
crd
P
ne
0:6
P
ne
for l
d
> 0:561 12:28
Direct Strength Method
385

where
l
d
P
ne
P
crd
s
12:29
A similar set of equations can be derived for the
interaction of distortional and lateral buckling of beams,
using a further variant of the uni®ed approach. This is
achieved simply by replacing M
y
in Eqs. (12.16)±(12.18) for
distortional buckling by M
ne
from Eq. (12.20). The resulting
limiting moment M
nd
as given by Eqs. (12.30)±(12.32)
accounts for the interaction of local buckling with lateral
buckling since the limiting moment is M
ne
rather than M
y
.
M
nd
M
ne
for l
d
0:561 12:30
M
nd
1 ÿ 0:25
M
crd
M
ne
0:6
!
M
crd
M
ne
0:6
M
ne
for l
d
> 0:561 12:31
where
l
d
M
ne
M
crd
s
12:32
The nominal member strength is the lesser of P
nl
and P
nd
for
compression members and of M
nl
and M
nd
for ¯exural
members. It has been suggested that the same resistance
factors and factors of safety apply as for normal compres-
sion and ¯exural member design.
12.5 EXAMPLES
12.5.1 Lipped Channel Column (Direct
Strength Method)
Problem
Determine the nominal axial strength P
n
of the lipped
channel in Example 7.6.3 by using the direct strength
Chapter 12
386
method. The geometry is shown in Figure 7.9 and the
dimensions in Example 7.6.3.
Solution
A. Compute the Elastic Local and Distortional Buckling
Stresses Using the Finite Strip Method
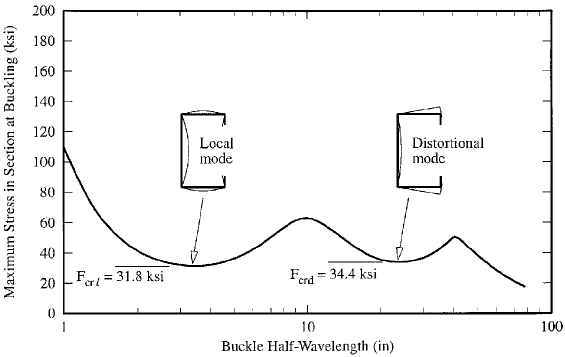
Program THIN-WALL (Ref. 11.3)
The elastic local (F
crl
) and distortional buckling stres-
ses are shown in Figure 12.4.
F
crl
31:8 ksi at 3.5-in. half-wavelength
F
crd
34:4 ksi at 24-in. half-wavelength
A 0:645 in
2
:
P
crl
AF
crl
0:645 31:8 20:51 kips
P
crd
AF
crd
0:645 34:4 22:2 kips
FIGURE 12.4 Lipped channel in compression.
Direct Strength Method
387
