Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 825

and positive real. Hence, He G(e

θ

) ≥ 0, θ ∈ [0, 2π]. Now, let (A, B, C, D)

be a minimal realization of G(z). Using T heorem 13.28, it follows from

(13.206)–(13.207) that

G(z) + G

∗

(z)

= C(zI

− A)

−1

B + D + B

∗

− A)

−T

+ D

= W

W + B

P B + (B

P A + W

L)(zI

− A)

−1

∗

− A)

−T

P B + L

W )

= W

W + W

L(zI

− A)

−1

B + B

∗

− A)

−T

∗

− A)

−T

[(z

∗

− A)

P (zI

− A) + (z

∗

− A)

P A

P (zI

− A)](zI

− A)

−1

= W

W + W

L(zI

− A)

−1

B + B

∗

− A)

−T

∗

− A)

−T

L + (|z| −

)P ](zI

− A)

−1

B. (13.222)

Now, suppose, ad absurdum, that He G(e

θ

) is not positive deﬁnite for all

θ ∈ [0, 2π]. Then, for some θ =

θ there exists x ∈ C

, x 6= 0, such that

∗

[He G(e

θ

)]x = 0. In this case, it follows from (13.222) that Bx = 0 and

W x = 0. Hence, x

∗

[He G(z)]x = 0 for all z ∈ C, and hence, det[He G(z)] ≡

0, which leads to a contradiction. Thus, He G(e

θ

) > 0, θ ∈ [0, 2π], which

proves the result.

13.13 Feedback Interconnections of Dissipative

Dynamical Systems

In this section, we consider feedb ack interconnections of dissipative dynam-

ical systems. Speciﬁcally, using the notion of dissipative and geometrically

dissipative dynamical systems, with appropriate storage functions and

supply rates, we construct Lyapunov functions for interconnected dynamical

systems by appropriately combining storage functions for each subsystem.

We begin by considering the nonlinear discrete-time dynamical system G

given by

x(k + 1) = f (x(k)) + G(x(k))u(k), x(0) = x

, k ∈ Z

, (13.223)

y(k) = h(x(k)) + J(x(k))u(k), (13.224)

where x ∈ R

, u ∈ R

, y ∈ R

, f : R

→ R

satisﬁes f (0) = 0, G :

→ R

n×m

, h : R

→ R

satisﬁes h(0) = 0, and J : R

→ R

l×m

, w ith the

nonlinear feedback system G

given by

(k + 1) = f

(k)) + G

(k), x

(k))u

(k), x

(0) = x

, k ∈ Z

(13.225)

(k) = h

(k), x

(k)) + J

(k), x

(k))u

(k), (13.226)

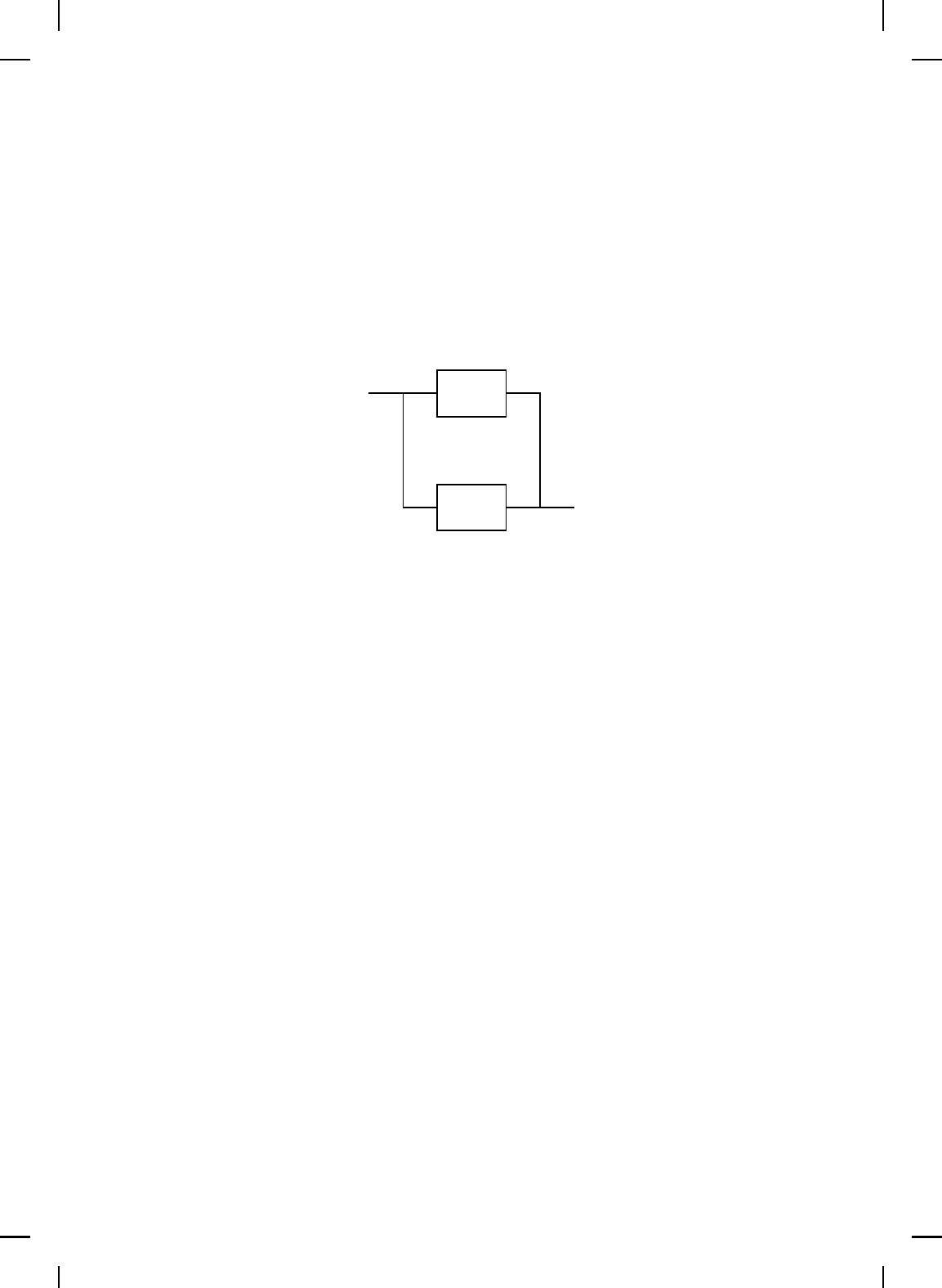
NonlinearBook10pt November 20, 2007

826 CHAPTER 13

where x

∈ R

, u

∈ R

, y

∈ R

, f

: R

→ R

satisﬁes f

(0) = 0,

: R

× R

→ R

×l

, h

: R

× R

→ R

satisﬁes h

(0) = 0, and

: R

× R

→ R

m×l

. Note that with the feedback interconnection given

by Figure 13.1, u

= y and y

= −u. The following results give suﬃcient

conditions for Lyapunov, asymptotic, and geometric s tability of the f eedback

interconnection given by Figure 13.1. For these results we assume that the

negative feedback interconnection of G and G

is well posed.



–

Figure 13.1 Feedback interconnection of G and G

Theorem 13.32. Consider th e closed-loop system consisting of the

nonlinear dynamical systems G given by (13.223) and (13.224) and G

given by (13.225) and (13.226) with input-output pairs (u, y) and (u

, y

respectively, and with u

= y an d y

= −u. Assume G and G

are zero

state observable and dissip ative with respect to the supply rates r(u, y)

and r

, y

) and with continuous positive deﬁnite radially unbounded

storage functions V

(·) and V

(·), respectively, such that V

(0) = 0 and

(0) = 0. Furthermore, assume there exists a scalar σ > 0 such that

r(u, y) + σr

, y

) ≤ 0. Then the following statements hold:

i) The negative feedback interconnection of G an d G

is Lyapunov s table.

ii) If G

is geometrically dissipative with respect to supply rate r

, y

)

and rank[G

, 0)] = m, u

∈ R

, then the negative feedback

interconnection of G and G

is globally asymptotically stable.

iii) If G and G

are geometrically dissipative w ith respect to supply rates

r(u, y) and r

, y

), respectively, V

(·) and V

(·) are such that there

exist constants α, α

, β, β

> 0 such that

αkxk

≤ V

(x) ≤ βkxk

, x ∈ R

, (13.227)

≤ V

) ≤ β

, x

∈ R

, (13.228)

then the negative feedback interconnection of G and G

is globally

geometrically stable.

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 827

Proof. i) Consider the Lyapunov function candidate V (x, x

) =

(x) + σV

). Now, the corresponding Lyapunov diﬀerence is given by

∆V (x, x

) = ∆V

(x) + σ∆V

) ≤ r(u, y) + σr

, y

) ≤ 0,

(x, x

) ∈ R

× R

which implies that the negative feedback interconnection of G and G

Lyapunov s table.

ii) Next, consider the Lyapunov function candidate V (x, x

) = V

(x)+

σV

). If G

is geometrically dissipative it follows that for some scalar

> 1,

∆V (x, x

) = ∆V

(x) + σ∆V

)

≤ −σ

− 1

) + r(u, y) + σr

, y

)

≤ −σ

− 1

), (x, x

) ∈ R

× R

Next, let R

△

= {(x, x

) ∈ R

× R

: ∆V (x, x

) = 0} and, since V

)

is positive deﬁnite, n ote that ∆V (x, x

) = 0 only if x

= 0. Now, since

rank[G

, 0)] = m, u

∈ R

, it follows that on every invariant set M

contained in R, u

(k) = y(k) ≡ 0, and hence, x(k + 1) = f(x(k)). Now,

since G is zero-state observable it follows that M = {(0, 0)} is the largest

invariant set contained in R. Hence, it follows from Theorem 13.5 that

(x(k), x

(k)) → M = {0, 0} as k → ∞. Now, global asymptotic stability of

the negative feedback interconnection of G and G

follows fr om the fact that

(·) and V

(·) are, by assumption, radially unbounded.

iii) Finally, consider the L yapunov function candidate V (x, x

) =

(x) + σV

). Since G and G

are geometrically dissipative it follows

that

∆V (x, x

) = ∆V

(x) + σ∆V

)

≤ −

ρ − 1

(x) − σ

− 1

) + r(u, y) + σr

, y

)

≤ −min



ρ − 1

− 1



V (x, x

), (x, x

) ∈ R

×R

which implies that the negative feedback interconnection of G and G

globally geometrically stable.

The next result presents Lyapun ov, asymptotic, and geometric stabil-

ity of dissipative feedback systems with quadratic supp ly rates.

Theorem 13.33. Let Q ∈ S

, S ∈ R

l×m

, R ∈ S

, Q

∈ S

, S

∈ R

m×l

NonlinearBook10pt November 20, 2007

828 CHAPTER 13

and R

∈ S

. Consider the closed-loop system consisting of the nonlinear

dynamical systems G given by (13.223) and (13.224), and G

given by

(13.225) and (13.226), and assume G and G

are zero-state ob s ervable.

Furth ermore, assume G is dissipative with respect to the quadratic supply

rate r(u, y) = y

Qy + 2y

Su + u

Ru and has a continuous radially

unbounded storage function V

(·) and G

is dissipative with respect to the

quadratic supply rate r

, y

) = y

+ 2y

+ u

and has a

continuous radially unboun ded storage function V

(·). Finally, assume there

exists σ > 0 such that

△



Q + σR

−S + σS

−S

+ σS

R + σQ



≤ 0. (13.229)

Then the following statements hold:

i) The negative feedback interconnection of G an d G

is Lyapunov s table.

ii) If G

is geometrically dissipative with respect to supply rate r

, y

)

and rank[G

, 0)] = m, u

∈ R

, then the negative feedback

interconnection of G and G

is globally asymptotically stable.

iii) If G and G

are geometrically d issipative with r espect to supply

rates r(u, y) and r

, y

) and there exist constants α, β, α

, β

> 0

such that (13.227) and (13.228) hold, then the negative feedback

interconnection of G and G

is globally geometrically stable.

iv) If

Q < 0, then the negative feedback interconnection of G and G

globally asymptotically stable.

Proof. Statements i)–iii) are a d irect consequence of Theorem 13.32

by noting

r(u, y) + σr

, y

) =









and h en ce, r(u, y) + σr

, y

) ≤ 0.

To show iv) consider the Lyapunov function candidate V (x, x

) =

(x) + σV

). Now, the corresponding Lyapunov diﬀerence is given by

∆V (x, x

) = ∆V

(x) + σ∆V

)

≤ r(u, y) + σr

, y

)

= y

Qy + 2y

Su + u

Ru + σ(y

+ 2y

+ u

)









≤ 0,

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 829

which implies that the negative feedback interconnection of G and G

Lyapunov stable. Now, the proof of global asymptotic stability of the closed-

loop system is identical to that of the continuous-time case given in Theorem

6.2 and, hence, is omitted.

The following corollaries are a direct consequence of Theorem 13.33.

For both results note that if a nonlinear dynamical system G is dissipative

(respectively, geometrically d iss ipative) with respect to a supply rate

r(u, y) = u

y − εu

u − ˆεy

y, where ε, ˆε ≥ 0, then with κ(y) = ky, where

k ∈ R is such that k(1 − εk) < ˆε, r(u, y) = [k(1 − εk) − ˆε]y

y < 0, y 6= 0.

Hence, if G is zero-state observable it follows from Theorem 13.21 that all

storage functions (respectively, geometrically storage functions) of G are

positive deﬁnite. For the next result, we assume that all storage functions

of G and G

are continuous.

Corollary 13.16. Consider the closed-loop system consisting of the

nonlinear d ynamical systems G given by (13.223) and (13.224) and G

given

by (13.225) and (13.226), and assume G and G

are zero-state observable.

Then the following statements hold:

i) I f G is passive, G

is geometrically passive, and rank[G

, 0)] = m,

∈ R

, th en the negative feedback interconnection of G and G

asymptotically stable.

ii) If G and G

are geometrically passive with storage fun ctions V

(·) and

(·), respectively, such that (13.227) and (13.228) hold, then the

negative feedback interconnection of G and G

is geometrically stable.

iii) If G is nonexpansive with gain γ > 0, G

is geometrically nonexpansive

with gain γ

> 0, rank[G

, 0)] = m, and γγ

≤ 1, then the negative

feedback interconnection of G and G

is asymptotically stable.

iv) If G and G

are geometrically nonexpansive with storage functions

(·) and V

(·), respectively, such that (13.227) and (13.228) hold,

with gains γ > 0 and γ

> 0, respectively, such that γγ

≤ 1, then the

negative feedback interconnection of G and G

is geometrically stable.

v) If G is passive and G

is inpu t-output strict passive then the negative

feedback interconnection of G and G

is asymptotically stable.

vi) If G and G

are input strict passive th en the negative feedback

interconnection of G and G

is asymptotically stable.

vii) If G and G

are output strict passive then the negative feedback

interconnection of G and G

is asymptotically stable.

NonlinearBook10pt November 20, 2007

830 CHAPTER 13

Proof. The proof is a direct consequence of Theorem 13.33. Speciﬁ-

cally, i) and ii) follow from Theorem 13.33 with Q = Q

= 0, S = S

= I

and R = R

= 0, while iii) and iv) follow from Theorem 13.33 with Q = −I

S = 0, R = γ

, Q

= −I

, S

= 0, and R

= γ

. Statement v) follows

from Theorem 13.33 with Q = 0, S = I

, R = 0, Q

= −ˆεI

, S

= I

and R

= −εI

, where ε, ˆε > 0. Statement vi) follows from T heorem 13.33

with Q = 0, S = I

, R = −εI

, Q

= 0, S

, and R

= −ˆεI

, where

ε, ˆε > 0. Finally, vii) follows from Theorem 13.33 w ith Q = −εI

, S = I

R = 0, Q

= −ˆεI

, S

= I

, and R

= 0, where ε, ˆε > 0.

Corollary 13.17. Consider the closed-loop system consisting of the

nonlinear dynamical systems G given by (13.223) and (13.224), and G

given

by (13.225) and (13.226). Let a, b, a

, b

, δ ∈ R b e such that b > 0, 0 < a +b,

0 < 2δ < b−a, a

= a+δ, and b

= b+δ, let M ∈ R

m×m

be positive deﬁnite,

and assu me G and G

are zero-state observable. If G is dissipative with

respect to the supply rate r(u, y) = u

My +

a+b

My +

a+b

Mu and has

a continuous radially unbounded storage function and G

is dissipative with

respect to the supply rate r

, y

) = u

−

and has a continuous radially unbounded storage function, then the negative

feedback interconnection of G and G

is globally asymptotically stable.

Proof. The proof is identical to that of the continuous-time case given

in Corollary 6.2 and, hence, is omitted.

13.14 Stability Margins of Discrete Regulators

In this section, we develop s uﬃcient conditions for gain, sector, and

disk margin guarantees for discrete-time nonlinear systems controlled by

nonlinear feedback regulators. To consider relative stability margins for

nonlinear discrete-time regulators consider the nonlinear system G given by

x(k + 1) = f (x(k)) + G(x(k))u(k), x(0) = x

, k ∈ Z

, (13.230)

y(k) = −φ(x(k)), (13.231)

where φ : R

→ R

is such that G is asymptotically stable with u = −y.

Furth ermore, assume that the system G is zero-state observable. The

following results provide algebraic suﬃcient cond itions that guarantee disk

margins for the nonlinear dynamical system G given by (13.230) and

(13.231).

Theorem 13.34. Consider the nonlinear dynamical system G given by

(13.230) and (13.231). Let α, β ∈ R be such that 0 < α ≤ 1 ≤ β < ∞.

Suppose there exists a positive-deﬁnite diagonal matrix Z ∈ R

m×m

and

there exist functions V

: R

→ R, P

: R

→ R

1×m

, P

: R

→ N

ℓ : R

→ R

, and W : R

→ R

p×m

such that V

(·) is continuous, V

(0) = 0,

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 831

(x) > 0, x ∈ R

, x 6= 0, and for all x ∈ R

, (13.137) holds and

0 = V

(f(x)) − V

(x) −

αβ

α+β

(x)Zφ(x) + ℓ

(x)ℓ(x), (13.232)

0 = P

(x) + φ

(x)Z + 2ℓ

(x)W(x), (13.233)

0 =

α+β

Z − P

(x) − W

(x)W(x). (13.234)

Then the nonlinear system G has a structured disk margin (α, β). Alter-

natively, if (13.232)–(13.234) are satisﬁed with Z = I

, then the nonlinear

system G has a disk margin (α, β).

Proof. The proof is identical to that of the continuous-time case given

in Theorem 6.5 and, hence, is omitted.

Corollary 13.18. Consider the nonlinear system G given by (13.230)

and (13.231). Let α, β ∈ R be su ch that 0 < α ≤ 1 ≤ β < ∞. Suppose there

exist a positive-deﬁnite diagonal matrix Z ∈ R

m×m

, fu nctions P

: R

→

1×m

, P

: R

→ N

, and a continuous function V

: R

→ R such that

(0) = 0, V

(x) > 0, x ∈ R

, x 6= 0, and for all x ∈ R

, (13.137) holds and

0 <

α+β

Z − P

(x), (13.235)

0 ≥ V

(f(x)) − V

(x) −

αβ

α+β

(x)Zφ(x)

(φ

(x)Z + P

(x))(

α+β

Z − P

(x))

−1

(φ

(x)Z + P

(x))

(13.236)

Then the nonlinear system G has a structured d isk margin (α, β). Alterna-

tively, if (13.235) and (13.236) are satisﬁed with Z = I

, then the nonlinear

system G has a disk margin (α, β).

Proof. It follows from Theorem 13.21 that (13.232)–(13.234) are

equivalent to (13.236). Now, the result is a direct consequence of Theorem

13.34.

The following theorem gives the nonlinear version of the results of

[262].

Theorem 13.35. Consider the nonlinear dynamical system G given

by (13.230) and (13.231). Let α, β ∈ R be such that 0 < α ≤ 1 ≤ β <

∞. Suppose there exist a positive-deﬁnite diagonal matrix Z ∈ R

m×m

, a

continuous function V : R

→ R,

: R

→ R

1×m

: R

→ N

, and a

scalar q > 0, and for all x ∈ R

, (13.137) holds and

0 < qI −

(x), (13.237)

0 ≥ V (f(x)) − V (x) −

αβ

q(α+β)

(x)Z

−1

(x). (13.238)

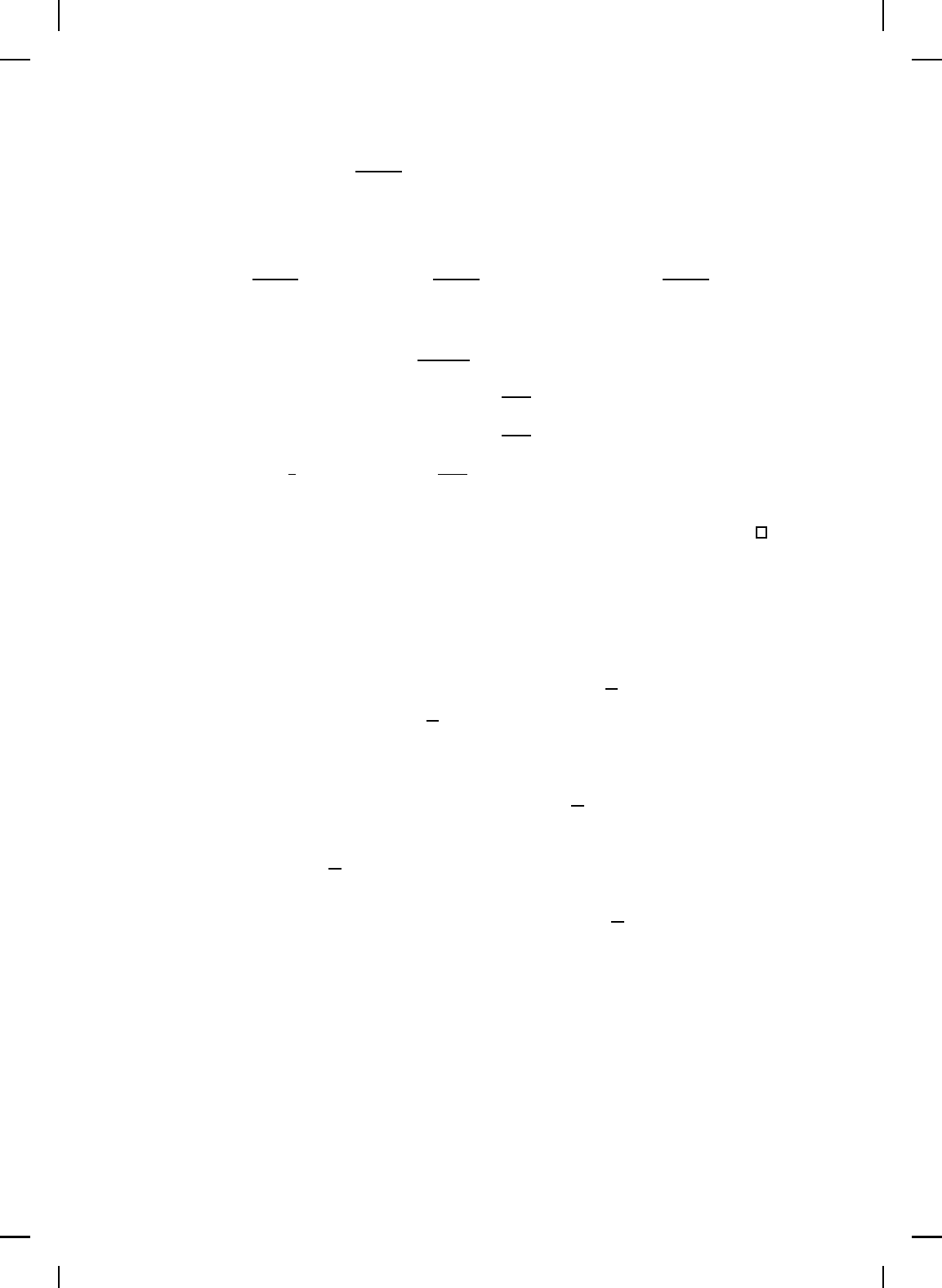
NonlinearBook10pt November 20, 2007

832 CHAPTER 13

Then, with φ(x) = −

q(α+β)

−1

(x)V

′T

(x), the nonlinear system G h as

a structured disk margin (α, β). Alternatively, if (13.238) is satisﬁed with

Z = I

, then the nonlinear system G has a disk margin (α, β).

Proof. The result is a direct consequence of Corollary 13.18 with

(x) =

q(α+β)

V (x), P

(x) =

q(α+β)

(x), and P

(x) =

q(α+β)

(x).

Speciﬁcally, since φ(x) = −Z

−1

(x) ·

(x) it follows from (13.238) that

for all x ∈ R

0 ≥ V (f(x)) − V (x) −

αβ

q(α+β)

(x)P

(x)

= q(α + β)



(f(x)) −V

(x) −

αβ

α+β

(x)φ(x)



= q(α + β)



(f(x)) −V

(x) −

αβ

α+β

(x)φ(x)

(φ(x) +

(x))

(

α+β

I −

(x))

−1

(φ(x) +

(x))



which implies (13.236), so that all the conditions of Corollary 13.18 are

satisﬁed.

13.15 Control Lyapunov Functions for Discrete-Time Sy stems

In this section, we consider a feedback control problem and introduce the

notion of control Lyapun ov functions for discrete-time systems. Consider

the controlled discrete-time nonlinear dynamical system given by

x(k + 1) = F (x(k), u(k)), x(t

) = x

, k ∈ Z

, (13.239)

where x(k) ∈ D ⊆ R

, k ∈ Z

, is the state vector, D is an open set

with 0 ∈ D, u(k) ∈ U ⊆ R

is the control input, and F : D × U → R

satisﬁes F (0, 0) = 0. We assume that the control input u(·) ∈ U in (13.239)

is restricted to the class of admissible controls consisting of measurable

functions u(·) ∈ U such that u(k) ∈ U for all k ∈ Z

, where the constraint

set U is given with 0 ∈ U. A mapping φ : D → U satisfying φ(0) = 0 is

called a control law. Furth ermore, if u(k) = φ(x(k)), where φ is a control

law and x(k), k ∈ Z

, satisﬁes (13.239), then u(·) ∈ U is called a feedback

control law. With u(k) = φ(x(k)) the closed-loop system is given by

x(k + 1) = F (x(k), φ(x(k)), x(0) = x

, k ∈ Z

. (13.240)

The following two deﬁnitions are required for s tating the results of this

section.

Deﬁnition 13.18. Let φ : D → U be a mapping on D\{0} with φ(0) =

0. Then (13.239) is feedback asymptotically stabilizable if the zero solution

x(k) ≡ 0 of the closed-loop s ystem (13.240) is asymptotically stable.

NonlinearBook10pt November 20, 2007

DISCRETE-TIME THEORY 833

Deﬁnition 13.19. Consider the controlled discrete-time nonlinear

dynamical system given by (13.239). A continuous positive-deﬁnite function

V : D → R satisfying

inf

u∈U

V (F (x, u)) < V (x), x ∈ D, x 6= 0, (13.241)

is called a control Lyapunov f unction.

Note that it follows from (13.241) that there exists a feedback control

law φ : D → U such that V (F(x, φ(x)))−V (x) < 0, x ∈ D, x 6= 0, and hence,

Theorem 13.2 implies that if there exists a control Lyapunov function for the

nonlinear dynamical system (13.239), then there exists a feedback control

law φ(x) such that the zero solution x(k) ≡ 0 of the closed-loop nonlinear

dynamical system (13.239) is asymptotically stable. Conversely, if there

exists a feedback control law u = φ(x) such that th e zero solution x(k) ≡ 0

of the nonlinear dynamical system (13.239) is asymp totically stable, then it

follows from Theorem 13.6 that there exists a continuous positive-deﬁnite

function V : D → R such that V (F (x, φ(x))) − V (x) < 0, x ∈ D, x 6= 0,

or, equivalently, there exists a control Lyapunov function for the nonlinear

dynamical system (13.239). Hence, a given nonlinear dynamical system of

the form (13.239) is feedback asymptotically stabilizable if and only if there

exists a control Lyapunov function satisfying (13.241). Finally, in the case

where D = R

and U = R

the zero solution x(k) ≡ 0 to (13.239) is globally

asymptotically stabilizable if and only if V (x) → ∞ as kxk → ∞.

Next, we consider the special case of nonlinear aﬃne systems in the

control and construct state feedback controllers that globally asymptotically

stabilize the zero solution of the nonlinear dynamical system under the

assumption that the sys tem has a radially unbou nded control Lyapunov

function. Speciﬁcally, we consider nonlinear aﬃne systems of the f orm

x(k + 1) = f (x(k)) + G(x(k))u(k), x(t

) = x

, k ∈ Z

, (13.242)

where f : R

→ R

is continuous and s atisﬁes f(0) = 0, and G : R

→ R

n×m

is continuous. For the n on linear s ystem G we assume that there exists a

two-times continuously diﬀerentiable control Lyapunov function V (x) and

there exist functions P

: R

→ R

1×m

and P

: R

→ N

such that

V (f (x) + G(x)u) = V (f(x)) + P

(x)u + u

(x)u, x ∈ R

, u ∈ R

Furth ermore, we assume that

∂

∂x



x=f(x)

> 0.

In this case, it can be shown using a Taylor series expansion about x =

f(x) that P

(x) = V

′

(f(x))G(x), P

(x) = G

(x)

∂

∂x



x=f(x)

G(x), and

NonlinearBook10pt November 20, 2007

834 CHAPTER 13

rank[P

(x) P

(x)] = rank P

(x), x ∈ R

. Next, note that the function

Γ(x)

△

= V (f(x) + G(x)u) −V (x) = V (f(x)) + P

(x)u + u

(x)u − V (x)

is a convex function since

∂

∂u

≥ 0, u ∈ R

, and h en ce, Γ(x) has a global

minimum. Now, setting

∂Γ

∂u

= 0 it follows that u = −

†

(x)P

(x). Hence,

inf

u∈R

Γ(x) = V (f(x)) −V (x) −

(x)P

†

(x)P

(x), which implies that

V (x) is a control Lyapunov f unction for G if and on ly if

V (f (x)) −V (x) −

(x)P

†

(x)P

(x) < 0, x ∈ R

, x 6= 0. (13.243)

In this case, a stabilizing feedback control law is given by φ(x) =

−

†

(x)P

(x).

13.16 Problems

Problem 13.1. Consider the dynamical system (13.1) with f(x) = Ax,

where A ∈ R

n×n

. Show that th e following statements are equivalent:

i) The zero solution x(k) ≡ 0 to (13.1) is Lyapunov stable.

ii) For every initial condition x

∈ R

, x(k) is bounded for all k ∈ Z

iii) If λ ∈ spec(A), then either |λ| < 1, or both |λ| = 1 and λ is semisimple.

iv) There exists α > 0 such that kA

k < α, k ∈ Z

Problem 13.2. Consider the dynamical system (13.1) with f(x) = Ax,

where A ∈ R

n×n

. Show that th e following statements are equivalent:

i) The zero solution x(k) ≡ 0 to (13.1) is globally asymptotically stable.

ii) For every initial condition x

∈ R

, lim

k→∞

x(k) = 0.

iii) If λ ∈ spec(A), then |λ| < 1.

iv) lim

k→∞

= 0.

Problem 13.3. Show that the zero solution x(k) ≡ 0 to (13.1) with

f(x) = Ax, where A ∈ R

n×n

, is asymptotically stable if and only if it is

geometrically stable.

Problem 13.4. Consider the dynamical system (13.1) with f(x) = Ax,

where A ∈ R

n×n

. Show that A is asymptotically stable if and only if there

exists a positive-deﬁnite matrix P ∈ R

n×n

that satisﬁes the discrete-time

Lyapunov equ ation

P = A

P A + R, (13.244)