Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере
Подождите немного. Документ загружается.

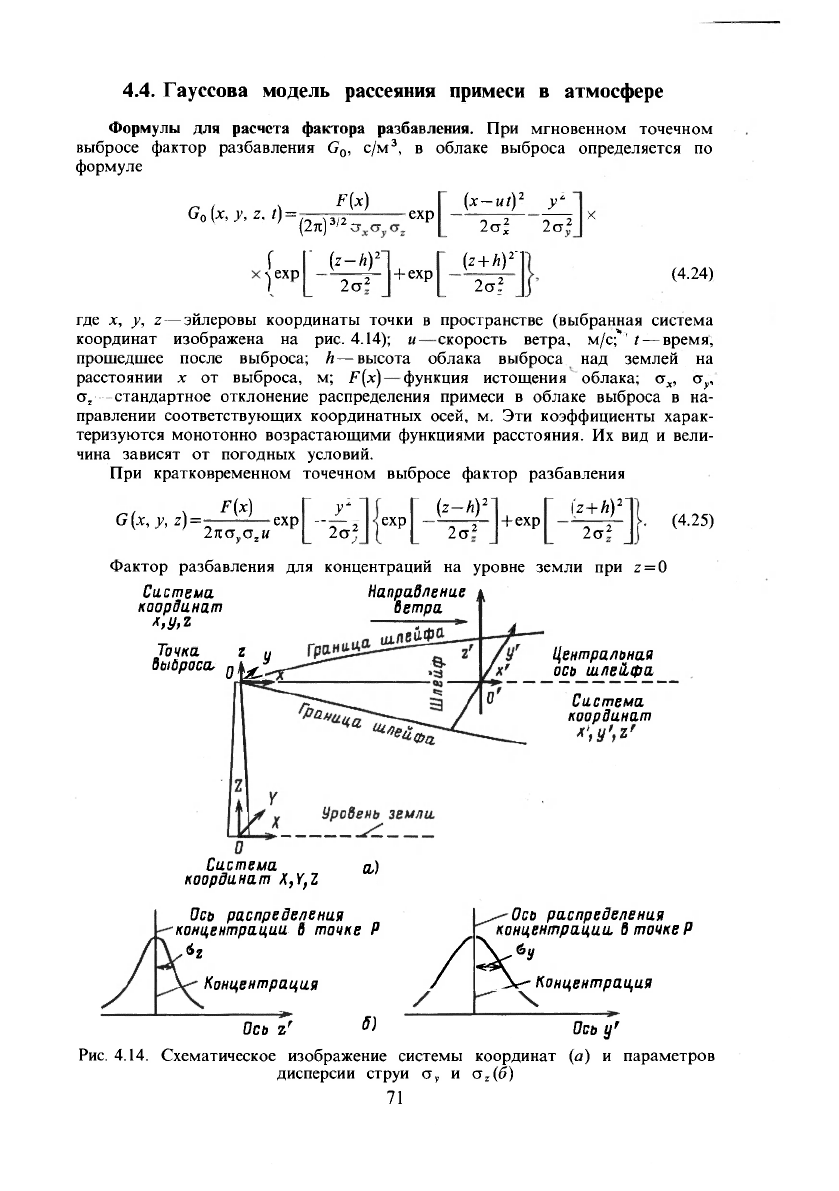
4.4. Гауссова модель рассеяния примеси в атмосфере
Формулы для расчета фактора разбавления. При мгновенном точечном
выбросе фактор разбавления G
0
, с/м
3
, в облаке выброса определяется по
формуле
G
0
(х, у, z, t) =
F(x)
(2к)
3/2.
f
• (z-/,)
2
l
•j
ex
P
2ст
2
-ехр
+ ехр
(x~ut)
2
2 ol
(z + hf
2 ст.
2
Zl
2ст
2
(4.24)
где х, у, z — эйлеровы координаты точки в пространстве (выбранная система
координат изображена на рис. 4.14);
и
— скорость ветра, м/с;
4
'
t
— время,
прошедшее после выброса;
h
— высота облака выброса над землей на
расстоянии х от выброса, м; F(x)—функция истощения облака; CT
I
, CT
J
,,
CT
z
стандартное отклонение распределения примеси в облаке выброса в на-
правлении соответствующих координатных осей, м. Эти коэффициенты харак-
теризуются монотонно возрастающими функциями расстояния. Их вид и вели-
чина зависят от погодных условий.
При кратковременном точечном выбросе фактор разбавления
G (х, у, z) =
F(x)
2па
у
о
г
и
ехр
Г
"2
Ct
2
ехр
(z-A)
2
2 CT
2
+ехр
z+hY
2 CT
2
(4.25)
Фактор разбавления для концентраций на уровне земли при z =
О
Система
координат
х,У, z
Точка г и
Выброса, и
3
Направление
Ветра
Центральная
ось шлейфа
Система
координат
Система &)
координат X
t
Y
l
Z
Ось распределения
концентрации В тачке P
*z
Концентрация
Ось Z
r
В)
Ось распределения
концентрации. В точке P
/V
y
/ Концентрация
Ось у'
Рис. 4.14. Схематическое изображение системы координат (а) и параметров
дисперсии струи CT
v
и CT
z
(б)
71

G(x, у, 0) =
F(x)
к
Ct
v
а. м
на оси струи при у = 0 и z = 0
F(x)
ехр
21
Zi
2
"
~2ст?
G(jc, 0, 0) = -
•ехр
/г
2
2ст?
Максимальное значение фактора разбавления на уровне земли
2F(X
max
) ст
г
G(x
max
, 0, 0) =
-
enuh
2
(4.26)
(4.27)
(4.28)
где е = 2,73 -основание натурального логарифма; /г— высота струи, м; X
max
—
расстояние от точки выброса, м, где реализуется максимум приземной
концентрации. Его можно получить, решая уравнение
0
z
{
Х
тах) —
h/\/2 ~ 0,707 h. (4.29)
При непрерывном выбросе средний за продолжительный период времени
(обычно 1 год) фактор разбавления определяется по формуле
G =
Л
(2к)
3/2,
f
• (z-hYl
<,ехр
2Ct
2
j
- J
— ехр
L
2ст
2
, Jj
(4.30)
где индексом j помечены величины, характерные для /-и категории устойчивости
атмосферы; M
j
— повторяемость /-Й категории за время выброса;
U
j
— средняя
в j-й погодной категории скорость ветра; г| — вытянутость розы ветров
в заданном направлении, определяемая формулой
Т|
=п/п
0
.
(4.31)
Здесь п — повторяемость направления вегра в заданном азимутальном
секторе при реальной розе ветров; п
0
— то же при круглой розе вет-
ров (при равновероятном направлении ветра). Строго говоря, пара-
метр т) должен стоять в формуле (4.30) под знаком суммы, так как
для разных погодных категорий розы ветров могут различаться. Одна-
ко в практических расчетах этим эффектом обычно пренебрегают. На
уровне земли
G=
2ц
(2к
13/2
V
w
J
p
J
] L-^-rr ехр
2ст
(4.32)
Среднегодовые факторы разбавления G (с/м
3
) на расстоянии от источника
100 км и более можно оценить по формуле
G =
г]Е(х)
2
пНТ
х
й.
(4.33)
Здесь Щ -среднее за год значение максимальной толщины слоя перемешива-
ния, м. Эта величина определяется формулой
HT
x
= max I J .'J
v
(z)dz/.J
y
(О)
(4.34)
где S^
v
(х, у, z)— объемная активность в воздухе в точке г над однородным
поверхностным источником. Величина Н"
ах
ограничивает диффузию в вер-
72

шкальном направлении. Обычно она совпадает с высотой до ближайшего,
достаточно мощного слоя инверсии температуры. Поэтому ее также довольно
просто определить по данным температурного зондирования атмосферы.
Диапазон ее изменения от 200 м зимой до 2000 м летом. На практике
HT
x
можно также определить, подставляя в (4.34) реально измеренные
вертикальные распределения концентрации естественной пыли или радона
и его дочерних продуктов в атмосфере. Ее численное значение определяется
также наиболее неустойчивой категорией в течение суток. Согласно гауссовой
модели диффузии
Гк
HT
x
= - ст™*« 1,25 ст™"*, (4.35)
где а'""
х
-предельное значение стандартного отклонения вертикального рас-
пределения примеси в облаке выброса. Его значения для разных категорий
устойчивости, взятые из [52], приведены в табл. 4.10.
Таблица 4.10. Значения верхней границы стT
x
для различных категорий
устойчивости
Категория
аТ", м
Категория
о"°
х
, M Категория
СТ™*, M
устойчивости устойчивости устойчивости
А 1600
С 640 E 220
В
920
D 400 F 100
Более подробно вопрос о физическом смысле и величине эквивалентной
толщины слоя перемешивания будет рассмотрен в разделе 4.12.
Определение коэффициентов дисперсии CT
v
и ст
г
. Существует несколько
способов оценки коэффициентов дисперсии а
у
и ст., входящих в формулы
предыдущего раздела. Они определяются в конечном счете путем сопоставления
результатов измерения концентрации примеси в воздухе от реальных источ-
ников с результатами расчетов по теоретическим формулам гауссовой модели
рассеяния на основе той или иной системы классификации погодных условий.
При этом для различных местностей и условий выброса получаются разные
результаты. Происходит накопление данных. Более поздние разработки обычно
учитывают предшествующий экспериментальный материал, который сохраня-
ется в международных и национальных информационных банках данных.
В настоящее время наиболее совершенны и чаще всего используются формулы
Смита- Хоскера [43, 60, 62, 63], согласно которым поперечную CT
J
, И вер-
тикальную ст. дисперсии при кратковременных выбросах, вертикальную
дисперсию ст. при непрерывных выбросах рассчитывают по следующим
формулам:
а
у
(.х)
= с
3
х/у/1 + 0,0001 л-; (4.36)
j/(-'o, приf(z *),
W
<ar-,1 з
(стГ'при f(z
0
,x)g(x)>ar
x
, j
где ст T
ax
—предельное значение ст. для данной категории устойчивости;
Z
0
— высота шероховатости подстилающей поверхности, см; х — расстоя-
ние от источника выбросов, м. Функции g(x) и /(z
0
, х) рассчитывают
по формулам:
73
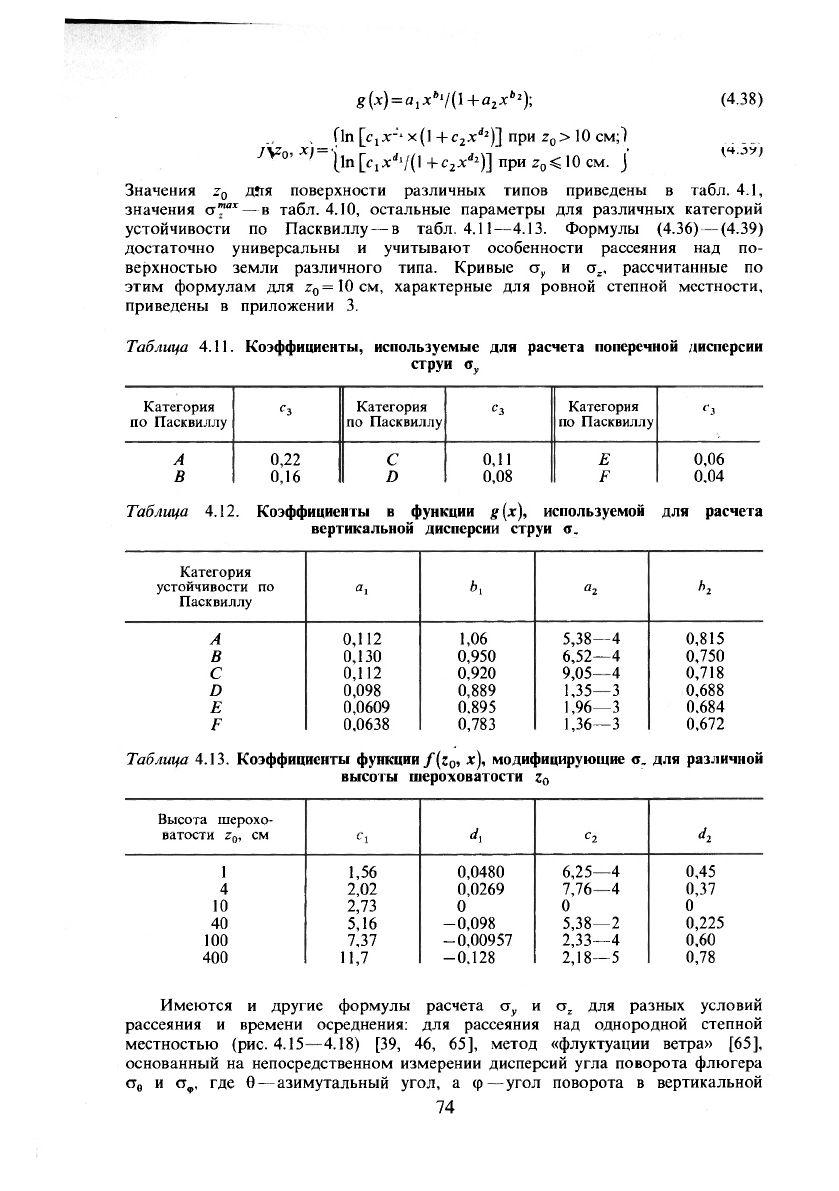
g(*) = a
1
x:
i
'
1
/(l +^
2
-*'
2
); (4.38)
fin [
Cl
x (1+ C
2
*'')] при Z
0
>10 см;)
JVo
' ' [In [с,*'»/(!+C
2
X'
1
)] при z
0
« 10 см. J '
Значения Z
0
дйя поверхности различных типов приведены в табл. 4.1,
значения а"
ах
- в табл. 4.10, остальные параметры для различных категорий
устойчивости по Пасквиллу — в табл. 4.11—4.13. Формулы (4.36) -(4.39)
достаточно универсальны и учитывают особенности рассеяния над по-
верхностью земли различного типа. Кривые а
у
и ст
г
, рассчитанные по
этим формулам для Z
0
=IOCM, характерные для ровной степной местности,
приведены в приложении 3.
Таблица 4.11. Коэффициенты, используемые для расчета поперечной дисперсии
струи G
y
Категория
C
3
Категория C
3
Категория
<'.1
по Пасквиллу по Пасквиллу
по Пасквиллу
А
0,22 С
0,11 E 0,06
В
0,16
D 0,08 F
0,04
Таблица 4.12. Коэффициенты в функции #(х), используемой для расчета
вертикальной дисперсии струи а.
Категория
устойчивости по
Пасквиллу
a
i
ь
1
а
2
A
2
А
0,112 1,06
5,38—4 0,815
В
0,130
0,950
6,52—4 0,750
С 0,112 0,920
9,05—4
0,718
D 0,098 0,889 1,35—3
0,688
E
0,0609 0,895 1,96—3
0,684
F
0,0638 0,783 1,36—3
0,672
Таблица 4.13. Коэффициенты функции /(г
0
, •*), модифицирующие а. для различной
высоты шероховатости Z
0
Высота шерохо-
ватости Z
0
, CM
d,
С
2
dг
1
1,56
0,0480
6,25—4
0,45
4 2,02 0,0269
7,76—4 0,37
10
2,73
0 0 0
40 5,16
-0,098 5,38—2 0,225
100 7,37 -0,00957
2,33—4 0,60
400 11,7 -0,128
2,18—5 0,78
Имеются и другие формулы расчета а
у
и CT
I
ДЛЯ разных условий
рассеяния и времени осреднения: для рассеяния над однородной степной
местностью (рис. 4.15—4.18) [39, 46, 65], метод «флуктуации ветра» [65],
основанный на непосредственном измерении дисперсий угла поворота флюгера
ст
е
и ст
ф
, где О -азимутальный угол, а «р- угол поворота в вертикальной
74
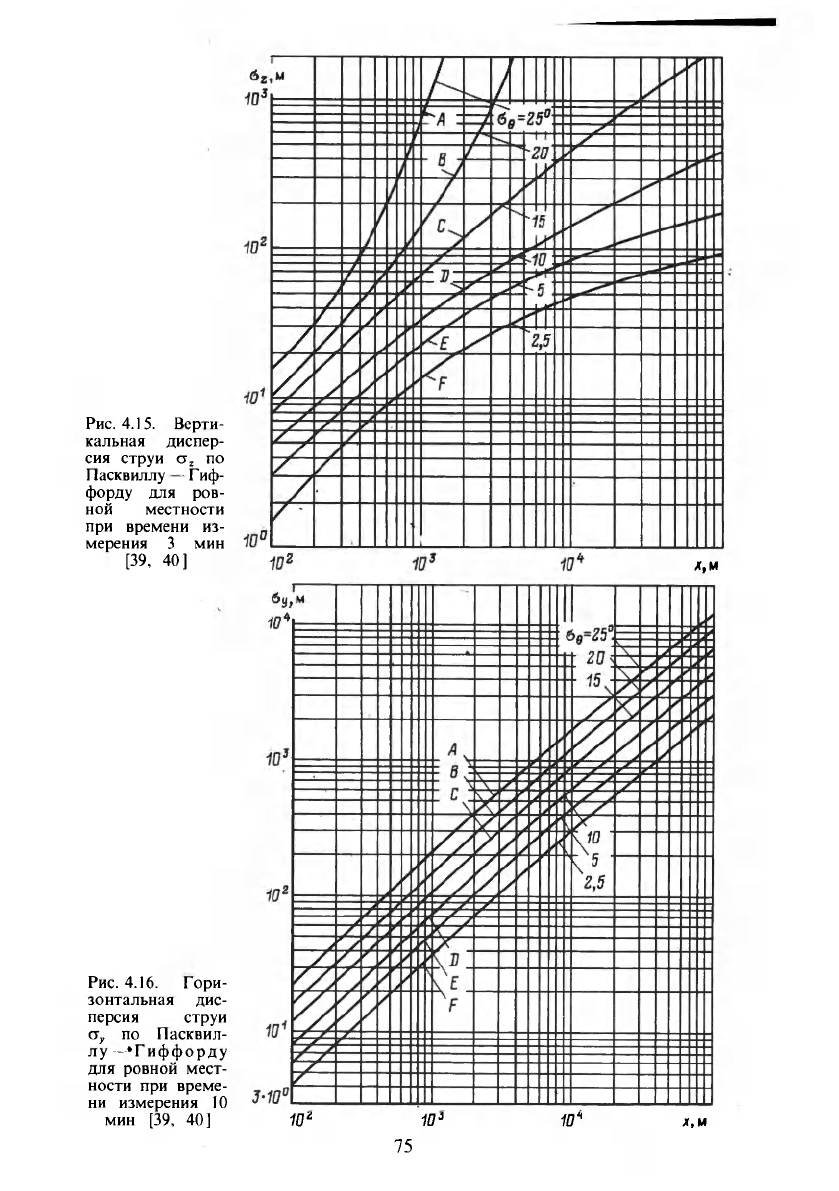
Рис. 4.15. Верти-
кальная диспер-
сия струи CJ
2
по
Пасквиллу — Гиф-
форду для ров-
ной местности
при времени из-
мерения 3 мин
[39, 40]
Рис. 4.16. Гори-
зонтальная дис-
персия струи
о
у
по Пасквил-
лу —«Гиффорду
для ровной мест-
ности при време-
ни измерения 10
мин [39, 40]
X
1
M
10
г
10
3
10" X, M
75
100
10
M
А _
и ^
/ / /
///>
////
УУ/
^^ J>-
ъъ* р.
/ ^
I IIIIIII
I IIIIIII
0,1 1
Расстояние по Ветру, км
10
Рис. 4.17. Вертикальная дисперсия
струи ст. по модифицированной мо-
дели Пасквилла — Гиффорда для
плоской пустыни при времени измере-
ния 1 ч [64]
Расстояние no lempy, км
Рис. 4.18. Горизонтальная дисперсия
струи CT
1
по модифицированной мо-
дели Пасквилла -Гиффорда для
плоской пустыни при времени измере-
ния 1 ч [64]
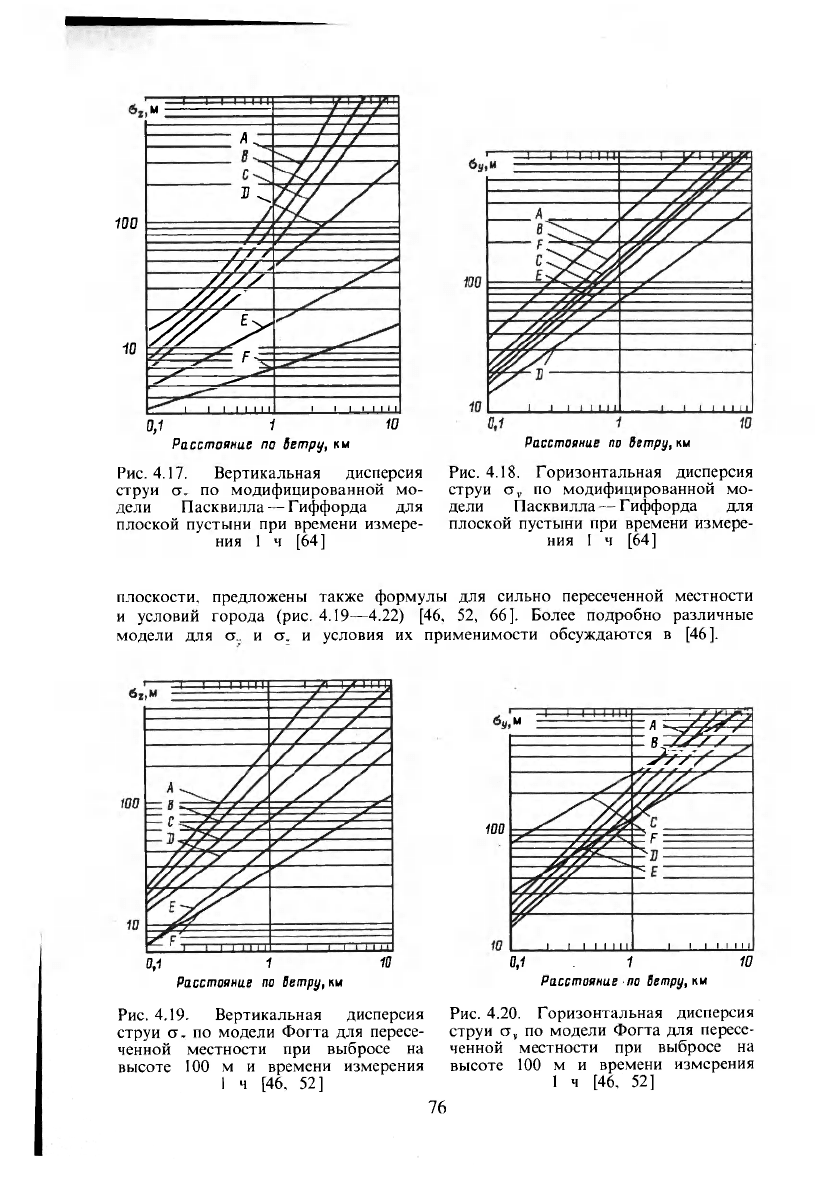
плоскости, предложены также формулы для сильно пересеченной местности
и условий города (рис. 4.19—4.22) [46, 52, 66]. Более подробно различные
модели для ст и ст. и условия их применимости обсуждаются в [46].
100
M
/I - уУУ/
в //у /
Jvs
F
I I Illlll
0,1 1 Ю
Расстояние по
Ветру, км
Рис. 4.19. Вертикальная дисперсия
струи ст. по модели Фогта для пересе-
ченной местности при выбросе на
высоте 100 м и времени измерения
I ч [46, 52]
0,1 1 1С
Расстояние по
Ветру,
км
Рис. 4.20. Горизонтальная дисперсия
струи ст, по модели Фогта для пересе-
ченной местности при выбросе на
высоте 100 м и времени измерения
1 ч [46, 52]
76
0,1 1
Расстояние по
Ветру,
км
0,1 1
Расстояние по
Ветру,
км
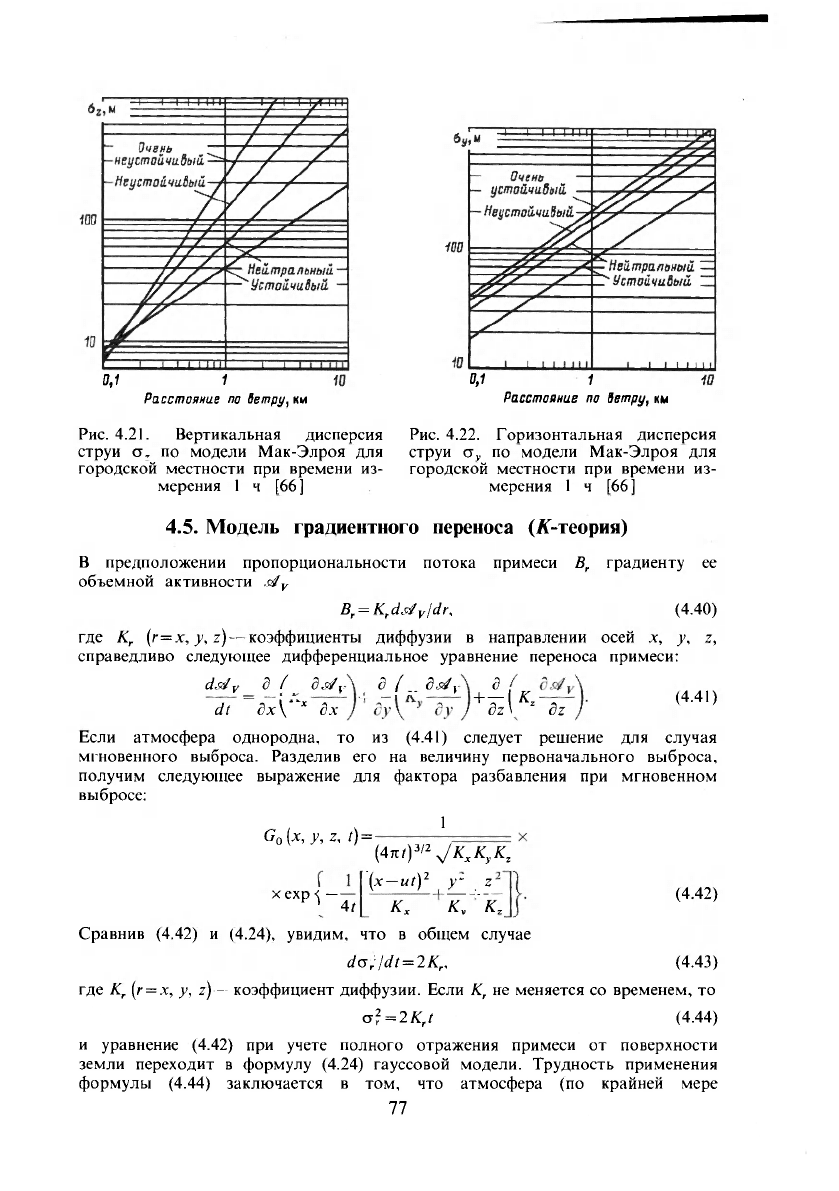
Рис. 4.21. Вертикальная дисперсия Рис. 4.22. Горизонтальная дисперсия
струи а, по модели Мак-Элроя для струи CT
j
. по модели Мак-Элроя для
городской местности при времени из- городской местности при времени из-
мерения 1 ч [66] мерения 1 ч [66]
4.5. Модель градиентного переноса (АГ-теория)
В предположении пропорциональности потока примеси B
r
градиенту ее
объемной активности stf
v
B
r
= K
r
dsi
v
\dr, (4.40)
где K
r
(г=х, у, г)— коэффициенты диффузии в направлении осей х, у, z,
справедливо следующее дифференциальное уравнение переноса примеси:
dsiy _ 8 / Sstf
i
dt ёх\
х
8х
, ^ f Sstf,
+
1\
к
-
Sz
(4.41)
Если атмосфера однородна, то из (4.41) следует решение для случая
мгновенного выброса. Разделив его на величину первоначального выброса,
получим следующее выражение для фактора разбавления при мгновенном
выбросе:
G
0
(х, у, z, t) =
1
(4тUy
1
JK
x
K
y
K
l
х ехр
<
> 41
\x-ut)
2
~ K
1
ZI
K
v
z
"к,
(4.42)
Сравнив (4.42) и (4.24), увидим, что в общем случае
da, /dt = 2K
r
, (4.43)
где K
r
(г = х, у, г)— коэффициент диффузии. Если K
r
не меняется со временем, то
а
2
= 2 K
r
t (4.44)
и уравнение (4.42) при учете полного отражения примеси от поверхности
земли переходит в формулу (4.24) гауссовой модели. Трудность применения
формулы (4.44) заключается в том, что атмосфера (по крайней мере
77

в вертикальном направлении) никогда не бывает однородной. И если
в гауссовой модели это игнорируется, формулу (4.24) рассматривают
как экстраполяционную, а значения ст
г
получают по результатам прямых
диффузионных экспериментов, то в рамках А-теории эту трудность обходят
теоретически. При этом формулируются различные упрощающие пред-
положения.
Обычно предполагают горизонтальную однородность коэффициентов A
v
,
K
y
и К,, стационарность по времени и пренебрегают диффузией в направлении
оси х по сравнению с переносом со средним ветром (т. е. полагают, что
K
x
= 0). При этом вместо (4.41) получают
, , SsJ
v
с д-р/у 8 SsJ
v
, ,,
^-ET'Ty^-bT^lf-
(4
'
45)
Его решение получают либо аналитически, задаваясь удобной аппроксимацией
зависимости скорости ветра и коэффициентов диффузии от высоты, либо
численно, моделируя процессы турбулентного переноса тепла и количества
движения в пограничном слое атмосферы. Подробно этот вопрос освещен
в [37, 49, 50].
Здесь мы приведем лишь одно из предложенных аналитических решений
уравнения (4.41), нашедших применение при расчетах рассеяния примеси на
стадии проектирования предприятий.
Предполагается степенная зависимость вертикального профиля коэф-
фициента диффузии К., а среднегодовая объемная активность sJ
v
.
Бк/м
3
, [67]
_ Qr
i
„ co,F,(х) /1\ ( А Д
где индекс j обозначает тип турбулентности атмосферы; Q - интенсивность
выброса, Бк/с; х— расстояние от точки выброса, м; и
0
- скорость ветра на
высоте 1 м, м/с; Fj(x) - функция истощения струи вследствие сухого оседания,
вымывания осадками и радиоактивного распада;
3 1
ос,=-
2
1
+ E-I-E
1
/г
1+Е+Е1
J
A(I-I-E-I-E
1
)'
1
+')/(1
+E
+ ei) (J
+£
_(_
gi
-e
+ El)/d
+ *
I-I-E
1
E-I-E
1
/i-эффективная высота выброса, учитывающая подъем струи, м; Г
гамма-функция; К- коэффициент вертикальной диффузии на высоте 1 м, м
2
/с;
Е, E
1
—параметры, зависящие от вертикального градиента температуры в ат-
мосфере; (Oj--повторяемость j-го типа турбулентности; г) вытянутость розы
ветров.
Параметр Е. характеризующий состояние атмосферы,
E= -0,2 Д Г, (4.47)
где Д T разность температур на высоте 1,4 и 13,4 м.
Параметр E
1
характеризует зависимость скорости ветра от высоты г:
M
= Mo
wz
'
1
", (4.48)
78
где T
1
= I м. Значения параметров к, и К в зависимости от значения параметра
е (т. е. от температурного градиента) для условий ровной степной местности
приведены в табл. 4.14.
Таблица 4.14. Зависимость устойчивости атмосферы от температурного градиента
и параметров вертикальной диффузии
Пара-
метр Конвекция
Нейтральная Инверсия
E
-0,2
-0,15 -0,1 -0,5 0 0,05
0,1
0,15 0,2
0,13 0,135
0,14
0,145 0,15 0,16 0,17
0,18 0,19
К, м
2
/с 0,09 0,08 0,07
0,06 0,05 0,026 0,015 0,009
0,005
Численные методы решения уравнения (4.45) достаточно сложны и требуют
применения ЭВМ. Они в наилучшей степени описывают процессы диффузии
в вертикальном направлении. Однако' имеются значительные трудности расчета
диффузии в горизонтальном направлении, особенно на больших расстояниях
от источника. Сложность математических моделей А'-теории является причиной
предпочтительного применения гауссовых моделей на расстояниях локального
масштаба. Иное дело расчеты в региональном и глобальном масштабах.
В таких случаях прибегают к лагранжевым моделям или к трехмерным
моделям А'-теории. которые должны учитывать следующие факторы: реальные
профили температуры воздуха, скорость и направление ветра на разных
высотах, изменение этих характеристик по мерс продвижения облака выброса,
тепловой подъем облака и опускание аэрозольных фракций за счет гравитаци-
онных сил, вымывание осадками и сухое оседание примеси на поверхность
земли.
Лагранжевы модели рассеяния, называемые также траекторными моделями,
предполагают: разбиение времени выброса- на короткие интервалы, выброс
в течение которых можно считать мгновенным, а процесс истечения примеси
дискретным, т. е. представлять его последовательными выбросами отдельных
клубов; вычисление траектории каждого клуба на основе реального поля
скорости ветра; расчет диффузионных характеристик отдельных клубов по
мерс их следования вдоль своих траекторий (с учетом изменения погодных
условий на разных участках траектории).
Существуют разновидности лагранжевых моделей, построенные на основе
как гауссовых моделей рассеяния, так и теории градиентного переноса.
Последние, как правило, отличаются большей точностью.
Трехмерные модели наиболее сложны, но зато обладают большей
точностью описания рассеяния примеси. Одна из возможных реализаций,
поясняющая суть этого метода, заключается в разбиении атмосферы на
отдельные объемы, малые настолько, чтобы внутри них все характеристики
можно было считать однородными (их в литературе иногда называют
боксами, а сами модели боксовыми). Для каждого такого элементарного
объема ищется решение уравнения (4.41) с учетом условий на его границах.
После процедуры «сшивания» граничных условий смежных объемов получается
целостная трехмерная картина рассеяния. При правильном определении
необходимых для таких расчетов полей метеорологических характеристик
можно надеяться на адекватность найденного распределения концентрации
примеси.
Лагранжевы и трехмерные региональные и глобальные модели рассея-
ния ввиду их сложности, как правило, не имеют аналитических реше-
79

ний. Единственно возможным путем их реализации является создание про-
грамм расчетов для ЭВМ. Более подробно эти методы изложены в
[51, 53, 55].
4.6. Метод «разделенной сигмы»
Метод разделенной сигмы объединяет лучшие стороны гауссовой модели
и теории градиентного переноса. Он позволяет обойти трудности А'-теории
в вопросе о рассеянии примеси в горизонтальном направлении и условность
гауссовой модели, которая построена в предположении вертикальной однород-
ности атмосферы. При этом полагают, что в поперечном к ветру направлении
примесь распределена по гауссиане с дисперсией <т,„ а вертикальное ее
распределение находят из решения уравнения диффузии, предлагаемой K-
теорией. Так, согласно [49] турбулентную диффузию примеси в случае
кратковременных выбросов описывают выражением
^y = Sexp(-^jjjJlKO
y
, (4.49)
где CT
y
(х)--дисперсия примеси в струе в перпендикулярном ветру направлении.
Для той или иной категории устойчивости его обычно полагают равным
соответствующим значениям гауссовой модели диффузии; S —двумерная
концентрация, Бк/м
2
, равная интегралу от объемной концентрации Бк/м
3
,
по поперечной направлению ветра горизонтальной оси у. Ее находят из
решения уравнения
SS SS S
u(z) W
Sx Sz Sz
SS
K
z
(z) —
Sz
= 0, (4.50)
где W -скорость гравитационного оседания примеси, u(z) и К{:) зависящие
от высоты скорость ветра и коэффициент верт икальной диффузии. Это уравнение
можно решать аналитически, моделируя закон изменения с высотой и (z) и K(z).
Например, аналог ично (4.46) при тех же предположениях справедлива формула
S=—7 . (4.51)
Смысл входящих в нес обозначений раскрыт в примечаниях к (4.46), однако
они относятся к конкретной категории устойчивости. Более точное решение
уравнений (4.50) можно получить, используя численный метод, предложенный
в [69]. Там же приведена программа для расчетов на ЭВМ.
4.7. Упрощенные методы расчета рассеяния примеси в атмосфере
Приближенная оценка среднегодового коэффициента метеорологического
разбавления G, с/м
3
, вблизи и на удалении до 10 км за зоной максимума
приземной концентрации может быть сделана по методу огибающей [69]:
2 n F(x)
G = ' (4.52
(2я) Jl
hux
где е = 2,73, а й- -средняя скорость ветра. Формула (4.52) дает максимальные
оценки в том смысле, что при любом законе изменения ст
2
и любой
80
