Гусев Н.Г., Беляев В.А. Радиоактивные выбросы в биосфере

Подождите немного. Документ загружается.

включая направление среднего ветра, за это время не меняются, а облако

выброса принимает форму струи.

Непрерывным называют продолжительный выброс, за время которого

направление ветра создает некоторое распределение по азимутальному углу

и можно говорить о розе ветров, а колебания интенсивности выброса при

этом не коррелируют с погодными условиями. Относительно редкие случаи,

когда осуществляются кратковременные повышенные выбросы, которые могут

давать значимый вклад в годовой интеграл концентрации в воздухе, не

следует включать в категорию непрерывных выбросов. Напротив, повышенные

кратковременные выбросы, которые не дают значимого вклада в годовой

интеграл концентрации, можно не выделять из категории непрерывных

выбросов, а при осреднении считать их случайным всплеском интенсивности

непрерывных выбросов.

Масштабы расстояний от источника выброса подразделяют на три класса:

1) в пределах нескольких десятков километров—локальный масштаб; 2) от

десятков до сотен километров — региональный масштаб (так называемый

мезомасштаб); 3) более тысячи километров — глобальный масштаб. Соответ-

ственно говорят о локальных, региональных и глобальных моделях рассеяния

примеси.

Математическое моделирование атмосферной диффузии развивается по

двум направлениям: на основе статистической теории, конечным резуль-

татом которой является гауссова модель распределения примеси в об-

лаке выброса, и путем решения дифференциальных уравнений переноса,

полученных в предположении пропорциональности потока примеси гради-

енту ее концентрации в воздухе (так называемой К-теории). Для обоих

направлений возможно

описание переноса примеси в эйлеровых и лагран-

жевых координатах.

При эйлеровом подходе рассеяние примеси рассматривают в системе

координат, связанной с местностью; при лагранжевом описании облако

выброса представляют в виде суперпозиции выброшенных клубов, а систему

отсчета последовательно связывают с отдельными клубами. Эйлерова система

хороша тем, что позволяет получать распределение концентрации примеси

на местности наиболее простым способом.

При лагранжевом описании необходимо знать траектории движения

отдельных клубов и рассматривать их продвижение, согласуясь с теку-

щими значениями скорости ветра и погодными условиями. В простей-

ших случаях, когда скорость ветра и погодные условия не меняются,

а все траектории можно считать совпадающими с направлением сред-

него ветра (что, например, вероятно для локальных масштабов расстоя-

ний при осреднении по времени), преимущества эйлерова подхода оче-

видны. При рассмотрении же переноса примеси на сотни и более кило-

метров требования неизменности погодных условий, постоянства скорости

ветра и траекторий отдельных клубов (даже при осреднении по времени)

становятся невыполнимыми. В этих случаях предпочтительны лагранжевы

модели рассеяния.

Из приведенного качественного описания процессов, участвующих в рас-

сеянии примеси в атмосфере, видно, какое большое число чрезвычайно

изменчивых и труднопредсказуемых факторов влияет на атмосферную диф-

фузию. Учесть их все в рамках одной математической модели не представляется

возможным. Обычно задачу упрощают, выделяя доминирующие в конкретных

условиях и игнорируя остальные факторы влияния. Местные условия от-

личаются большим разнообразием. Велико также различие возникающих

частных задач. Отсюда большое число предложенных моделей рассеяния.

Причем с ростом масштабов выбросов (особенно в аварийных условиях)

число влияющих на атмосферную диффузию факторов и разнообразие их

возможных комбинаций возрастает. Поэтому число предлагаемых моделей

рассеяния примеси в атмосфере будет возрастать и дальше. В ближайшее

время, вероятно, не удастся создать, и тем более декретировать, простую,

доступную всем универсальную методику расчета рассеяния примеси в ат-

мосфере. Задачу, Лю-видимому, можно решить, лишь применяя пакет различных

частных методов, число которых в конечном счете может быть значительным.

Подробный обзор существующих методов расчета рассеяния в атмосфере

можно найти в работах [35—37, 43, 46—51]. Здесь же мы изложим лишь

наиболее простые локальные модели рассеяния, рекомендуемые различными

международными и национальными организациями и нашедшими применение

при практических расчетах. Методы рассеяния в региональных и глобальных

масштабах изложены в [51—55].

Объемную активность радионуклидов в воздухе рассчитывают но сле-

дующим общим для всех моделей формулам:

для непрерывных и кратковременных выбросов

= QG, (4.1)

где Q интенсивность выброса, Бк/с; G фактор метеорологического раз-

бавления, с/м

;

для мгновенных выбросов

rfv(t) = Q

(t), (4.2.)

где Q

—интегральная величина мгновенного выброса, Бк; G

(е) — зависящий

от времени фактор метеорологического разбавления для мгновенно выброшен-

ного клуба примеси. В этом случае он имеет размерность м~

. Иногда [56]

используется обратная фактору разбавления величина, называемая коэффици-

ентом разбавления.

4.2. Классификация категорий устойчивости атмосферы

Наиболее широкое распространение получила схема классификации

погодных условий Пасквилла [38], согласно которой используется шесть

категорий устойчивости, распределенных по возрастанию степени устойчи-

вости атмосферы от А до F. Позднее для сильной устойчивости была

добавлена категория G. Однако из-за отсутствия достаточных данных по

рассеянию примеси при этих условиях, а следовательно, и достоверных

расчетных формул она практически не используется. Другие системы клас-

сификации погодных условий не всегда соответствуют категориям устой-

чивости Пасквилла, однако могут быть связаны с ними. В настоящее

время используются следующие системы классификаций категорий устой-

чивости атмосферы.^

1. Способ Пасквилла — Гиффорда. Он основан на измерении скорости

ветра на высоте 10 м и качественной оценке инсоляции в дневное время

и облачности в ночной период (за ночной принимается период, начинающийся

за час до захода солнца и заканчивающийся через час после его восхода).

Определение категории устойчивости производят согласно табл. 4.2. При

определениях о, и а, для категорий А, В и т. д. следует использовать

среднее значение А и В и т. д.

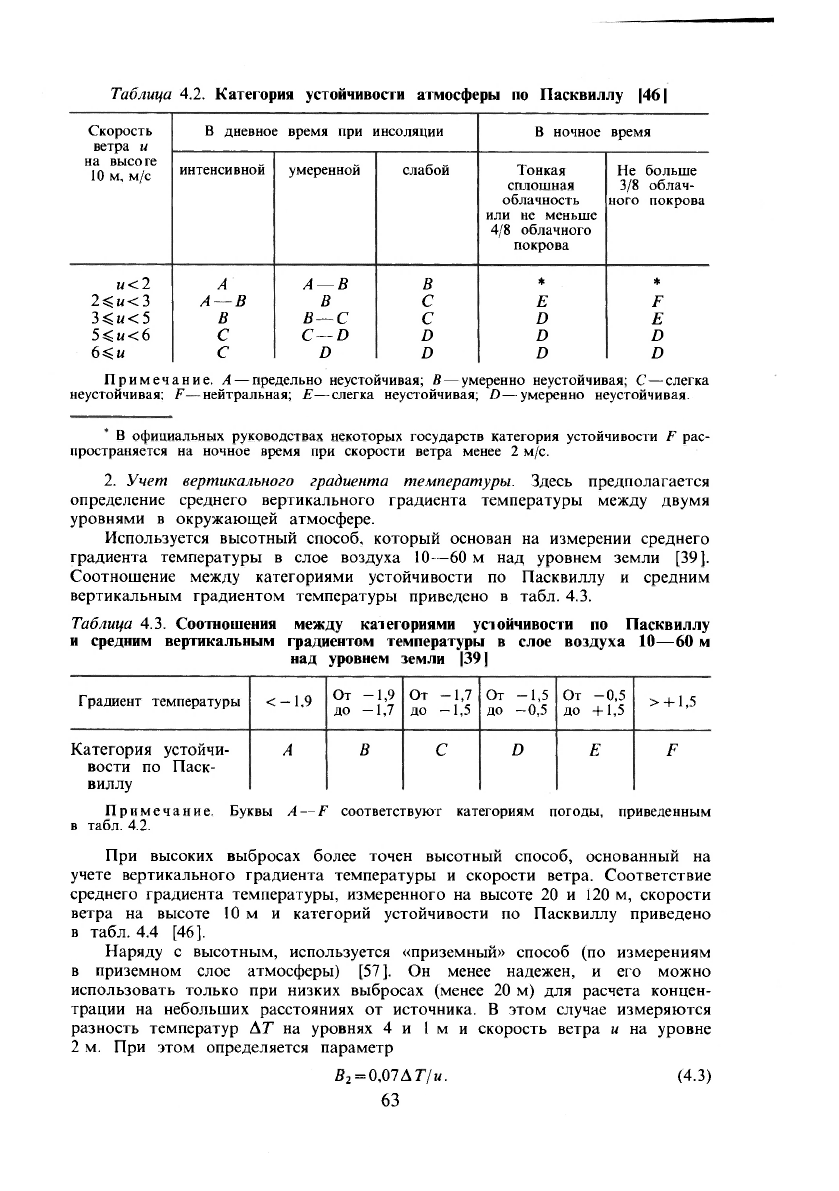
Таблица 4.2. Категория устойчивости атмосферы по Пасквиллу |46|

Скорость В дневное время при инсоляции

В ночное время

ветра и

на высоте

м, м/с

ветра и

на высоте

м, м/с

интенсивной

умеренной слабой

Тонкая Не больше

ветра и

на высоте

м, м/с

сплошная

облачность

или не меньше

4/8 облачного

покрова

3/8 облач-

ного покрова

и<2

А А — В В

2«;н<3 A--B В

С E F

3^м<5

В В С

С D E

5г£ы<6

С С D D D D

6 ^u с D

D D D

Примечание.

— предельно неустойчивая; В— умеренно неустойчивая; С—слегка

неустойчивая; F—нейтральная; E—слегка неустойчивая;

D —

умеренно неустойчивая.

В официальных руководствах некоторых государств категория устойчивости F рас-

пространяется на ночное время при скорости ветра менее 2 м/с.

2. Учет вертикального градиента температуры. Здесь предполагается

определение среднего вертикального градиента температуры между двумя

уровнями в окружающей атмосфере.

Используется высотный способ, который основан на измерении среднего

градиента температуры в слое воздуха 10—60 м над уровнем земли [39].

Соотношение между категориями устойчивости по Пасквиллу и средним

вертикальным градиентом температуры приведено в табл. 4.3.

Таблица 4.3. Соотношения между категориями устойчивости по Пасквиллу

и средним вертикальным градиентом температуры в слое воздуха 10—60 м

над уровнем земли |39 ]

Градиент температуры

<-1,9

От -1,9

до -1,7

От -1,7

до -1,5

От -1,5

до -0,5

От -0,5

до +1,5

> + 1,5

Категория устойчи-

вости по Паск-

виллу

А В

С D E F

Примечание. Буквы А — F соответствуют категориям погоды, приведенным

в табл. 4.2.

При высоких выбросах более точен высотный способ, основанный на

учете вертикального градиента температуры и скорости ветра. Соответствие

среднего градиента температуры, измеренного на высоте 20 и 120 м, скорости

ветра на высоте 10 м и категорий устойчивости по Пасквиллу приведено

в табл. 4.4 [46].

Наряду с высотным, используется «приземный» способ (по измерениям

в приземном слое атмосферы) [57]. Он менее надежен, и его можно

использовать только при низких выбросах (менее 20 м) для расчета концен-

трации на небольших расстояниях от источника. В этом случае измеряются

разность температур AT на уровнях 4 и 1 м и скорость ветра и на уровне

2 м. При этом определяется параметр

= 0,01 АТ/и.

(4.3)

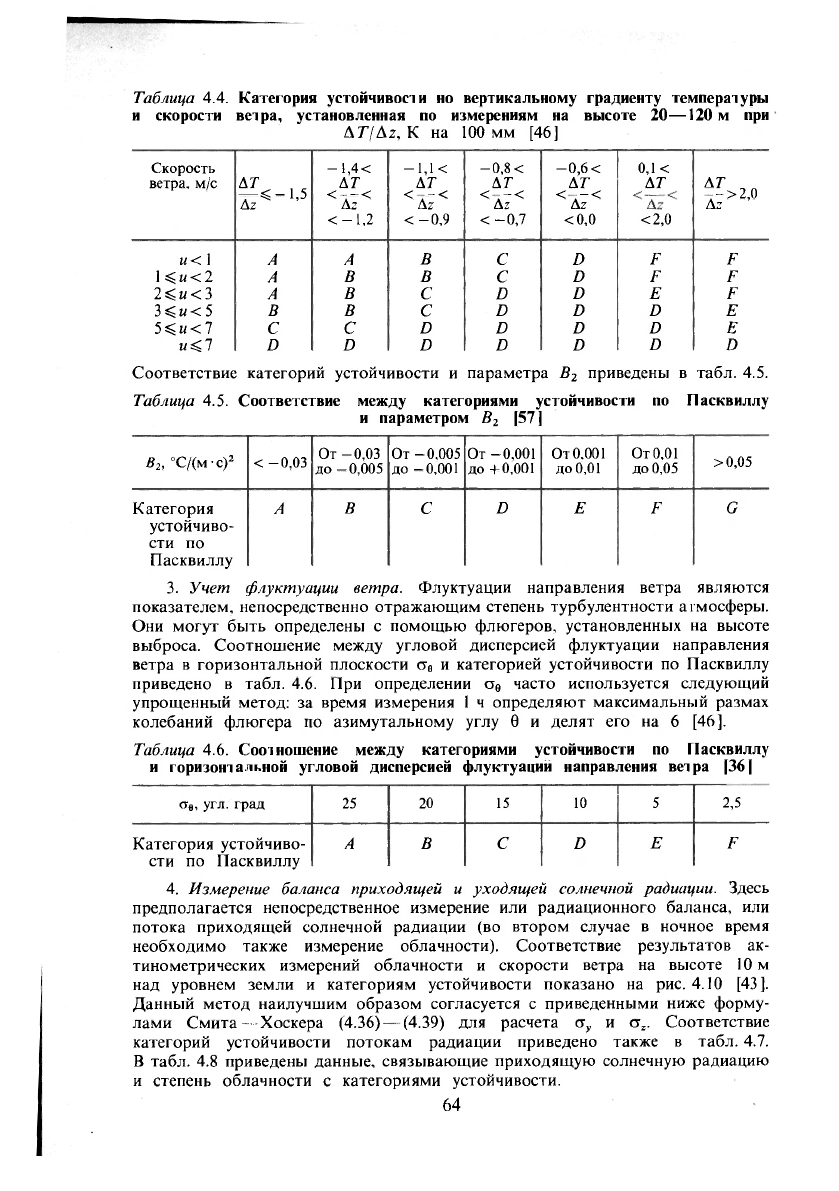
Таблица 4.4. Категория устойчивости но вертикальному градиенту температуры

и скорости ветра, установленная по измерениям на высоте 20—120 м при

Г/Az, К на 100 мм [46]

Скорость

ветра, м/с

A T

-<-1,5

—1,4<

д7

<-1,2

—1,1

«дГ

<-0,9

-0,8 <

Д^

<-0,7

-0,6<

Д?

<0,0

0,1

<2,0

д;

'°

и<

А А В С D F

sSM<2 А В В

D F F

2г£м<3

С D D

E F

Зг?м<5

В В

с D

D D E

5SSK<7 С с

D D D D E

U^l D D D D D

Соответствие категорий устойчивости и параметра B

приведены в габл. 4.5.

Таблица 4.5. Соответствие между категориями устойчивости по Пасквиллу

и параметром B

|57 ]

, °С/(м с)

<-0,03

От -0,03

до -0,005

От-0,005

до -0,001

От -0,001

до +0,001

От 0,001

до 0,01

От 0,01

до 0,05

>0,05

D E F G

Категория

устойчиво-

сти по

Пасквиллу

3. Учет флуктуации ветра. Флуктуации направления ветра являются

показателем, непосредственно отражающим степень турбулентности атмосферы.

Они могут быть определены с помощью флюгеров, установленных на высоте

выброса. Соотношение между угловой дисперсией флуктуации направления

ветра в горизонтальной плоскости G

и категорией устойчивости по Пасквиллу

приведено в табл. 4.6. При определении ст

часто используется следующий

упрощенный метод: за время измерения 1 ч определяют максимальный размах

колебаний флюгера по азимутальному углу О и делят его на 6 [46].

Таблица 4.6. Соотношение между категориями устойчивости по Пасквиллу

и горизонтальной угловой дисперсией флуктуации направления ветра |36|

, угл. град 25 20

15 10 5

2,5

Категория устойчиво-

сти по Пасквиллу

А В С D E

4. Измерение баланса приходящей и уходящей солнечной радиации. Здесь

предполагается непосредственное измерение или радиационного баланса, или

потока приходящей солнечной радиации (во втором случае в ночное время

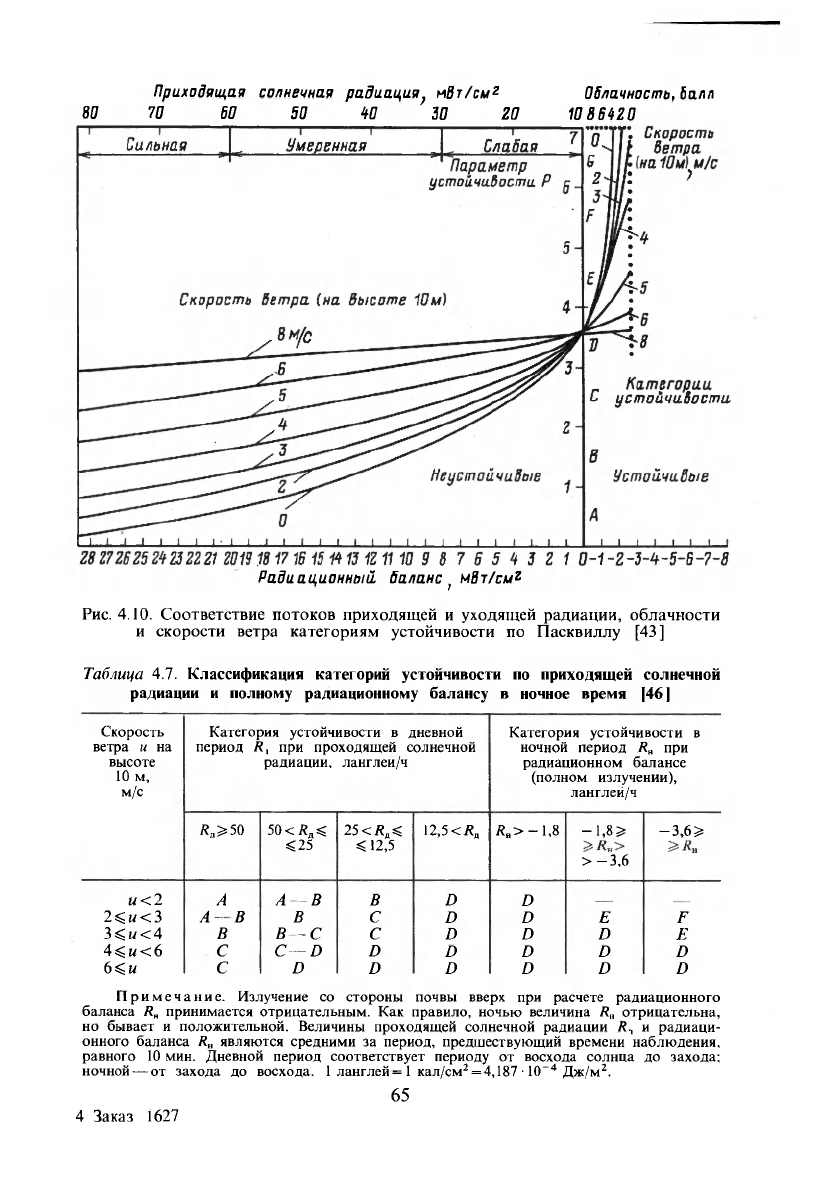
необходимо также измерение облачности). Соответствие результатов ак-

тинометрических измерений облачности и скорости ветра на высоте 10 м

над уровнем земли и категориям устойчивости показано на рис. 4.10 [43].

Данный метод наилучшим образом согласуется с приведенными ниже форму-

лами Смита- Хоскера (4.36)— (4.39) для расчета CT

и ст

. Соответствие

категорий устойчивости потокам радиации приведено также в табл. 4.7.

В табл. 4.8 приведены данные, связывающие приходящую солнечную радиацию

и степень облачности с категориями устойчивости.

ПрихоВящая солнечная радиация

;

мВт/см

Облачность, балл

80 70 ВО 50 40 30 ZO 10 8B4Z0

Радиационный, баланс

;

мйт/см

Рис. 4.10. Соответствие потоков приходящей и уходящей радиации, облачности

и скорости ветра категориям устойчивости по Пасквиллу [43]

Таблица 4.7. Классификация категорий устойчивости по приходящей солнечной

радиации и полному радиационному балансу в ночное время [461

Скорость

Категория устойчивости в дневной

Категория устойчивости в

ветра и на

период R

при проходящей солнечной

ночной период R,, при

высоте радиации,

ланглеи/ч радиационном балансе

10 м,

(полном излучении),

м/с ланглеи/ч

50 50 < Л

25 <Я„< 12,5 < Я„ Д„> —1,8

— 1,83=

-3,6>

<25 <12,5

>-3,6

и< 2 А A B В D

2<ы<3

A--B В

С D D E F

3<м<4 В

В—С С D D D

4<и<6 С C-D D

D D D D

6<И

D D D D

Примечание. Излучение со стороны почвы вверх при расчете радиационного

баланса R„ принимается отрицательным. Как правило, ночью величина R

отрицательна,

но бывает и положительной. Величины проходящей солнечной радиации R-, и радиаци-

онного баланса R

являются средними за период, предшествующий времени наблюдения,

равного 10 мин. Дневной период соответствует периоду от восхода солнца до захода;

ночной — от захода до восхода.

ланглей =

кал/см

4,187 •

Дж/м

4 Заказ 1627

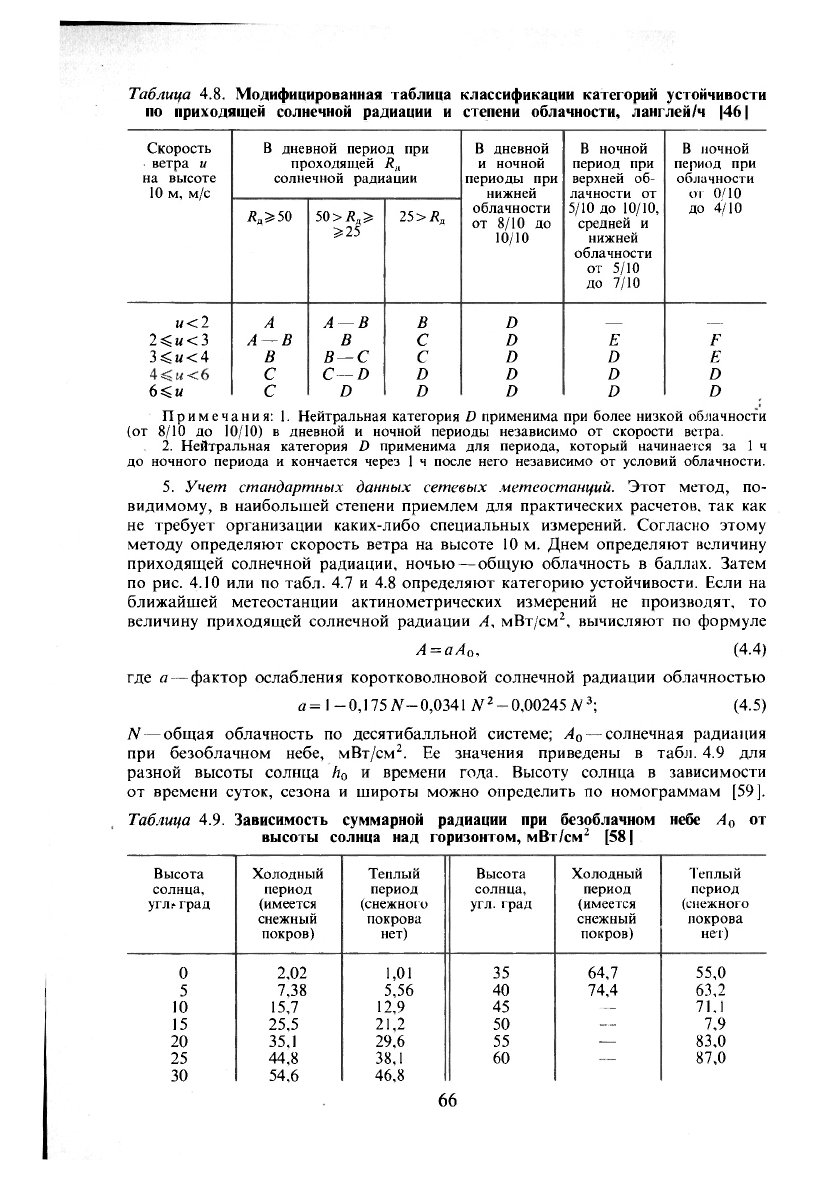
Таблица 4.8. Модифицированная таблица классификации категорий устойчивости

по приходящей солнечной радиации и степени облачности, ланглей/ч |46|

Скорость

ветра и

на высоте

10 м, м/с

В дневной период при

проходящей R

солнечной радиации

В дневной

и ночной

периоды при

нижней

облачности

от 8/10 до

10/10

В ночной

период при

верхней об-

лачности от

5/10 до 10/10,

средней и

нижней

облачности

от 5/10

до 7/10

В ночной

период при

облачности

от 0/10

до 4/10

Скорость

ветра и

на высоте

10 м, м/с

Я„> 50

>Я

>25

25 >R„

В дневной

и ночной

периоды при

нижней

облачности

от 8/10 до

10/10

В ночной

период при

верхней об-

лачности от

5/10 до 10/10,

средней и

нижней

облачности

от 5/10

до 7/10

В ночной

период при

облачности

от 0/10

до 4/10

и< 2 А А —В В D

2^и<3 А—В В

D E F

3^и<4 В

В—С с D D

С C-D

D D

6 =SM С

D D D

Примечания: 1. Нейтральная категория D применима при более низкой облачности

(от 8/10 до 10/10) в дневной и ночной периоды независимо от скорости ветра.

2. Нейтральная категория D применима для периода, который начинается за 1 ч

до ночного периода и кончается через 1 ч после него независимо от условий облачности.

5. Учет стандартных данных сетевых метеостанций. Этот метод, по-

видимому, в наибольшей степени приемлем для практических расчетов, так как

не требует организации каких-либо специальных измерений. Согласно этому

методу определяют скорость ветра на высоте 10 м. Днем определяют величину

приходящей солнечной радиации, ночью — общую облачность в баллах. Затем

по рис. 4.10 или по табл. 4.7 и 4.8 определяют категорию устойчивости. Если на

ближайшей метеостанции актинометрических измерений не производят, то

величину приходящей солнечной радиации А, мВт/см

, вычисляют по формуле

А = аА

, (4.4)

где а -фактор ослабления коротковолновой солнечной радиации облачностью

а=

—0,175 N— 0,0341 N

- 0,00245 N

-, (4.5)

N— общая облачность по десятибалльной системе; A

- солнечная радиация

при безоблачном небе, мВт/см

. Ее значения приведены в табл. 4.9 для

разной высоты солнца II

и времени года. Высоту солнца в зависимости

от времени суток, сезона и широты можно определить по номограммам [59].

Таблица 4.9. Зависимость суммарной радиации при безоблачном небе A

от

высоты солнца над горизонтом, мВт/см

[581

Высота

солнца,

угл? град

Холодный

период

(имеется

снежный

покров)

Теплый

период

(снежного

покрова

нет)

Высота

солнца,

утл. град

Холодный

период

(имеется

снежный

покров)

Теплый

период

(снежного

покрова

нет)

2,02 1,01 35 64,7

55,0

5 7,38

5,56 40

74,4 63,2

10 15,7 12,9 45

—

71,1

15 25,5

21,2

—

7,9

35,1 29,6 55

—

83,0

25 44,8 38,1

—

87,0

30 54,6

46,8

4.3. Условия выброса

Характер рассеяния выбросов, наряду с погодными факторами, зависит от

температуры, скорости истечения выбрасываемых газов и взаимодействия

ветрового потока с расположенными вблизи места выброса зданиями. Перегрев

по отношению к окружающему воздуху и скоростной напор выбрасываемых

газов вызывают подъем струи Л/г над точкой выброса, как это показано на

рис. 4.9. Влияние зданий сводится к искажению ветрового потока вблизи них

и к образованию зоны устойчивой циркуляции воздуха за зданием, так

называемой аэродинамической тени (рис. 4.11). При этом выбрасываемая

примесь может попадать в зону аэродинамической тени и быстро достигать

поверхности земли. В результате за зданием образуется объемный источник

примеси. Степень вовлечения выбрасываемой примеси в зону тени зависит от

места расположения устья трубы. Если источник выброса настолько высок, что

линии тока, проходящие через точку выброса, не попадают в зону смещения

потока (зона II на рис. 4.11), то образуется правильная струя и выбросы не будут

вовлечены в зону тени. При низких источниках, выбросы из которых попадают

в зону смещения потока (промежуточную зону), часть примеси окажется

вовлеченной в зону аэродинамической тени, а часть реализуется в форме

приподнятой струи. Выбросы из фонарей, расположенных на крыше зданий, из

окон и других проемов обычно полностью попадают в зону тени за зданием.

Выбросы из высоких труб. Высокими считают трубы, струя выбросов

из которых проходит выше зоны смещения потока (промежуточной зоны II

на рис. 4.11). В качестве грубого приближения высокими можно считать

трубы, устье которых выше двойной высоты наиболее высокого из ближайших

зданий. Для высоких груб траекторию струи рассчитывают по формуле

/г = /г

+Д/г —/г

—с, (4.6)

/—первичный поток; II—зона смещения (промежуточная зона); III—аэродинамическая

тень; IV—след; У граница зоны возмущения; 2—граница тени; S—граница следа;

4—8— профиль скорости ветра в продольном осевом сечении

где h

— геометрическая высота трубы от ее основания; Ah— динамический

(скоростной) и тепловой подъем струи над устьем; с—поправка на скос

струи при слабом ветре от влияния аэродинамической тени самой грубы.

Поправку на неровность местности h

вычисляют по следующим

формулам [60]:

{

0 при z

;

-Z

при z

+ 0,8(/; + A/i); ^ (4.7)

0,8(/г + Д/г) при z

>0,8(А + А/г),

где Z

— абсолютная высота основания трубы, м; z

— абсолютная высота

местности в точке детектирования, м.

Поправку с на скос струи от влияния аэродинамической тени трубы

вычисляют по формулам [61, 62]:

0 при W

^ 1,5м;

, (4.8)

3(1,5

—

/u)d при W

<1,5M,

где и - скорость ветра на уровне устья трубы, м/с; w— скорость истечения

выбросов, м/с; (/ диаметр устья трубы, м.

При расчете подъема струи

Д h

над устьем от скоростного напора

и плавучести выбросов необходимо учитывать, что он происходит постепенно,

образуя траекторию подъема струи до некоторой предельной высоты, которая

при неустойчивых атмосферных условиях определяется высотой до ближайшего

достаточно мощного слоя инверсии, а при устойчивых—предельной высотой

подъема, называемой эффективной высотой выброса или, если ниже этой

высоты имеется слой инверсии, высотой до его нижней границы.

Траектория подъема струи Ah для всех пригодных условий вычисляется

по следующей формуле [48]:

Ah= IMd^J" ^j

+^Ф

, (4.9)

где х — расстояние от основания трубы до точки детектирования, м; ir

и и

скорость ветра на высоте выброса и скорость истечения выброса соответ-

ственно, м/с; d - диаметр устья трубы, м;

Ф= (ATIT

)

Wod

/4 (4.10)

есть величина, пропорциональная потоку сил плавучести, м

/с

;

—абсолютная температура выброса, К; AT=T-T

— разность температур

выбрасываемого и атмосферного воздуха; g = 9,8 м/с

— ускорение свободного

падения. Зная тепловую мощность источника выброса Q

(Дж/с), величину

Ф можно рассчитать по формуле

Ф«1,04-10

. (4.11)

Первое слагаемое формулы (4.9) учитывает динамический подъем струи

в результате скоростного напора выброса [49], второе плавучий подъем

вследствие перегрева выбрасываемого воздуха [36]. В некоторых работах

выбросы таких предприятий, как АЭС, относят к категории холодных

и тепловой подъем для них рекомендуют не учитывать. Это, возможно,

справедливо летом. Зимой же пренебрегать тепловым подъемом нельзя.

Имеется несколько подходов для определения Ah

max

. В [37, 56] для

нейтральных условий предельный подъем струи

d( d А T\

ДЛ—= 3 2,5 + 3,3g-j— , (4.12)

S \

U f J

где U

скорость ветра на высоте флюгера, м/с. В [36, 61, 62] рекомендованы

следующие формулы:

для нейтральных условий

max

= 3—- +400—г; (4.13)

2 и и

для устойчивых условий при ветреной погоде

f WndV

/Ф\

1/3

Ali

max

= 1,55 "

1/6

(

——р ) +2,6 — ; (4.14)

V 2 JuJ \<«/

для устойчивых условий при штиле

Д/?

то

* =

5,1

,/4

318

, (4.15)

где и скорость ветра на высоте выброса, м/с;

S /эе\

— • (4.16)

\dz

Здесь ^--параметр устойчивости атмосферы; g— ускорение свободного падения,

/с; дв/дг— градиент потенциальной температуры (разница измеренного

и адиабатического градиента температуры), °С/м.

Для различных категорий можно принять:

8,7-IO

-4

для категории Е;

1,75 10 "

для категории F; ^ (4.17)

2,45 IO"

для категории G.

Выброс на уровне крыши зданий. При выбросе из фонарей, расположенных

на крыше, из окон и других проемов зданий примесь будет попадать в зону

аэродинамической тени с подветренной стороны здания, перемешиваться

в турбулентной струе, создаваемой потоком воздуха при обтекании здания,

и быстро достигать поверхности земли. Аналогичная картина будет наблюдать-

ся, если выбросы осуществляются из низкой трубы, но струя встречает

расположенное вблизи высокое здание. В результате формируется объемный

источник мощностью

= C

u, (4.18)

где и— скорость ветра, м/с; S

площадь сечения здания, перпендикулярного

направлению ветра, м

; C

—

коэффициент формы здания. Он определяется

при модельных экспериментах в аэродинамической трубе. Приближенно можно

принять C

= 0,5. Более подробно методы учета влияния зданий изложены

в [36, 56].

Выброс из низких труб. Низкими считаются трубы, высота которых

меньше высоты зоны смещения (промежуточной зоны Il на рис. 4.11),

образующейся в результате взаимодействия воздушного потока и близко

расположенного здания. Расчет для таких труб проводится по смешанной

модели, согласно которой доля примеси [I

—

к] выбрасывается как из высокой

трубы, и подъем струи рассчитывают по (4.6) --(4.17), а доля примеси,

0,2 0,4 O

B 0,8

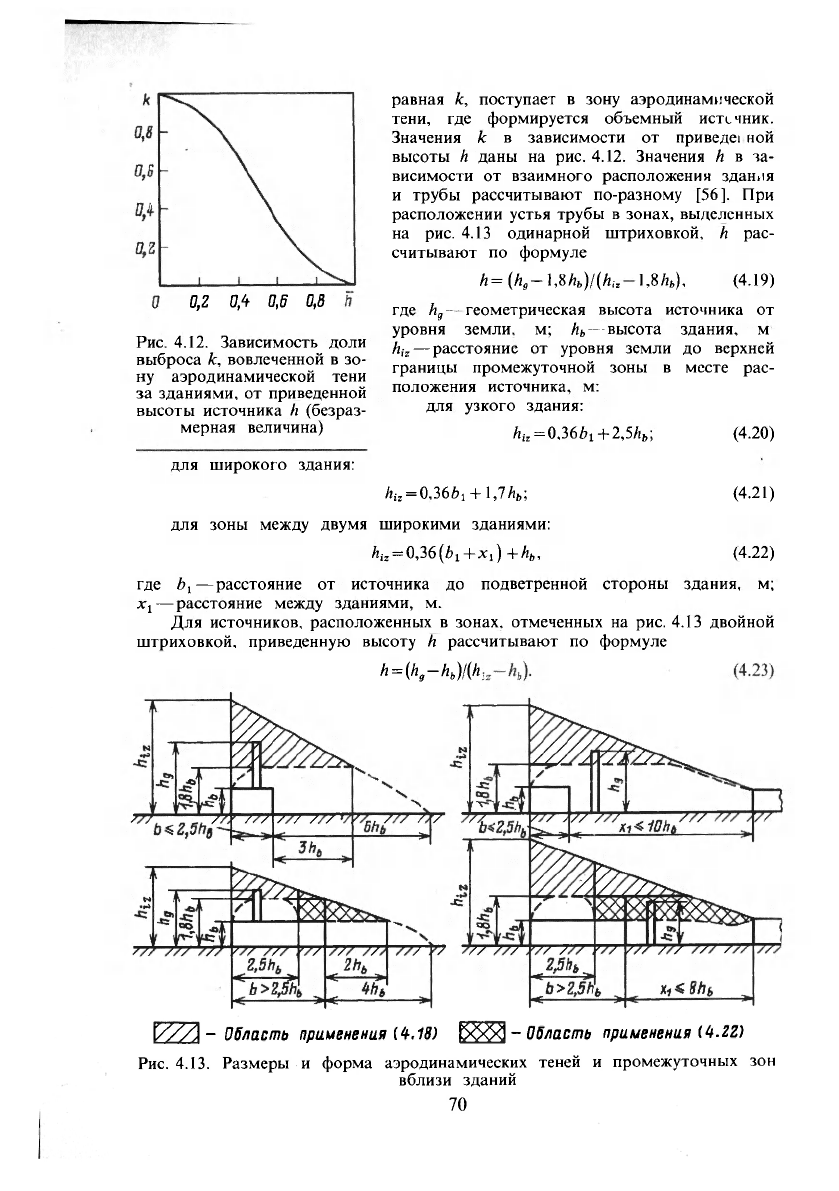
Рис. 4.12. Зависимость доли

выброса к, вовлеченной в зо-

ну аэродинамической тени

за зданиями, от приведенной

высоты источника /; (безраз-

мерная величина)

для широкого здания:

равная к, поступает в зону аэродинамической

тени, где формируется объемный истсчник.

Значения к в зависимости от приведе! ной

высоты h даны на рис. 4.12. Значения h в за-

висимости от взаимного расположения здания

и трубы рассчитывают по-разному [56]. При

расположении устья трубы в зонах, выделенных

на рис. 4.13 одинарной штриховкой, И рас-

считывают по формуле

h=(h,-\,U

)l(h

-l,Ut), (4.19)

где A

- геометрическая высота источника от

уровня земли, м; h

- высота здания, м

— расстояние от уровня земли до верхней

границы промежуточной зоны в месте рас-

положения источника, м:

для узкого здания:

1х

=0,366

+ 2,5А

;

= 0,366i + 1,7А

;

для зоны между двумя широкими зданиями:

1г

= 0,36

(ZJ

-I-Ar

) +h

(4.20)

(4.21)

(4.22)

где Ь

—расстояние от источника до подветренной стороны здания, м;

— расстояние между зданиями, м.

Для источников, расположенных в зонах, отмеченных на рис. 4.13 двойной

штриховкой, приведенную высоту И рассчитывают по формуле

h = (h

-h

)/(h

\//Л ~ Область применения (4.18) ^¾¾] - Область применения Cf.ZZ)

Рис. 4.13. Размеры и форма аэродинамических теней и промежуточных

вблизи зданий

зон