Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

42 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 1.17(a) Enhancement of

195

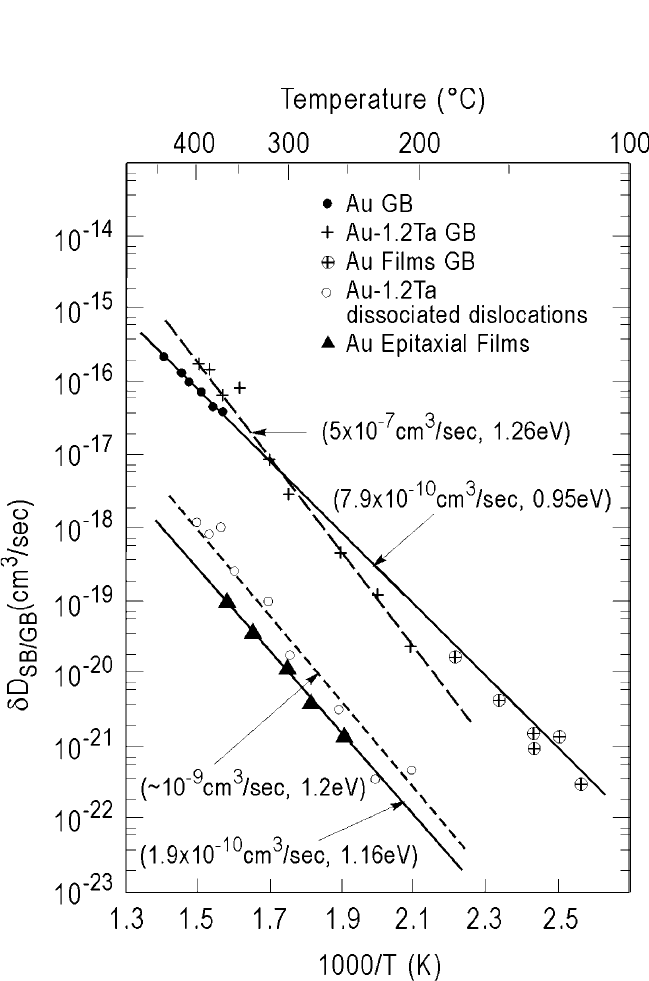
Au diffusion in the Au-1.2 at.% Ta alloy com-

pared with that in pure Au. The activation energies are 143 and 170 kJ/mol,

respectively. See also Fig. 1.4 for the mechanism.

[68]

Ch_01.qxd 11/30/04 8:36 AM Page 42

DIFFUSION IN BULK SOLIDS AND THIN FILMS, GUPTA 43

Figure 1.17(b) Grain boundary and sub-boundary diffusion of

195

Au tracer in

Au-1.2 at.% Ta alloy compared with that in pure Au in the boundaries of both kinds.

The activation energies are 121 and 92 kJ/mol for grain boundaries in Au-Ta alloy

and pure Au, respectively. The activation energy for sub-boundaries in both the

cases is 121 kJ/mol. (After Gupta and Rosenberg

[68, 89]

)

Ch_01.qxd 11/30/04 8:36 AM Page 43

1.5 General Characteristics of Grain

Boundary Diffusion

This section discusses general characteristics of grain boundary diffu-

sion and relates these characteristics to the lattice diffusion. It also touches

on some important properties of grain boundaries, as well as their

anisotropy and energy. Because this subject is vast, it cannot be covered

here in depth. A recent special issue of Interface Science

[69]

discusses the

latest developments in the field. Sutton and Balluffi’s book

[45]

deals in

depth with the microstructure, defects, and kinetic properties in the vari-

ous interfaces in crystalline solids. The handbooks by Kaur et al.

[70]

and

Volume 26 in the Landholt-Börnstein series

[71]

contain discussions and

data on various materials.

1.5.1 Anisotropy of Diffusion in Grain Boundaries

A grain boundary is essentially a two-dimensional transition region

between two crystals that have different orientations but the same perio-

dicity. The transition region leads to a very complex crystallographic

description of the grain boundary since 9 degrees of freedom or inde-

pendent variables are involved, which may be specified as 3 for the mis-

orientations, 3 for the choice of the GB plane, and 3 for the rigid-body

translation.

Figure 1.18(a) through (c) shows grain boundary diffusion of

119

radioactive tracer in polycrystalline Pb foils.

[72]

Contact auto-radiograms

were made on the entrance and exit sides of the foil after annealing at 90°C

for 100 hours, at which time the

119

Sn tracer emerged at the back surface.

To prevent cross talk between the two surfaces, the Pb foil thickness

(64 mm) was chosen to exceed 10 times the half-absorption thickness for

10 keV x-rays from

119

Sn with an absorption coefficient r  1000 cm

1

The auto-radiograms are compared with the grain boundary microstruc-

ture. Only a few grain boundaries, the high-angle ones, are seen in the

auto-radiograms through which the

119

Sn tracer diffused. The microstruc-

ture is in fact much finer, showing a variety of grain boundaries. Notably,

the twin boundaries are totally absent in the auto-radiograms. This is obvi-

ously due to variable diffusion kinetics in grain boundaries of differing

orientations. Grain boundary diffusion in polycrystalline Pb was subse-

quently measured by serial sectioning technique using

203

Pb radioactive

tracer.

[73]

In Fig. 1.19, GB self-diffusion coefficients (dD

/sec) using the

203

Pb radioactive tracer from Gupta and Kim

[73]

are shown in an Arrhenius

plot and are compared with earlier data of Stark and Upthegrove

[74]

as a

44 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_01.qxd 11/30/04 8:36 AM Page 44

DIFFUSION IN BULK SOLIDS AND THIN FILMS, GUPTA 45

function of orientation. The data in polycrystalline Pb are seen to go

through mostly the high-angle grain boundaries. These observations are

in accordance with the studies of Turnbull and Hoffman,

[75]

and Couling

and Smoluchowski,

[76]

on anisotropy of GB diffusion and its dependence

on the orientation angle q. In Ag tilt boundaries,

[100]

diffusion of

110

showed anisotropy of ∼15 for parallel and perpendicular directions at

Figure 1.19 Grain boundary diffusion in polycrystalline Pb and Pb bicrystals.

[73, 74]

Figure 1.18 Contact autoradiograms of the

119m

Sn tracer after diffusion in a Pb foil

at 90°C. (A) The plated or entrant surface, (B) the exit surface, and (C) the micro-

structure. The field of view is 1.25 cm in all cases. Note the similarity in the grain

structure. (After Gupta and Campbell

[72]

)

Ch_01.qxd 11/30/04 8:36 AM Page 45

450°C. The anisotropy progressively declined for orientations near

Σ  13 (q  23 degrees), Σ  17 (q  28 degrees), Σ  5 (q  36 degrees),

and so forth. The anisotropy of diffusion within the GB plane can be

understood on the basis of the distribution and nature of GB dislocations,

which predict channels of free volume parallel to the tilt axis in large-

angle boundaries. The diffusion coefficients and penetration distance

along GBs are also expected to show discontinuities and cusps as a func-

tion of misorientation angle similar to the GB energies because the con-

tributing factor in both cases should be the coincident lattice sites and the

GB dislocations. The activation energy for GB diffusion, however,

appears to remain independent of the orientation and Q

Q

≈ 0.4

(±20%), as in the case of GB diffusion in Pb, where Q

 42 kJ/mol (0.44

eV) and Q

 106 kJ/mol (1.1 eV). Thus, the anisotropy and orientation

dependence of GB diffusion may be largely due to changes in the pre-

exponential term D

1.5.2 Diffusion Mechanisms in Grain Boundaries

This section briefly examines the structure of grain boundaries and

the associated defects to explain possible diffusion mechanisms in

grain boundaries. This subject is exhaustive and complex, and only a

qualitative description of the gross features of grain boundaries is pos-

sible here. Sutton and Balluffi

[45]

and Balluffi

[77]

discuss this subject in

depth. Grain boundaries have been shown to be a world in themselves,

with a potpourri of defects such as the vacancies, interstitials, and dis-

locations. Because a grain boundary is a transition structure between

two crystals, perfectly two-dimensional periodic arrays would only

develop at some discrete choices of GB variables. To account for any

arbitrary choice of orientations and translations, incorporation of line

defects is required.

Extensive grain boundary structure studies have been conducted

over the past several decades

[78, 79]

using techniques such as high-reso-

lution transmission microscopy and computer stimulation, from which

the following broad features of grain boundaries have emerged (see

Chapter 3). First, the grain boundary is found to be relatively narrow,

on the order of a few atomic distances only. Second, the atomic pack-

ing in the GB core is only slightly less dense than in the perfect crys-

tal. Although the core structure has finite excess volume, much of it

may be considered to be relaxed by the development of a variety of

atomic groupings and localized configurations. Some boundaries have

short wavelength periodicity running parallel to the coincident site

46 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_01.qxd 11/30/04 8:36 AM Page 46

DIFFUSION IN BULK SOLIDS AND THIN FILMS, GUPTA 47

lattice (CSL) and are generally of low energy compared to the bound-

aries with long periodicity; the former may be termed special bound-

aries. In the case of arbitrary misorientation between two crystals, the

grain boundary minimizes its energy by preserving patches of the spe-

cial low-energy-ordered boundary and introducing therein arrays of

intrinsic grain boundary dislocations. It is also possible to have partial

grain boundary dislocations and extrinsic grain boundary dislocations

in the grain boundaries.

There is indirect experimental evidence from which a localized

structure of vacancies may be inferred with little relaxation of the

neighboring atoms. First, there was the measurement of pressure

dependence of the GB self-diffusivities in Ag by Martin et al.,

[80]

which

resulted in a value of ∆V

V

 1.1, where V

is the activation volume

for GB self-diffusion defined analogous to Eq. (34) and V

is the atomic

volume. The value of ∆V

is of the order of atomic volume in grain

boundaries and compares very favorably to its counterpart in the lattice

(Table 1.2).

Second, the isotope effect measurement for self-diffusion in Ag grain

boundaries by Robinson and Peterson

[81]

has also resulted in a relatively

large value of ∆E

∼ 0.46, which is temperature-insensitive. The corre-

sponding value of the isotope effect for self-diffusion in lattice is 0.65 

∆E

 0.71; the variation is due to some temperature dependence (Table

1.2). If the mobile defects responsible for GB diffusion were partially dis-

sociated or highly relaxed vacancies, a correlated movement of a number

of atoms would be required for diffusion to occur. Therefore, only a small

isotope effect value would have been observed. The experimental data,

however, neither support nor rule out contribution of interstitial atoms to

grain boundary diffusion. Atomistic computer modeling of point defects

in grain boundaries, using various techniques such as kinetic Monte Carlo

and molecular dynamics, have shown that vacancies as well as interstitial

atoms are stable, depending on the misorientation of the boundary and the

host crystal lattice.

[82]

Both defects have similar attractive binding ener-

gies in the grain boundaries, are mobile, and account for diffusion under

certain conditions. Suzuki and Mishin

[82]

have studied the role of intersti-

tial atoms and vacancies in Cu grain boundaries in detail. They noted

that diffusion in the Σ  5(310) [001], commonly considered a typical

grain boundary, was dominated by the interstitial atoms, whereas other

boundaries, the Σ  5(210)[001], Σ  9(12

–

2)[011], Σ  11(31

–

1)[011],

Σ 7(23

–

1)[111], and Σ  13(34

–

1)[111], were dominated by vacancies. In

any event, grain boundary diffusion is many orders of magnitude faster

than in the lattice. In Sec. 1.5.3, a thermodynamic model is discussed to

explain this difference.

Ch_01.qxd 11/30/04 8:36 AM Page 47

1.5.3 Interrelationship Among Grain Boundary,

Lattice Diffusion, and Energy

As mentioned in Sec. 1.5.2,

[45]

grain boundaries have lower density of

the interfacial material, which implies additional energy associated with

the microstructure and consequently an easier atomic diffusion. In the

past four decades, several investigators, notably Borisov et al.,

[83]

have

attempted to correlate the energy of the interfaces with diffusion kinetics.

The terms grain boundary and interface are used interchangeably

because this discussion will also include interfaces in several multiphase

alloys. The basic postulate in obtaining interface energy (g

) from self-

diffusion data is that it is the difference between the Gibbs free energies

(∆G

and ∆G

) for vacancy diffusion in the lattice and the interface, as

shown schematically in Fig. 1.20. The difference is positive because dif-

fusion in interfaces is many orders of magnitude faster than that in the

adjoining lattice. Hence the interface energy can be written as:





(∆G

 ∆G

) (66)

The factor of 1/2 enters because the interface energy is shared

between the two adjoining crystals. The Arrhenius nature of the coeffi-

cient, D, is given by Eqs. (27) through (29). The subscripts l and i denote

the lattice and grain boundary diffusion processes, respectively. The dif-

ference between the free energies, ∆G

and ∆G

, is then expressed as:

(Jmol) 



(∆G



 ∆G

) 



RT {n (D

D



)} (67)

(Jm

)  r{(Q



 Q

)  RT n(D

D



)}, (68)

where D

and D

/sec) are the pre-exponential terms for lattice and

interface diffusion, respectively; the conversion parameter r  12a

with a the mean distance between atoms at the interface, to the first

approximation, equal to one lattice parameter; and N

is Avogadro’s num-

ber. Q

and Q

, and R, the gas constant within the brackets, are to be taken

in J/mol.

To test that grain boundary energies computed from diffusion data are

indeed meaningful, diffusion parameters and the resulting interface ener-

gies obtained from Eq. (68) for several pure metals are compared in Table 1.4

with the direct measurements of interface energies using nondiffusion

48 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_01.qxd 11/30/04 8:36 AM Page 48

DIFFUSION IN BULK SOLIDS AND THIN FILMS, GUPTA 49

techniques such as the zero creep and transmission electron microscopy

(TEM). Figure 1.21 shows a plot of the two kinds of interfacial energies.

Despite the semi-empirical nature of the basic postulate in Eqs. (66)

through (68), the two kinds of interfacial energies agree well, within a few

percent.

Because the diffusion processes, in general, are related to the absolute

melting temperature of the host,

[84]

the grain boundary energies should also

be thus related. Physically, such a dependence stems from the cohesive

energy of the solid that controls the atomic motions as well as the energy

of the grain boundary itself. Chapter 2 discusses this topic in detail. The

Figure 1.20 Schematic representation of grain boundary energy (g

) and free ener-

gies for diffusion in lattice and grain boundaries. Note the decrease in g

by ∆G

upon addition of a solute. (After Borisov et al.

[83]

)

Ch_01.qxd 11/30/04 8:36 AM Page 49

50 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Table 1.4. Diffusion in Lattice (Q

, D

), GB (Q

, dD

), and GB Energies (g

)

in Pure Metals

Lattice Grain Boundary

Host Q

D°

DD°

Energy(g

) Reference

(Tracer) (kJ/mol) (10

4

/s) (kJ/mol) (10

16

/s) (mJ/m

)

Au(

195

Au) 169.6 0.04 84.8 3.1 396-0.016T a

Au* ... ... ... ... 400(1173K) b(*)

Ag(

110

Ag) 169.6 0.04 77.1 0.13 382(1173K) c

Ag(

110

Ag) 169.6 0.04 74.4 0.31 392(1173K) d

Ag* ... ... ... ... 400(1173K) e(*)

Cu(

110

Ag) 199.4 0.16 75.2 23 776-0.123T f

Cu(

Cu) 196.8 0.1 84.75 11.6 783-0.134T g

Cu(

Cu) 199.4 0.16 91.5 29 692-0.0054T h

Cu* ... ... ... ... 590(1123K) b

Ni(

Ni) 277.5 0.92 170.5 222 1126-0.214T i(*)

Ni* 277.5 0.92 ... ... 1373-0.4T j(*)

Pb(

203

Pb) 100 0.16 44.3 61 193-0.004T k

Pb(

119

Sn) 99.4 0.41 39.5 73 206-0.03T l

Pb* ... ... ... ... 200(588) m(*)

* Actual measurements

a. D. Gupta, Metall. Trans., 8A:1432 (1977)

b. J. E. Hilliard, M. Cohen, and B. L. Averbach, Acta Metall., 8:26 (1959)

c. D. Turnbull and R. E. Hoffman, Acta Metall., 2:419 (1954)

d. J. T. Robinson and N. L. Peterson, Acta Metall., 21:1181 (1973)

e. A. P. Greenough and R. King, J. Inst. Metall., 79:415 (1951

f. G. Barreau, G. Brunel, G. Cizeron, and P. Lacombe, Mem. Sci. Rev. Metall., 68:357 (1971)

g. T. Surholt and C. Herzig, Acta Mater., 45:3817 (1997)

h. D. Gupta, Defect Diffusion Forum, 156:43 (1998)

i. W. Lange, A. Hassner, and G. Mischer, Phys. Status Solidi, 5:63 (1964)

j. L. E. Murr, R. J. Horilev, and W. N. Lin, Philos. Mag., 22:52 (1970)

k. D. Gupta and K. K. Kim, J. Appl. Phys., 51:2066 (1980)

l. K. K. Kim, D. Gupta, and P. S. Ho, J. Appl. Phys., 53:3620 (1982)

m. K. T. Aust and B. Chalmers, Proc. Royal Soc., A204:359 (1950)

activation energies for diffusion in the lattice and grain boundaries, respec-

tively, are related to the absolute melting temperature (T

) of the host

[51]

as:

 142 T

Jmol (±20%) and Q

 71 T

Jmole (±20). (69)

Consequently, Eq. (68) can be rewritten as:





(mJm

), (70)

Ch_01.qxd 11/30/04 8:36 AM Page 50

DIFFUSION IN BULK SOLIDS AND THIN FILMS, GUPTA 51

neglecting contributions of the log of pre-exponential terms in the dif-

fusion coefficients. As seen in Table 1.4, the temperature coefficient of

in pure metals is small and negative, implying a positive entropy

≈ 0.25 mJ/m

°C for grain boundaries. The value of g

≈ 0.24T

Figure 1.21 Comparison of diffusion-related grain boundary energies in pure met-

als with those measured directly.

Ch_01.qxd 11/30/04 8:36 AM Page 51