Griffiths R.B. Consistent Quantum Theory

Подождите немного. Документ загружается.

224 Quantum reasoning

questions one is interested in, for in the end one will always get precisely the same

answer to any particular question.

16.4 Interpretation of multiple frameworks

The example of Sec. 16.2 illustrates a situation which arises rather often in rea-

soning about quantum systems. The initial data D can be used in various different

frameworks F

, F

,... , to yield different conclusions C

, C

,.... The question

then arises as to the relationship among these different conclusions. In particular,

can one say that they all apply simultaneously to the same physical system? Gen-

erally the conclusions are expressed in terms of probabilities that are greater than

0 and less than 1, and thus involve some uncertainty. But sometimes, and we de-

liberately focused on this situation in the example in Sec. 16.2, one concludes that

an event (or history) has probability 1, in which case it is natural to interpret this

as meaning that the event actually occurs, or is a “true” consequence of the initial

data. Similarly, probability 0 can be interpreted to mean that the event does not

occur, or is “false”.

If two or more frameworks are compatible, there is nothing problematical in

supposing that the corresponding conclusions apply simultaneously to the same

physical system. The reason is that compatibility implies the existence of a com-

mon reﬁnement, a frameworkG which contains the projectors necessary to describe

the initial data and all of the conclusions. The consistency of quantum reasoning,

Sec. 16.3, means that the conclusions C

will be identical in F

and in G. Conse-

quently one can think of F

, F

,... as representing alternative “views” or “per-

spectives” of the same physical system, much as one can view an object, such as a

teacup, from various different angles. Certain details are visible from one perspec-

tive and others from a different perspective, but there is no problem in supposing

that they all form part of a single correct description, or that they are all simultane-

ously true, for the object in question.

In the example considered in Sec. 16.2, F

could be the framework based on

(16.2), which allows one to describe the position of the particle at t = 1, but not

for any other t > 0, and F

the one based on (16.6), which provides a description

of the position of the particle at t = 2, but not at t = 1. Their common reﬁnement

provides a description of the position of the particle at t = 1 and t = 2, and F

and

can be thought of as supplying complementary parts of this description.

Conceptual difﬁculties arise, however, when two or more frameworks are incom-

patible. Again with reference to the example in Sec. 16.2, let F

be the framework

based on (16.5). It is incompatible with F

, because X

∗c

in (16.2) and X

∗a

(16.5) do not commute with each other, since the projectors [1c] and [1¯a]att = 1

do not commute. From the initial data one can conclude using F

that the particle

16.4 Interpretation of multiple frameworks 225

possesses the property [1c]att = 1 with probability 1. Using F

and the same ini-

tial data, one concludes that the particle has the property [1¯a]att = 1, again with

probability 1. But even though [1c] and [1¯a] are both “true” (probability 1) con-

sequences of the initial data, one cannot think of them as representing properties

of the particle which are simultaneously true in the same sense one is accustomed

to when thinking about classical systems, for there is no property corresponding

to [1c] AND [1¯a], just as there is no property corresponding to S

=+1/2 AND

=+1/2 for a spin-half particle.

The conceptual difﬁculty goes away if one supposes that the two incompatible

frameworks are being used to describe two distinct physical systems that are de-

scribed by the same initial data, or the same system during two different runs of

an experiment. In the case of two separate but identical systems, each with Hilbert

space H, the combination is described by a tensor product H ⊗ H, and employing

for the ﬁrst and F

for the second is formally the same as a single consistent

family for the combination. This is analogous to the fact that while S

=+1/2

AND S

=+1/2 for a spin-half particle is quantum nonsense, there is no problem

with the statement that S

=+1/2 for one particle and S

=+1/2 for a different

particle. In the same way, different experimental runs for a single system must oc-

cur during different intervals of time, and the tensor product

H (

H of two history

Hilbert spaces plays the same role as H ⊗ H for two distinct systems.

Incompatible frameworks do give rise to conceptual problems when one tries to

apply them to the same system during the same time interval. To be sure, there

is never any harm in constructing as many alternative descriptions of a quantum

system as one wants to, and writing them down on the same sheet of paper. The

difﬁculty comes about when one wants to think of the results obtained using incom-

patible frameworks as all referring simultaneously to the same physical system, or

tries to combine the results of reasoning based upon incompatible frameworks. It

is this which is forbidden by the single-framework rule of quantum reasoning.

Note, by the way, that in view of the internal consistency of quantum reasoning

discussed in Sec. 16.3, it is never possible, even using incompatible frameworks,

to derive contradictory results starting from the same initial data. Thus for the

example in Sec. 16.2, the fact that there is a framework in which one can conclude

with certainty that the particle is at the site 1c at t = 1 means there cannot be

another framework in which one can conclude that the particle is someplace else at

t = 1, or that it can be at site 1c with some probability less than 1. Any framework

which contains both the initial data and the possibility of discussing whether the

particle is or is not at the site 1c at t = 1 will lead to precisely the same conclusion

as F

. This does not contradict the fact that in F

the particle is predicted to be

in a state [1¯a]att = 1: F

does not contain [1c], and thus in this framework one

cannot address the question of whether the particle is at the site 1c at t = 1.

226 Quantum reasoning

Even though the single-framework rule tells us that the result [1c] from frame-

work F

and the result [1¯a]fromF

cannot be combined or compared, this state of

affairs is intuitively rather troubling, for the following reason. In classical physics

whenever one can draw the conclusion through one line of reasoning that a system

has a property P, and through a different line of reasoning that it has the property

Q, then it is correct to conclude that the system possesses both properties simulta-

neously. Thus if P is true (assuming the truth of some initial data) and Q is also

true (using the same data), then it is always the case that P AND Q is true. By

contrast, in the case we have been discussing, [1c] is true (a correct conclusion

from the data) in F

,[1¯a] is true if we use F

, while the combination [1c] AND

[1¯a] is not even meaningful as a quantum property, much less true!

When viewed from the perspective of quantum theory, see Ch. 26, classical

physics is an approximation to quantum theory in certain circumstances in which

the corresponding quantum description requires only a single framework (or, which

amounts to the same thing, a collection of compatible frameworks). Thus the prob-

lem of developing rules for correct reasoning when one is confronted with a mul-

tiplicity of incompatible frameworks never arises in classical physics, or in our

everyday “macroscopic” experience which classical physics describes so well. But

this is precisely why the rules of reasoning which are perfectly adequate and quite

successful in classical physics cannot be depended upon to provide reliable con-

ceptual tools for thinking about the quantum domain. However deep-seated may

be our intuitions about the meaning of “true” and “false” in the classical realm,

these cannot be uncritically extended into quantum theory.

As probabilities can only be deﬁned once a sample space has been speciﬁed,

probabilistic reasoning in quantum theory necessarily depends upon the sample

space and its associated framework. As a consequence, if “true” is to be iden-

tiﬁed with “probability 1”, then the notion of “truth” in quantum theory, in the

sense of deriving true conclusions from initial data that are assumed to be true,

must necessarily depend upon the framework which one employs. This feature

of quantum reasoning is sometimes regarded as unacceptable because it is hard

to reconcile with an intuition based upon classical physics and ordinary everyday

experience. But classical physics cannot be the arbiter for the rules of quantum

reasoning. Instead, these rules must conform to the mathematical structure upon

which quantum theory is based, and as has been pointed out repeatedly in previ-

ous chapters, this structure is signiﬁcantly different from that of a classical phase

space. To acquire a good “quantum intuition”, one needs to work through vari-

ous quantum examples in which a system can be studied using different incom-

patible frameworks. Several examples have been considered in previous chapters,

and there are some more in later chapters. I myself have found the example of

a beam splitter insider a box, Fig. 18.3 on page 253, particularly helpful. For

16.4 Interpretation of multiple frameworks 227

additional comments on multiple incompatible frameworks, see Secs. 18.4 and

27.3.

Measurements I

17.1 Introduction

I place a tape measure with one end on the ﬂoor next to a table, read the height

of the table from the tape, and record the result in a notebook. What are the

essential features of this measurement process? The key point is the establish-

ment of a correlation between a physical property (the height) of a measured sys-

tem (the table) and a suitable record (in the notebook), which is itself a physical

property of some other system. It will be convenient in what follows to think

of this record as part of the measuring apparatus, which consists of everything

essential to the measuring process apart from the measured system. Human be-

ings are not essential to the measuring process. The height of a table could be

measured by a robot. In the modern laboratory, measurements are often carried

out by automated equipment, and the results stored in a computer memory or on

magnetic tape, etc. While scientiﬁc progress requires that human beings pay atten-

tion to the resulting data, this may occur a long time after the measurements are

completed.

In this and the next chapter we consider measurements as physical processes

in which a property of some quantum system, which we shall usually think of as

some sort of “particle”, becomes correlated with the outcome of the measurement,

itself a property of another quantum system, the “apparatus”. Both the measured

system and the apparatus which carries out the measurement are to be thought of

as parts of a single closed quantum mechanical system. This makes it possible to

apply the principles of quantum theory developed in earlier chapters. There are

no special principles which apply to measurements in contrast to other quantum

processes. We need an appropriate Hilbert space for the measured system plus

apparatus, some sort of initial state, unitary time development operators, and a

suitable framework or consistent family of histories. There are, as always, many

228

17.1 Introduction 229

possible frameworks. A correct quantum description of the measuring process

must employ a single framework; mixing results from incompatible frameworks

will only cause confusion.

In practice it is necessary to make a number of idealizations and approximations

in order to discuss measurements as quantum mechanical processes. This should

not be surprising, for the same is true of classical physics. For example, the mo-

tion of the planets in the solar system can be described to quite high precision by

treating them as point masses subject to gravitational forces, but of course this is

not an exact description. The usual procedure followed by a physicist is to ﬁrst

work out an approximate description of some situation in order to get an idea of

the various magnitudes involved, and then see how this ﬁrst approximation can

be improved, if greater precision is needed, by including effects which have been

ignored. We shall follow this approach in this and the following chapter, some-

times pointing out how a particular approximation can be improved upon, at least

in principle. The aim is physical insight, not a precise formalism which will cover

all cases.

Quantum measurements can be divided into two broad categories: nondestruc-

tive and destructive. In nondestructive measurements, also called nondemolition

measurements, the measured property is preserved, so the particle has the same,

or almost the same property after the measurement is completed as it had be-

fore the measurement. While it is easy to make nondestructive measurements on

macroscopic objects, such as tables, nondestructive measurements of microscopic

quantum systems are much more difﬁcult. Even when a quantum measurement is

nondestructive for a particular property, it will be destructive for many other prop-

erties, so that the term nondestructive can only be deﬁned relative to some prop-

erty or properties, and does not refer to all conceivable properties of the quantum

system.

In destructive measurements the property of interest is altered during the mea-

surement process, often in an uncontrolled fashion, so that after the measurement

the particle no longer has this property. For example, the kinetic energy of an en-

ergetic particle can be measured by bringing it to rest in a scintillator and ﬁnding

the amount of light produced. This tells one what the energy of the particle was

before it entered the scintillator, whereas at the end of the measurement process

the kinetic energy of the particle is zero. In this and other examples of destructive

measurements it is clear that the correlation of interest is between a property the

particle had before the measurement took place, and the state of the apparatus after

the measurement, and thus involves properties at two different times. The absence

of a systematic way of treating correlations involving different times, except in

very special cases, is the basic reason why the theory of measurement developed

by von Neumann, Sec. 18.2, is not very satisfactory.

230 Measurements I

17.2 Microscopic measurement

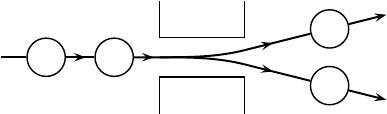
The measurement of the spin of a spin-half particle illustrates many of the princi-

ples of the quantum theory of measurement, so we begin with this simple case, us-

ing a certain number of approximations to keep the discussion from becoming too

complicated. Consider a neutral spin-half particle, e.g., a silver atom in its ground

state, moving through the inhomogeneous magnetic ﬁeld of a Stern–Gerlach appa-

ratus, shown schematically in Fig. 17.1. We shall assume the magnetic ﬁeld is such

that if the z-component S

of the spin is +1/2, there is an upwards force on the par-

ticle, and it emerges from the magnet moving upwards, whereas if S

=−1/2, the

force is in the opposite direction, and the particle moves downward as it leaves the

magnet.

ω ω



−

Fig. 17.1. Spin-half particle passing through a Stern–Gerlach magnet.

This can be described in quantum mechanical terms as follows. The spin states

of the particle corresponding to S

=±1/2are|z

 and |z

−

 in the notation of

Sec. 4.2. Let t

and t

be two successive times preceding the moment at which

the particle enters the magnetic ﬁeld, see Fig. 17.1, and t

a later time after it has

emerged from the magnetic ﬁeld. Assume that the unitary time development from

to t

is given by

|ω%→|z

|ω



%→|z

|ω

,

−

|ω%→|z

−

|ω



%→|z

−

|ω

−

,

(17.1)

where |ω, |ω



, |ω

−

 are wave packets for the particle’s center of mass, at

the locations indicated in Fig. 17.1. (One could also write these as ω(r), etc.)

One can think of the center of mass of the particle as the “apparatus”. The

two possible outcomes of the measurement are that the particle emerges from the

magnet in one of the two spatial wave packets |ω

 or |ω

−

. It is important that the

outcome wave packets be orthogonal,

ω

|ω

−

=0, (17.2)

as otherwise we cannot speak of them as mutually-exclusive possibilities. This

condition will be fulﬁlled if the wave packets have negligible overlap, as suggested

by the sketch in Fig. 17.1.

17.2 Microscopic measurement 231

In calculating the unitary time development in (17.1) we assume that the Hamil-

tonian for the particle includes an interaction with the magnetic ﬁeld, and this ﬁeld

is assumed to be “classical”; that is, it provides a potential for the particle’s mo-

tion, but does not itself need to be described using an appropriate ﬁeld-theoretical

Hilbert space. Similarly, we have omitted from our quantum description the atoms

of the magnet which actually produce this magnetic ﬁeld. These “inert” parts of the

apparatus could, in principle, be included in the sort of quantum description dis-

cussed in Sec. 17.3, but this is an unnecessary complication, since their essential

role is included in the unitary time development in (17.1).

The process shown in Fig. 17.1 can be thought of as a measurement because

the value of S

before the measurement, the property being measured, is correlated

with the spatial wave packet of the particle after the measurement, which forms the

output of the measurement. It is also the case that S

before the measurement is

correlated with its value after the measurement, and this means the measurement is

nondestructive for the properties S

=±1/2. One can easily imagine a destructive

version of the same measurement by supposing that the wave packets emerging

from the ﬁeld gradient of the main magnet pass through some regions of uniform

magnetic ﬁeld, which do not affect the center of mass motion, but do cause a pre-

cession of the spin. Consequently, at the end the process the location of the wave

packet for the center of mass will still serve to indicate the value of S

before the

measurement began, even though the ﬁnal value of S

need not be the same as the

initial value.

Suppose that the initial spin state is not one of the possibilities S

=±1/2, but

instead

=



+|z

−



√

2 (17.3)

corresponding to S

=+1/2. What happens during the measuring process? The

unitary time development of the initial state

|ψ

=|x

|ω=



|ω+|z

−

|ω



√

2 (17.4)

is obtained by taking a linear combination of the two cases in (17.1):

|ψ

%→|x

|ω



%→



|ω

+|z

−

|ω

−



√

2. (17.5)

The unitary history in (17.5) cannot be used to describe the measuring process,

because the measurement outcomes, |ω

 and |ω

−

, are clearly incompatible with

the ﬁnal state in (17.5). A quantum mechanical description of a measurement with

particular outcomes must, obviously, employ a frameworkin which these outcomes

are represented by appropriate projectors, as in the consistent family whose support

232 Measurements I

consists of the two histories

[ψ

] ( [x

][ω



] (



][ω

−

][ω

−

(17.6)

The notation, see (14.12), indicates that the two histories are identical at the times

and t

, but contain different events at t

. While this family contains the measure-

ment outcomes [ω

] and [ω

−

], it is still not satisfactory for discussing the process

in Fig. 17.1 as a measurement, because it does not allow us to relate these outcomes

to the spin states [z

] and [z

−

] of the particle before the measurement took place.

Since the properties S

=±1/2 are incompatible with a spin state [x

]att

, (17.6)

does not allow us to say anything about S

before the particle enters the magnetic

ﬁeld gradient. It is true that S

at t

is correlated with the measurement outcome if

we use (17.6). But this would also be true if the apparatus had somehow produced

a particle in a certain spin state without any reference to its previous properties,

and calling that a “measurement” would be rather odd.

A more satisfactory description of the process in Fig. 17.1 as a measurement is

obtained by using an alternative consistent family whose support is the two histo-

ries

[ψ

] (



][ω



] ( [z

][ω

−

][ω



] ( [z

−

][ω

−

(17.7)

As both histories have positive weights, one sees that

Pr(z

| ω

) = 1 = Pr(z

−

| ω

−

Pr(ω

| z

) = 1 = Pr(ω

−

| z

−

(17.8)

where we follow our usual convention that square brackets can be omitted and

subscripts refer to times: e.g., z

is the same as [z

]

and means S

=+1/2at

. (In addition, the initial state ψ

could be included among the conditions, but, as

usual, we omit it.) These conditional probabilities tell us that if the measurement

outcome is ω

at t

, we can be certain that the particle had S

=+1/2att

, and

vice versa; likewise, ω

−

at t

implies S

=−1/2att

. (For an initial spin state

 the conditional probabilities involving z

−

and ω

−

are undeﬁned, and those

involving z

and ω

are undeﬁned for an initial |z

−

.)

It is (17.8) which tells us that what we have been referring to as a measurement

process actually deserves that name, for it shows that the result of this process is a

correlation between speciﬁc outcomes and appropriate properties of the measured

system before the measurement took place. If these probabilities were slightly less

than 1, it would still be possible to speak of an approximate measurement, and in

practice all measurements are to some degree approximate.

17.3 Macroscopic measurement, ﬁrst version 233

In conclusion it is worth emphasizing that in order to describe a quantum pro-

cess as a measurement it is necessary to employ a framework which includes both

the measurement outcomes (pointer positions) and the properties of the measured

system before the measurement took place, by means of suitable projectors. These

requirements are satisﬁed by (17.7), whereas (17.6), even though it is an improve-

ment over a unitary family, cannot be used to derive the correlations (17.8) that are

characteristic of a measurement.

17.3 Macroscopic measurement, ﬁrst version

If the results are to be of use to scientists, measurements of the properties of mi-

croscopic quantum systems must eventually produce macroscopic results visible to

the eye or at least accessible to the computer. This requires devices that amplify

microscopic signals and produce some sort of macroscopic record. These pro-

cesses are thermodynamically irreversible, and this irreversibility contributes to the

permanence of the resulting records. Thus even though the production of certain

correlations, which is the central feature of the measuring process, can occur on a

microscopic scale, as discussed in the previous section, macroscopic systems must

be taken into account when quantum theory is used to describe practical measure-

ments. A full and detailed quantum mechanical description of the processes going

on in a macroscopic piece of apparatus containing 10

particles is obviously not

possible. Nonetheless, by making a certain number of plausible assumptions it is

possible to explore what such a description might contain, and this is what we shall

do in this and the next section, for a macroscopic version of the measurement of

the spin of a spin-half particle.

Once again, assume that the particle passes through a magnetic ﬁeld gradient,

Fig. 17.1, which splits the center of mass wave packet into two pieces which are

eventually separated by a macroscopic distance. The macroscopic measurement is

then completed by adding particle detectors to determine whether the particle is in

the upper or lower beam as it leaves the magnetic ﬁeld. One could, for example,

suppose that light from a laser ionizes a silver atom as it travels along one of the

paths emerging from the apparatus, and the resulting electron is accelerated in an

electric ﬁeld and made to produce a macroscopic current by a cascade process.

Detection of single atoms in this fashion is technically feasible, though it is not

easy. Of course, one must expect that in such a measurement process the spin

direction of the atom will not be preserved; indeed, the atom itself is broken up by

the ionization process. Hence such a measurement is destructive.

Let us assume once again that three times t

, t

, and t

are used in a quantum

description of the measurement process. The times t

and t

precede the entry of

the particle into the magnetic ﬁeld, Fig. 17.1, whereas t

is long enough after the