Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

29 Systems of particles

c.m.

Figure 1.14.

First consider the force acting on particle C due to particles A and B. In accordance with

Newton’s law of gravitation, the vertical components add to give

=−

√

3 Gm

=−

√

3 r

(1.162)

since l

√

3 r

. From the radial equation of motion for particle C we obtain

= F

√

3 r

(1.163)

Thus, we obtain the angular velocity



√

3 r



1/2



3Gm



1/2

(1.164)

Now let us assume the initial conditions r(0) = r

r(0) = 0,ω(0) =

. We can use

conservation of energy and of angular momentum to solve for the minimum value of r, and

therefore of l. Let us concentrate on particle C alone since the system values are three times

those of a single particle. The potential energy can be obtained by ﬁrst recalling that the

radial force

=−

∂V

∂r

=−

√

3 r

(1.165)

which can be integrated to yield the general expression

V =−

√

3 r

(1.166)

where the integration constant is set equal to zero.

30 Introduction to particle dynamics

When r = r

min

we have

r = 0 so the kinetic energy of particle C has the form

T =

(1.167)

Then, noting the initial conditions, the conservation of energy results in

T + V =

−

√

3 r

−

√

3 r

(1.168)

Conservation of angular momentum about the center of mass is expressed by the equation

H = mr

ω =

(1.169)

Hence

ω =

2 r

(1.170)

Now substitue for ω from (1.170) into (1.168) and use (1.164). After some algebraic sim-

pliﬁcation we obtain the quadratic equation

− 8r

r +r

= 0 (1.171)

which has the roots

1,2

= r

(1.172)

one of which is the initial condition. Thus

min

and l

min

(1.173)

Friction

Systems with friction are characterized by the loss of energy due to relative motion of the

particles. Thus, in general, they are not conservative. The two principal types of frictional

forces to be considered here are linear damping and Coulomb friction.

Linear damping

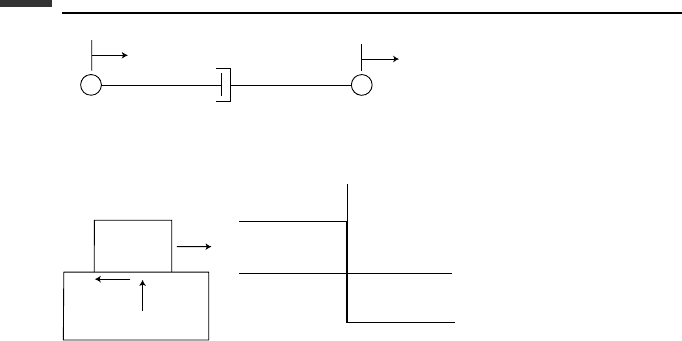
A linear viscous damper with a damping coefﬁcient c is shown connected between two

particles in Fig. 1.15. It is assumed to be massless and produces a tensile force proportional

to the relative separation rate of the particles in accordance with the equation

= c (

−

) (1.174)

In other words, the damper force always opposes any relative motion of the particles and

therefore does negative work on the system, dissipating energy whenever a relative velocity

exists.

31 Systems of particles

Figure 1.15.

(a) (b)

µN

−µN

Figure 1.16.

Coulomb friction

A Coulomb friction force is dissipative, like other friction forces, but is nonlinear; that is,

the friction force is a nonlinear function of the relative sliding velocity. As an example,

suppose that block A slides with velocity v

relative to block B, as shown in Fig. 1.16. The

force of block B acting on block A has a positive normal component N and a tangential

friction component µN , where the coefﬁcient of sliding friction µ is independent of the

relative sliding velocity v

. In detail, the Coulomb friction force is

=−µN sgn(v

) (1.175)

where F

and v

are positive in the same direction and where sgn(v

) equals ± 1, depending

on the sign of v

. Note that F

is independent of the contact area.

In the case v

= 0, that is, for no sliding, the force of friction can have any magnitude

less than that required to initiate sliding. The actual force in this case is obtained from the

equations of statics. Although the force required to begin sliding is actually slightly larger

than that required to sustain it, we shall ignore this difference and assume that F

as a

function of v

is given by Fig. 1.16b or (1.175).

Since the magnitude |F

|≤µN , we see that the direction of the total force of block B

acting on block A cannot deviate from the normal to the sliding surface by more than an

angle φ where

tan φ = µ (1.176)

This leads to the idea of a cone of friction having a semivertex angle φ. The total force

vector must lie on or within the cone of friction. It lies on the cone during sliding.

32 Introduction to particle dynamics

Figure 1.17.

Example 1.8 Two blocks, each of mass m, are connected by a linear damper and spring

in series, as shown in Fig. 1.17. They can slide without friction on a horizontal plane. First,

we wish to derive the differential equations of motion.

Using Newton’s law of motion, we ﬁnd that the x

equation is

= c(

−

) (1.177)

Similarly, the x

equation is

= k(x

− x

) (1.178)

We note that the forces in the damper and spring are equal, so we obtain the ﬁrst-order

equation

c (

−

) = k (x

− x

) (1.179)

These are the three linear differential equations of motion. They are equivalent to ﬁve

ﬁrst-order equations, so the total order of the system is ﬁve.

This system is unusual because the coordinate x

, which is associated with the connecting

point P between the damper and spring, does not involve displacement of any mass. This

results in an odd total order of the system rather than the usual even number. It is also

reﬂected in the degree of the characteristic equation and in the required number of initial

conditions.

Second method Let us assume the initial conditions

(0) = 0, x

(0) = 0 (1.180)

and

(0) = 0,

(0) = v

(1.181)

We see from (1.179) that

(0) = 0.

The analysis of this system can be simpliﬁed if we notice that the center of mass moves

at a constant velocity

due to conservation of linear momentum. Thus, a frame moving

with the center of mass is an inertial frame, and Newton’s laws of motion apply relative

to this frame. Let us use the coordinates x

, x

for positions relative to the center of

mass frame and assume that the origins of the two frames coincide at t = 0. Then we have

the initial conditions

(0) = 0, x

(0) = 0 (1.182)

33 Systems of particles

and

(0) =

(0) =−

(0) =

(1.183)

In general, x

and x

move as mirror images about the center of mass, so we can take

=−x

(1.184)

and simplify by writing equations of motion for x

and x

only as dependent variables.

We obtain, similar to (1.178) and (1.179),

+ kx

− kx

= 0 (1.185)

+ c

− kx

+ kx

= 0 (1.186)

To obtain some idea of the nature of the system response, we can assume solutions of

the exponential form e

, and obtain the resulting characteristic equation which turns out

to be a cubic polynomial in s. One root is zero and the other two have negative real parts.

Thus, the solutions for x

and x

each consist of two exponentially decaying functions of

time plus a constant. As time approaches inﬁnity, the exponential functions will vanish with

= x

and no force in the spring or damper. The length of the linear damper, however,

will have increased by 2x

compared with its initial value.

Finally, to obtain the solutions in the original inertial frame, we use

=−x

t (1.187)

= x

t (1.188)

= x

t (1.189)

Thus, in their ﬁnal motion, the blocks each move with a velocity

and a separation

somewhat larger than the original value.

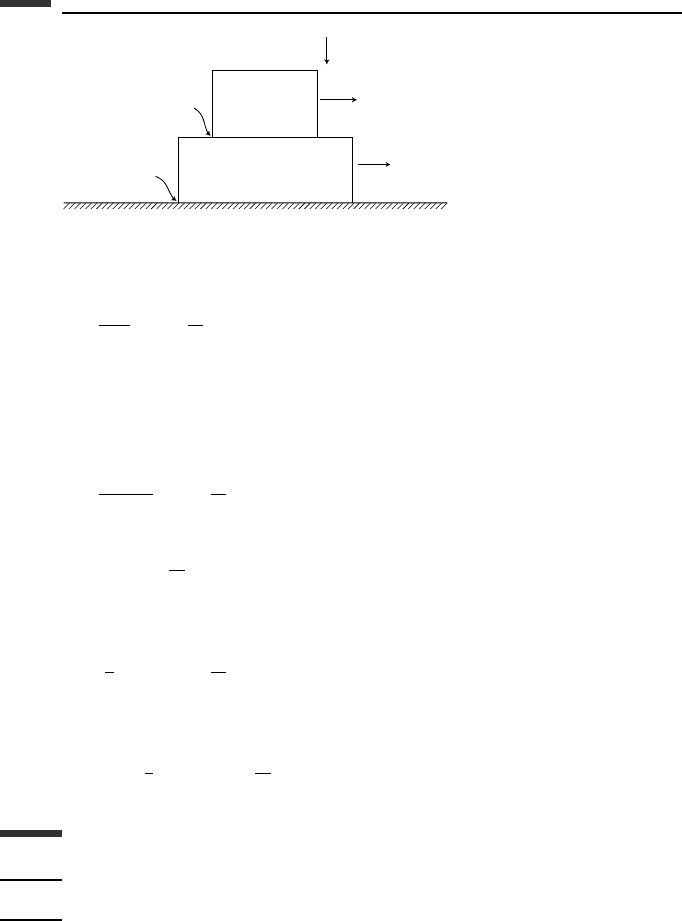
Example 1.9 Two stacked blocks, each of mass m, slide relative to each other as they

move along a horizontal ﬂoor, as shown in Fig. 1.18. Suppose that the initial conditions

are x

(0) = 0,

(0) = v

, x

(0) = 0,

(0) = 0. We wish to solve for the time when

sliding stops and the ﬁnal positions of the blocks, assuming a coefﬁcient of friction µ = 0.5

between the two blocks, and µ = 0.1 between block B and the ﬂoor.

The Coulomb friction force between blocks A and B is 0.5mg whereas the friction force

between block B and the ﬂoor is 0.2mg. The friction forces oppose relative motion so the

initial accelerations of blocks A and B are

=−0.5g (1.190)

= (0.5 − 0.2)g = 0.3g (1.191)

34 Introduction to particle dynamics

µ = 0.1

µ = 0.5

Figure 1.18.

Thus the relative acceleration between blocks A and B is 0.8g and the time to stop sliding

0.8g

= 1.25

(1.192)

At this time the common velocity of the two blocks is

= 0.375v

(1.193)

When t > t

, A and B will slide as a single block of mass 2m with an acceleration equal

to −0.1g. The stopping time for this combination is

0.375v

0.1g

= 3.75

(1.194)

Thus the time required for sliding to stop completely is

t = t

+ t

= 5

(1.195)

The ﬁnal displacement of block B is equal to its average velocity multiplied by the total

time. We obtain

t = 0.9375

(1.196)

The ﬁnal displacement of block A is equal to x

plus the displacement of A relative

to B.

= x

= 1.5625

(1.197)

1.3 Constraints and conﬁguration space

Generalized coordinates and conﬁguration space

Consider a system of N particles. The conﬁguration of this system is speciﬁed by giving

the locations of all the particles. For example, the inertial location of the ﬁrst particle

might be given by the Cartesian coordinates (x

, x

), the location of the second particle

by (x

, x

), and so forth. Thus, the conﬁguration of the system would be given by

35 Constraints and conﬁguration space

, x

,...,x

). In the usual case, the particles cannot all move freely but are at least

somewhat constrained kinematically in their differential motions, if not in their large motions

as well. Under these conditions, it is usually possible to give the conﬁguration of the system

by specifying the values of fewer than 3N parameters. These n ≤ 3N parameters are called

generalized coordinates (qs) and are related to the xsbythetransformation equations

= x

, q

,...,q

, t)(k = 1,...,3N ) (1.198)

The qs are not necessarily uniform in their dimensions. For example, the position of a

particle in planar motion may be expressed by the polar coordinates (r,θ) which have

differing dimensions. Thus, generalized coordinates may include common coordinate

systems. However, a generalized coordinate may also be chosen such that it is not identiﬁed

with any of the common coordinate systems, but represents a displacement form or shape

involving several particles. In this case, the generalized coordinate is deﬁned assuming

certain displacement ratios and relative directions among the particles. For example, a

generalized coordinate might consist of equal radial displacements of particles at the

vertices of an equilateral triangle.

Frequently one attempts to ﬁnd a set of independent generalized coordinates, but this

is not always possible. So, in general, we assume that there are m independent equations

of constraint involving the qs and possibly the

qs. If, for the same system, there are l

independent equations of constraint involving the 3Nxs (and possibly the corresponding

xs), then

3N − l = n − m (1.199)

and this is equal to the number of degrees of freedom. The number of degrees of freedom

is, in general, a property of the system and not of the choice of coordinates.

Since the conﬁguration of a system is speciﬁed by the values of its n generalized coordi-

nates, one can represent any particular conﬁguration by a point in n-dimensional conﬁgu-

ration space (Fig. 1.19). If the values of all the qs and

qs are known at some initial time t

then, as time proceeds, the conﬁguration point C will trace a solution path in conﬁguration

space in accordance with the dynamical equations of motion and any constraint equations.

For the case of independent qs, the curve will be continuous but otherwise not constrained.

If, however, there are holonomic constraints expressed as functions of the qs and possibly

time, then the solution point must remain on a hypersurface having fewer than n dimensions,

and which may be moving and possibly changing shape. In general, then, one can represent

an evolving mechanical system by an n-dimensional vector q, drawn from the origin to the

conﬁguration point C, tracing a path in conﬁguration space as time proceeds. This will be

discussed further in Chapter 2.

Holonomic constraints

Suppose that the conﬁguration of a system is speciﬁed by n generalized coordinates

,..., q

) and assume that there are m independent equations of constraint of the form

,..., q

, t) = 0(j = 1,..., m) (1.200)

36 Introduction to particle dynamics

Figure 1.19.

A constraint of this form is called a holonomic constraint. A dynamical system whose

constraint equations, if any, are all of the holonomic form is called a holonomic system.

An example of a holonomic constraint is provided by a particle which is forced to move

on a sphere of radius R centered at the origin of a Cartesian frame. In this case the equation

of constraint is

= x

+ y

+ z

− R

= 0 (1.201)

where (x, y, z) is the location of the particle. The sphere is a two-dimensional constraint

surface which is embedded in a three-dimensional Cartesian space.

The conﬁguration of a holonomic system can always be speciﬁed using a minimal set of

generalized coordinates equal in number to the degrees of freedom. This is also the number

of dimensions of the constraint hypersurface, that is, n − m. Hence it is always possible

in theory to ﬁnd a set of independent qs describing a holonomic system. For the case of a

spherical constraint surface, one could use angles of latitude and longitude to describe the

position of a particle. Another possibility might be to use the cylindrical coordinates φ and

z as qs, where φ effectively gives the longitude and z the latitude.

Nonholonomic constraints

Nonholonomic constraints may have the general form

(q,

q, t) = 0(j = 1,..., m) (1.202)

but usually they have a simpler form which is linear in the velocities. Thus, we nearly

always assume that nonholonomic constraints have the form



i=1

(q, t)

+ a

(q, t) = 0(j = 1,..., m) (1.203)

37 Constraints and conﬁguration space

or the alternate differential form



i=1

(q, t) dq

+ a

(q, t) dt = 0(j = 1,..., m) (1.204)

where, in either case, these expressions are not integrable. If either expression were inte-

grable, then a function φ

(q, t) would exist and (1.200) would apply, indicating that the

constraint is actually holonomic. In this case, we would have

(q,

q, t) =



i=1

∂φ

∂q

∂φ

∂t

= 0 (1.205)

and, comparing (1.203) and (1.205), we ﬁnd that

≡

∂φ

∂q

, a

≡

∂φ

∂t

(i = 1,...,n; j = 1,...,m) (1.206)

for this holonomic constraint. We conclude that holonomic and “linear” nonholonomic

constraints can be expressed in the forms of (1.203) and (1.204). The holonomic case

is distinguished by its integrability. Note that the coefﬁcients a

(q, t) and a

(q, t)are

generally nonlinear in the qs and t.

Other constraint classiﬁcations

A constraint is classed as scleronomic if the time t does not appear explicitly in the equation

of constraint. Otherwise, it is rheonomic. Thus, a scleronomic holonomic constraint has the

form

(q) = 0 (1.207)

A scleronomic nonholonomic constraint has the form



i=1

(q)

= 0 (1.208)

where we note that a

≡ 0.

Constraints having a

= 0, or a

= a

(q, t), or φ

= φ

(q, t) are classed as rheonomic

constraints. Typical examples of rheonomic constraints are a rod of varying length l(t)

connecting two particles in the holonomic case, or a knife edge whose orientation angle is

an explicit function of time in the nonholonomic case.

A catastatic constraint has ∂φ

/∂t ≡ 0 if holonomic, or a

≡ 0 if nonholonomic.

Catastatic constraints have an important place in dynamical theory. Note that all scleronomic

constraints are also catastatic, but not necessarily vice versa. For example, a nonholonomic

constraint having the form



i=1

(q, t)

= 0 (1.209)

is catastatic but is not scleronomic.

38 Introduction to particle dynamics

Dynamical systems can also be classiﬁed as scleronomic or rheonomic. A scleronomic

system satisﬁes the conditions that: (1) all constraints, if any, are scleronomic; and (2)

the transformation equations, given by (1.198), which relate inertial Cartesian coordinates

and generalized coordinates do not contain time explicitly. As an example illustrating the

importance of the second condition, consider a particle moving on a spherical surface,

centered at the origin, whose radius R(t) is a known function of time. We can use the

spherical coordinates θ and φ as independent generalized coordinates, that is, there are no

constraints on the qs. Hence, the ﬁrst condition is satisﬁed. The transformation equations,

however, are

x = R(t) sin θ cos φ

y = R(t ) sin θ sin φ (1.210)

z = R(t) cos θ

These transformation equations do not satisfy the second condition, so the system is rheo-

nomic.

Another classiﬁcation of dynamical systems involves the categories catastatic or

acatastatic. A catastatic system satisﬁes the conditions that: (1) all constraints, if any,

are catastatic; and (2) the system is capable of being continuously at rest by setting all the

qs equal to zero. This implies that ∂ x

/∂t ≡ 0fork = 1,...,3N ; that is, for all the trans-

formation equations. In other words, x

= x

(q) in agreement with the second condition

for a scleronomic system. Acatastatic means not catastatic.

Accessibility

Constraint equations, either holonomic or nonholonomic, are kinematic in nature; that is,

they put restrictions on the possible motions of a system, irrespective of the dynamical

equations. There is an important difference in these possible motions that distinguishes

holonomic from nonholonomic systems. It lies in the accessibility of points in conﬁguration

space. For the case of holonomic constraints, the conﬁguration point moves in a reduced

space of (n − m) dimensions since it must remain on each of m constraint surfaces, that is,

on their common intersection. Thus, certain regions of n-dimensional conﬁguration space

are no longer accessible.

By contrast, for nonholonomic constraints, it is the differential motions which are con-

strained. Since the differential equations representing these nonholonomic constraints are

not integrable, there are no ﬁnite constraint surfaces in conﬁguration space and there is

no reduction of the accessible region. In other words, by properly choosing the path, it is

possible to reach any point in n-dimensional q-space from any other point. As an exam-

ple, a scleronomic nonholonomic constraint, as given in (1.208), can be represented by an

(n − m)-dimensional planar differential surface element. Any differential displacement dq

must lie within that plane but is otherwise unconstrained. It is possible, however, to steer

the conﬁguration point C and its differential element to any point of conﬁguration space,

provided that more than one degree of freedom exists. A scleronomic system with only one