Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

19 Systems of particles

since, by Newton’s third law, the internal forces f

occur in equal, opposite, and collinear

pairs. Hence we obtain an equation of motion in the form



i=1

× F

= M

(1.102)

where M

is the applied moment about the ﬁxed point O due to forces external to the

system.

In a similar manner, if we differentiate (1.95) with respect to time, we obtain



i=1

× m

¨ρ

(1.103)

where ρ

is the position vector of the i th particle relative to the center of mass. From

Newton’s law of motion for the i th particle,

(

+ ¨ρ

) = F



j=1

(1.104)

Now take the vector product of ρ

with both sides of this equation and sum over i. We ﬁnd

that



i=1

× m

= 0 (1.105)

since



i=1

= 0 (1.106)

for a reference point at the center of mass. Also,



i=1



j=1

× f

= 0 (1.107)

because the internal forces f

occur in equal, opposite, and collinear pairs. Hence we obtain



i=1

× m

¨ρ



i=1

× F

= M

(1.108)

and, from (1.103) and (1.108),

= M

(1.109)

where M

is the external applied moment about the center of mass.

At this point we have found that the basic rotational equation

H = M (1.110)

applies in each of two cases: (1) the reference point is ﬁxed in an inertial frame; or (2) the

reference point is at the center of mass.

20 Introduction to particle dynamics

Finally, let us consider the most general case of an arbitrary reference point P. Upon

differentiating (1.98) with respect to time, we obtain

+ ρ

× m ¨ρ

= M

+ ρ

× m ¨ρ

(1.111)

But, from Newton’s law of motion for the system,

+ ¨ρ

) = F (1.112)

so we obtain

= M

+ ρ

× (F − m

) (1.113)

The applied moment about P is

= M

+ ρ

× F (1.114)

Thus, the rotational equation for this general case is

= M

− ρ

× m

(1.115)

We note immediately that this equation reverts to the simpler form of (1.110) if P is a ﬁxed

point (

= 0) or if P is located at the center of mass (ρ

= 0). The right-hand term also

vanishes if ρ

and

are parallel.

Accelerating frames

Consider a particle of mass m

and its motion relative to a noninertial reference frame

that is not rotating but is translating with point P at its origin (Fig. 1.10). The equation of

motion is

(

+ ¨ρ

) = F

(1.116)

where F

is now the total force acting on the particle. Relative to the accelerating frame,

the equation of motion has the form

¨ρ

= F

− m

(1.117)

The term −m

can be regarded as an inertia force due to the acceleration of the frame.

Note that the same equation of motion is obtained if we assume that the frame attached to

P is not accelerating, but instead there is a uniform gravitational ﬁeld with an acceleration

of gravity −

As another example of motion relative to an accelerating reference frame, consider again

the rotational equation given in (1.115). We can write it in the form

= M

−



i=1

× m

(1.118)

21 Systems of particles

since

mρ



i=1

(1.119)

gives the position ρ

of the center of mass. The last term of (1.118) can be interpreted as

the moment about P of individual inertia forces −m

that act on each particle m

,the

forces being parallel in the manner of an artiﬁcial gravitational ﬁeld. The total moment of

these inertial forces, as given in (1.115), is −ρ

× m

, which can be considered as a total

inertia force −m

acting at the center of mass.

The concept of inertia forces and an artiﬁcial gravitational ﬁeld due to an accelerating

reference frame can be expressed as the following principle of relative motion: All the

results and principles derivable from Newton’s laws of motion relative to an inertial frame

can be extended to apply to an accelerating but nonrotating frame if the inertia forces

associated with the acceleration of the frame are considered as additional forces acting

on the particles of the system. This important result is particularly useful if some reference

point in the system has an acceleration that is a known function of time. Note that it applies

to work and energy principles relative to the accelerating frame without having to solve for

the forces causing the acceleration.

Work and energy

The kinetic energy of a particle of mass m

moving with speed v

relative to an inertial

frame is

(1.120)

The total kinetic energy of a system of N particles is found by summing over the particles,

resulting in

T =



i=1



i=1

(1.121)

Let us use the notation that

≡

(1.122)

and assume a center of mass reference point such that

= r

+ ρ

(1.123)

The total kinetic energy can be written in the form

T =



i=1



i=1

(

+ ˙ρ

) ·(

+ ˙ρ

)



i=1

˙ρ

(1.124)

22 Introduction to particle dynamics

where we recall that



i=1

= 0 (1.125)

for this center of mass reference point. Equation (1.124) is an expression of Koenig’s

theorem: The total kinetic energy of a system of particles is equal to that due to the total

mass moving with the velocity of the center of mass plus that due to the motion of individual

particles relative to the center of mass.

As a further generalization, let us consider a system of particles with a general reference

point P (Fig. 1.10). Here we have

= r

+ ρ

(1.126)

and the total kinetic energy is

T =



i=1



i=1

(

+ ˙ρ

) ·(

+ ˙ρ

)



i=1

˙ρ

· m ˙ρ

(1.127)

We see that the total kinetic energy is the sum of three parts: (1) the kinetic energy due

to the total mass moving at the speed of the reference point; (2) the kinetic energy due

to motion relative to the reference point; and (3) the scalar product of the reference point

velocity and the linear momentum of the system relative to the reference point. Equation

(1.127) is an important and useful result. It is particularly convenient in the analysis of

systems having a reference point whose motion is known but which is not at the center of

mass.

Now let us look into the relationship between the work done on a system of particles

and its kinetic energy. We start with the equation of motion for the ith particle, as in (1.82),

namely,

= F



j=1

(1.128)

Assume that the ith particle moves over a path from A

to B

. Take the dot product of each

side with dr

and evaluate the corresponding line integrals. We obtain



· dr







dt =



− v



(1.129)

which is the increase in kinetic energy of the i th particle. The line integral on the right is







j=1



· dr

(1.130)

23 Systems of particles

which is the total work done on the ith particle by the external plus internal forces. Now

sum over all the particles. The total work done on the system is

W =



i=1



i=1







j=1



· dr

(1.131)

and the increase in the total kinetic energy is

− T



i=1



− v



(1.132)

Thus, equating the line integrals obtained from (1.128), we ﬁnd that

− T

= W (1.133)

This is the principle of work and kinetic energy: The increase in the kinetic energy of a

system of particles over an arbitrary time interval is equal to the work done on the system

by external and internal forces during that time. Since this principle applies continuously

to an evolving system, we see that

T =

W (1.134)

that is, the rate of increase of kinetic energy is equal to the rate of doing work by the forces

acting on the system.

If we choose a center of mass reference point, we have

= r

+ ρ

(1.135)

and the work done on the system can be written in the form

W =



F · dr



i=1







j=1



· dρ

(1.136)

where A

and B

are the end-points of the path followed by the center of mass. The equation

of motion for the center of mass is identical in form with that of a single particle; hence,

they will have similar work–energy relationships. Therefore, the work done by the total

external force F in moving through the displacement of the center of mass must equal the

increase in the kinetic energy associated with the center of mass motion, as given in the ﬁrst

term of (1.124). Then the remaining term in the work expression, representing the work of

the external and internal forces in moving through displacements relative to the center of

mass, must equal the increase in the kinetic energy of relative motions, that is, in the change

in the last term of (1.124).

Conservation of energy

Let us consider a particle whose position (x, y, z) is given relative to an inertial Cartesian

frame. Suppose that the work done on the particle in an arbitrary inﬁnitesimal displacement is

dW = F · dr = F

dx + F

dy + F

dz (1.137)

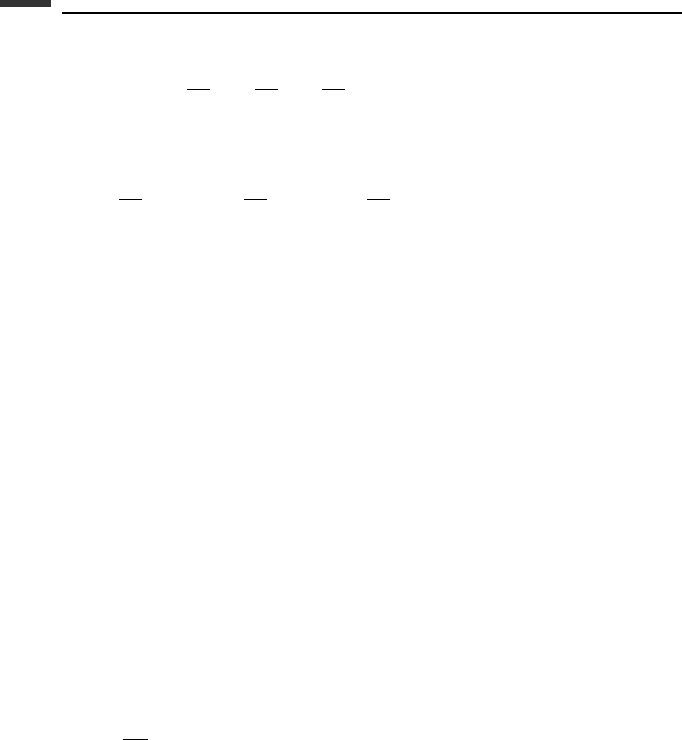
24 Introduction to particle dynamics

and the right-hand side is equal to the total differential of a function of position. Let us take

dW =−dV =−

∂V

∂x

dx −

∂V

∂y

dy −

∂V

∂z

dz (1.138)

where the minus sign is chosen for convenience and the potential energy function is

V (x, y, z). Then, since dr is arbitrary, we can equate coefﬁcients to obtain

=−

∂V

∂x

, F

=−

∂V

∂y

, F

=−

∂V

∂z

(1.139)

or, using vector notation,

F =−∇V (1.140)

that is, the force is equal to the negative gradient of V (x, y, z).

In accordance with the principle of work and kinetic energy, the increase in kinetic energy

dT = dW =−dV (1.141)

so we ﬁnd that

T +

V = 0 (1.142)

or, after integration with respect to time,

T + V = E (1.143)

where the total energy E is a constant. This is the principle of conservation of energy applied

to a rather simple system.

This principle can easily be extended to apply to a system of N particles whose positions

are given by the 3N Cartesian coordinates x

, x

,...,x

. In this case, the kinetic energy

T is the sum of the individual kinetic energies, and the overall potential energy V (x)isa

function of the particle positions. The force in the positive x

direction obtained from V is

=−

∂V

∂x

(1.144)

The system will be conservative, that is, the total energy T + V will be constant if it

meets the following conditions: (1) the potential energy V (x ) is a function of position only

and not an explicit function of time; and (2) all forces which do work on the system in

the actual motion are obtained from the potential energy in accordance with (1.144); any

constraint forces do no work. Later the concept of a conservative system will be extended

and generalized.

It sometimes occurs that the forces doing work on a system are all obtained from a

potential energy function of the more general form V (x, t ) by using (1.144) or (1.140).

In this case, the forces are termed monogenic, that is, derivable from a potential energy

function, whether conservative or not.

25 Systems of particles

(a)

(b)

(c)

Figure 1.11.

Example 1.4 Let us consider the form of the potential energy function in various common

cases.

Uniform gravity Suppose a particle of mass m is located at a distance y above a reference

level in the presence of a uniform gravitational ﬁeld whose gravitational acceleration is g,

as shown in Fig. 1.11a. The downward force acting on the particle is its weight

w = mg (1.145)

From (1.139) we obtain

=−

∂V

∂y

=−mg (1.146)

which can be integrated to yield the potential energy

V (y) = mgy (1.147)

The constant of integration has been chosen equal to zero in order to give zero potential

energy at the reference level.

Inverse-square gravity A uniform spherical body of mass m

and radius R exerts a gravi-

tational attraction on a particle of mass m located at a distance r from the center O,as

shown in Fig. 1.11b. The radial force on the particle has the form

=−

(r ≥ R) (1.148)

26 Introduction to particle dynamics

where K = Gm

m. The universal gravitational constant G has the value

G = 6.673 ×10

−11

N ·m

/kg

and we have used units of Newtons, meters, and kilograms. Equation (1.148) is a statement

of Newton’s law of gravitation where each attracting body is regarded as a particle. Using

(1.144) we obtain

−

∂V

∂r

=−

(1.149)

which integrates to

V (r) =−

(1.150)

and we note that the gravitational potential energy is generally negative, but goes to zero as

r →∞.

Linear spring A commonly encountered form of potential energy is that due to elastic

deformation. As an example, consider a particle P which is attached by a linear spring of

stiffness k to a ﬁxed point O, as shown in Fig. 1.11c. The force of the spring acting on the

particle is

=−

∂V

∂x

=−kx (1.151)

where x is the elongation of the spring, measured from its unstressed position. Integration

of (1.151) yields the potential energy

V (x) =

(1.152)

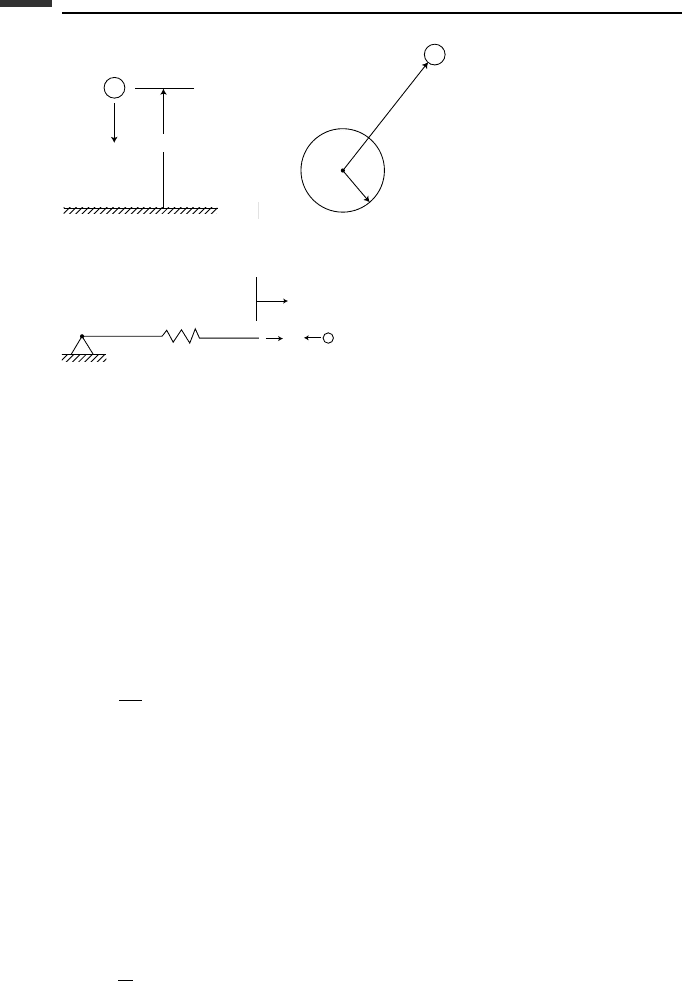
Example 1.5 A particle of mass m is displaced slightly from its equilibrium position

at the top of a smooth ﬁxed sphere of radius r , and it slides downward due to gravity

(Fig. 1.12). We wish to solve for its velocity as a function of position, and the angle θ at

which it loses contact with the sphere.

Rather than writing the tangential equation of motion involving

θ and then integrating,

we can solve directly for the velocity of the particle by using conservation of energy. We

see that

T =

(1.153)

and, using the center O as the reference level,

V = mgr cos θ (1.154)

Conservation of energy results in

T + V =

+ mgr cos θ = mgr (1.155)

27 Systems of particles

Figure 1.12.

and, solving for the velocity, we obtain

v =



2gr(1 − cos θ) (1.156)

Let N be the radial force of the sphere acting on the particle. The radial equation of motion

=−

= N − mg cos θ (1.157)

From (1.156) and (1.157) we obtain

N = mg (3 cos θ − 2) (1.158)

The particle leaves the sphere when the force N decreases to zero, that is, when

cos θ =

or θ = 48.19

◦

(1.159)

Example 1.6 Particles A and B, each of mass m, are connected by a rigid massless rod

of length l, as shown in Fig. 1.13. Particle A is restrained by a linear spring of stiffness k,

but can slide without friction on a plane inclined at 45

◦

with the horizontal. We wish to

obtain the differential equations for the planar motion of this system under the action of

gravity.

It will simplify matters if we can obtain the differential equations of motion without

having to solve for either the normal constraint force of the inclined plane acting on particle

A, or for the compressive force of the rod acting on both particles. First, let us write Newton’s

law for the motion of the center of mass in the x-direction. We obtain



x +

θ cos(θ − 45

◦

) −

sin(θ − 45

◦

)



=−kx + 2mg sin 45

◦

x +

√

θ(cos θ + sin θ) −

√

(sin θ − cos θ) =−kx +

√

2 mg (1.160)

28 Introduction to particle dynamics

45°

Figure 1.13.

where x is measured from the position of zero force in the spring. This is the x equation of

motion.

Next, let us write the rotational equation, using A as a reference point where A has

an acceleration

x down the plane. Thus, we must use (1.118) for motion relative to an

accelerating frame. This means that an inertia force m

x is applied at B and is directed

upward, parallel to the plane. Then, relative to A, the gravitational and inertial moments are

added. Thus, we obtain

H = ml

θ = mgl sin θ − ml

x cos(θ − 45

◦

)

θ +

√

x (cos θ + sin θ) = mgl sin θ (1.161)

This is the θ equation of motion.

Example 1.7 Three particles, each of mass m, are located at the vertices of an equilateral

triangle and are in plane rotational motion about the center of mass (Fig. 1.14). They

are subject to mutual pairwise gravitational attractions as the separation l = l

remains

constant. (a) Solve for the required angular velocity ω = ω

. (b) Now suppose that with

l = l

and

l = 0, the angular velocity is suddenly changed to

. Find the minimum

value of l in the ensuing motion, assuming that an equilateral conﬁguration is maintained

continuously.