Graziani F. (editor) Computational Methods in Transport

Подождите немного. Документ загружается.

438 A.V. Gichuk et al.

and the number of particles resultant from such collisions. With regard to

the transport operator approximation conservativeness, we obtain that the

proposed scheme is balanced both relative to particle transport and relative

to particle collisions.

Of great importance, from viewpoint of substantiation and application, is

the problem of the KM-method stability in time. Such stability can be roved

analytically for some partial cases.

3 MKM-method

In spite of some evident advantages of the KM method, it also has certain dis-

advantages, namely, there is a signiﬁcant increase in the number of iterations

when numerically solving 2D problems with grid fragmentation in optically

dense physical regions. One of the main assumptions made for the (4) of the

corrector phase is the approximate substitution:



j=1

s+1

∆ε

(0)

≈ 2π



j=1

s+1

∆ε

, (5)

that is valid (to a satisfactory precision) for processes with isotropic or almost

isotropic distribution of particles. In essentially anisotropic cases, the (5) has

to be speciﬁed. The implications above caused the development of the MKM-

method.

This method also has two phases, the ﬁrst of them (predictor) coincides

with (3). The diﬀerence between the two methods is in the corrector phase,

where two opposite directions of particle ﬂight (

→

Ω

and

→

Ω

−

) are considered

simultaneously. The second phase equations are:

s+1

∆ε

n+1

∆t

+ L

s+1

∆ε

n+γ

+ α

s+1

∆ε

n+γ

2π



j=1

s+1

∆ε

(0)

2π



j=1

⎛

⎝

s+1/2

(0)

−

(0)

⎞

⎠

, (6)

s+1

∆ε

−n+1

∆t

+ L

−

s+1

∆ε

−n+γ

+ α

s+1

∆ε

−n+γ

2π



j=1

s+1

∆ε

(0)

2π



j=1

⎛

⎝

s+1/2

(0)

−

(0)

⎞

⎠

. (7)

Here, corrections ∆ε and ∆ε correspond to directions

→

Ω

and

→

Ω

−

,the

same is true for diﬀerence transport operators. The mean ﬂux of particles

KM-Method of Iteration Convergence Acceleration 439

in the (7) can be expressed via the right-hand side and the incoming ﬂuxes

through the illuminated faces of a phase space cell. Set the incoming ﬂuxes

equal to zero for the correction function (corrector), this corresponds to the

assumption that ﬂuxes found during the ﬁrst half-step are used in this phase.

Using the approximate substitution

∆ε

(0)

≈ π



∆ε

+∆ε

−



(8)

from the (6) and (7) and equating the right-hand sides give us the correlation

factors

∆ε

−

= A

∆ε

+ B

the resultant formula (8) now looks like

∆ε

(0)

≈ π ((A

+1)∆ε

+ B

) . (9)

Substitution (9) in the (6) gives us the ﬁnal form of the second phase

(corrector) of the MKM-method:

s+1

∆ε

n+1

∆t

+ L

s+1

∆ε

n+γ

+ α

s+1

∆ε

n+γ

−



j=1

+1)

s+1

∆ε

n+γ



j=1

2π



j=1

⎛

⎝

s+1/2

(0)

−

(0)

⎞

⎠

, (10)

where A

and B

can be found by equating the left-hand sides of the (6) and

(7).

The values from the previous iteration are used in the oﬀered version of

the MKM-method to obtain the expression (9) for direction

→

Ω

,sothemethod

becomes non-conservative. There is a way to bypass the problem by solving

the (6) and (7) using the sweep method, however, this way leads to signiﬁcant

complication the computational algorithm.

4 KM3-method

As it was mentioned above, the practice of using the KM-method shows a

signiﬁcant increase of the number of iterations during numerical solution of

some classes of problems. For this reason, it becomes necessary to decrease

(subdivide) time steps in order to solve time-depend problems.

For the KM-method eﬃciency enhancement and further extension of the

range of multidimensional problems that can be solved using this method, its

new version called “KM3-method” is oﬀered in the paper. The main features

of the standard KM-method are preserved in the new scheme construction.

440 A.V. Gichuk et al.

The KM3-method’s speciﬁc feature is that it allows solving a three-phase sys-

tem of equations that provides signiﬁcant enhancement of its cost-eﬃciency

and less dependence of the number of iterations on the time step value.

Similar to KM- and MKM-methods, KM3-method is constructed using

the predictor-corrector scheme. The (3) is solved in the ﬁrst phase. The second

phase (corrector) has a more complicated structure, it includes two equations

in which the internal sub-iteration cycle is arranged, namely:

s+1,ν+1/2

∆ε

n+1

∆t

+ L

s+1,ν+1/2

∆ε

n+γ

+ α

s+1,ν+1/2

∆ε

n+γ

− l



j=1

s+1,ν+1/2

∆ε

n+γ

=(1− l)

2π



j=1

s+1,ν

∆ε

(0)

2π



j=1

⎛

⎝

s+1/2

(0)

−

(0)

⎞

⎠

s+1,0

∆ε

n+γ

s+1/2

∆ε

n+γ

, (11)

s+1,ν+1

∆

n+1

∆t

+ L

s+1,ν+1

∆

n+γ

+ α

s+1,ν+1

∆

n+γ

−



j=1

s+1,ν+1

∆

n+γ

=(1− l)

2π



j=1

s+1,ν+1/2

∆ε

(0)

− (1 − l)

2π



j=1

s+1,ν

∆ε

(0)

s+1,0

∆ε

s+1/2

∆ε

s+1

s+1/2

s+1,ν+1/2

∆ε

s+1,ν+1

∆

. (12)

Here, ν is a sub-iteration number with respect to the corrector phase steps,

l is parameter that may be dependent on the space grid’s cell geometry and

the energy group (generalizations to this approach are also possible, where

the angular dependence is assumed as well). If l = const, l ∈ (0; 1). Iterations

in ν can be performed either up to the speciﬁed precision achievement (∼10+

20%), or a certain number of times (∼3–5).

5 Test Computation Results

All the methods described above have been veriﬁed for radiation transport

problems. The corresponding transport equation system can be easily reduced

to the form (1) as a result of Planck function linearization with respect to

temperature using the energy equation.

KM-method

To demonstrate the method eﬃciency, the parameters of multiple-group Fleck

problem computations are given below. The problem geometry is shown in

Fig. 2.

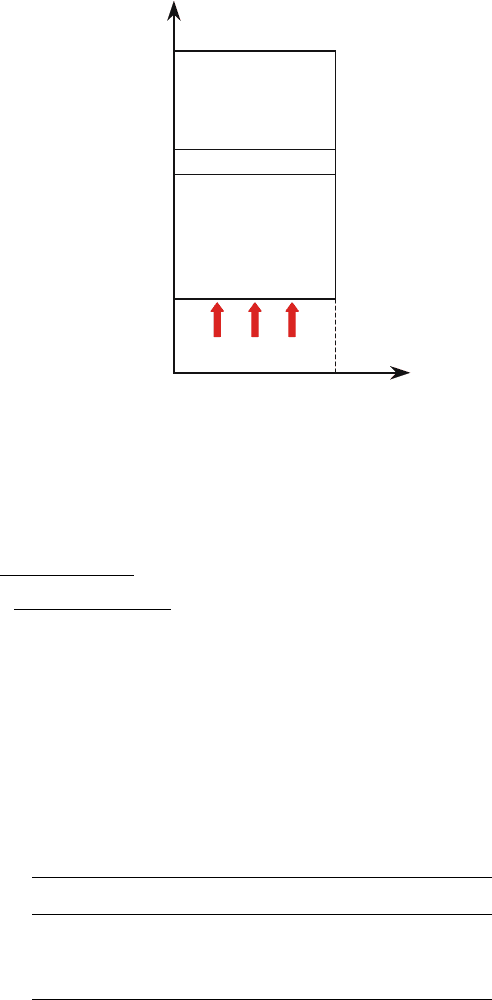
KM-Method of Iteration Convergence Acceleration 441

104

102.4

102

100

T=1 keV

16 x 3

20 x 3

Fig. 2. The spectral Fleck problem geometry

The material density in the system is ρ = 1, the material energy depen-

dence on temperature is described by equation E = T . Cross-sections:

= 0 is scattering cross-sections;

27(1−exp(−ω

/T ))

(optically transparent regions) and

10000(1−exp(−ω

/T ))

(optically dense region) are absorption cross-

sections.

The boundary condition “mirror reﬂection” is speciﬁed on the left {Z =

0; 100 ≤ R ≤ 104} and the right {Z = 1; 100 ≤ R ≤ 104} ends. The angular

grid is S

quadrature. The mean numbers of iterations in computations with

various time steps during the problem solution using the method of source

iterations and the KM-method are given in Table 1.

The radiation temperature distribution for ct = 30 is shown in Fig. 3.

Table 1. The mean number of iterations per 100 steps

c∆t, cm Source Iterations KM-method

0.03 166.92 11.91

0.15 1907.53 24.82

0.30 3961.35 40.48

442 A.V. Gichuk et al.

Fig. 3. The radiation temperature distribution, ct =30cm

Region 2 (10 100)

Region 1 (10 100)

1.2

Fig. 4. The geometry of the test problem with tube

MKM-method

The method was veriﬁed using the axially symmetric two-region one-group

problem of a tube which geometry is shown in Fig. 4.

The material density in the system is ρ = 1, the material energy de-

pendence on temperature is described by equation E =0.81 T . Photon ab-

sorption is taken into account in computations, with the photon absorption

cross-section being speciﬁed by the formula: χ

= A/T

. The optically dense

(region 1) and the optically transparent (region 2) regions are speciﬁed by

various values of A factor.

A =50.89 in region 1 (optically dense).

A =0.1374 in region 2 (optically transparent).

The absorption cross-section was set equal to zero in computations

(χ

= 0). The following boundary conditions with respect to radiation are

speciﬁed on the left end of the rectangular region {Z =0;1≤ R ≤ 1.2}:“mir-

ror reﬂection” for the boundary section belonging to the dense casing and the

incoming isotropic radiation ﬂux corresponding to temperature T = 1 for the

boundary section belonging to the transparent region. The incoming radia-

tion ﬂux was set equal to zero on the upper boundary and the right end.

The results of computations using the standard KM-method and the

MKM-method are compared (see Table 2).

KM-Method of Iteration Convergence Acceleration 443

Table 2. The number of iterations in regions

Number of Iterations

c∆t =0.3cm c∆t =1.5cm c∆t =3cm

Step No. KM MKM KM MKM KM MKM

5 13 23 13 25 31 100 36 93 49 100 61 100

10 12 26 12 26 26 100 31 100 30 100 51 100

15 11 26 11 27 23 93 27 94 18 100 41 100

20 15 25 11 26 14 89 24 83 13 100 30 100

25 10 25 10 27 12 85 21 77 11 100 20 100

30 826102512 8418 731010014 91

35 8 29 9 24 12 77 15 69 8 84 10 79

40 8 31 8 24 11 74 12 64 7 73 7 67

45 8 29 8 24 11 70 11 60 6 55 6 58

50 7 22 8 23 11 66 9 55 5 49 5 46

Table 3. The Number of Iterations in Regions

c∆t =0.3cm c∆t =1.5cm c∆t =3cm

Step No. SI KM KM3 SI KM KM3 SI KM KM3

1 19108 14 14 28696 26 26 26454 35 35

5 3332 24 20 6363 121 88 7960 238 174

10 1559 27 20 8477 101 75 9146 179 135

KM3-method

To demonstrate the method serviceability, the table below (Table 3) gives the

tube problem computation parameters for computations using the method of

source iterations (SI), KM- and KM3-methods. The test problem description

is given above.

A Regularized Boltzmann Scattering Operator

for Highly Forward Peaked Scattering

Anil K. Prinja

and Brian C. Franke

University of New Mexico, Chemical and Nuclear Engineering Department,

Albuquerque, NM 87131, USA

prinja@unm.edu

Sandia National Laboratories, P.O. Box 5800, MS 1179, Albuquerque, NM

87185

bcfrank@sandia.gov

1 Introduction

Extremely short collision mean free paths and near-singular elastic and

inelastic diﬀerential cross sections (DCS) make analog Monte Carlo and de-

terministic computational approaches impractical for charged particle trans-

port. The widely used alternative, the condensed history method, while

eﬃcient, also suﬀers from several limitations arising from the use of pre-

computed inﬁnite medium distributions for sampling particle directions and

energies. Accordingly, considerable attention has recently focused on the

development of computationally eﬃcient algorithms that implement the cor-

rect transport mechanics. Fokker-Planck [JEM81] and Boltzmann Fokker-

Planck [CL83] approximations have historically proved very useful in

handling highly peaked scattering in certain classes of problems but these

approaches are limited in the accuracy they can ultimately deliver. A more

general methodology that allows accuracy to be systematically increased

with practically no enhancement of algorithmic complexity has become pos-

sible with the advent of recently proposed higher order Fokker-Planck ex-

pansions [GCP96] and their implementation in so-called Generalized Fokker-

Planck models [LL01,PP01,PKH02]. The goal of these newer approaches is to

approximate the analog transport problem by one which is characterized by

longer or stretched mean free paths and nonsingular collision operators but

which can be solved numerically with considerably less eﬀort than the analog

problem and whose accuracy and eﬃciency can be readily adapted to a broad

class of problems. One such implementation that has proved particularly ef-

ﬁcient uses purely discrete scattering angle and hybrid discrete-continuous

scattering angle representations [FPKL1, FPKL2]. Moreover, generalizations

of these methodologies to describe energy-loss straggling have been success-

fully demonstrated [PKH02].

Here we describe an angular moment-preserving procedure to regular-

ize the near-singular collision integral for electron elastic scattering by

446 A.K. Prinja and B.C. Franke

approximating and then re-summing what we refer to as a generalized Fermi

expansion. It’s diﬀerence from the generalized Fokker-Planck expansion of

Leakeas and Larsen [LL01] will become apparent in the ensuing but we

note here that the advantage of using the formulation developed below is

that the resulting renormalized scattering kernel has a simple and explicit

form which lends itself to a convenient implementation in Monte Carlo sim-

ulations. Furthermore, unlike our recent discrete scattering angle formula-

tion [FPKL1,FPKL2], the present approach is continuous in scattering angle

and consequently is free of ray artifacts. The generalized Fermi expansion is

developed in the next section, followed by a presentation of the regularization

procedure. Numerical results are then presented and the paper closes with

some concluding remarks.

2 Generalized Fermi Expansion

Our approach consists of a modiﬁed use of earlier proposed higher-order

Fokker-Planck expansions to describe scattering that is strongly anisotropic

but not suﬃciently forward peaked that a strictly Fokker-Planck approxima-

tion can be justiﬁed [GCP96, LL01, PP01]. We note that this is invariably

the situation for realistic electron scattering interactions such as described

by the screened Rutherford cross section and its variants, but which never-

theless are near-singular at zero deﬂection. As will become apparent shortly,

our implementation amounts to approximating the angular diﬀusion Fokker-

Planck operator, which is just the Laplacian on the unit sphere, by a planar

Laplacian in this higher order expansion and it generalizes a result ﬁrst due

to Fermi [RG41].

We begin by writing the analog transport equation for the angular ﬂux

ψ(r, Ω) of electrons at spatial position r along direction Ω as

Ω ·∇ψ(r, Ω)=J[ψ],ψ(r

, Ω)=δ(1 − Ω

· Ω), n · Ω < 0 , (1)

where n is the outward directed unit normal at surface point r

and Ω

is the

incident beam direction. Also in (1), J[ψ], a linear functional of the angular

ﬂux, is the elastic scattering collision integral, and is given by:

J[ψ]=



4π

(Ω



· Ω) ψ(Ω



)dΩ



− σ

ψ(Ω) , (2)

where σ

(Ω



· Ω) is the diﬀerential elastic scattering cross section (DCS),

= Ω



· Ω is the cosine of the scattering angle, and σ

the correspond-

ing inverse scattering mean free path. Energy losses are neglected in the

present investigation but it has been demonstrated before that singular in-

elastic energy-loss operators can also be regularized [PKH02].

Since charged particle interactions are mediated by long range Coulomb

forces, the DCS σ

(Ω



·Ω) falls very sharply away from Ω



·Ω = 1, decreasing

Regularized Scattering Operator 447

in a continuous manner by several orders of magnitude over a scattering

angle range of only a few degrees. This has the consequence that an initially

peaked distribution will diﬀuse slowly in angle with increasing depth into

the material and it enables us to introduce two simplifying approximations.

First, we write

Ω



· Ω ≈ 1 −



(η − η



)

+(ξ − ξ



)



, (3)

where η and ξ are the x and y direction cosine components of Ω. Second, we

extend the domain of η and ξ to the open interval (−∞, ∞), a reasonable

step since the angular ﬂux decays rapidly away from the initial direction.

Using these results in (2) gives after some rearrangement

J[ψ]=



∞

−∞



∞

−∞

ˆσ

(η

2

+ ξ

2

) ψ(η − η



,ξ−ξ



)dη



dξ



− σ

ψ(η, ξ) , (4)

where ˆσ

(η

+ ξ

) ≡ σ

[1 − (η

+ ξ

)/2]. Our goal is to represent (4) as

a diﬀerential expansion and to that end we introduce the two dimensional

Fourier transform pair

ψ(k, l)=

2π



∞

−∞



∞

−∞

−iK·α

ψ(η, ξ)dηdξ , (5)

ψ(η, ξ)=

2π



∞

−∞



∞

−∞

iK·α

ψ(k, l)dkdl , (6)

where α(η, ξ)andK(k, l) are angle and transform vectors, respectively, and

K · α =(kη + lξ). Noting the convolution structure of (4), the latter readily

transforms to

J =



¯σ(K

) − σ



ψ(k, l) , (7)

where K

= K ·K. Here and in the ensuing, appropriate behaviour of ψ and

its derivatives is assumed in order to justify the use of integral transforms.

We further ﬁnd it useful to express the Fourier transform of the diﬀerential

cross section ¯σ(K

) as a Hankel transform, namely

¯σ(K



∞

dλ λJ

(Kλ)ˆσ

(λ

) , (8)

where J

(·) is the zeroth order Bessel function of the ﬁrst kind. Proceeding,

the inﬁnite series representation of J

is used in (8) to express ¯σ as an ex-

pansion in K

and the result inserted into (7). We next take a formal inverse

Fourier transform of this equation to get, after some considerable algebra,

the desired diﬀerential representation of the collision integral

J[ψ]=

∞



n=1

ψ(η, ξ)=a

Lψ + a

ψ + O(a

) . (9)

448 A.K. Prinja and B.C. Franke

In the above expression, the a

are positive numerical coeﬃcients, L is the

2D planar Laplacian deﬁned by

L≡

∂

∂η

∂

∂ξ

, (10)

and we have introduced momentum transfer moments deﬁned by

=2π



−1

(1 − µ

)

(µ

) dµ

−n

2π



∞

dλ λ

2n+1

ˆσ

(λ

) . (11)

We note in passing that (9), with L replaced by the Laplacian on the unit

sphere, is related, but not identical, to the higher order Fokker-Planck expan-

sion introduced by Pomraning [GCP96] and subsequently used by Leakeas

and Larsen [LL01] to develop a generalized Fokker-Planck approximation for

the scattering integral. If scattering is suﬃciently forward peaked, the σ

will form a rapidly decreasing sequence and truncation of the expansion in

(9) is suggested. It is especially interesting to consider the approximation to

the collision integral that results from retaining only the ﬁrst term in this

sequence, namely

J[ψ] ≈



∂

∂η

∂

∂ξ



, (12)

where σ

≡ σ

is the familiar transport cross section. If, additionally, a thin

target is assumed, throughout which the angular distribution remains nearly

collimated, the resulting transport equation may be simpliﬁed to read

∂ψ

∂z

+ η

∂ψ

∂x

+ ξ

∂ψ

∂y



∂

∂η

∂

∂ξ



, (13)

with boundary condition

ψ(x, y, 0,η,ξ)=δ(x)δ(y)δ(η)δ(ξ) . (14)

This is the celebrated Fermi model, originally derived on physical grounds in

the context of cosmic ray penetration of the atmosphere [RG41] and which

has the following closed form joint Gaussian solution

ψ(x, y, z, η, ξ)=

× exp



−



3(x

+ y

)

−

3(xη + yξ)

(η

+ ξ

)

!

. (15)

An energy dependent generalization of this result in the continuous slow-

ing down approximation forms the basis of Fermi-Eyges theory that is

widely used but particularly so in electron dose calculations in radiother-

apy [HMA81]. The simplicity of this solution is undoubtedly a very attractive