Гиматудинов Ш.К. (ред.) Справочное руководство по проектированию разработки и эксплуатации нефтяных месторождений. Добыча нефти

Подождите немного. Документ загружается.

Аналогично рассчитываются последующие значения /, а затем проводится

суммирование (см. последнюю строку табл. Ш.5).

На

рис. II 1.3 представлено расчетное распределение давления по длине

труб

(кривая /).

На

этом же рисунке приводится кривая 2. В этом

случае

расчет <р про-

изводился по II 1.8, а потери на трение определялись по А. П. Крылову

(комбинированная

формула).

Методика

Н. Н.

Константинова

Для пробковой структуры с цилиндрической формой пробок общий

градиент давления выражается суммой

P ,

, Рг у , ,, г; >ж w'r ,

где 7=<p/f — доля длины трубы, занятая пузырями снарядной формы;

— (

r V

f = I -j- j — доля сечения трубы, занятая пузырями; d

(d) — диаметр пу-

1,68

зыря

(трубы); >.

31 — коэффициент сопротивления для жидкой пере-

мычки

между

пузырями, определяемый по приближенной формуле, получен-

ной

по опытным данным для пароводяной смеси;

—(v-\-q)

/f — средняя

линейная

скорость движения жидкости в перемычке, равная скорости движе-

ния

смеси; Re

=№c<i/v«, — число Рейнольдса, определяемое по скорости сме-

0,316v°-

си,

диаметру

трубы

и вязкости жидкости »

; Х

= —о

г5ло

г5~ 12— —

ко

эффициент

сопротивления газа, определяемый по Блазиусу, где за скорость

принимается

относительная скорость и движения пузырей по отношению

жидкости в кольцевом слое

между

стенками

трубы

и пузырями, а за

диаметр принимается диаметр пузыря; v

— кинематическая вязкость газа;

(1 — У) — Я?

= = — относительная скорость движения пузырей по отно-

f (I — f)f

шению к жидкости в кольцевом слое

между

пузырем и стенками трубы.

В уравнении (111.41)

третье

и последнее слагаемые обычно очень малы

по

сравнению с общей суммой, поэтому

Fr-

0,845

0,155

Основываясь на опытных данных Берингера и Газлайна (кинематическая

вязкость жидкости достигала

107-10-'

/с), а также на собственных опыт-

ных данных с водовоздушной смесью, Н. Н. Константинов пришел к

выводу,

что дробь

(1—

/РЯ'ж

остается постоянной, равной ^5=0,055. Отсюда

коэффи-

циент

сопротивления трения о стенки

трубы

для кольцевого слоя жидкости

Скорость подъема пузыря в неподвижной жидкости (?=0) определяется

соотношением

=«l,04

V d.

Для расчета f H. H. Константинов предлагает эмпирическое соотношение

(1—/)

«8/Р=0,0181 Ga»-'/

где Оа

= -^——критерий Галилея.

Применение

этой формулы для определения J (при заданном критерии

Галилея) связано с трудоемкими расчетами, поэтому нами предлагается со-

отношение

0Л

* (111.43,

Результаты опытов показывают, что J не зависит от длины пузыря.

Если принять вязкость воды равной Ы0-

/с, то при с(=4,03 см и

d=7,59

Ga» соответственно равно

642-10*

4289-10*.

При этих значениях

Ga,

согласно (111.43), f равно

0,875

0,884.

Для кинематической вязкости

двести раз большей, чем для воды, J равно 0,815 и

0,827

(соответственно

для диаметров 4,03 см и 7,59 см).

Константинов

Н. Н. предлагает следующие соотношения для расчета

истинной

газонасыщенности:

(Ш

44)

где

"р7"~-

]

Поскольку к

зависит от ф (см.

111.44

111.45),

следует

определять

методом подбора. В нефтяных скважинах чаще всего

Ф/Р<7,

т. е. надо при-

менять (111.44), которое можно упростить, если учесть, что

Рг

К ^ г

Тогда

** z г—ш •

(

I1L46

)

_L-f

6(i

—о

л /

Оа

г V

Аналогичная зависимость используется Уоллисом, а именно:

где а и

—

коэффициенты,

зависящие от физических свойств смеси.

Для водовоздушной смеси

1,14 + 0,341 Fr~°-

Отсюда

следует,

что скорость подъема пузыря в неподвижной жидкости-

составляет 0,341 У gd (Дэвис и Тейлор теоретически установили

коэффи-

циент

перед радикалом равным

0,35).

Согласно (111.46), влияние Ga

на-

численное значение ф невелико. Так, если Ga

=0,26-10

(d=4,03 см, v=

=500-10-* м

/с), то f=0,802, а множитель перед радикалом станет равным

0,337.

Несмотря на значительное изменение вязкости, от нее ощутимо не

зависит относительная скорость газовых пробок.

ростом скорости смеси (что равносильно увеличению числа Фруда)

второе слагаемое в знаменателе

(111.46)

стремится к нулю, поэтому q>max=

=fp.

Если

учесть,

что f=0,815—0,884, то фтах^О.вбО. Множитель 0,85 боль-

ше на 2% по сравнению с рекомендацией Арманда.

В начальной точке

(<7=0,

P=l), как это

следует

из уравнения А. П. Кры-

лова, при определенном значении расхода газа (см. табл. III.3) общий гра-

диент давления достигает минимального значения. Если же исходить из.

соотношения

(111.41),

то этого не наблюдается.

Точность расчетов движения газожидкостной смеси во многом зависит

от правильности определения истинной газонасыщенности. Рекомендуемые

различными авторами соотношения для расчета истинной газонасыщенности

нередко в значительной степени отличаются

друг

от

друга.

Приведем резуль-

таты расчетов (9=0, Р=1) при пробковой

структуре

потока:

тг-

(по

Н. Н. Константинову), (1П.481

—о (по А. П. Крылову —Г. С. Лутошкину), (III.48')

' (Frgrf)

где

- —

, - - , ,

С,=

6,06(1

— j

0,25

0,0503 0,0620 0,0759

51В=?!::::

5:8§

8:3? 8:35

Из

приведенных данных

следует,

что, несмотря на значительное измене-

ние

Gam, истинная газонасыщенность (при неизменном Fr) практически не

зависит от диаметра.

Пример

4. На основе данных примера 3 рассчитать градиенты давле-

ния,

истинную газонасыщенность и распределение давления по длине колонны

труб.

Расчеты вести по

(111.42)

учесть,

что средняя вязкость нефти в ко-

лонне

НКТ составляет

6,64-10-'

/с.

Реиение.

Для

труб

диаметром 6,2 см и вязкости

6,64-Ю-

/с

Са

=53-10

. Согласно

(111.43)

f=0,863. <р и е рассчитываем по

(111.46)

(111.42).

Результаты расчетов следующие:

р,

МПа 1 2 3 5 7 9,7

3 0,817

0,667

0,533

0,318 0,160 0

0,656

0,508

0,389

0,218 0,104 0

0,370

0,494

0,614

0,795

0,921 1,038

dp/dl,

МПа/м . . .

0,00311 0,00411

0,00509

0,00650

0,00743

0,00820

/, м — 277 217 345 287 345

и — 277 494 839 1126 1471

Таким

образом расчетные величины L достаточно близки к глубинам за-

меров давления (см. рис. Ш.З).

Методика А. М. Пирвердяна, А. И. Гузик и др.

В основу теории положено уравнение

(Ш.З).

Массой газа и инерционным

слагаемым авторы пренебрегают. Кроме того, они считают что: а) при разви-

той турбулентности (что свойственно фонтанным и газлифтным скважинам)

гидравлические сопротивления не зависят от числа Re; б) величина истинной

газонасыщенности зависит от р и Fr

; в) в газе содержится большое коли-

чество метана, поэтому можно пренебречь поправками на сжимаемость;

г) потери напора на трение определяются соотношением А. А. Арманда и

Е. И. Невструевой; д) плотность жидкой фазы по мере подъема остается

неизменной.

В окончательном виде уравнение записывается следующим образом:

dp (

i - Ыё! ^

(111.49)

Используя экспериментальные графики А. А. Точигина

ф=/(р)

(при

фиксированном

значении параметры Фруда смеси) и решая уравнение

(111.49)

-численным методом, можно применить следующие эмпирические соотношения:

,1/2

At",

РТ

:"•

(III.50)

где q — объемный

расход

жидкости, м

/с; g — ускорение свободного падения,

м/с

; Г — газовый фактор, м

/м

; е — общие потери напора на единицу длины

трубы; р

—

устьевое

давление; Рб — давление у башмака колонны НКТ; А,

n, tii — эмпирические безразмерные коэффициенты.

Для максимального дебита: Л = 3,55; /i=l,59,

Ai=0,\07,

щ=—2,51; при

работе подъемника на оптимальном режиме: Л=0,96, га=1,27, Л

=0,027,

= — 3,16.

Эти формулы получены для

труб

диаметром 4,03 и 6,2 см и при условии,

что рг/рш =

0,0006.

Если при подъеме жидкости по колонне большое значение имеет коли-

чество выделившегося из нефти газа (по сравнению с поступающим свобод-

ным

газом к башмаку НКТ), то погрешность приведенных соотношений воз-

растает. Таким образом,

увеличением обводненности скважины сходимость

между расчетными

фактическими данными должна возрастать.

Сравнение

расчетных величин

промысловыми данными позволило авто-

рам сделать вывод

применимости

для

расчетов теории

А. А.

Арманда

Е.

Невструевой, полученной

для

«коротких» колонн

труб

при

Р^0,9.

Методика

Е. В.

Шербестова

и Е. Г.

Леонова

Е.

В.

Шербестов

и Е. Г.

Леонов, основываясь

на

численном анализе

ре-

шений

системы уравнений (уравнения движения, неразрывности, состояния)

С.

Г.

Телетова, рекомендуют приближенные выражения

для

расчета распреде-

ления

давления

(при

пробковой структуре потока)

по

высоте скважины,

ког-

да ведется бурение

применением аэрированной жидкости. Авторы указы-

вают,

что

предлагаемые формулы

могут

быть использованы

и для

решения

задач, связанных

фонтанной

газлифтной эксплуатацией скважин.

Рекомендуемые соотношения записываются

следующем виде:

^•"

nBl

" ^ • (Ш.51)

при

(Fr

<3,72),

аВ -

10' f B\

+Ро

(IH.52)

Р^+Ро

—

при

(Fr

>3,72),

' ср

где

k =

2,3/>„

— j~,

ср

(г„)—коэффициент сжимаемости газа

при

сред-

них (нормальных) условиях; Г

р(Го)—средняя (нормальная) температура^

К;

a=vo/q

—

приведенное газовое число;

—

объемный расход свободного

газа

при р

р и Г

ср

приведенный

нормальным условиям,

/с; q —

объем-

ный

расход жидкости

при

средних условиях,

/с;

/1=1+0,811

5=0,19+0,0

Т1=(ц

/?)(рго/р

)

—

плотность свободного газа

при

нормальных условиях, кг/м

;

—

плот-

ность жидкой фазы

при

средних условиях; ,4i=n-f-T)-|-rt

Ci; Bi=2Cin

O,185<7

—

внутренний диаметр трубы,

м; pi —

давление

нижнем сечении трубы

(Pi^Pnac),

МПа;

р' —

давление

трубе,

где

=3,72;

—

давление

верх-

нем

сечении трубы,

МПа; U —

длина трубы,

м, где

p'^p^pi,

—

длина

трубы,

м, где

Рг^р<р'.

Применение

указанных формул ограничивается максимальным дебитом

/сут

(по

жидкости)

для

труб

диаметром

4,03 см. Для

других

диаметров

(5,03;

6,2; 7,59 см)

—121,

203, 337

/сут

соответственно. Отношение

не

должнв быть более

150

/м

(для

водо-воздушной смеси). Применительно-

газонефтяным смесям максимальный газовый фактор составляет

0,15рж

(р

кг/м

При

интегрировании были сделаны следующие допущения:

1) инерционным членам

уравнении движения принебрегли, поскольку

он

по

сравнению

другими слагаемыми очень

мал;

2) температура, коэффициент сжимаемости газа

г,

объемный расход

жидкости

по

всей длине

труб

остаются неизменными;

(v+q)

10000

WOO

3) в широком диапазоне измене-

ния

истинной газонасыщенности от

коэффициента

гидравлического со-

противления А, существенно не зави-

сит результат определения давления,

он может быть принят равным

4) при движении смеси

отсут-

ствуют

фазовые превращения;

5) структура смеси пробковая,

а истинная газонасыщенность опи-

сывается соотношением, рекомендо

ванным

В. А. Мамаевым, Г. Э. Оди-

шария

и др.:

2 3 ;,МПа

Рис.

III.4.

Зависимость между сум-

марным объемным расходом смеси

давлением

2,2

=-?

(Fr

<3,72);

(Fr

Ss3,72).

Приведенные формулы не учитывают физических свойств смеси и

могут

быть использованы только применительно к смесям, которые по своим свой-

ствам близки к воздуховодяным (800<рж<П00 кг/м

;

1,0<р

<50

кг/м

; 1<|ц

<20 мПа-с;

i|x

>10-

мПа-с).

Если Fr

=3,72, то

v+q=4,74d**.

(III.53)

Суммарный расход смеси, найденный по формуле (111.53), следующий:

d, см 4,03 5,03 6,20 7,59

(v + q),

м'/сут

134 232 392 650

Поскольку в нефтяных скважинах по мере подъема смеси газ выделя-

ется из нефти, расчеты надо вести по осредненным t>o, q; Рж-

Осреднение целесообразно проводить следующим образом. Задаваясь не-

сколькими

произвольными значениями давления, рассчитывать Vo, q, р

строить графики

t>o=/(p);

q=f(p);

Рж=Др).

На

основе этих графиков рассчитывать среднеиитегральные величины

рассматриваемых переменных в интервалах изменения давления

pi—р

—Р2'

Если Р1>ряас, то для нижнего интервала осреднения проводят при

изменении

давления от рнао до р

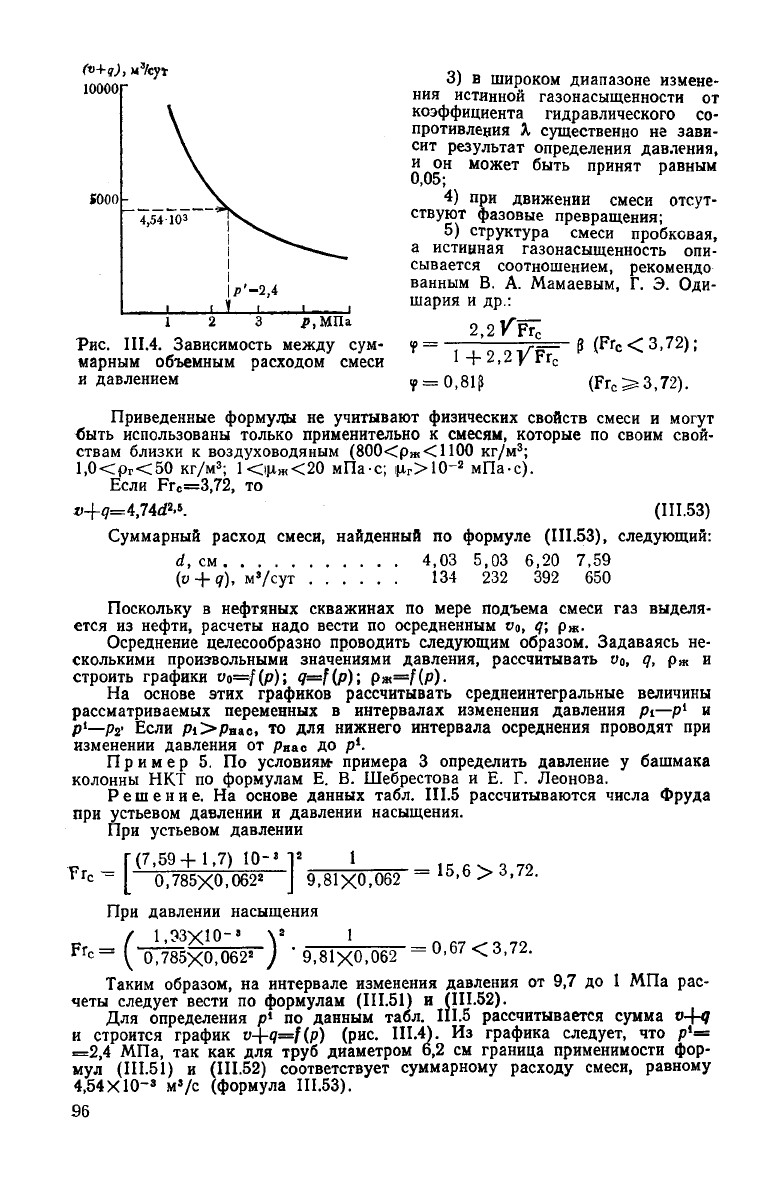
Пример

5. По условиям- примера 3 определить давление у башмака

колонны

НКТ по формулам Е. В. Шебрестова и Е. Г. Леонова.

Решение.

На основе данных табл.

III.5

рассчитываются числа Фруда

при

устьевом давлении и давлении насыщения.

При

устьевом давлении

Тг,

_ Г (7,59+1,7) 10-" I

~ [

0,785X0,062

9,81X0,062

15,6 > 3,72.

При

давлении насыщения

1,93ХЮ-'

)

0,67<3,72.

0,785X0,06

)

'9,81X0,062

Таким

образом, на интервале изменения давления от 9,7 до 1 МПа рас-

четы

следует

вести по формулам

(111.51)

и (111.52).

Для определения р

по данным табл. Ш.5 рассчитывается сумма v+q

строится график

v-\-q=f(p)

(рис. Ш.4). Из графика

следует,

что p

=2,4

МПа, так как для

труб

диаметром 6,2 см граница применимости фор-

мул

(111.51)

(111.52)

соответствует суммарному

расходу

смеси, равному

4,54X10-»

м»/с (формула

111.53).

При

решении примера 3 было установлено, что

(^=845—

5,6р,

[50,6 — 5,28 (р — 0,1)]/-122С00

°»~"

86400X844

Поскольку

и и

линейно зависят от давления, при определении сред-

них

значений рассматриваемых величин можно исходить из среднеарифме-

тических давлений на каждом интервале изменения давления. Для нижнего

интервала (от 9,7 до 2,4 МПа) среднее давление составляет 5,9 МПа, по-

этому

845 —

5,6-5,9

= 812 кг/м

[50,6 — 5,28(5,9—

0,1)]-122000

"•-

86400-844

=33.5.10- м'/с

Аналогично ведется расчет и для верхнего интервала давлений, где сред-

нее

составляет 0,5(2,4+1,0) = 1,7 МПа. Тогда р

= 835 кг/м

, о

=70,ЗХ

Х10-

м'/с

Секундный

объемный расход жидкой фазы определяется следующим со-

отношением

(см. пример 3):

122000+

992,2

(/7—0,1)

= 86400

Рж

Для нижнего интервала ^=0,00182 м

/с.

Для верхнего интервала <7=О,ОО171

з/

Основываясь

на соотношениях (111.51) и (111.52), рассчитываем длину

интервалов.

Для верхнего интервала при

z^szzo

*=2,3

-Цр=

0,232,

а = у„/9=70,3-10-'/1,71-10-

= 41,1,

п-=\

+0,185<7/d

= 1 +- 0,1850,00171/0,062

1,331,

1=К/?)(Рг,/Рж)

= (70,3-10-'/1,71-Ю-

) (1,3/835) =0,064.

А= 1+0,81-4 +

0,0051

(•>)+

0,81)<7»/rf

= 1 + 0,81

-0,064

(1.71-»)»

0,0051

(0,064 + 0,81) 0

062»

= 1>066

В= 0,19+

0,0041

[1+1] (У; +

0,81)]<77^

0,19 +

0,0041

[1 +

0,064/(0,064

+ 0,81 )J(1,71-10

)

/0,Об2

0,204.

2,4—1+0,232-41,1 [ 1 —

,066

835-9,81-1,066

41,1-0,204

382,5 м.

°'

204

тже;

41,10,204

1,066

Аналогичные расчеты проводятся по формуле (111.51) для нижнего ин-

тервала, где давление изменяется от 9,7 до 2,4 МПа:

в==

18,407; я=

1,352;

ij = 0,0295; С, =

1,07-Ю-

;

Л,=

1,414;

В, = 0,0285; /, =

1100,2

Таким

образом, на глубине 383+1100=1483 м давление равно 9,7 МПа

{см. рис.

III.4).

Замеренное давление на глубине 1600 м составляет 10,89 МПа.

Расчетное давление на этой глубине 9,7+0,01(1600—1483)0,790=10,1 МПа,

т. е. меньше замеренного на 0,27 МПа, что составляет 2,5% (по сравнению

результатами замеров).

Методика Р. И. Медведского, Ф. Г. Аржанова и др.

В основу теории положено уравнение (III.3) без

учета

инерционного чле-

на

и принято, что

ф=ар,

тогда

где р = Pg (а + Ьд) — плотность смеси, рассчитанная по истинной газонасы-

щениости,

кг/м

; р

= (1—Р) р

+ ?рг =

ч/^ — плотность смеси, рассчитанная

по

расходной газонасыщенности, кг/м

; mo=p

o-H?«Pro — масса газожидкоетт

ной

смеси, приходящаяся на 1 м

дегазированной нефти (приведенной к нор-

мальным условиям р

и Го), кг/м

; р

о (pro) — плотность нефти (газа)

при

нормальных условиях, кг/м

; 7?о — газовый фактор, м

/м

;

ft=(Ro—f)X

Х&г+Ьн

— объемный коэффициент газожидкостной смеси; г — количество

растворенного газа, приходящееся на единицу объема дегазированной нефти

Ра

при

заданных р и Т, м

/м

; 6

= ——

•

-у— — объемный коэффициент сво-

бодного газа при давлении р и температуре Т; Ь

— объемный коэффициент

нефти;

г — коэффициент сжимаемости газа, 6=(1—a)p

<,/b

;

dp \ ц

= l Fr

86400

условное число Фруда, рассчитанное по линейной скорости движения (qn=f)

, к

68 ••*-

дегазированности нефти; Л =0,11 I —j- = н^~ I —коэффициент ги-

дравлического трения газожидкостного потока, рассчитывается по обобщенной

формуле А. Д.

Альтшуля;

H =

—2 — —условное число Рейнольдса,

fH-н

рассчитанное по приведенной скорости жидкости и вязкости нефти; k

—

эквивалентная

равномерно зернистая шероховатость.

Величина k

в значительной мере зависит от состояния

труб.

Для новых

стальных

труб

=0,01—0,02

мм. С течением времени численное значение

возрастает в несколько раз.

Для высокодебитных скважин рекомендуется исходить из соотношения

Арманда (а=0,833). После подстановки выражения для потерь напора на

трение и р в (Ш.54)

1155

)

где pi и Pi — давления на концах

трубы

длиною /; / определяется численным

интегрированием правой части приведенного соотношения.

Для наклонных скважин вместо Fro

следует

использовать Fro/cos a

(а

—

угол

между

осью скважины и вертикалью). Под / понимается разность

отметок сечений, где давления р, и рг- Если

угол

наклона по высоте — ве-

личина

переменная (что характерно для реальных условий), то всю глубину

скважины

необходимо разделить на несколько участков и для каждого

участ-

ка

принимать а постоянной.

Если

(111.55)

принять а=1 (следовательно, Ь=0), то получится урав-

нение

Поэтмана и Карпентера.

Авторы

считают, что коэффициенты о и & в (III.54) зависят от числа

Фруда смеси

={v-^q)

/(2f

gd).

Зависимость указанных коэффициентов от числа Fr

устанавливают по

результатам обработки промысловых данных (распределение давления по

длине колонны НКТ, свойств нефти и газа).

Используя

данные поинтервальных замеров давления, на основании

(111.55)

можно определить коэффициенты а и Ь. Для этого рассматриваемое

соотношение

следует

представить в следующем виде:

(III.56)

Если

коэффициент X считать по длине

труб

неизменным, то, пользуясь

соотношением

(111.56), можно определить его. Для этого вычитаемое надо

перенести в

левую

часть уравнения.

При

расчетах 6 надо исходить из среднеарифметического давления на

интервале А/. Коэффициенты а и b определяются методом средних или на-

именьших квадратов. Накопленный статистический материал позволит обоб-

щить

обширные промысловые данные и ввести коррективы в численные

значения

изучаемых коэффициентов.

Сравнение

расчетных кривых распределения давления по длине

труб

с ре-

зультатами промысловых замеров показало, что при Fr

<l требуемая точ-

ность

не обеспечивается.

Методика Поэттмана и Карпентера

Поэттман

и Карпентер, основываясь на уравнении Бернулли и прене-

брегая изменением кинетической энергии потока, рассматривают движение

газожидкостной смеси как течение однородной среды

где &h — расстояние

между

двумя сечениями трубы; pj, pi — давление в

верх-

нем

и нижнем сечениях трубы; V

— удельный объем смеси; V

=l/p

; p

—

плотность смеси при давлении р и температуре Т;

t»

— средняя линейная

скорость движения смеси на участке длиною ДА; d — диаметр трубы; fo—

коэффициент

гидравлических сопротивлений.

Изменение

общего градиента давления за счет относительной скорости

трения учитывается вторым слагаемым в знаменателе.

Так

как линейная скорость смеси по длине колонны НКТ изменяется,

то правильно вместо

(111.57)

написать выражение

Р*

h определяется численным интегрированием; р

(в кг/м

) и w

(в м/с) опре-

деляют при помощи соотношений

рс=

+ v

B +

=ТГ

86400

где М

—суммарная масса нефти (М

), воды (Af

) и газа (М

), добывае-

мых в сутки, кг/сут; V

— общий расход смеси,

/сут;

, V

— расходы

соответственно нефти, воды и газа, приведенные к давлению р и темпера-

туре

Т,

м'/сут.

В отличие от ряда

других

исследований здесь не учитывается зависи-

мость плотности смеси от относительной скорости.

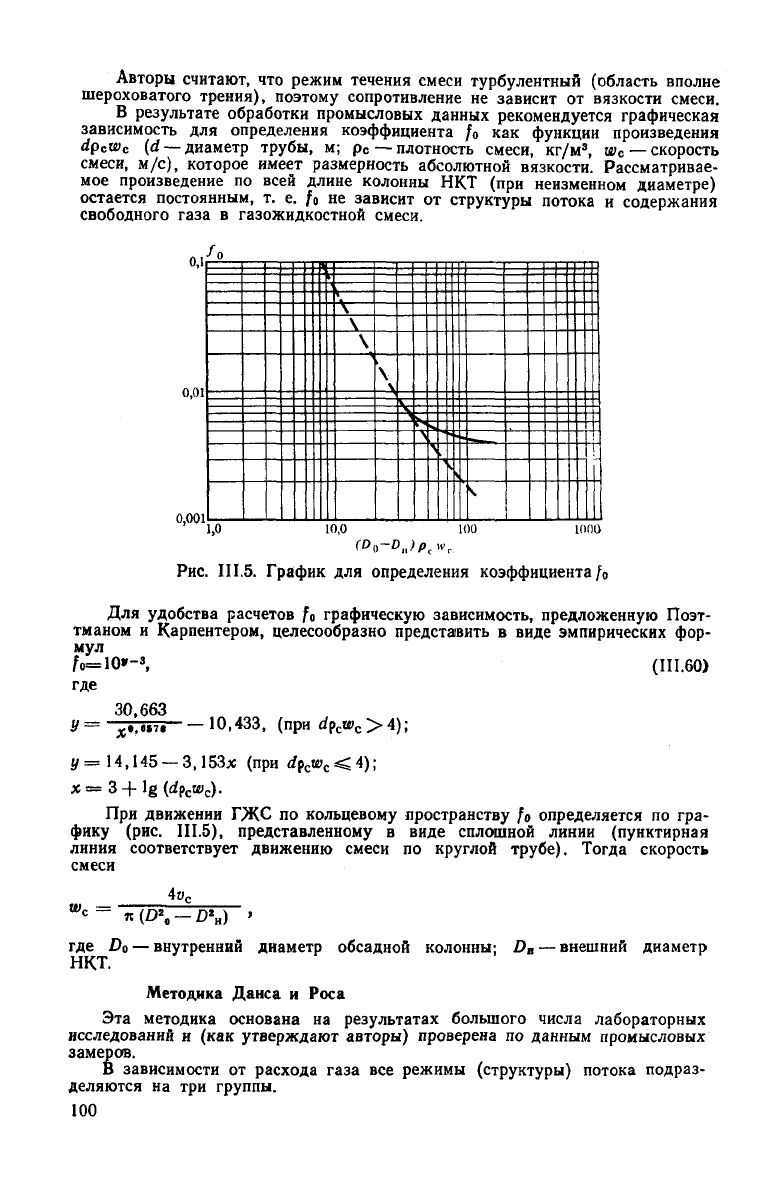
Авторы

считают, что режим течения смеси турбулентный (область вполне

шероховатого трения), поэтому сопротивление не зависит от вязкости смеси.

результате

обработки промысловых данных рекомендуется графическая

зависимость для определения коэффициента /о как функции произведения

(d — диаметр трубы, м; р

— плотность смеси, кг/м

, w

— скорость

смеси,

м/с), которое имеет размерность абсолютной вязкости. Рассматривае-

мое произведение по всей длине колонны НКТ (при неизменном диаметре)

остается постоянным, т. е. /

не зависит от структуры потока и содержания

свободного газа в газожидкостной смеси.

0,1

0,01

0,001

•

V «

1,0

10,0 100

10(10

Рис.

II 1.5. График для определения коэффициента/

Для

удобства

расчетов fo графическую зависимость, предложенную Поэт-

тманом и Карпентером, целесообразно представить в виде эмпирических фор-

мул

/о=1О»-

(111.60)

где

30,663

-10,433, (при rfp

t»

>4);

i/=

14,145

—

3,153х

(при rfp

<4);

x=3

lg(dp

При

движении ГЖС по кольцевому пространству f

определяется по гра-

фику

(рис.

III.5),

представленному в виде сплошной линии (пунктирная

линия

соответствует

движению смеси по круглой трубе). Тогда скорость

смеси

где Do — внутренний диаметр обсадной колонны; D

— внешний диаметр

НКТ.

Методика Данса и Роса

Эта методика основана на

результатах

большого числа лабораторных

исследований и (как

утверждают

авторы) проверена по данным промысловых

замеров.

В зависимости от расхода газа все режимы (структуры) потока подраз-

деляются на три группы.

100