Gibilisco S. Teach Yourself Electricity and Electronics

Подождите немного. Документ загружается.

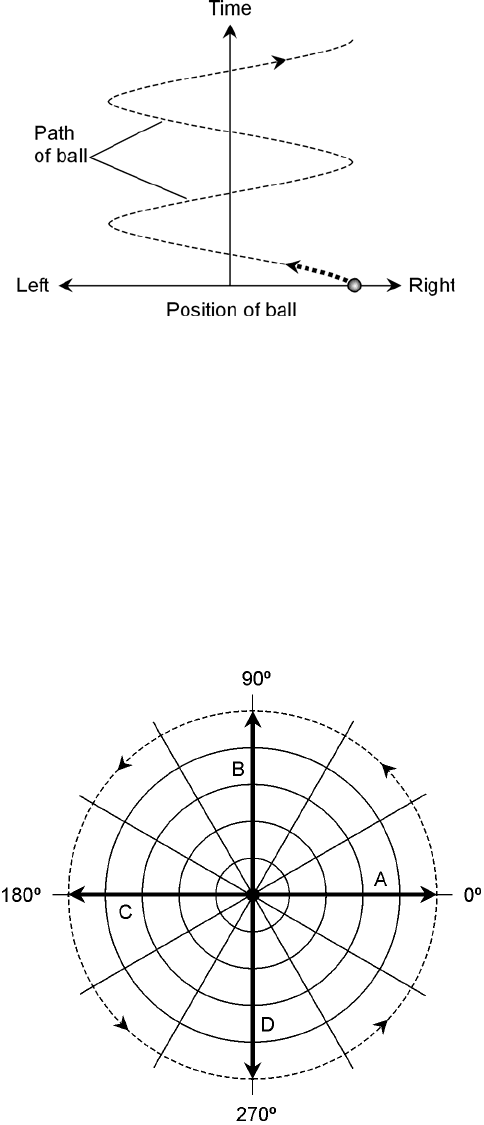
Figure 12-5 shows the way a rotating vector can be used to represent a sine wave. A vector is a

quantity with two independent properties, called magnitude (or amplitude) and direction. At A, the

vector points east, and this is assigned the value of 0°, where the wave amplitude is zero and is in-

creasing positively. At B, the vector points north; this is the 90° instant, where the wave has attained

its maximum positive amplitude. At C, the vector points west. This is 180°, the instant where the

wave has gone back to zero amplitude and is getting more negative. At D, the wave points south.

This is 270°, and it represents the maximum negative amplitude. When a full circle (360°) has been

completed, the vector once again points east.

The four points in Fig. 12-5 are shown on a sine wave graph in Fig. 12-6. Think of the vector as

revolving counterclockwise at a rate that corresponds to one revolution per cycle of the wave. If the

wave has a frequency of 1 Hz, the vector goes around at a rate of 1 rps. If the wave has a frequency of

12-4 Position of ball

(horizontal axis) as

seen from the side,

graphed as a function

of time (vertical axis).

12-5 Rotating-vector

representation of a sine

wave. At A, at the start

of the cycle; at B, one-

fourth of the way

through the cycle; at

C, halfway through

the cycle; at D, three-

fourths of the way

through the cycle.

Circles and Vectors 191

192 Phase

100 Hz, the speed of the vector is 100 rps, or a revolution every 0.01 s. If the wave is 1 MHz, then

the speed of the vector is 1 million rps (10

rps), and it goes once around every 0.000001 s (10

−6

s).

The peak amplitude of a pure ac sine wave corresponds to the length of its vector. In Fig. 12-5,

time is shown by the angle counterclockwise from due east. Amplitude is independent of time. The

vector length never changes, but its direction does.

Expressions of Phase Difference

The phase difference, also called the phase angle, between two waves can have meaning only when

those two waves have identical frequencies. If the frequencies differ, even by just a little bit, the rel-

ative phase constantly changes, and it’s impossible to specify a value for it. In the following discus-

sions of phase angle, let’s assume that the two waves always have identical frequencies.

Phase Coincidence

Phase coincidence means that two waves begin at exactly the same moment. They are “lined up.”

This is shown in Fig. 12-7 for two waves having different amplitudes. The phase difference in this

12-6 The four points for the

vector model of Fig.

12-5, shown in the

standard amplitude-

versus-time graphical

manner.

12-7 Two sine waves in

phase coincidence.

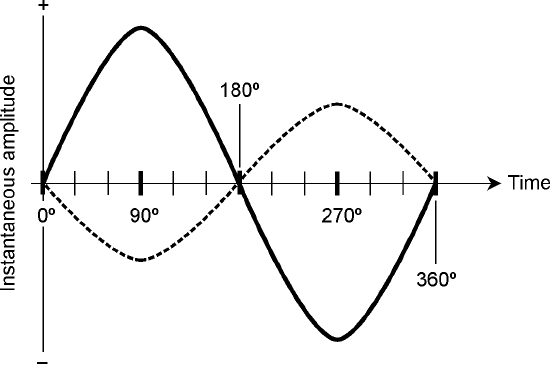
case is 0°. You could say it’s some whole-number multiple of 360°, too—but engineers and techni-

cians rarely speak of any phase angle of less than 0° or more than 360°.

If two sine waves are in phase coincidence, and if neither wave has dc superimposed, then the

resultant is a sine wave with positive or negative peak amplitudes equal to the sum of the positive

and negative peak amplitudes of the composite waves. The phase of the resultant is the same as that

of the composite waves.

Phase Opposition

When two sine waves begin exactly

⁄2 cycle, or 180°, apart, they are said to be in phase opposition.

This is illustrated by the drawing of Fig. 12-8. In this situation, engineers sometimes say that the

waves are out of phase, although this expression is a little nebulous because it could be taken to mean

some phase difference other than 180°.

If two sine waves have the same amplitudes and are in phase opposition, they cancel each other

out. This is because the instantaneous amplitudes of the two waves are equal and opposite at every

moment in time.

If two sine waves are in phase opposition, and if neither wave has dc superimposed, then the re-

sultant is a sine wave with positive or negative peak amplitudes equal to the difference between the

positive and negative peak amplitudes of the composite waves. The phase of the resultant is the same

as the phase of the stronger of the two composite waves.

Any sine wave without superimposed dc has the unique property that, if its phase is shifted by

180°, the resultant wave is the same as turning the original wave upside down. Not all waveforms

have this property. Perfect square waves do, but some rectangular and sawtooth waves don’t, and ir-

regular waveforms almost never do.

Intermediate Phase Differences

Two sine waves can differ in phase by any amount from 0° (phase coincidence), through 90° ( phase

quadrature, meaning a difference a quarter of a cycle), 180° (phase opposition), 270° (phase quad-

rature again), to 360° (phase coincidence again).

12-8 Two sine waves in

phase opposition.

Expressions of Phase Difference 193

194 Phase

Leading Phase

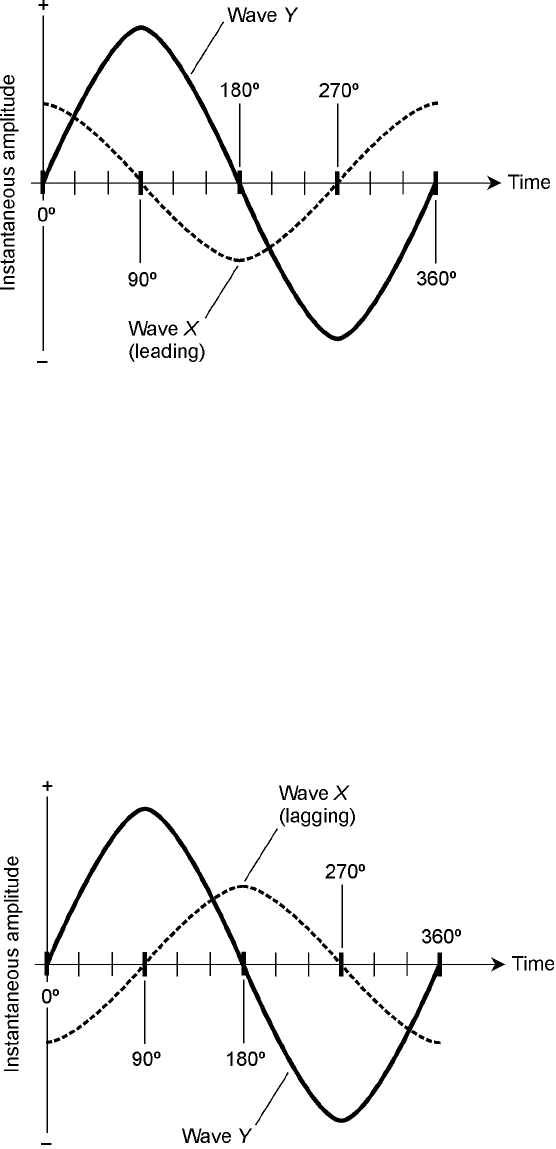
Imagine two sine waves, called wave X and wave Y, with identical frequency. If wave X begins a

fraction of a cycle earlier than wave Y, then wave X is said to be leading wave Y in phase. For this

to be true, X must begin its cycle less than 180° before Y. Figure 12-9 shows wave X leading wave

Y by 90°.

Note that if wave X (the dashed line in Fig. 12-9) is leading wave Y (the solid line), then wave

X is displaced to the left of wave Y. In a time-domain graph or display, displacement to the left rep-

resents earlier moments in time, and displacement to the right represents later moments in time.

Lagging Phase

Suppose that some sine wave X begins its cycle more than 180°, but less than 360°, ahead of wave

Y. In this situation, it is easier to imagine that wave X starts its cycle later than wave Y, by some value

between 0° and 180°. Then wave X is not leading, but lagging, wave Y. Figure 12-10 shows wave X

lagging wave Y by 90°.

12-10 Wave X lags wave Y

by 90° of phase

(

⁄4 of a cycle).

12-9 Wave X leads wave Y

by 90° of phase (

⁄4 of

a cycle).

Vector Diagrams of Phase Difference

The vector renditions of sine waves, such as are shown in Fig. 12-5, are well suited to showing phase

relationships.

If a sine wave X leads a sine wave Y by some number of degrees, then the two waves can be

drawn as vectors, with vector X being that number of angular degrees counterclockwise from vector

Y. If a sine wave X lags a sine wave Y by some number of degrees, then X appears to point in a di-

rection that is clockwise from Y by that number of angular degrees. If two waves are in phase coinci-

dence, then their vectors point in exactly the same direction. If two waves are in phase opposition,

then their vectors point in exactly opposite directions.

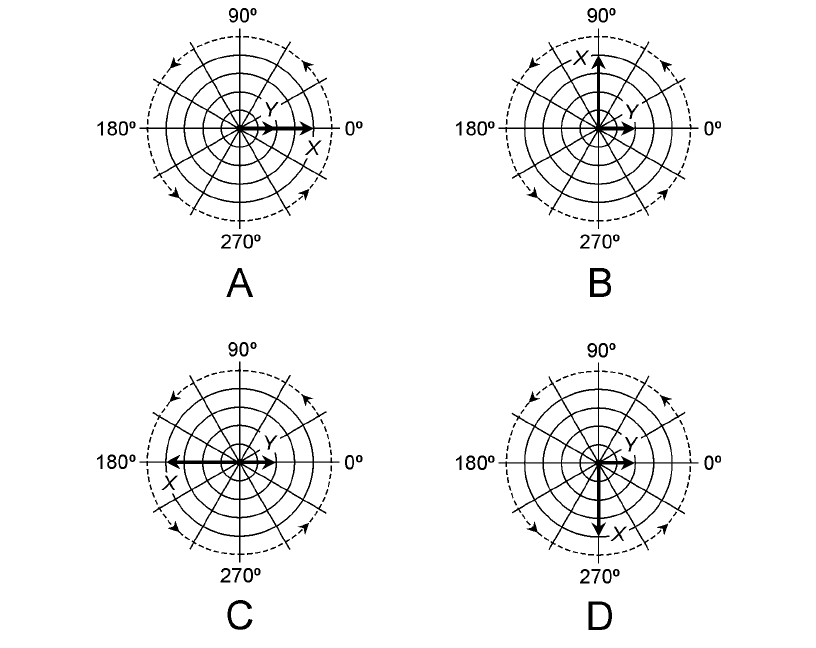
The drawings of Fig. 12-11 show four phase relationships between two sine waves X and Y. At

A, X is in phase with Y. At B, X leads Y by 90°. At C, X and Y are 180° apart in phase. At D, X lags

Y by 90°. In all of these examples, think of the vectors rotating counterclockwise as time passes, but

always maintaining the same angle with respect to each other, and always staying at the same

lengths. If the frequency in hertz is f, then the pair of vectors rotates together, counterclockwise, at

an angular speed of f, expressed in complete 360° revolutions per second.

12-11 Vector representations of phase difference. At A, waves X and Y are in

phase. At B, X leads Y by 90°. At C, X and Y are 180° out of phase. At

D, X lags Y by 90°. Time is represented by counterclockwise motion of

both vectors at a constant angular speed.

Vector Diagrams of Phase Difference 195

Quiz

Refer to the text in this chapter if necessary. A good score is 18 correct. Answers are in the back of

the book.

1. Which of the following is not a general characteristic of an ac wave?

(a) The wave shape is identical for each cycle.

(b) The polarity reverses periodically.

(d) There is a definite frequency.

2. All sine waves

(a) have similar general appearance.

(b) have instantaneous rise and fall times.

(d) rise instantly, but decay slowly.

3. The derivative of a sine wave

(a) is shifted in phase by

⁄2 cycle from the sine wave.

(b) is the rate of change in the instantaneous value.

(d) rises instantly, but decays slowly.

4. A phase difference of 180° in the circular motion model of a sine wave represents

(a)

⁄4 revolution.

(b)

⁄2 revolution.

(d) two full revolutions.

5. You can add or subtract a certain number of degrees of phase to or from a wave, and end up

with exactly the same wave again. This number is

(a) 90, or any whole-number multiple of it.

(b) 180, or any whole-number multiple of it.

(d) 360, or any whole-number multiple of it.

6. You can add or subtract a certain number of degrees of phase to or from a sine wave, and end

up with an inverted (upside-down) representation of the original. This number is

(a) 90, or any odd whole-number multiple of it.

(b) 180, or any odd whole-number multiple of it.

(d) 360, or any odd whole-number multiple of it.

196 Phase

7. Suppose a wave has a frequency of 300 kHz. How long does one complete cycle take?

(a) 1.300 s

(b) 0.00333 s

(d) 3.33 × 10

−6

8. If a wave has a frequency of 440 Hz, how long does it take for 10° of a cycle to occur?

(a) 0.00273 s

(b) 0.000273 s

(d) 0.00000631 s

9. Suppose two waves are in phase coincidence. One has peak values of ⫾3 V and the other has

peak values of ⫾5 V. The resultant has voltages of

(a) ⫾8 V pk, in phase with the composites.

(b) ⫾2 V pk, in phase with the composites.

(d) ⫾2 V pk, in phase opposition with respect to the composites.

10. As shown on a graph, shifting the phase of an ac sine wave by 90° is the same thing as

(a) moving it to the right or left by a full cycle.

(b) moving it to the right or left by

⁄4 cycle.

(d) leaving it alone.

11. Two pure sine waves that differ in phase by 180° can be considered to

(a) be offset by two full cycles.

(b) be in phase opposition.

⁄4 cycle.

(d) have a frequency of

⁄2 cycle.

12. Suppose two sine waves are in phase opposition. Wave X has a peak amplitude of ⫾4 V and

wave Y has a peak amplitude of ⫾8 V. The resultant has voltages of

(a) ⫾4 V pk, in phase with the composites.

(b) ⫾4 V pk, out of phase with the composites.

(d) ⫾4 V pk, in phase with wave Y.

13. If wave X leads wave Y by 45°, then

(a) wave Y is

⁄4 cycle ahead of wave X.

(b) wave Y is

⁄4 cycle behind wave X.

⁄8 cycle behind wave X.

(d) wave Y is 1.16 cycle ahead of wave X.

Quiz 197

14. If wave X lags wave Y by

⁄3 cycle, then

(a) wave Y is 120° ahead of wave X.

(b) wave Y is 90° ahead of wave X.

(d) wave Y is 30° ahead of wave X.

15. Refer to Fig. 12-12. In this example,

(a) X lags Y by 45°.

(b) X leads Y by 45°.

(d) X leads Y by 135°.

16. Which of the drawings in Fig. 12-13 represents the situation of Fig. 12-12?

(a) Drawing A

(b) Drawing B

(d) Drawing D

17. In vector diagrams such as those of Fig. 12-13, the length of the vector represents

(a) the average amplitude of a sine wave.

(b) the frequency of a sine wave.

(d) the peak amplitude of a sine wave.

18. In vector diagrams such as those of Fig. 12-13, the angle between two vectors represents

(a) the average of the peak amplitudes of two sine waves.

(b) the frequency difference between two sine waves.

(d) the difference between the peak amplitudes of two sine waves.

198 Phase

12-12 Illustration for Quiz

Question 15.

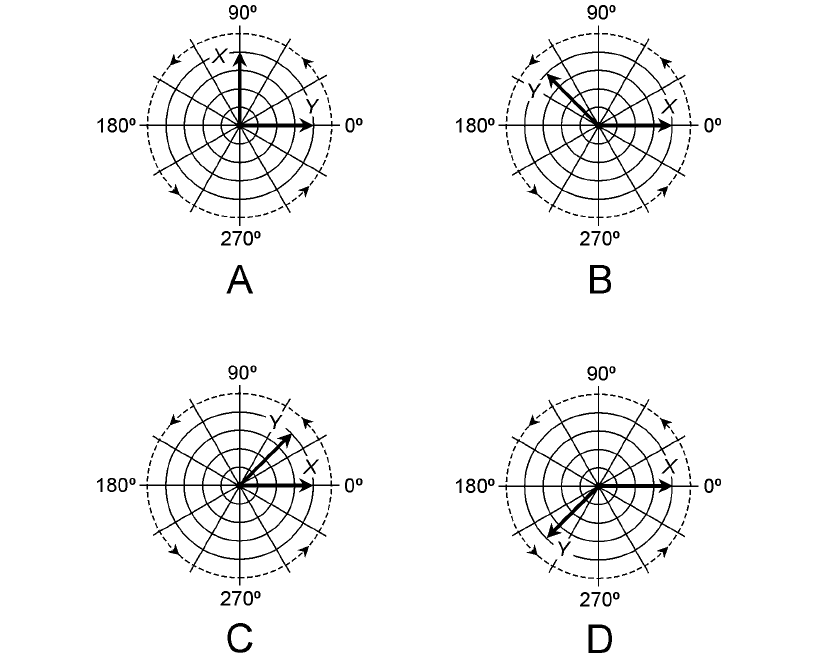
19. In vector diagrams such as those of Fig. 12-13, the distance from the center of the graph

represents

(a) average amplitude.

(b) frequency.

(d) peak amplitude.

20. In diagrams like those of Fig. 12-13, the progression of time is sometimes depicted as

(a) movement of a vector to the right.

(b) movement of a vector to the left.

(d) clockwise rotation of a vector.

12-13 Illustration for Quiz Questions 16 through 20.

Quiz 199

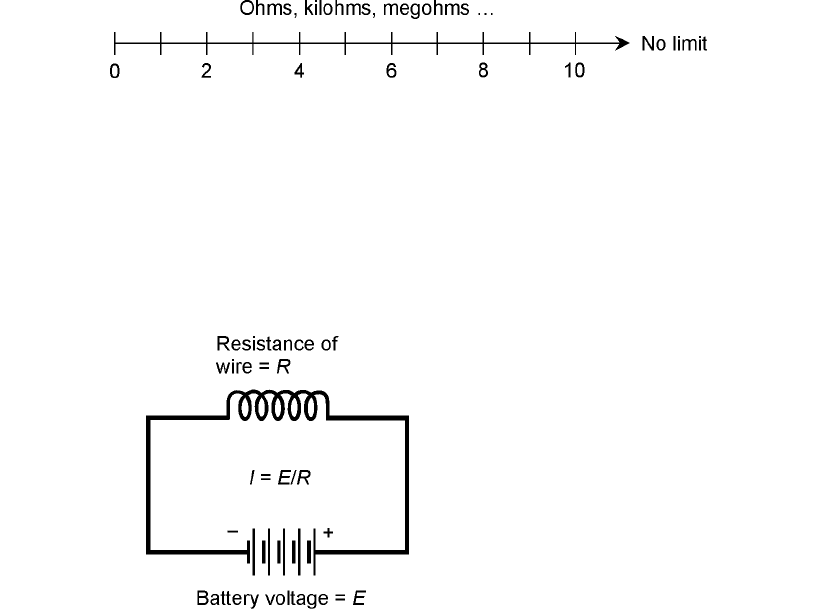
IN DC CIRCUITS, RESISTANCE CAN BE EXPRESSED AS A NUMBER RANGING FROM ZERO (REPRESENTING

a perfect conductor) to extremely large values. Physicists call resistance a scalar quantity, because it

can be expressed on a one-dimensional scale, as shown in Fig. 13-1.

200

CHAPTER

Inductive Reactance

13-1 Resistance can be represented as numerical values (corresponding to

ohms) along a half line or ray.

13-2 An inductor connected

across a source of dc.

Coils and Direct Current

Suppose you have some wire that conducts electricity very well. If you wind a length of the wire into

a coil and connect it to a source of dc (Fig. 13-2), the wire draws a large current. It doesn’t matter