George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

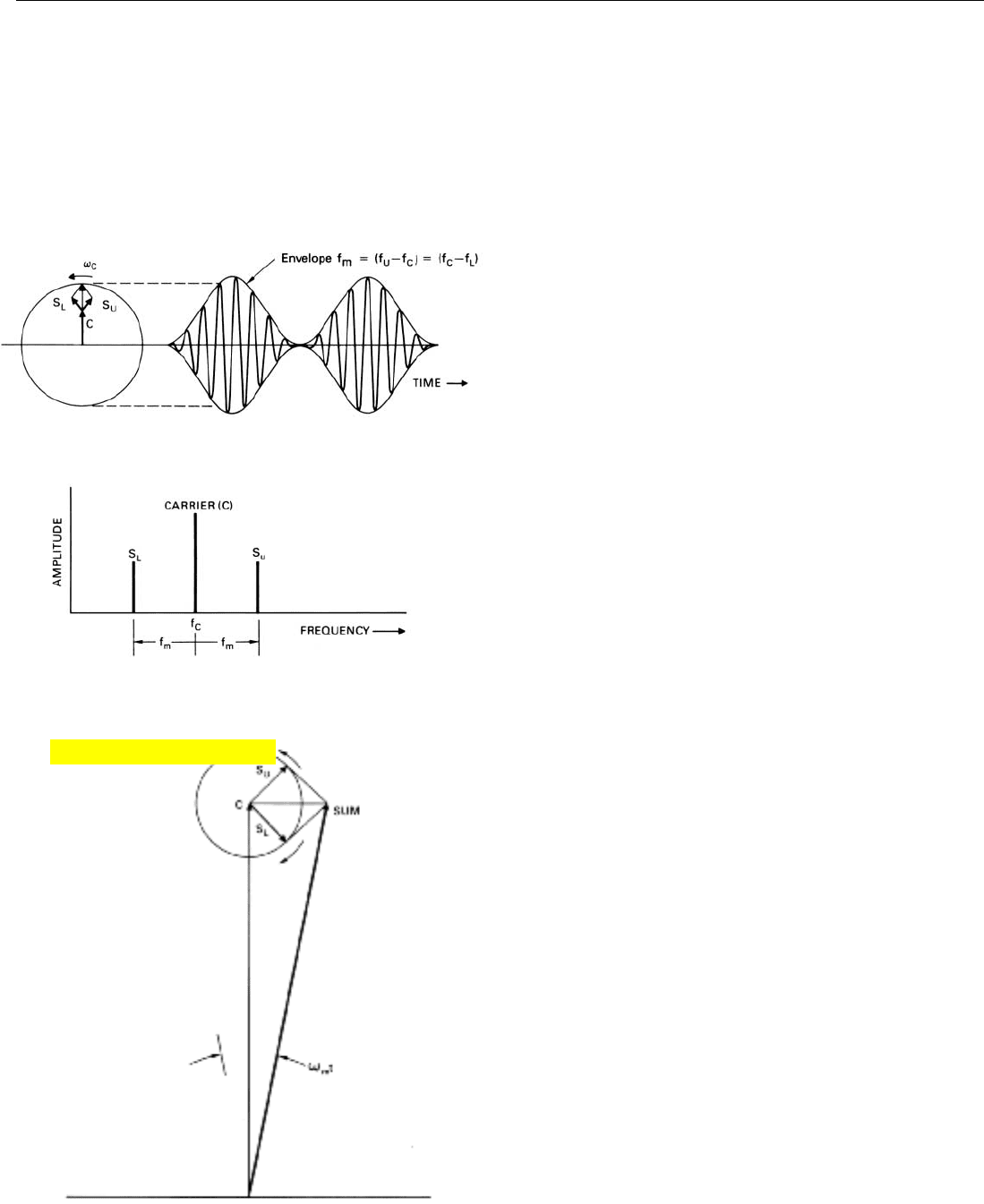
18. If amplitude of a carrier signal C is varied sinusoidally at rate,

, two new signals are produced, S

and S

19. Since the frequencies of S

and S

are f

hertz above and

below f

, they are called sidebands.

PART II Essential Groundwork

rotating phasors and the frequency of the “fixed” phasor.

All three phasors, of course, rotate in unison with that pha-

sor. But this rotation doesn’t show up in the diagram

because the imaginary strobe light which illuminates the

phasors flashes “on” only once in every cycle of that pha-

sor’s rotation.

In some instances amplitude modulation is actually pro-

duced by generating the signals represented by the counter-

rotating phasors separately and adding them to the signal

that is to be modulated. Generally, though, it is the other

way around. The signals represented by the counter-rotating

phasors are the inevitable result of amplitude modulation.

As is illustrated by the phasor diagram of Fig. 18 and

may be readily demonstrated with actual signals, whenever

the amplitude of a signal of a given frequency (f

) is modu-

lated at a lower frequency (f

), two new signals are invari-

ably produced. One of these, represented by the phasor S

in Fig. 18, has a frequency f

hertz above f

; the other, a

frequency f

hertz below it.

Since the frequencies of these signals lie on either side of

(Fig. 19), the signals are called sideband signals, or sim-

ply sidebands. Since the signal that is modulated carries the

modulation—i.e., the modulation is added to and subtracted

from the amplitude of this signal— it is called the carrier.

The light lines that join the crests of the modulated wave

in Fig. 18 delineate what is called the modulation envelope.

The frequency of the sidebands, you will notice, is the mod-

ulation frequency. The average separation of the sidebands

from the baseline is the amplitude of the carrier.

Sidebands are similarly produced when the phase or fre-

quency of a carrier signal is modulated. Only then, the

phase relationship of the sidebands to the carrier is different

(Fig. 20). If the percentage by which the phase or frequency

is varied is large, many sideband pairs separated by multi-

ples of the modulation frequency are created.

The generation of sidebands is an important considera-

tion in the design of virtually every radar. As will be

explained in detail in Chap. 9, for example, it is to avoid

interference from sidebands due to the random fluctuation

(noise modulation) of the output of the radar transmitter

that one generally must employ pulsed transmission when

the same antenna is used for both transmission and recep-

tion.

And, as will be explained in Chap. 23, it is the produc-

tion of sidebands by the pulsed modulation of the transmit-

ter that in some cases causes echoes from a target and a

ground patch to be passed by the same doppler filter even

though they have different doppler frequencies.

20. Frequency and phase modulation differ from amplitude modula-

tion in that the phase of the sideband signals is shifted by 90˚.

Click for high-quality image

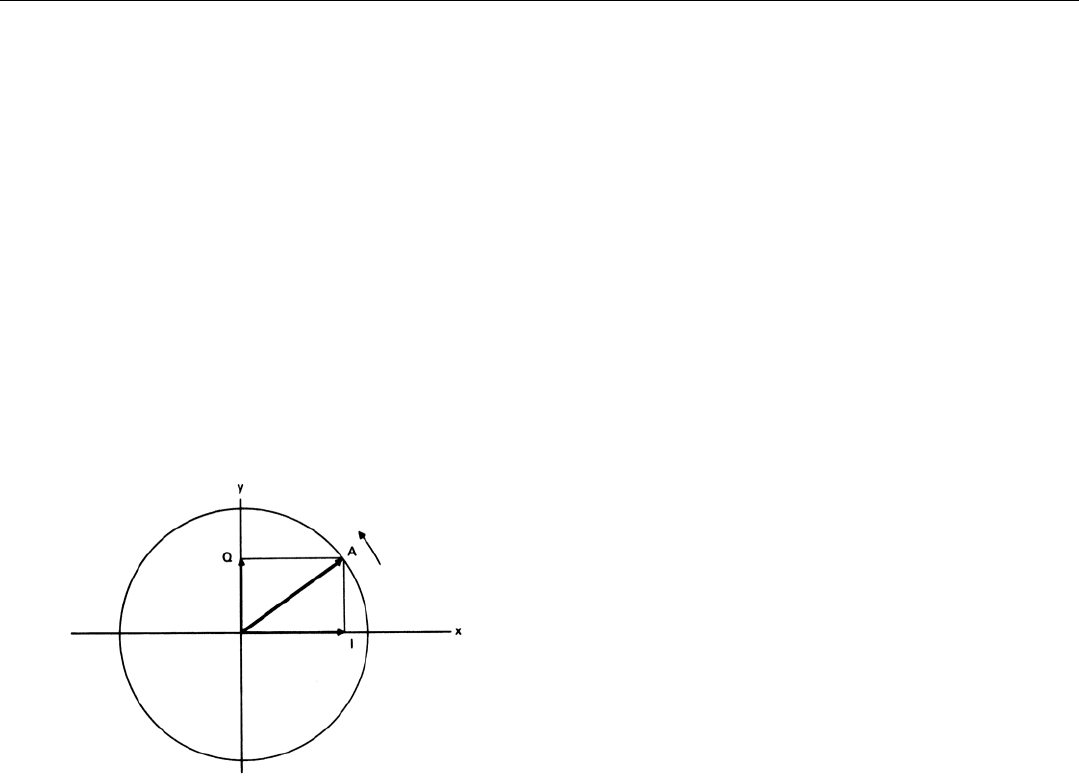
CHAPTER 5 Key to a Nonmathematical Understanding of Radar

Resolving Signals into I and Q Components

Sometimes it is advantageous to resolve a signal into two

components having the same frequency and peak ampli-

tude but differing in phase by 90˚. Since a cosine wave

reaches its positive peak 90˚ before a sine wave does, the

most convenient way of picturing the two components is as

a sine wave (A sin ωτ) and a cosine wave (A cos ωτ). By

convention, the cosine wave is called the in-phase or I com-

ponent.

Since 90˚ is a quarter of a circle, the sine wave is

called the quadrature or Q component.

If the signal is represented by a phasor, the instantaneous

amplitude of the I component can be found simply by pro-

jecting the phasor onto the horizontal (x) axis. The instan-

taneous amplitude of the Q component can be found by

projecting the phasor onto the vertical (y) axis (Fig. 21).

For a phasor whose apparent rotation is counterclock-

wise—frequency of signal (represented by phasor) is higher

than frequency of reference signal (strobe light)—the I

component goes through its positive maximum 90˚ before

the Q component. On the other hand, for a phasor whose

apparent rotation is clockwise—frequency of signal repre-

sented by phasor is lower than that of reference—the Q

component goes through its maximum in a positive direc-

tion 90˚ before the I component.

Distinguishing Direction of Doppler Shifts. One of the

more striking examples of a requirement for resolving sig-

nals into I and Q components is found in radars that

employ digital doppler filtering. For digital filtering, the IF

output of the receiver must be converted to video frequen-

cies. To preserve the sense (positive or negative) of a target’s

doppler shift once this conversion has been made, two

video signals must be provided: one, corresponding to the

cosine of the doppler frequency (I); the other, to the sine

(Q). The reason is as follows.

21. Instantaneous values of the I and Q components of a signal are

obtained by projecting phasor representation of signal onto x as

well as y axis.

2. This convention was adopted

because current passing

through a resistance is in

phase with the voltage across

the resistance, whereas a cur-

rent passing through a reac-

tance either leads or lags

behind the voltage by 90˚.

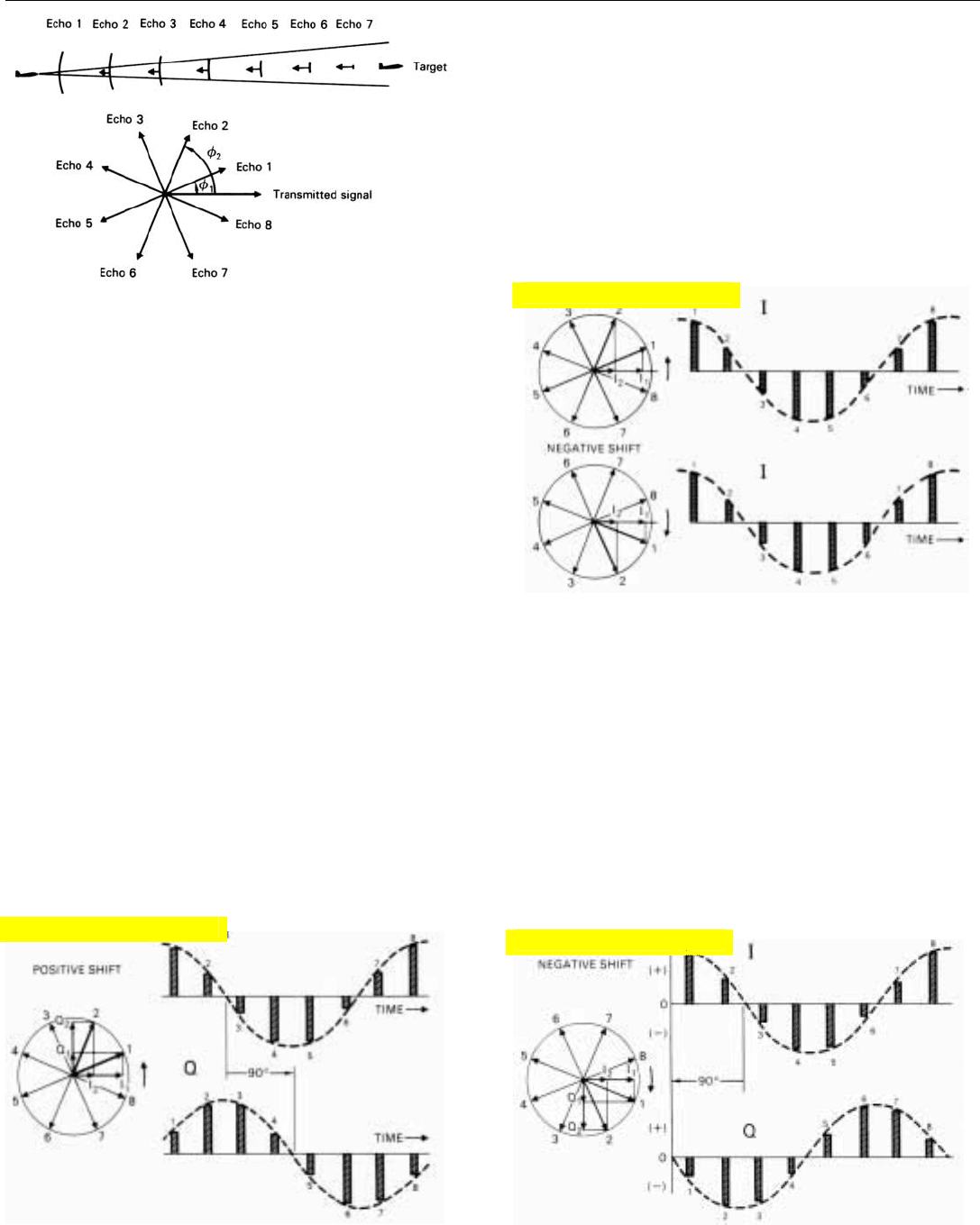
As will be explained in detail in Chap. 15, a target’s

doppler frequency shows up as a progressive shift in the

radio frequency phase, φ, of successive echoes received from

the target, relative to the phase of the pulses transmitted by

the radar. This echo-to-echo phase shift is illustrated by the

phasor diagram in Fig. 22.

By sensing the porgressive phase shift, the radar can pro-

duce a video signal whose amplitude fluctuates at the tar-

get’s doppler frequency. The signal is illustrated for positive

and negative doppler shifts in Fig. 23.

But as is clear from the figure, the fluctuations in the

amplitude if this signal are the same for both positive and

negative doppler shifts.

If both I and Q components of the phase shift are sensed,

however, the difference between positive and negative

doppler frequencies may be readily determined. For the

fluctuation of the Q components will lag behind the fluc-

tuation of the I component if the doppler shift is positive

(Fig. 24). And it will lead the fluctuation of the I compo-

nent if the doppler shift is negative.

22. A target

‘

s doppler frequency shows up as a pulse-to-pulse shift

in phase.

PART II Essential Groundwork

23. Video signal proportional to in-phase component of target

echoes fluctuates at target‘s doppler frequency; but fluctuation

is same for both positive and negative doppler shifts.

24. If the doppler frequency shift is positive and both I and Q

video signals are provided, Q will lag I by 90˚.

25. But if the doppler frequency shift is negative, Q will lead I by 90˚.

Click for high-quality image

CHAPTER 5 Key to a Nonmathematical Understanding of Radar

KEY TO A MATHEMATICAL UNDERSTANDING OF RADAR

Phasors are also the key to a mathematical understanding of

radar. For they enable one to visualize phase and frequency

relationships in the domain of the complex variable.

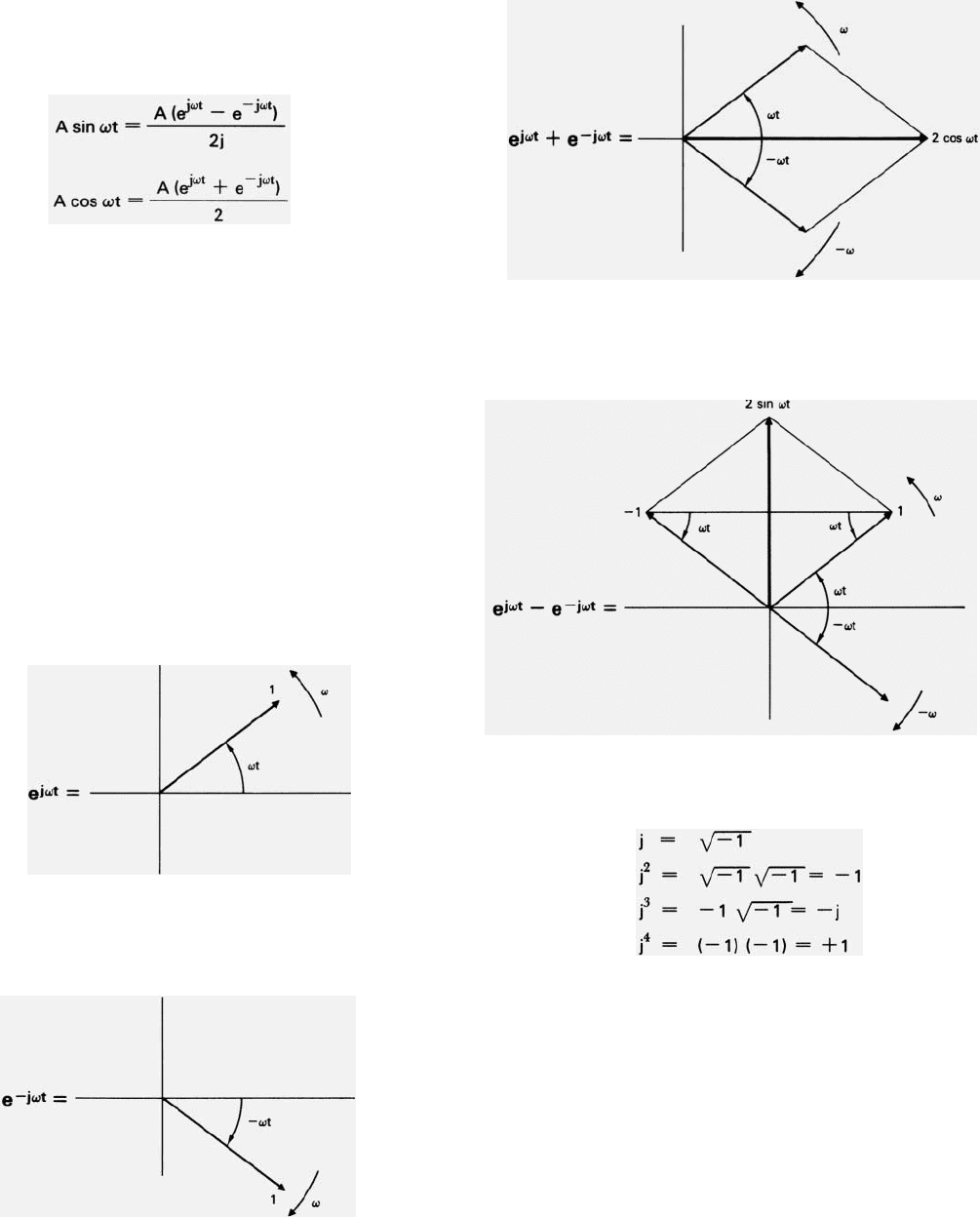
Sine and cosine functions can be expressed in exponential as

well as trignometric forms*

The letter “j” in the exponential terms stands for 公

–

–1.

Because 公

–

–1 alone cannot be evaluated, it is said to be an

“imaginary” number. A variable having an imaginary part and a

real part is called a complex variable.

Often, sinusoidal functions are more easily manipulated in the

exponential form than in the trigonometric form. Yet, for many

of us, the exponential terms, e

j␻t

and e

–j␻t

, alone, have little

physical meaning.

The functions they represent, however, can be visualized

quite easily with phasors. For this, e

is taken to mean rotation

in a counterclockwise direction and e

–j

, rotation in a clockwise

direction.

The term e

j␻t

then is represented by a phasor of unit length

rotating counterclockwise at a rate of ␻ radians per second.

The term e

–j␻t

is similarly represented by a phasor of unit

length rotating clockwise at a rate ␻.

The sum e

j␻t

+ e

–j␻t

equals the sum of the projections of the

two phasors onto the x axis. This sum, of course, is 2 cos ␻t.

The difference e

j␻t

– e

–j␻t

equals the projection of the first

phasor on the y axis minus the projection of the second pha-

sor on the y axis. This difference is 2 sin ␻t.

Using these basic relationships as building blocks and

remembering the values of j raised to various powers,

one can easily visualize virtually any relationships involving

the complex vanable.

* The equivalence can be demonstrated by expanding the functions sin x,

cos x, and e

into power series with Maclaurin’s theorem.

PART II Essential Groundwork

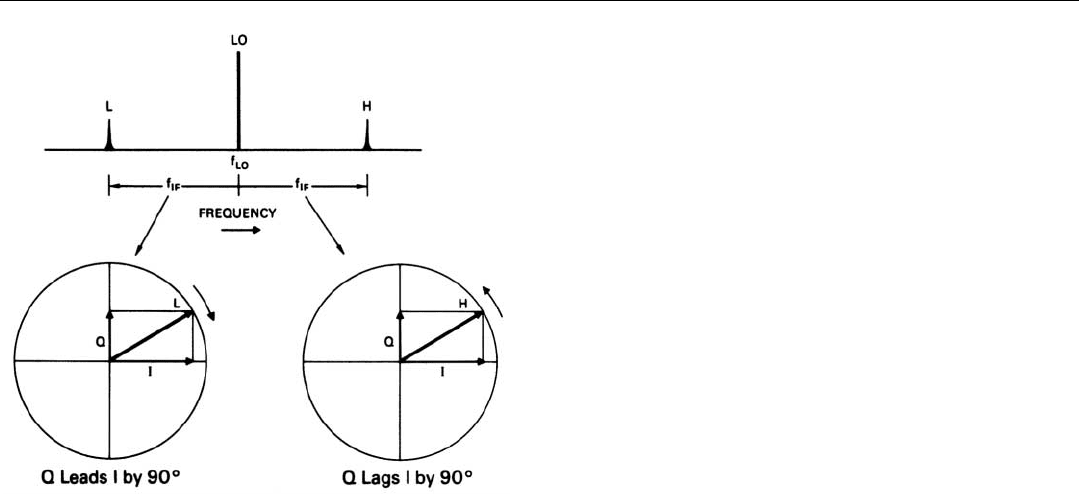
26. Quadrature component of mixer output will lead in-phase com-

ponent if frequency of received signal is lower than f

and

lag behind it if frequency of received signal is higher than f

Differentiating Between Signals and Images. Just as pos-

itive and negative doppler frequencies can be differentiated

by resolving the received signals into I and Q components

when they are converted from IF to video frequencies, so

also, images can be differentiated from signals when the

radar return is translated from the radar’s operating frequen-

cy to IF. As can be seen from the phasor diagram of Fig. 26,

if a signal’s frequency is higher than the local oscillator fre-

quency, the Q component of the mixer’s output will lag 90˚

behind the I component. Yet, if the signal’s frequency is

lower than the local oscillator frequency, the Q component

will lead the I component by 90˚. By taking advantage of

this difference, a receiver’s mixer stage can be designed to

reject images.

Summary

A powerful tool for visualizing phase and frequency rela-

tionships is the phasor. Its length corresponds to amplitude;

its rate of rotation, to frequency; its angle, to phase. The

phasor can be drawn in a fixed position by thinking of it as

being illuminated by a strobe light which flashes on at the

same point in every cycle. If the signal is in phase with the

reference, it is drawn horizontally.

If signals of the same frequency are combined, the ampli-

tude of the sum will depend on the relative phases of the

signals. Because of this dependence, even a very slight change

in target aspect can cause a target’s echoes to scintillate.

If signals of different frequency are combined, their sum

can be visualized by assuming the strobe is synchronized

with the rotation of one of the phasors, causing it to appear

fixed. The other then rotates at the difference frequency.

The amplitude and phase of the sum will be modulated

at a rate equal to the difference between the frequencies.

The phase modulation can be minimized by making the

second signal much stronger than the first. By extracting the

amplitude modulation, the first signal can be translated to

the difference frequency. At the same time, however, a signal

whose frequency is offset from that of the first signal by the

same amount in the opposite direction (image) will also be

translated to the difference frequency.

Whenever a carrier signal’s amplitude is modulated, two

sideband signals are produced. Their frequencies are sepa-

rated from the carrier by the modulation frequency.

Resolution of a signal into in-phase (I) and quadrature

(Q) components can be visualized by projecting the phasor

representing the signal onto the x and y coordinates.

Resolving the IF output of a receiver into I and Q components

when it is converted to video enables a digital filter to differen-

tiate between positive and negative doppler frequencies.

The Ubiquitous Decibel

1. Conceived for use in communications, the decibel was the

attenuation of one mile of standard telephone cable.

he decibel—or dB, as it is called—is one of the most

widely used tools of those who design and build

radars. If you are already familiar with decibels, can

readily translate to and from them, and feel at ease

when the experts start throwing them about, then skip this

short chapter. Otherwise, you will find the few minutes it

takes you to read it well worthwhile.

What Decibels Are

The decibel is a logarithmic unit originally devised to

express power ratios but used today to express a variety of

other ratios, as well. Specifically,

Power ratio in dB = 10 log

where P

and P

are the two power levels being compared. For

example, if P

is 1,000 then the power ratio in decibels is 30.

Origin. Named for Alexander Graham Bell, the unit origi-

nated as a measure of attenuation in telephone cable—the

ratio of the power of the signal emerging from a cable to the

power of the signal fed in at the other end. It so happened

that one decibel almost exactly equaled the attenuation of one

mile of standard telephone cable, the unit used until the deci-

bel came along (Fig. 1). Also, one decibel relative to the

threshold of hearing turned out to be very nearly the smallest

ratio of audio-power levels that could be discerned by the

human ear; so the dB was soon adopted in acoustics, too.

From telephone communications, the dB was quite naturally

passed on to radio communications; thence, to radar.

PART II Essential Groundwork

A SHORT COURSE IN LOGARITHMS

For years, logarithms to the base 10 were widely used to

simplify the multiplication and division of large numbers. With

the advent of the pocket calculator, however, logarithms to the

base 10 became largely obsolete. Consequently, many people

are today unfamiliar with them. For those who are (or have

forgotten), this brief review is provided.

What a Logarithm Is. Suppose that a number has a value, N.

Now suppose that n is the power to which 10 must be raised

to equal N.

The exponent n is the logarithm to the base 10 of N.

Logarithms of numbers that are whole multiples of 10 are

whole numbers.

N = 10

log

N = 3

N = 10

log

N = 2

Since 10

= 10 and 10

= 1, logarithms of numbers between

10 and 1 are decimal fractions.

N = 10 log

N = 1

↓↓

N = 1 log

N = 0

The logarithm of 2, for example, is 0.3.

Multiplying and Dividing with Logarithms. If two numbers

are expressed as powers of the same number, say 10, they

can be multiplied together by adding exponents.

 10

= 10

(3 + 2)

= 10

And one number can be divided by the other by subtracting

the exponent of the second from the exponent of the first.

 10

= 10

(3 – 2)

= 10

Consequently, numbers expressed as logarithms can be

multiplied or divided simply by adding or subtracting the

logarithms.

log

1000 . . . . . . . . . 3 log

1000 . . . . . . . . . 3

 log

100 . . . . . . . . . 2  log

100 . . . . . . . . . 2

log

(10

(3  2)

) . . . . . . 5 log

(10

(3  2)

) . . . . . . 1

Similarly, a number can be raised to any power by multiplying

its logarithm by that power.

log

1000  3

log

1000

 3  4  12

And any root of a number can be taken by dividing its logarithm

by that root.

log

1000  3

log

1000

1/4

 3  4  0.75

These are the characteristics that made logarithms to the base

10 so useful, prior to the era of the pocket calculator.

Logarithm of a Number Expressed in Scientific Notation.

Expressed in scientific notation, a number such as 200 is 2 

. The logarithm of the number, therefore, is the sum of the

logarithms of the two parts.

200  2  10

log

200  log

2  log

0.3  2  2.3

To express a number as a logarithm, therefore, one needs to

know only the logarithms of numbers between 1 and 10.

Converting from a Logarithm to dB. Going from the logarithm

of a power ratio to the value of the ratio in dB is but a short

step. You just multiply by 10. For example, if the number 200

was a power ratio (P

 200/1), the ratio expressed in dB

would be:

log

200  2.3

10 log

200  10  2.3  23 dB

CHAPTER 6 The Ubiquitous Decibel

3. Power ratios can be compounded simply by adding up their

decibel equivalents.

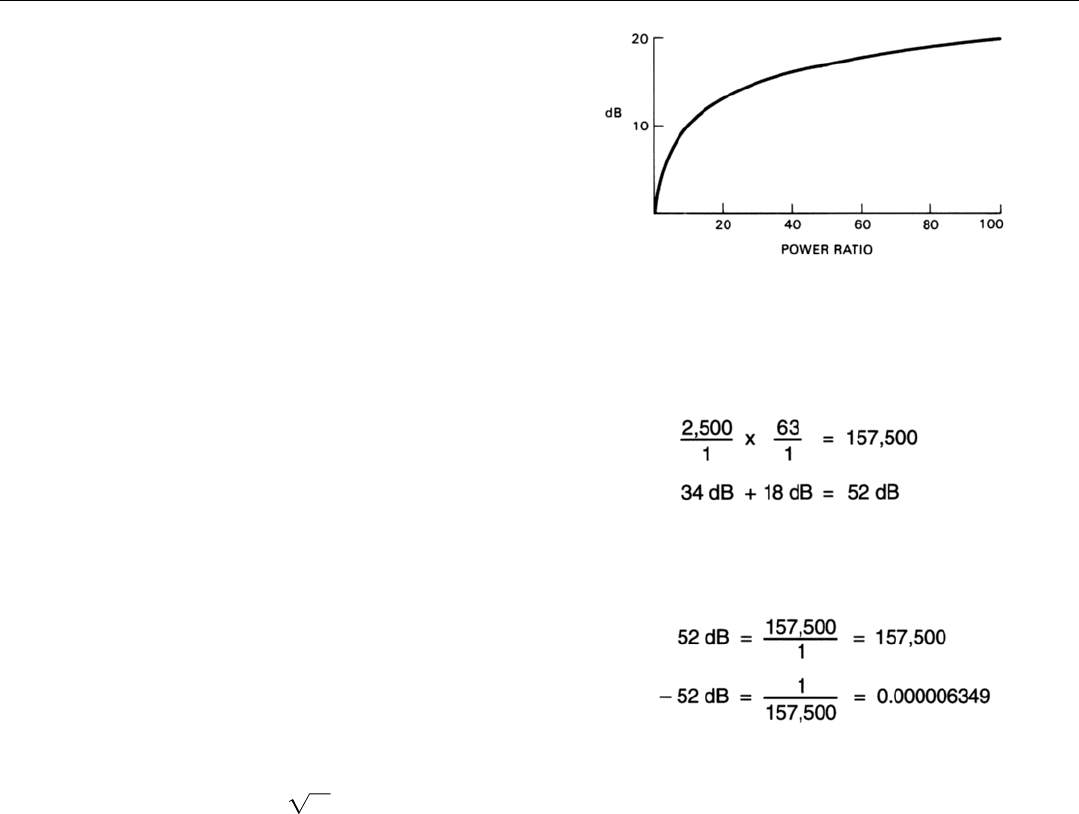
Advantages. Several features of the decibel make it par-

ticularly useful to the radar engineer. First, since the decibel

is logarithmic, it greatly reduces the size of the numbers

required to express large ratios (Fig. 2).

A power ratio of 2 to 1 is 3 dB; yet a ratio of 10,000,000

to 1 is only 70 dB. Since the power levels encountered in a

radar cover a tremendous range, the compression in the

sheer size of numbers that decibels provide is extremely

valuable.

Another advantage also stems from the decibel’s logarith-

mic nature: two numbers expressed as logarithms can be

multiplied simply by adding the logarithms. Expressing

ratios in decibels, therefore, makes compound power ratios

easier to work with. Multiplying 2500/1 by 63/1 in your

head for example, isn’t particularly easy. Yet when these

same ratios are expressed in decibels, there is nothing to it:

34 + 18 = 52 dB (Fig. 3).

Similarly, with logarithms, the reciprocal of a number

(one divided by the number) can be obtained simply by

giving the logarithm a negative sign. By merely changing

the sign of a ratio expressed in decibels, the ratio can

instantly be turned upside down. If 157,500 is 52 dB, then

/157,500 is –52 dB (Fig. 4).

When it comes to raising ratios to higher powers or tak-

ing roots, these advantages are magnified. If a ratio such as

63 is expressed in decibels, you can square it by multiply-

ing by two: 63

= 18 dB x 2 = 36 dB. You can take its

fourth root by dividing by four:

63 = 18 dB ÷ 4 = 4

/2 dB.

True, you can compress numbers by expressing them in

scientific notation (e.g., 20,000,000 = 2 x 10

). And you

can quickly multiply, divide, and take roots of numbers of

any size with a pocket calculator. But the decibel has the

advantage of incorporating the power of 10 right in its

value, thereby reducing the possibility of serious errors in

keeping track of decimal places. And you can manipulate

numbers that are expressed in decibels right in your head.

Furthermore, by tradition, many radar parameters are

commonly expressed in decibels.

Perhaps the most compelling advantage is this. In the

world of radar, where detection ranges vary as the one-

fourth power of most parameters, target signal powers may

vary by factors of trillions, and losses of 20 or 30 percent

may be negligible, it is a lot easier to talk and think in terms

of decibels than in terms of numbers expressed in scientific

notation or ground out of a calculator.

To be able to throw decibels about as deftly as a seasoned

radar engineer, you only need to know two things: (1) how

to convert from power ratios to decibels and vice versa;

(2) how to apply decibels to a few basic characteristics of a

2. Being logarithmic, the decibel greatly reduces the size of the

numbers required to express large power ratios.

4. A power ratio can be inverted by changing the sign of its

decibel equivalent.

PART II Essential Groundwork

radar. If you know the system, both things are surprisingly

easy. And the system is really quite simple.

Converting from Power Ratios to dB

You can convert any power ratio (P

/ P

) to decibels,

with any desired degree of accuracy, by dividing P

by P

finding the logarithm of the result, and multiplying by 10.

10 log

= dB

Nevertheless, for the accuracy you will normally want,

you don‘t need a calculator. With the method outlined

below, you can do it all in your head—provided you have

memorized a few simple numbers.

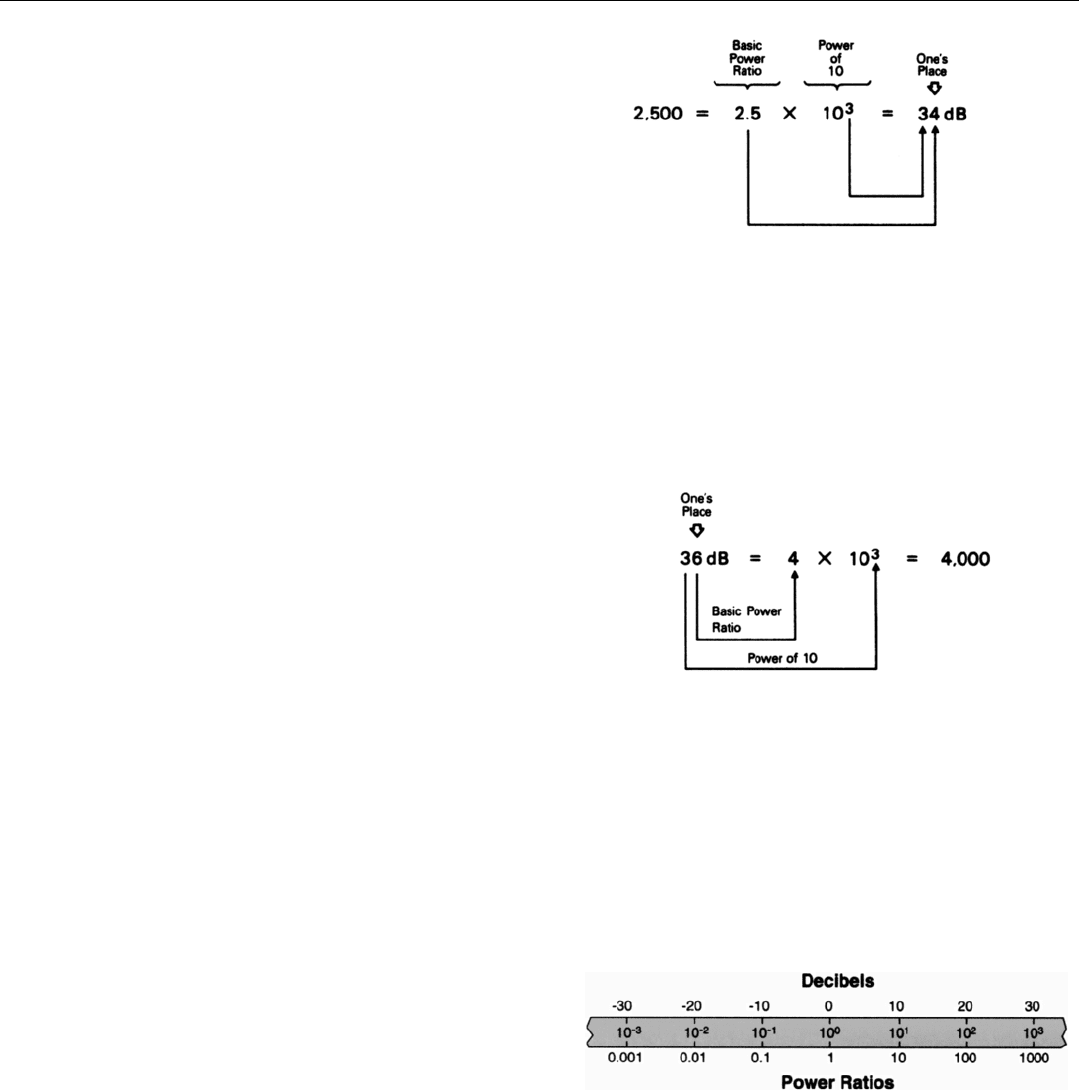
The first step is to express the ratio as a decimal number,

in terms of a power of 10 (scientific notation). A ratio of

10,000/4, for example, is 2500. In scientific notation,

2500 = 2.5 x 10

When converting to decibels, two portions of this expres-

sion are significant: the number 2.5, which we will call the

basic power ratio; and the number 3, which is the power of

10.

Now, a ratio expressed in decibels similarly consists of

two basic parts: (1) the digit in the “one’s place” (plus any

decimal fraction) and (2) the digit or digits to the left of the

one’s place. The digit in the one’s place expresses the basic

power ratio: 2.5, in the foregoing example. The digits, if any,

to the left of the one’s place express the power of 10: in this

case, 3.

Incidentally, as you may already have observed, if the

power ratio P

is rounded off to the nearest power of

10—e.g., 2.5 x 10

≈ 10

—converting it to decibels is a

trivial operation. The basic power ratio then is zero (log

= 0); so the decibel equivalent of P

is simply 10 times

the power of 10, in this case, 30. Thus,

Power Ratio Power of 10 dB

100

10 1 10

100 2 20

1000 3 30

10,000,000 7 70

The basic power ratio, of course, may have any value

from 1 to (but not including) 10. So, the digit in the one’s

place can be any number from 0 through 9.999…

Table 1. Basic Power Ratios

dB Power Ratio

1 1.26

2 1.6

4 2.5

5 3.2

8 6.3

CHAPTER 6 The Ubiquitous Decibel

Table 1 (opposite page) gives the basic power ratios for 0

to 9 dB. To simplify the table, all but the ratio for 1 dB have

been rounded off to two digits. If you want to become

adroit in the use of decibels, you should memorize these

ratios.

Returning to our example, if we look up the decibel equiv-

alent of the basic power ratio, 2.5, in Table 1 (or better yet,

our memory) we find that it is 4 dB. So, expressed in deci-

bels, the complete power ratio, 2.5

, is 34 dB (Fig. 5).

Converting from dB to Power Ratios

To convert from decibels to a power ratio, you can also

use a calculator. In this case, you divide the number of deci-

bels by 10 to get the power of 10; then raise 10 to that

power to get the power ratio.

Power ratio = 10

dB/10

But you can make the conversion just as easily in your

head, using the procedure outlined in the preceding para-

graphs in reverse.

Suppose, for example, you want to convert 36 dB to the

corresponding power ratio. The digit in the one’s place, 6, is

the dB equivalent of a power ratio of 4. The digit to the left

of the one’s place, 3, is the power of 10. The power ratio,

then, is 4 x 10

= 4,000 (Fig. 6).

As outlined here, the process may seem a bit laborious.

But once you’ve tried it a few times, there is really nothing

to it, if you remember the power ratios corresponding to

decibels 1 through 9. An easy way to remember them is

outlined in the panel on page 78.

Representing Power Ratios Less Than One

If 0 dB corresponds to a power ratio of one (1/1), how do

you convert power ratios that are less than one to decibels?

You use negative decibels, of course (Fig. 7). As previously

noted, a ratio expressed in decibels can be inverted by

putting a negative sign before it.

3 dB = 2

–3 dB =

/2 = 0.5

What about a power ratio of zero? The smaller the power

ratio is, the larger the number of negative decibels required

to represent it. As a ratio approaches zero, the number of

negative decibels increases without limit. For example, a

power ratio of

0.000,000,000,000,000,001 = –180 dB

There is no decibel equivalent of a power ratio of zero.

6. Conversion of decibels (36 dB) to a power ratio.

7. Negative decibels represent power ratios less than one; posi-

tive decibels, ratios greater than one; 0 dB, a ratio of 1.

5. Conversion of a power ratio (2,500) to decibels.