Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

PRE-PROCESSING OF TIME SERIES 9

1.4.1 Transformation of variables

Some types of time series obtained by counting numbers or by measur-

ing a positive-valued process, such as the prices of goods and numbers of

people illustrated in Figures 1.1(e) and 1.1(g), share the common chara c-

teristic that the variance of the series increases as the level o f the series

increases. For such a situation, we may construct a new series whose

variance is almost time-invariant and whose noise distribution is closer

to the normal distribution by using the log-transformation z

= logy

instead of the original series y

A more general Box-Cox transformation (Box and Cox (1964)) in-

cludes the log -transformation as a special case and the automatic deter-

mination of its parameter will be considered later in Section 4.8. For

time series y

that take values in (0,1) like probabilities or ratios of the

occurre nce of a cer tain phenomenon, we can obtain a time series z

that

takes a value in (−∞,∞) by the logit transformation

= log



1 −y



. (1.1)

In many cases, the distribution of the transformed time series z

less distorted than the original time series y

, thus the modeling of the

transformed series might be mo re tractable.

1.4.2 Differe ncing

When a time ser ie s y

contains a trend as seen in Figures 1.1(c), (e) and

(g), we might stu dy the differenced series z

deﬁned by (Box and Jenkins

(1970))

= ∆y

= y

−y

n−1

. (1.2)

This is motivated by the fact that, when y

is a straight line expressed as

= a + bn, then the differenced series z

becomes a constant as

= ∆y

= b, (1.3)

and the slope of the stra ight line can be removed.

Moreover, if y

is a parabola and expressed by y

= a + bn + cn

then the difference of z

becomes a constant and a and b are removed as

follows

∆z

= z

−z

n−1

10 INTRODUCTION AND PREPARATORY ANALYSIS

Figure 1.2: Difference of the logarithm of the Ni kkei 225 data.

= ∆y

−∆y

n−1

= (b + 2cn) −(b + 2c(n −1))

= 2c. (1.4)

When an annual cycle is observed in time series as shown in Figure

1.1(e), we m ight use the difference between the time series at the present

time and one cycle before deﬁned by

∆

= y

−y

n−p

. (1.5)

Figure 1.2 shows the difference of the loga rithm r

= logy

−

logy

n−1

of the Nikkei 225 data depicted in Figure 1.1( g), which is fre-

quently utilized in the analysis of ﬁnancial data in Japan. From Fig -

ure 1.2, it can be seen that the dispersion of the variation has changed

abruptly around n = 500. We shall discuss this phenomenon in detail

later in Sections 13.1 and 14.5.

1.4.3 Change from the previous month (quarter) and annual change

For economic time series as shown in Figure 1.1(e), we often consider

a change from the previous month (o r quarter) and an annual c hange of

the original series y

deﬁned by

n−1

, x

n−p

. (1.6)

If the time series y

is represented as the product of the trend T

and

the noise w

= T

, (1.7)

PRE-PROCESSING OF TIME SERIES 11

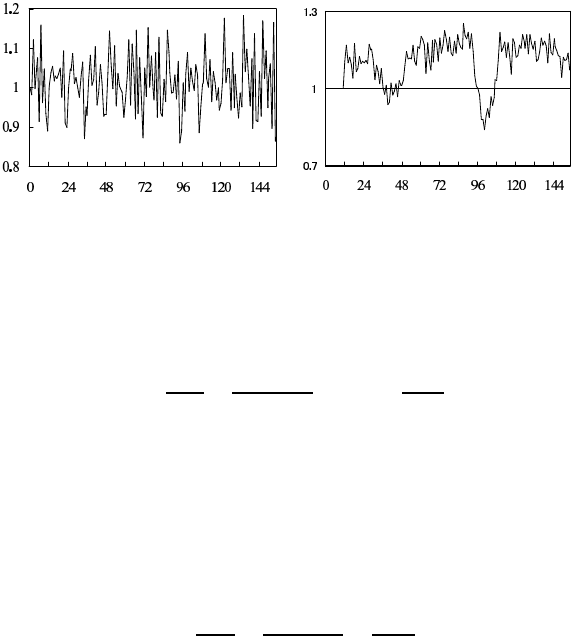
Figure 1.3 Change from previous month and year-over-year change of WHARD

data.

and T

evolves as T

= (1 +

n−1

, where

is the growth rate, then the

change from the previous month can be expressed by

n−1

= (1 +

)

n−1

. (1.8)

This means that, if the noise can be disregarded, the growth rate

can

be determin ed by this transformation.

On the other hand, if y

is represented as the product of a periodic

function s

with the cycle p and the noise w

= s

·w

, s

= s

n−p

(1.9)

then the annual changes x

can be expr essed by

n−p

. (1.10)

This suggests that the periodic function is removed by this transforma-

tion.

Figure 1.3 shows the change from the previous mon th and the annual

change of the WHARD d ata shown in Figure 1.1(e). The trend compo-

nent is rem oved by the change fr om the previous month. On the other

hand, the annual periodic component is removed by the annual change.

By me ans of this transformation, signiﬁcant drops a re revealed in the

vicinity of n = 40 and n = 100.

1.4.4 Moving average

Constructing a moving average is a simple method for smoothing time

series with random ﬂuctuations. For a time series y

, the (2k +1)-th te rm

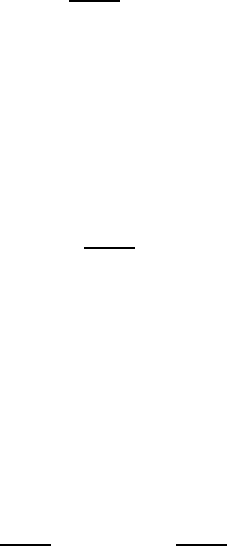
12 INTRODUCTION AND PREPARATORY ANALYSIS

moving average of y

is deﬁned by

2k + 1

∑

j=−k

n+ j

. (1.11)

When th e original time series is represented by the sum of the straight

line t

and the noise w

= t

+ w

, t

= a + bn, (1.12)

where w

is an independent noise with mean 0 and variance

, then the

moving average is given by

= t

2k + 1

∑

j=−k

n+ j

. (1.13)

Here, since the sum of the indepe ndent noises satisﬁes



∑

j=−k

n+ j



∑

j=−k

E[w

n+ j

] = 0,



∑

j=−k

n+ j





∑

j=−k

n+ j

)

= (2k + 1)

. (1.14)

Hence

Var



2k + 1

∑

j=−k

n+ j



2k + 1

. (1.15)

This shows that the mean of the moving average T

is the same as that

of t

, and the variance is reduced to 1/(2k + 1) of the variance of no ise

term w

Figure 1.4 shows the original maximum temperatu re data in Figure

1.1(c) an d its moving averages for k = 5,17 and 29. It can be seen that

the moving averages yield smoother curves as k b ecomes larger.

In general, the weighted moving average is deﬁned by

∑

j=−k

n−j

, (1.1 6)

where the weights satisfy

∑

j=−k

= 1 and w

≥ 0.

ORGANIZATION OF THIS BOOK 13

Figure 1.4 Maximum temperature data and its moving average. Top l eft: original

data, t op right: moving average wi th k = 5, bottom left: k = 17, bottom right:

k = 29.

If we modify the deﬁnition of a moving average by using the median

instead of the average, we obtain the (2k + 1)-th term moving median

that is deﬁned by

= media n {T

n−k

,···, T

n+k

}. (1.17)

The moving median can detect a change in the tren d more quickly than

can the moving average.

1.5 Organization of This Book

The main aim of this book is to provide basic tools for modeling vari-

ous time ser ies that arise for real-world problems. Chapters 2 and 3 are

basic chapters and introduce two descriptive a pproaches. I n chapter 2,

the autocovariance and autocorrelation functions are introduced as basic

tools to describe univariate stationary time series. The cross-covariance

and cross-co rrelation functions are also introduced for multivariate time

series. I n Chapter 3, the spectrum and the p e riodogram are introduced as

basic tools for th e frequen cy domain analysis of station ary time series.

For the multivariate case, the cross spectrum and the power contribution

are also introduced.

Chapters 4 and 5 discuss the basic metho ds for statistical model-

ing. I n Chapter 4, typic al probability distributions are introduced. Th en,

14 INTRODUCTION AND PREPARATORY ANALYSIS

based on the entropy maximization pr inciple, the likelihood function, the

maximum likelihood metho d and the AIC cr iterion are der ived. In Chap-

ter 5, under the assumption of linearity and normality o f the noise, the

least squares method is derived as a convenient method for ﬁtting various

statistical models.

Chapters 6 to 8 a re concerned with ARMA and AR models. In Chap-

ter 6, the ARMA model is introduced and the impulse response func-

tion, the autocovariance function, partial autocorrelation coefﬁcients, the

power spectrum and characteristic roots a re derived from the ARMA

model. The multivariate AR model is also considered in this chapter and

the cross-spectru m and power contribution are derived. The Yule-Walker

method and the least squares method for ﬁtting an AR mo del are shown

in Ch apter 7. In Chapter 8, the AR model is extended to the case wh ere

the time series is piecewise stationary and an application of the model to

the automatic determination of the change point o f a time series is given.

Chapter 9 introduces the state-space model as a uniﬁed way of ex-

pressing stationary and nonstationary time series models. The Kalman

ﬁlter and smooth er are shown to provide the conditional mean and vari-

ance of th e unknown state vector, given the observations. It is also shown

that we ca n get a uniﬁed method for prediction, interpolation and param -

eter estimation by using the state-space model and the Kalman ﬁlter.

Chapters 10 to 13 show examples of the application of the state-

space model. In Chapter 10, the exact maximum likelihood method for

the ARMA m odel is shown. The trend mode ls are introduced in Chapter

11. In Chapter 12, the seasonal adjustment model is introduced to de-

compose season al time series into several components such as the trend

and seasonal com ponents. Ch apter 13 is concerned with the modeling of

nonstationarity in the variance and covariance. Time-varying coefﬁcient

AR m odels are introduced and applied to the estimation of a changing

spectrum.

Chapters 14 a nd 15 are concerned with nonlinear no n-Gaussian state-

space models. In Chap te r 14, th e non-G a ussian state-space model is in-

troduced a nd a non-Gaussian ﬁlter an d smo other are derived f or state

estimation. Applications to the detection of sudden changes of the trend

component and other examples ar e p resented. In Chapter 15, the Monte

Carlo ﬁlter and smoother are introduced as a very ﬂexible method of ﬁl-

tering and smoothing for very general nonlinear non-Gaussian models.

Chapter 16 shows methods for g enerating various random numbe rs

and time series that follow an arbitrarily speciﬁed time serie s model.

Algorithms for nonlinear optimizatio n and the Mo nte Calro ﬁl-

ORGANIZATION OF THIS BOOK 15

ter/smoother and the derivations of the Levinson’s algorithm and the

Kalman ﬁlter are shown in Appendice s.

Problems

1. Wh a t is necessary to c onsider when discretizing a continu ous tim e

series?

2. Give an example of a non-Gaussian time series and describe its char-

acteristics.

3.(1) Obtain the inverse transformation of the logit transformation (1.1).

(2) Find a transformation fro m (a,b) to (−∞,∞) and ﬁnd its inverse.

4. Describe the problem in constructing a statio nary time series from a

nonstationary time series by differencing.

5. Describe the problem in removing cyclic compo nents by annual

changes.

6.(1) Show that if the true trend is a straight line, then the mean value

does not change for the three-term movin g average, and that the

variance bec omes 1/3 of the observed data variance.

(2) Discuss the differences between the char a cteristics of the moving

average ﬁlter and the moving median ﬁlter.

Chapter 2

The Covariance F unction

In this chapter, the covariance and correlation functions are presented

as basic methods to represent stationary time series. The autocovariance

function is a tool to represent the relation between past and present val-

ues of time series and the cross-covariance function is to express the

relation between two time series. T hese covariance functions are used to

capture features of time series to estimate the spectrum and to build time

series mode ls.

2.1 The Distribution of Time Series and Stationarity

The mean and the variance of data are fr equently used as basic statistics

to capture characteristics of ra ndom phenomena. A histogram is used to

represent ro ugh features of the data distribution. Therefore, by obtaining

the mean, the variance and the histogram, it is expected to capture some

aspects or features of th e data.

Accordingly, we shall investigate whether these statistics are useful

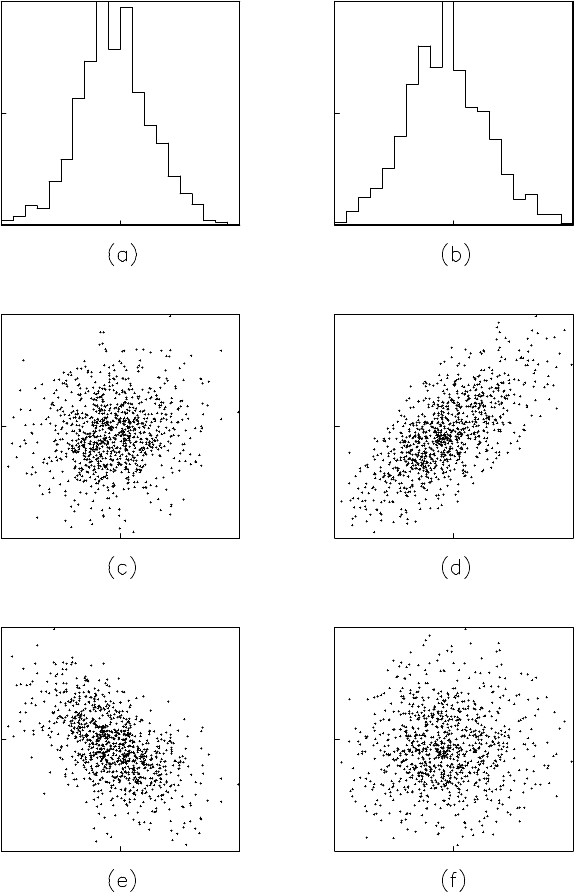
for the analysis of time series. The upper plots (a) and (b) in Figure 2.1

illustrate the histograms of the two time series (a) a ship’s yaw r ate a nd

(i) the ship’s rolling as shown in Figure 1.1. However, although the time

series in plot (a) of Figure 1.1 is apparently different from tha t in plot

(i) of Figu re 1.1, the histogram shown in Figure 2.1 (a) is quite similar

to that shown in (b) of Figure 2.1. This means that histograms cannot

capture some aspects of the chara cteristics of the time series that are

visually apparent.

Figures 2.1 (c) and (d) are scatterplots obtained by putting y

n−2

the horizontal axis and y

on the vertical axis, fo r the yaw rate and the

ship’s roll data , respectively. Similarly, Figures 2.1(e) and (f) show scat-

terplots obtained by pu tting y

n−4

on the h orizontal axis, again with the

time series as before. The scatterplot in (c) shows that the data are dis-

tributed evenly within a circle in the vicinity of the or igin and this indi-

cates that, in the c ase of the yaw rate, there is little correlation between

and y

n−2

18 THE COVARIANCE FUNCTION

Figure 2.1: Histograms and scatterplots of the yaw rate and rolling of a ship.