Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)
Подождите немного. Документ загружается.

xxii CONTENTS
14 Non-Gaussian State-Space Model 203
14.1 Necessity of Non-Gaussian Models 203
14.2 Non-Gaussian State-Space Models and State Estimation 204
14.3 Numerical Computation of the State Estimation Formula 206
14.4 Non-Gaussian Trend Model 209
14.5 A Time-Varying Variance M odel 213
14.6 Applications of Non-Gaussian State-Sp a ce Model 217
14.6.1 Processing of the outliers by a mixture of
Gaussian distributions 217
14.6.2 A non statio nary discrete proc e ss 218
14.6.3 A direct method of estimating the time-varying
variance 219
15 The Sequential Monte Carlo Filter 221
15.1 The Nonlinear Non-Gaussian State-Space Model and
Approximations of Distributions 221
15.2 Monte Carlo Filter 225
15.2.1 One-step-ahead pred ic tion 225
15.2.2 Filtering 225
15.2.3 Algorithm for the Monte Carlo filter 226
15.2.4 Likelihood of a model 226
15.2.5 Re-sampling method 227
15.2.6 Numerical examples 228
15.3 Monte Carlo Smoothing Method 231
15.4 Nonlinear Smoothing 233
16 Simulation 237
16.1 Generation of Uniform Random Numbers 237
16.2 Generation of Gaussian White Noise 239
16.3 Simulation Using a State-Spac e Model 241
16.4 Simulation with Non-Gaussian Model 243
16.4.1
χ
2
distribution 244
16.4.2 Cauchy distribution 244
16.4.3 Arbitrary distribution 244
A Algorithms for Nonlinear Optimization 249
B Derivation of Levinson’s Algorithm 251
CONTENTS xxiii
C Derivation of the Kalman Filter
and Smoother Algorithms 255
C.1 Kalman Filter 255
C.2 Smoothing 256
D Algorithm for the Monte Carlo Filter 259
D.1 One-Step-Ahead Predictio n 259
D.2 Filter 260
D.3 Smoothing 261
Answers to the Problems 263
Bibliography 277
Index 285

Chapter 1
Introduction and Preparatory Analysi s
In this chapter, various aspects of the classification of time series and the
objectives of time series modeling considered in th is book are discussed.
There are various types of time series, and it is very impo rtant to find out
the char a cteristics o f a time series by carefully looking at graphs of the
data befor e proceeding to the modeling and analysis phase. In the second
half of the chapte r, we shall consider various ways of pre-processing time
series that will be app lied before proceeding to time series modeling.
Finally, the organizatio n of the book is described.
1.1 Time Series Data
A record of phenomenon irregularly varying with time is c alled time
series. As examples of time series, we may consider meteorologica l data
such as atmo spheric pressur e , temperature, rainfall and the record s of
seismic waves; economic data such as stock prices and exchange rates;
medical data such as electroencephalogram a nd electrocardiograms, and
records of contr olling cars, ships and aircraft.
As a first step in the analysis of a time series, it is important to care-
fully examine graphs of the data. These su ggest various possibilities for
the next step in the analysis, together with a ppropriate strategies for sta-
tistical modeling.
Figure 1.1 shows several typical time series that will be analyzed
in subsequent chapter s as numerical examples. The followings are th e
features of the time series depicted in Figures 1.1 (a)–(i).
Plot (a) shows a time series of the yaw rate of a ship under navigation
in the Pacific Oc ean, observed every second. T he yaw rate fluctuates
around 0 degrees per second, b e cause the ship is under the control of
course keeping system (offered by Prof. K. Ohtsu of Tokyo University
of Marine Science and Technology).
Plot (b) shows a series of annual sunspot numbe r (Wolfer sunspot
number). Similar patterns of in crease and dec rease have been o bserved
over a cycle approximately ten years in length.
1

2 INTRODUCTION AND PREPARATORY ANALYSIS
Figure 1.1: Examples of various time series.
TIME SERIES DATA 3
Figure 1.1: Examples of various tim e series (continued).
Plot (c) shows the daily maximum temperatures for Tokyo recorded
for 16 months. Irregular fluctuations around the predominant annual pe-
riod ( trend) are seen (source: Tokyo District Meteo rological Observa-
tory).
Plot (d) shows the monthly time series of the number of workers en-
gaged in food ind ustries in the United States, called the BLSALLFOOD
data. The data reveal typical features of economic time series that co n-
4 INTRODUCTION AND PREPARATORY ANALYSIS
Figure 1.1: Examples of various time series (continued).
sists of trend an d seasona l components. The trend component gradu-
ally varies and the seasonal c omponent repeats a similar annua l pattern
(source: the U.S. Burea u of Labor Statistics (BLS)).
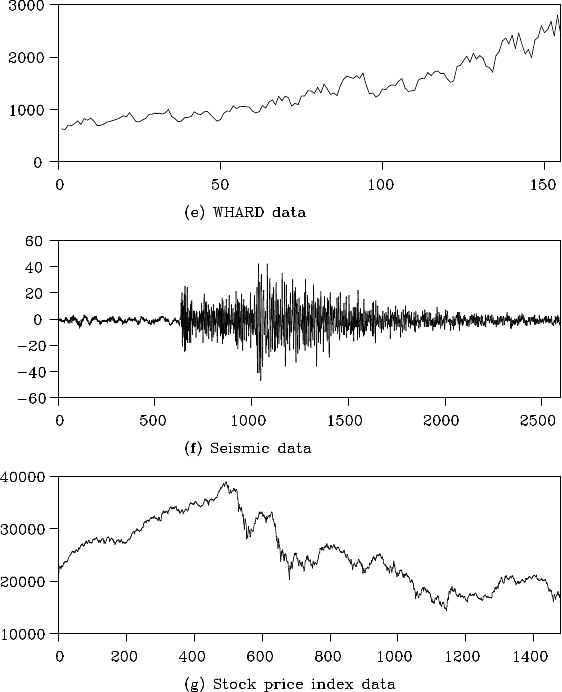
Plot (e) shows the monthly record of wholesale hardware data, called
WHARD data. This time series reveals typical characteristics of eco-
nomic data that increase at an almost fixed rate every ye ar, such tha t
the fluctuations around the trend gradually increase in magnitude over
time (source: U.S. Bureau of Labor Statistics).
Plot (f) shows the time series of East-West components of seismic
waves, recorded every 0.02 seconds. Because of the arrival of th e P-wave
(primary wave) and the S-wave (secondary wave), the variance of the
series changed significantly. Moreover, it can be seen that not on ly the
amplitude but also the freque ncy of the wave vary with time (Takanami
(1991)).
Plot (g) de picts the daily closing values of the Japanese stock price
index, Nikkei 2 25, quoted from January 4, 1988, to December 30, 1993.
It reveals a monotone increase in values until the end of 19 89, followed
by a gradual d ecrease with large re petitive fluctuations after the Bubble
crash in Japan in the 1990s. In the analysis of stock price data, we often
TIME SERIES DATA 5
Figure 1.1: Examples of various tim e series (continued).
apply various analysis m ethods after taking the difference of the log-
transformed data.
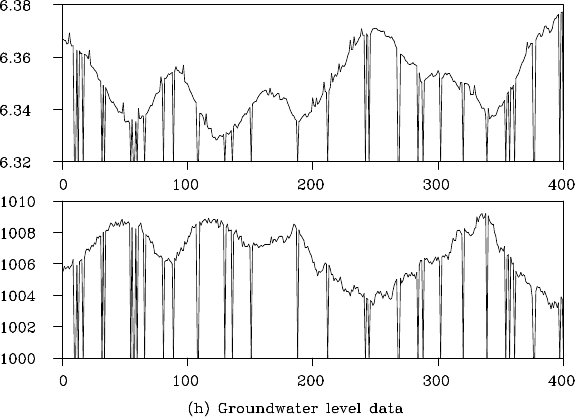
Plot (h) shows a bivariate time series of the groundwater level and
the atmospheric pressure that were observed at 10-min ute in tervals at
the obser vatory of the Tokai region, Japan, where a big earthquake was
predicted to occur. A part of the time serie s tha t takes values on the
horizontal axis, indicates missing observations, and some observations
that significantly deviate upward might be considered as outliers that oc-
curred due to malf unction of the observation device. To utilize the entire
informa tion contained in time series with ma ny missing and outlying ob-
servations recorded over many years, it is necessary to develop a method
6 INTRODUCTION AND PREPARATORY ANALYSIS
that can be applied to data with such missing and outlying observations
(offered by Dr. M. Takahashi and Dr. N. Matsumoto of National Institute
of Advanced Industrial Science and Technology).
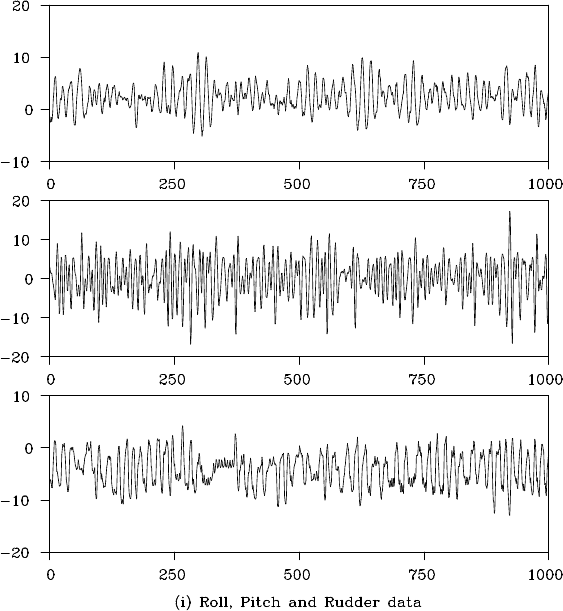
Plot (i) shows a m ultivariate time series of a ship’s rolling, pitching
and rudder angles recorded every second while navigating a cross the Pa-
cific Ocean. As for the rolling an d the rudder angles, both data show fluc-
tuations over a cycle of approximately 16 seconds. On the other hand, the
pitching angle varies over a sh orter cycle of 10 seconds or less (offered
by Prof. K. Ohtsu of Tokyo University of Marin e Science an d Technol-
ogy).
1.2 Classification of Time Series
As has been shown in Figure 1.1, there is a wide variety of time series
that can be classified into several categories from various viewpoints.
Continuous time series and discrete time series
Data continuously recorded, for example, by an analog device, are
called continuous time series. On the other hand, data observed a t cer ta in
intervals o f time, such as the atmospheric pressure measured hou rly, are
called discrete time series.
There a re two types of discrete time series; one where data observa-
tions are at equally spaced inte rvals and the othe r, where data observa-
tions are at unequally spaced intervals. Altho ugh the time series shown
in Figure 1.1 are connected con tinuously by solid lines, they are all d is-
crete time series. Her e after in this book, we consider only discrete time
series reco rded at equally spaced intervals, because time series that we
analyze on digital com puters are usually discrete time series.
Univariate and multivariate time series
Time series consisting of a single o bservation at e ach time point as
shown in Fig ures 1.1(a )–1.1(g) are called univariate time series. On the
other hand, time series that are obtaine d by simu ltaneously recording
two or more p henomena as the examples depicted in Figur e s 1.1(h)–
1.1(i) are called multivariate time series. However, it may b e difficult
to distinguish betwee n univariate and multivariate time series from their
nature; rather the distinction is made from the analyst’s viewpoint and b y
various oth e r factors such as the m easurement restriction and empirical
or theoretical knowledge about the subject. From a statistical modeling
point of view, variable selection itself is an important problem in time
series analysis.
CLASSIFICATION OF TIME SERIES 7
Stationary and nonstationary time series
A time series is a record of a phe nomenon irregularly varying over
time. In time series analysis, irregularly varying time series are generally
expressed by stochastic mod els. In some cases, a random phenomenon
can be co nsidered as a realization of a stochastic model with a time-
invariant structure. Such a time series is called a stationary time series.
Figure 1.1(a) is a typical example of a stationary time series.
On the other ha nd, if the stochastic structure of a time series itself
changes over time, it is called a nonstationary time series. As typical ex-
amples of n onstationary time series, consider the series in Figures 1.1(c),
(d), (e) and 1.1(g). It can be seen that mean values change over time in
Figures 1.1(c), ( d), (e) and 1.1(g) and the fluctuation around the mean
value changes over time in Figure 1.1(f).
Gaussian and non-Gaussian time series
When a distribution of a time series follows a normal distribution,
the time series is ca lled a Gaussian time series; oth erwise, it is called a
non-Gaussian time series. Most of the models considered in this book
are Gaussian models, under the assumption that the time series follow
Gaussian distributions.
As in the case of Figure 1.1(b) , the pattern of the time series is o cca-
sionally asymmetric so that the marginal distribution cannot be c onsid-
ered as Gaussian. Even in such a situation, we may obtain an approxi-
mately Gaussian time ser ie s by an app ropriate da ta transformation. This
method will be introduced in Section 1.4 and Section 4.5.
Linear and nonlinear time series
A time series that is expressible as the output of a linear model is
called a linear time series. In c ontrast, the output from a nonlinear model
is called a nonlinear time series.
Missing observations and outliers
In time series modeling of real-world problems, we sometime s need
to deal with missing observations and outliers. Some values of time se-
ries that have not been recorded for some re asons are called missing
observations in th e time series; see Figure 1.1(h). Outliers (outlying ob-
servations) might occur due to extraordinary behavior of the object, mal-
function of the observation device or errors in recording. I n the ground-
water level da ta shown in Figure 1.1(h), some data jumping up ward are
considered to be outliers.
8 INTRODUCTION AND PREPARATORY ANALYSIS
1.3 Objectives of Time Series Analy sis
This book presents statistical modeling methods for time series. The o b-
jectives of time series analysis considered in this book a re classified into
four categories; description, modeling, prediction and signal extraction.
Description: This includes methods that effectively express or sum-
marize the charac te ristics of time series. By drawing figures of time
series or by computing basic descriptive statistics, such as sample
autocorrelation functions, sample autocovariance functions and peri-
odograms, we may capture essential characteristics of the time series
and get a hint for time series modeling.
Modeling: In time series modeling, we capture the stochastic struc-
ture of time series by identifying an appropriate model. Sinc e there
are various types of time series, it is necessary to select an adequate
model class and to estimate parameters included in the mode l, de-
pending on the characteristics of the time series and the objective o f
the time series analysis.
Prediction: In the prediction of time series, based on the correlations
over time and among the variables, we can e stima te th e future behav-
ior of time series by using various information extracted from current
and past observations. In particular, in this book, we shall consider
methods of prediction and simulation based on the estimate d time se-
ries mod els.
Signal extraction: In signal extraction problems, we extract essential
signals or useful information from time series corresponding to the
objective of the analysis. To achieve that purpo se, it is important to
build models based on the salient characteristics of the object and the
purpose of the an a lysis.
1.4 Pre-processing of Time Series
For nonstation ary time series, we some times perform pre-pr ocessing of
the data before app lying the analysis metho ds that are introduced later in
this boo k. This section treats some methods of transfo rming nonstation-
ary time series into approximately stationary time series. In Chapter 11
and thereina fter, however, we shall introduce various methods for mod-
eling and analyzing nonstatio nary time series without pre-processing or
stationalization.
