Геллер Ю.А., Рахштадт А.Г. Материаловедение (методы анализа, лабораторные работы и задачи)

Подождите немного. Документ загружается.

На

основании анализа диаграммы состояния

Al—Si

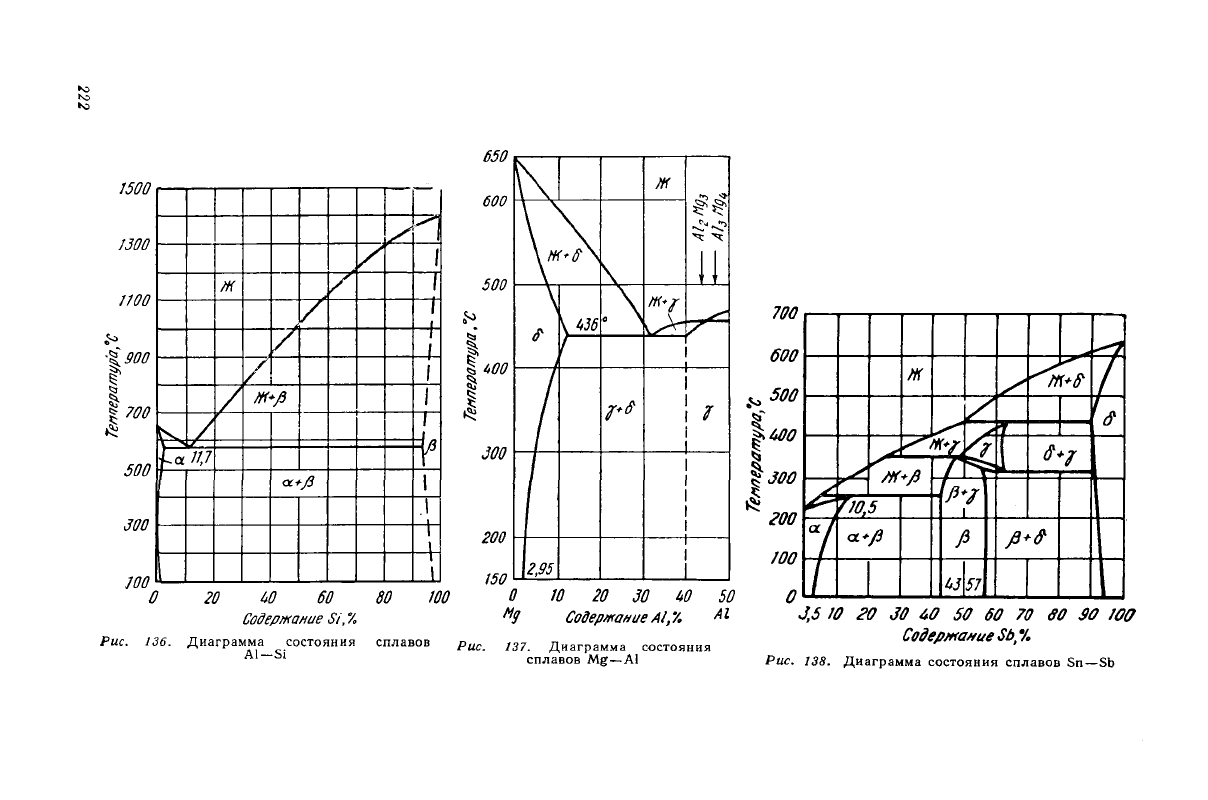
(рис. 136) и

зависимости, существующей

между

изменением литейных свойств и

видом диаграммы, определить состав силумина и указать, может ли

быть эффективной термическая обработка этого сплава.

Для решения задачи рассмотреть процессы превращений в сплавах

с 5, 12 и 20% Si и указать

структуру

и количественное соотношение

структур

при 20° С.

№

113. В системе магний—алюминий (рис. 137) имеются сплавы

на

основе магния, сильно упрочняющиеся в

результате

присутствия

алюминия

в определенных кон-

центрациях и выполнения тер-

мической

обработки. Эти спла-

вы,

как имеющие

малую

плот-

ность при удовлетворительной

прочности,

используются в ави-

ационной

других

отраслях

промышленности.

Рекомендовать состав спла-

ва и указать термическую обра-

ботку и фазу-упрочнитель.

Для решения задачи рас-

смотреть процессы превращений

сплавах с 1; 4 и 30% Mg и

определить

структуру

и коли-

чественное соотношение фаз в

этих сплавах при 20° С.

№

114. Подшипниковые спла-

вы (баббиты), используемые

виде литых вкладышей сколь-

жения

в тяжелонагруженных

механизмах, должны иметь

структуру

из твердых частиц, обеспечивающих износостойкость,

более мягкой металлической основы, окружающей эти частицы

создающей хорошую прирабатываемость вкладыша к поверхности

вращающегося вала. Для этой цели используют сплавы на основе

системы Sn—Sb определенного состава (рис. 138).

Указать, какой области диаграммы (см. рис. 69) должны соответ-

ствовать сплавы с подобной структурой и какие превращения проте-

кают в них при охлаждении после литья.

Для решения задачи рассмотреть процессы превращений в спла-

вах с 15, 50 и 80% сурьмы, определить их фазовый состав и количе-

ственное соотношение фаз при 20° С (учесть, что сурьма является

более твердым металлом, чем олово).

№

115. Сплавы системы Pb—Sb, отвечающие определенному

составу и

структуре

(баббиты), используют для литья вкладышей

скольжения

(работающих при умеренных нагрузках). Структура

сплавов должна состоять из пластичной металлической основы,

хорошо прирабатывающейся к

валу,

и твердых включений второй

фазы,

обеспечивающих износостойкость вкладыша.

two

tooo

300

| 600

500

300

гоо

600

~^05>

\ *

с;

С 5

—~ъ-

Си.Уо

+е/

1>(Ш1

)

20 30 ЬО 50

Содержанае

Си,%

Рис. 135. Диаграмма состояния

А1 —Си

60 70

221

КО

1500

1300

1100

700

500

300

100

К,

TattJ

650

600

500

600

300

200

150

2,95

\ 436

г/

ж*

1 7

700

600

500

20 40 60 80

Содержание

Si, %

100

О Ю 20 30 iO

Содержание

Al,У.

ТЮ,5

<х*/3

л*

из

Рис. 136. Диаграмма состояния сплавов

Al—Si

Рис. 137. Диаграмма состояния

сплавов

Mg—Al

гоо

юо

J.5 10 20 J0 ЛО 50 60 70 60 SO 100

Содержание

Sb,

Рис. 138. Диаграмма состояния сплавов Sn — Sb

Указать, какой из сплавов: с 5, 12 и 14—15% Sb более пригоден

для этого назначения (влияние меди и олова, дополнительно вводи-

мых в свинцовистые баббиты, можно условно не учитывать).

Для решения задачи рассмотреть процессы превращений в ука-

занных сплавах (см. рис. 65), указать их структуру и количествен-

ное

соотношение структурных составляющих при 20° С.

ГЛАВА

ЗАДАЧИ

ПО ДИАГРАММАМ СОСТОЯНИЯ

ТРОЙНЫХ СПЛАВОВ

ХАРАКТЕРИСТИКА

ДИАГРАММ

ТРОЙНЫХ

СПЛАВОВ

И МЕТОДИЧЕСКИЕ

УКАЗАНИЯ

ПО ИХ

АНАЛИЗУ

И РЕШЕНИЮ

ЗАДАЧ

Для определения в условиях равновесия фазового и структурного

состава тройных сплавов в зависимости от температуры и концен-

трации

применяют пространственные диаграммы, имеющие вид

трех-

гранных призм. Основанием призмы удобно выбирать равносторон-

ний

(«концентрационный*) треугольник, так как в таком треуголь-

нике

концентрацию всех компонентов можно показать в одинаковом

масштабе. Компоненты сплава располагают в вершинах треугольника,

концентрации

двойных сплавов — на соответствующих сторонах

треугольника, а тройные сплавы — внутри треугольника. Каждая

точка внутри треугольника характеризует тройной сплав определен-

ного состава.

Определение

концентрации

сплава

Концентрацию

любого тройного сплава можно определить не-

сколькими

способами:

1. Первый способ, называемый

способом

перпендикуляров,

осно-

ван

на известной из геометрии теореме о том, что

сумма

перпендику-

ляров,

опущенных

из

любой

точки

внутри

равностороннего

треуголь-

ника на

стороны,

равна

высоте

треугольника.

Последняя

прини-

мается за 100%, т. е. за сумму содержания всех трех компонентов

сплава, а длины перпендикуляров — за процентное содержание от-

дельных компонентов, составляющих тройной сплав. Поэтому пер-

пендикуляр, опущенный из вершины и, следовательно, совпадающий

с высотой и равный ей, указывает, что точки, лежащие в вершине,

соответствуют чистым компонентам и, в частности, 100% содержа-

ния

компонента, помещенного в вершине, из которой опущен пер-

пендикуляр. Например, на рис. 139 перпендикуляр Сс указывает,

что вершина С соответствует 100% содержания компонента С

сплаве, т. е. чистому компоненту С. Для определения концентра-

ции

тройного сплава, т. е. сплава, лежащего в какой-нибудь точке

внутри треугольника, необходимо опустить перпендикуляры из

этой

точки на стороны треугольника.

223

Длина перпендикуляра показывает концентрацию компонента,

помещенного в вершине, противоположной той стороне

треуголь-

ника,

на которую опущен перпендикуляр. Так, например,, на

рис.

139 длина перпендикуляра Ос показывает содержание компо-

нента

С в тройном сплаве, характеризуе-

мом точкой О; длина перпендикуляра

Оа — содержание компонента А в этом

же сплаве, а длина перпендикуляра

Ob — содержание компонента В. Дли-

ну перпендикуляра можно отсчитывать

по

масштабной сетке, наносимой внутри

треугольника.

Измерение

длины перпендикуляров

представляет некоторое

неудобство

связи

с тем, что концентрацию компо-

нентов,

составляющих сплав, отклады-

вают

на сторонах треугольника и, сле-

довательно, в масштабах, пропорцио-

нальных стороне (а не высоте)

треу-

гольника. В этих условиях затруднительно решение

обратной

за-

дачи, а именно нахождение точки внутри треугольника,

соответствую-

щей

составу

сплава, концентрация которого известна.

Рис. 139. Определение концентра-

ции

компонентов тройного сплава

по

способу перпендикуляров

Рис. 140. Определение концентрации компонентов тройного

сплава по способу параллелей:

а — определение по длине отрезков; б — выбор параллельных

отрезков

2. По второму способу, называемому

способом

параллелей,

кон-

центрацию компонентов измеряют по длине отрезков прямых, про-

водимых из точки искомого сплава параллельно стороне

треуголь-

ника

и до пересечения с

другой

его стороной. На рис. 140 видно, что

состав тройного сплава можно выразить не только длинами перпен-

дикуляров Оа, Ob и Ос, но и длинами отрезков Оа

и Ос

проведенных из точки О параллельно сторонам АВ, ВС и АС.

Эти отрезки

образуют

с перпендикулярами и с соответствующим

участком стороны равностороннего треугольника новые прямоуголь-

ные

треугольники, в которых опущенные перпендикуляры являются

224

катетами, а проведенные отрезки — гипотенузами, причем

угол

между

ними составляет 30°.

Все эти треугольники подобны и вследствие пропорциональности

между

катетами и гипотенузой в них сумма

всех

трех

отрезков

равна стороне треугольника, подобно тому как сумма опущенных пер-

пендикуляров равна высоте треугольника. Поэтому

измерение

по

катетам

можно

заменить

измерением

по

гипотенузам.

Оно имеет то

преимущество, что длины отрезков можно непосредственно опреде-

лять в масштабе, принятом для указанной концентрации на сторонах

треугольника.

Это правило относится не к любым трем отрезкам, полученным при

проведении через точку внутри треугольника линий параллельно

го зо ьо so во ю во 90

%в

so во 70 60 so ио зо го w

%А

Рис. 141. Проведение параллельных отрезков для определения концентрации

компонентов

тройного сплава

сторонам. Так, например, на рис. 140 сумма отрезков ОП! +0b

-f-

Ос

(или Of + Ое -\- Og) равна стороне треугольника, но сумма

отрезков Оа

-f Ogj

-+-

(или 0b

+ Ое -f- Ос) не равна стороне

треугольника. Во избежание ошибки

следует

выбирать такие три

отрезка,

угол

между

которыми составляет 120°.

Тогда для определения концентрации любого тройного сплава

через точку О проводят линии, параллельные сторонам треугольника

до пересечения с ними (рис. 141). Длина каждого из отрезков, отсе-

каемых на сторонах треугольника и заключенных

между

проведен-

ной

линией и параллельной ей стороной треугольника, определяет

содержание того компонента, который указан в вершине, противо-

положной

проведенной линии.

Так,

например, линия, проведенная на рис. 141, а параллельно

стороне треугольника АВ, отсекает на

двух

других

сторонах тре-

угольника отрезки В

и А

; эти отрезки равны гипотенузе Ор

прямоугольном треугольнике ОсР и длина их определяет содержа-

ние

компонента С в тройном сплаве,

225

Аналогично длина отрезка Ck или В1 (см. рис. 141) определяет

содержание компонента А, а длина отрезка Ар или Cd (или Ok) —

содержание компонента В в том же сплаве.

Применение

этого правила вызывает иногда некоторое затрудне-

ние,

ибо для указания процентного содержания компонентов на

сторонах треугольника нет установившегося правила: диаграммах,

приводимых в литературе, принят разный порядок указания кон-

центрации

компонентов, как например на рис. 141, а а б.

Хотя при определении концентрации сплава необходимо изме-

рять абсолютную длину отрезков, которая, конечно, не зависит от

порядка

расположения цифр на

диаграмме, однако различное рас-

положение их может затруднить

быстрый подсчет содержания

всех

трех

компонентов, тем более, что

при

проведении

трех

линий на сто-

ронах треугольника отсекается

шесть отрезков.

Можно

по этому способу опре-

делять концентрацию сплава не-

сколько

иначе. Из рассматривае-

мой

точки мысленно опускают

Содержание

В перпендикуляры на стороны тре-

Рис. ,42. Определение концентрации трои-

УГОЛЬНИКЭ.

Затем КЭЖДЫЙ

ПврПвН-

ного сплава по длине параллельных от-

ДИКУЛЯР

ПОВОраЧИВаЮТ

На 30 ППО-

резков

(с поворотом опушенных перпенди- J г г г

куляров на зо°) тив часовой стрелки, с тем чтобы

он

занял положение параллельно

стороне треугольника. Полученные отрезки проектируют на па-

раллельные им стороны треугольника.

В этом

случае

длина отрезков покажет концентрацию компонен-

тов, расположенных в вершинах, противоположных сторонам, на

которые были опущены перпендикуляры (рис. 142).

3. По третьему способу, называемому

правилом

трех

отрезков

более простому по выполнению, из рассматриваемой точки прово-

дят до пересечения с основанием треугольника две линии, параллель-

ные

двум

другим сторонам треугольника (рис. 143),

тогда

длина

отрезка kl, отсекаемого проведенными линиями на основании тре-

угольника, покажет содержание компонента С, расположенного в про-

тивоположной вершине; длина отрезка В1, прилегающего справа,

покажет содержание компонента, расположенного в левой вершине

(компонент

А на рис. 143, а), и соответственно длина отрезка Ak,

прилегающего слева, покажет содержание компонента, расположен-

ного в правой вершине (т. е. компонента В на рис. 143, а).

Это правило выводится из следующего. Треугольник Ю1, обра-

зуемый при проведении из точки О линий, параллельных сторонам

равностороннего треугольника ABC, подобен треугольнику ABC

(рис.

143, б) и, следовательно, также является равносторонним.

Правило предложено Ю. А. Геллером (прим. ред.).

226

Стороны

01 и Ok треугольника kOl являются гипотенузами в прямо-

угольных треугольниках kOn и Юп. Было показано, что длина этой

гипотенузы определяет содержание компонента С; следовательно,

сторона kl, равная Ю и 01 (в равностороннем треугольнике Okl),

также определяет содержание компонента С.

На

рис. 143, б показано, что аналогично длина стороны Ор

треугольника pOS определяет содержание компонента А, но отрезки

Содержание

a S

Рис. 143. Определение концентрации тройного сплава по правилу стрех отрезков»:

а — определение концентраций; б — доказательство правила

Ор и 1В равны (как два отрезка параллельных, заключенных

между

параллельными). Таким же образом доказывается, что длина от-

резка Ak определяет содержание компонента В.

Это правило применимо только для определения концентрации

сплава, и из приведенного построения нельзя сделать вывод о том,

что сторона треугольнка, характеризуя строение сплава из

двух

ком-

понентов,

может характеризовать строение тройного сплава.

Пространственные

диаграммы

Равносторонний

треугольник служит основанием трехгранной

призмы;

температуры откладывают по высоте призмы. Такое по-

строение

дает

пространственную диаграмму (или объемную модель).

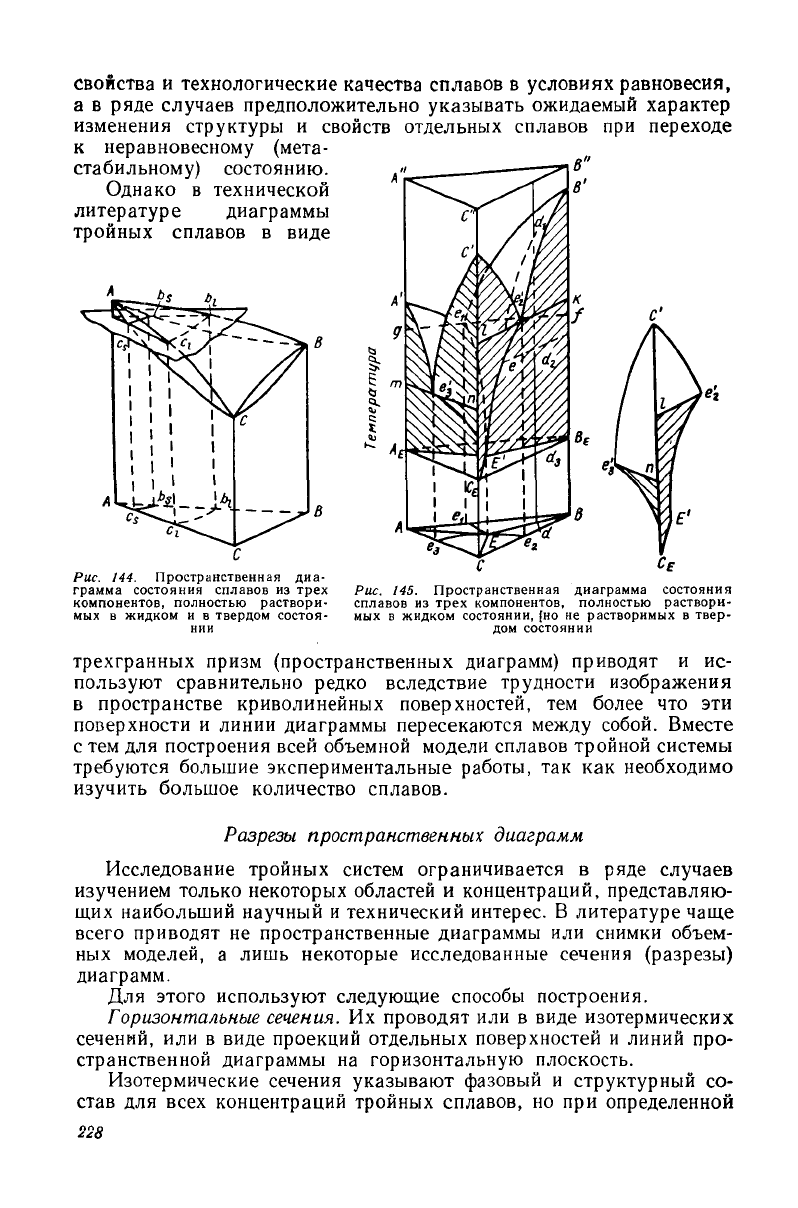
На

рис. 144 и 145 приведены в качестве примеров пространствен-

ные

диаграммы сплавов из

трех

компонентов: а) полностью раство-

римых в жидком и в твердом состоянии (рис. 144); б) полностью рас-

творимых в жидком состоянии, но не растворимых в твердом состоя-

нии

(рис. 145).

Рассмотрение диаграмм тройных сплавов позволяет, как и по

диаграммам двойных сплавов, определять фазовый и структурный

состав, качественно оценивать многие физически-е и механические

227

свойства и технологические качества сплавов в условиях равновесия,

а в ряде случаев предположительно указывать ожидаемый характер

изменения

структуры и свойств отдельных сплавов при переходе

неравновесному (мета-

стабильному) СОСТОЯНИЮ.

Однако в технической

литературе диаграммы

тройных сплавов в виде

Рис. 144. Пространственная диа-

грамма состояния сплавов из

трех

компонентов,

полностью раствори-

мых в жидком и в твердом состоя-

нии

Рис. 145. Пространственная диаграмма состояния

сплавов из

трех

компонентов, полностью раствори-

мых в жидком состоянии, [но не растворимых в твер-

дом состоянии

трехгранных призм (пространственных диаграмм) приводят и ис-

пользуют сравнительно редко вследствие трудности изображения

пространстве криволинейных поверхностей, тем более что эти

поверхности и линии диаграммы пересекаются

между

собой. Вместе

с тем для построения всей объемной модели сплавов тройной системы

требуются большие экспериментальные работы, так как необходимо

изучить большое количество сплавов.

Разрезы

пространственных

диаграмм

Исследование тройных систем ограничивается в ряде случаев

изучением только некоторых областей и концентраций, представляю-

щих наибольший научный и технический интерес. В литературе чаще

всего приводят не пространственные диаграммы или снимки объем-

ных моделей, а лишь некоторые исследованные сечения (разрезы)

диаграмм.

Для этого используют следующие способы построения.

Горизонтальные

сечения.

Их проводят или в виде изотермических

сечений,

или в виде проекций отдельных поверхностей и линий про-

странственной диаграммы на горизонтальную плоскость.

Изотермические сечения указывают фазовый и структурный со-

став для

всех

концентраций тройных сплавов, но при определенной

228

температуре. Эти сечения представляют собой равносторонний тре-

угольник, если последний при построении пространственной диа-

граммы был принят за основание призмы.

Изотермические сечения удобны в том отношении, что позволяют

определить фазовый и структурный состав сплавов данной тройной

системы, если на них нанесены коноды. Однако недостатком этого

построения

является невозможность определения, как изменяется

фазовый

или структурный состав в зависимости от температуры.

Следовательно, рассмотрение одного такого сечения не позволяет

судить о многих свойствах тройных сплавов и, в частности, о

ходе

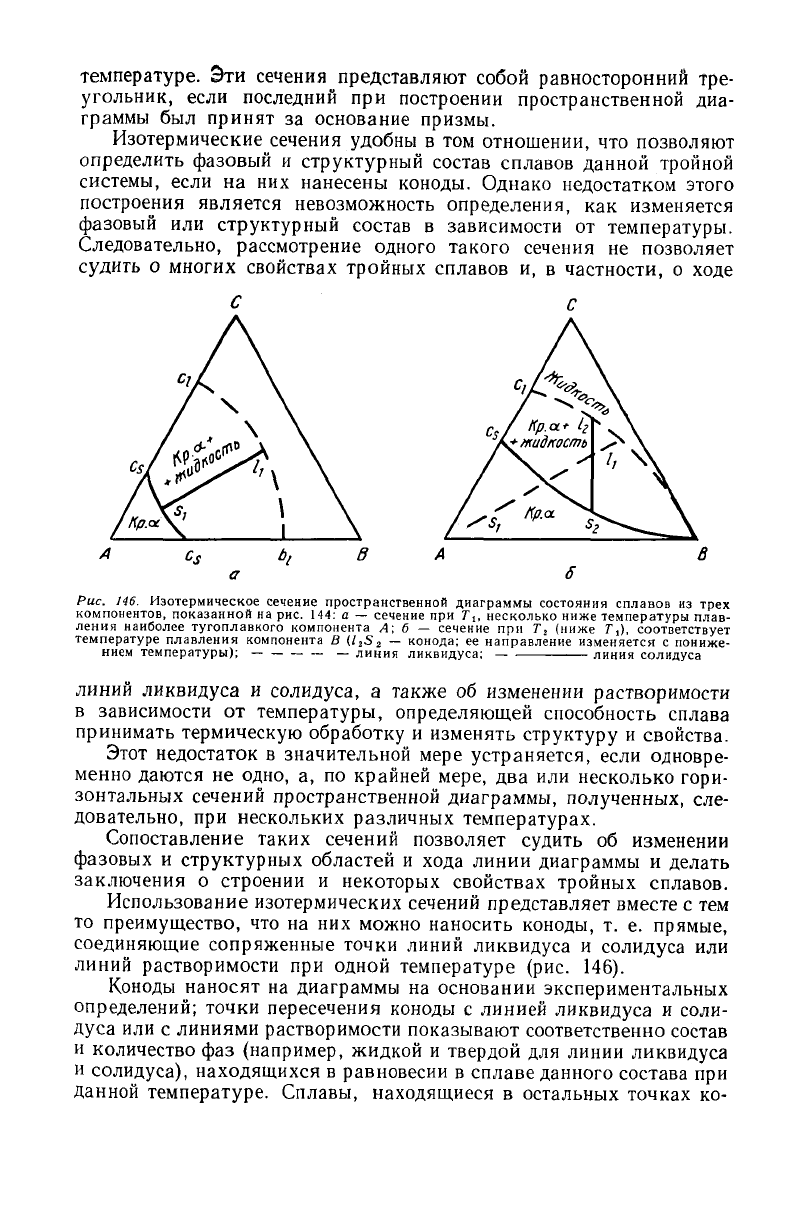
Рис. 146. Изотермическое сечение пространственной диаграммы состояния сплавов из

трех

компонентов,

показанной на рис. 144: а — сечение при 7\, несколько ниже температуры плав-

ления

наиболее тугоплавкого компонента А; б — сечение при Т

(ниже 7",), соответствует

температуре плавления компонента В (1

— конода; ее направление изменяется с пониже-

нием

температуры); — линия ликвидуса; линия солидуса

линий

ликвидуса и солидуса, а также об изменении растворимости

зависимости от температуры, определяющей способность сплава

принимать

термическую обработку и изменять

структуру

и свойства.

Этот недостаток в значительной мере устраняется, если одновре-

менно

даются не одно, а, по крайней мере, два или несколько гори-

зонтальных сечений пространственной диаграммы, полученных, сле-

довательно, при нескольких различных температурах.

Сопоставление таких сечений позволяет судить об изменении

фазовых и структурных областей и

хода

линии диаграммы и делать

заключения о строении и некоторых свойствах тройных сплавов.

Использование

изотермических сечений представляет вместе с тем

то преимущество, что на них можно наносить коноды, т. е. прямые,

соединяющие сопряженные точки линий ликвидуса и солидуса или

линий

растворимости при одной температуре (рис. 146).

Коноды

наносят на диаграммы на основании экспериментальных

определений; точки пересечения коноды с линией ликвидуса и соли-

дуса

или с линиями растворимости показывают соответственно состав

количество фаз (например, жидкой и твердой для линии ликвидуса

солидуса), находящихся в равновесии в сплаве данного состава при

Данной

температуре. Сплавы, находящиеся в остальных точках ко-

ноды,

имеют одинаковый фазовый состав, но разное количественное

соотношение фаз.

Проекции

поверхностей и линий пространственной диаграммы на

горизонтальную плоскость обычно образуют концентрационный тре-

угольник, на который наносят (проектируют) линии пространственной

диаграммы, разные точки которых соответствуют различным темпе-

ратурам (т. е. разным изотермическим сечениям). Например, так

наносят

линии двойных эвтектик для сплавов, образующих эвтек-

тические смеси, и точку, определяющую концентрацию тройной

эвтектики

(рис. 147), и указывают на диаграмме температуры обра-

зования

эвтектик. В дан-

ном

случае

можно судить о

протекании

процесса кри-

сталлизации.

На

концентрационный

треугольник можно проек-

тировать также поверхно-

сти ликвидуса и солидуса,

линии

растворимости и ли-

нии,

которые характери-

зуют

сплавы, обладающие

некоторыми

одинаковыми

свойствами, например оди-

наковой

твердостью.

На

одну диаграмму це-

лесообразно наносить

лишь

некоторые линии,

так

как проектирование

всех

линий, характеризую-

щих фазовый состав или

определенные свойства сплавов, усложняет диаграмму.

Однако использование горизонтальных сечений не позволяет по-

строить полную кривую охлаждения или нагревания каждого трой-

ного сплава, как это можно сделать на диаграмме двойных сплавов.

Вертикальные

разрезы

(сечения). Эти разрезы указывают каче-

ственно фазовый и структурный состав сплавов при

всех

температу-

рах, но только для некоторых концентраций тройных сплавов, опре-

деляемых в зависимости от того, как проведено сечение простран-

ственной

диаграммы.

Применяют

следующие разрезы:

а) разрез параллельно одной из сторон концентрационного тре-

угольника (т. е. параллельно одной из граней призмы). В этом

случае

содержание одного из компонентов (для разреза, показанного на

рис.

148, а, содержание компонента С) остается постоянным, а

двух

других

(А и В) — переменным от точки а до точки Ь;

б) разрез через одну из вершин концентрационного треуголь-

ника,

т. е. через ребро призмы по ее высоте или параллельно высоте

(рис.

148, б), или под тем или иным

углом

в направлении, не совпа-

дающем с высотой (рис. 145, в). Во

всех

этих случаях при изменении

230

10 20

271°

Рис. 147. Проекция поверхностей ликвидуса спла-

вов Pb—Sn —Bi