Geiser J. Decomposition Methods for Differential Equations: Theory and Applications
Подождите немного. Документ загружается.


96Decomposition Methods for Differential Equations Theory and Applications
4.5 Nonlinear Iterative Operator-Splitting Methods
In this chapter we deal with the nonlinear operators. Behind is the lineariza-
tion with the Newton method. We could linearize the nonlinear operators and
deal with linear methods.
4.5.1 Linearization with the Waveform Relaxation
We can formulate the operator-splitting methods into waveform-relaxation
methods. This generalization helps us to unify the theory around the splitting
methods.
F
i
(t, u, v)=f
i
(t, v
1
,v
2
,...,v
i−1
,u
i
,...,u
d
)
+
∂f
i
∂v
i
(t, v
1
,...,v
i−1
,u
i
,...,u
d
)
(v
i
− u
i
), (4.100)
where the iteration is the Gauss-Seidel-waveform-relaxation Newton method,
cf. [194].
For the two operator equation,
∂
t
c = A(c)+B(c) (4.101)
we use the linearization
A(c
i
) ≈ A(c
i−1
)+A
(c
i−1
)(c
i
− c
i−1
) (4.102)
and obtain the following linearized equation:
∂
t
c
i
= A(c
i−1
)+A
(c
i−1
)(c
i
− c
i−1
)+B(c
i−1
)+B
(c
i−1
)(c
i
− c
i−1
),
where i is the iteration index, A
the Jacobian matrix of A,andwestartwith
the initial value c
0
= c(t
n
).
We can rewrite the equation system as a formal A-B splitting:
∂
t
c
i,∗
= A(c
i−1,∗
)+A
(c
i−1,∗
)(c
i,∗
− c
i−1,∗
), (4.103)
with c
i,∗
(t
n
)=c(t
n
),
∂
t
c
i,∗∗
= B(c
i−1,∗∗
)+B
(c
i−1,∗∗
)(c
i,∗∗
− c
i−1,∗∗
), (4.104)
with c
i,∗∗
(t
n
)=c(t
n
),.
where i =1, 2,...,M and the stop criterion is given as
min(|c
i,∗
− c
i−1,∗
|, |c
i,∗∗
− c
i−1,∗∗
|)=err,anderr ∈ R
+
.
REMARK 4.15 The nonlinear iterative operator-splitting method
can be discussed with different linearization techniques, see [92]. The lin-
earization techniques are taken into account Newton’s method or fixpoint
schemes, see more results in [93].
© 2009 by Taylor & Francis Group, LLC

Chapter 5
Spatial Decomposition Methods
5.1 Domain Decomposition Methods Based on Iterative
Operator-Splitting Methods
The combined spatiotemporal iterative operator-splitting method combines
the Schwarz waveform-relaxation and the iterative operator-splitting method.
The following algorithm iterates with a fixed splitting discretization step
size τ. On the time interval [t
n
,t
n+1
], we solve the following subproblems
consecutively for i =1, 3,...2m +1 and j =1, 3,...2m + 1. In this notation,
i represents the iteration index for the temporal splitting and j represents the
iteration index for the spatial splitting.
dc
i,j
(t)
dt
= A|
Ω
1
c
i,j
(t)+A|
Ω
2
c
i,j−1
(t)
+ B|
Ω
1
c
i−1,j
(t)+B|
Ω
2
c
i−1,j−1
(t),
with c
i,j
(t
n
)=c
n
, (5.1)
dc
i+1,j
(t)
dt
= A|
Ω
1
c
i,j
(t)+A|
Ω
2
c
i,j−1
(t)
+ B|
Ω
1
c
i+1,j
(t)+B|
Ω
2
c
i−1,j−1
(t),
with c
i+1,j
(t
n
)=c
n
, (5.2)
dc
i,j+1
(t)
dt
= A|
Ω
1
c
i,j
(t)+A|
Ω
2
c
i,j+1
(t)
+ B|
Ω
1
c
i+1,j
(t)+B|
Ω
2
c
i−1,j−1
(t),
with c
i,j+1
(t
n
)=c
n
, (5.3)
dc
i+1,j+1
(t)
dt
= A|
Ω
1
c
i,j
(t)+A|
Ω
2
c
i,j+1
(t)
+ B|
Ω
1
c
i+1,j
(t)+B|
Ω
2
c
i+1,j+1
(t),
with c
i+1,j+1
(t
n
)=c
n
, (5.4)
where c
0,0
(t),c
1,0
(t), and c
0,1
(t) are fixed functions, for example, c
0,0
(t)=
c
1,0
(t)=c
0,1
(t) = 0, for each iteration. c
n
is the known split approximation
atthetimelevelt = t
n
, cf. [70]. The boundary conditions are Neumann
conditions that are embedded in the equations, see Chapter 2 and [178]. We
have the domain Ω with Ω = Ω
1
∪ Ω
2
,Ω
1
∩ Ω
2
=Ω
1,2
and the restriction
97
© 2009 by Taylor & Francis Group, LLC
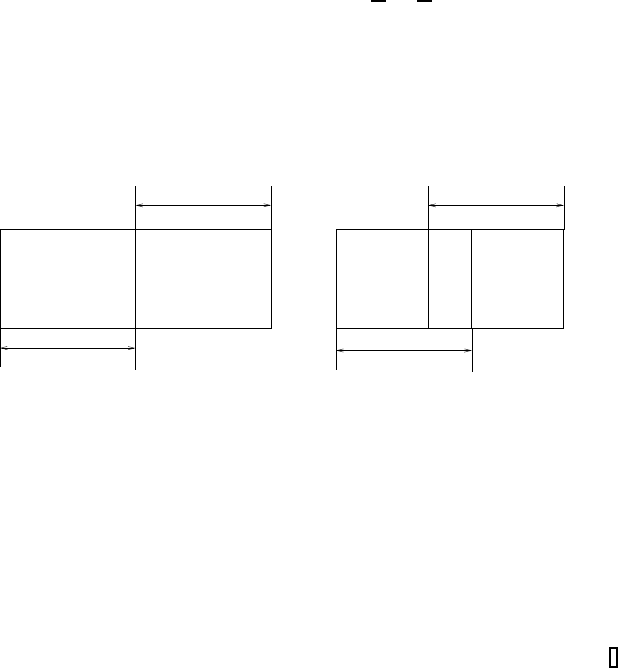
98Decomposition Methods for Differential Equations Theory and Applications
to each operator that is, A|
Ω
i
,B|
Ω
i
with i =1, 2fortwosubdomains. The
coupling is done at the intermediate boundaries
Ω
1
∩ Ω
2
=Γ
Ω
1
,Ω
2
(Ω
1,2
= ∅,
i.e. mass zero, see [179]) for the nonoverlapping method or at the overlapping
set (Ω
1,2
= ∅, i.e., of mass 1, see [179]) for the overlapping method. The
overlaps are presented in Figure 5.1.
Ω
1
Ω
2
Ω
1
Ω
2
Overlapping
Nonoverlapping
FIGURE 5.1: Graphical visualization of the overlaps.
REMARK 5.1 We extend the splitting method with respect to the
underlying spatial discretized operators. For each subdomain, we redefine the
corresponding operators into the subdomain.
5.1.1 The Nonoverlapping Spatiotemporal Iterative
Splitting Method
For the semi-discretization in space, we introduce the variable k as the
node for the point x
k
, and we have k ∈{0,...,p},wherep is the number of
nodes. We concentrate on the one-dimensional nonoverlapping case. For the
nonoverlapping case we assume the decomposition in space, where Ω
1
consists
of the points 0,...,p/2, and Ω
2
consists of p/2+1,...,p, whereby we assume
© 2009 by Taylor & Francis Group, LLC

Spatial Decomposition Methods 99
p to be even. Thus, we assume Ω
1
∩Ω
2
= ∅ leading to the following algorithm:
d(c
i,j
)
k
(t)
dt
=
˜
A|
Ω
1
(c
i,j
)
k
(t)+
˜
A|
Ω
2
(c
i,j−1
)
k
(t)
+
˜
B|
Ω
1
(c
i−1,j
)
k
(t)+
˜
B|
Ω
2
(c
i−1,j−1
)
k
(t),
with (c
i,j
)
k
(t
n
)=(c
n
)
k
, (5.5)
d(c
i+1,j
)
k
(t)
dt
=
˜
A|
Ω
1
(c
i,j
)
k
(t)+
˜
A|
Ω
2
(c
i,j−1
)
k
(t)
+
˜
B|
Ω
1
(c
i+1,j
)
k
(t)+
˜
B|
Ω
2
(c
i−1,j−1
)
k
(t),
with (c
i+1,j
)
k
(t
n
)=(c
n
)
k
, (5.6)
d(c
i,j+1
)
k
(t)
dt
=
˜
A|
Ω
1
(c
i,j
)
k
(t)+
˜
A|
Ω
2
(c
i,j+1
)
k
(t)
+
˜
B|
Ω
1
(c
i+1,j
)
k
(t)+
˜
B|
Ω
2
(c
i−1,j−1
)
k
(t),
with (c
i,j+1
)
k
(t
n
)=(c
n
)
k
, (5.7)
d(c
i+1,j+1
)
k
(t)
dt
=
˜
A|
Ω
1
(c
i,j
)
k
(t)+
˜
A|
Ω
2
(c
i,j+1
)
k
(t)
+
˜
B|
Ω
1
(c
i+1,j
)
k
(t)+
˜
B|
Ω
2
(c
i+1,j+1
)
k
(t),
with (c
i+1,j+1
)
k
(t
n
)=(c
n
)
k
, (5.8)
where c
n
is the known split approximation at the time level t = t
n
,cf. [70].
For the one-dimensional problem, the operators in the equations with the
variable (c
i,j
)
k
above are given as
˜
A|
Ω
1
(c
i,j
)
k
=
$
Ac
i,j
, for k ∈{0,...,p/2}
0 , for k ∈{p/2+1,...,p}
, (5.9)
˜
A|
Ω
2
(c
i,j
)
k
=
$
0 , for k ∈{0,...,p/2 − 1}
Ac
i,j
, for k ∈{p/2,...,p}
, (5.10)
where p/2 is the intermediate point at the overlap.
The assignments for the operator B are similar:
˜
B|
Ω
1
(c
i,j
)
k
=
$
Bc
i,j
, for k ∈{0,...,p/2}
0 , for k ∈{p/2+1,...,p}
, (5.11)
˜
B|
Ω
2
(c
i,j
)
k
=
$
0 , for k ∈{0,...,p/2 − 1}
Bc
i,j
, for k ∈{p/2,...,p}
, (5.12)
© 2009 by Taylor & Francis Group, LLC

100Decomposition Methods for Differential Equations Theory and Applications
where p/2 is the intermediate point at the overlap.
In the same manner as above, the other operators in (5.5)–(5.8) can also
be defined.
REMARK 5.2 We can also generalize our results for the multidimen-
sional case. In that case, we have a set of intermediate boundary nodes, which
couple the multidimensional domains, see [179].
5.1.2 The Overlapping Spatiotemporal Iterative
Splitting Method
We introduce for the semi-discretization in space the variable k as the node
for the point x
k
, and we have k ∈{0,...,p},wherep is the number of nodes.
We concentrate on the one-dimensional overlapping case. For the overlapping
case we assume Ω
1
∩Ω
2
= ∅. We have the following sets: Ω\Ω
2
= {0,...,p
1
},
Ω
1
∩ Ω
2
= {p
1
+1,...,p
2
− 1} and Ω\Ω
1
= {p
2
,...,p}. We assume that the
nodes of the intermediate boundaries are in the sets
Ω\Ω
2
and Ω\Ω
1
,andwe
can also add these points into the overlapping domain.
© 2009 by Taylor & Francis Group, LLC
Spatial Decomposition Methods 101
Assuming p
1
<p
2
<p, we can derive the following overlapping algorithm:
d(c
i,j
)
k
(t)
dt
=
˜
A|
Ω\Ω
2
(c
i,j
)
k
(t)+
˜
A|
Ω
1
∩Ω
2
(c
i,j
,c
i,j−1
)
k
(t)
+
˜
A|
Ω\Ω
1
(c
i,j−1
)
k
(t)
+
˜
B|
Ω\Ω
2
(c
i−1,j
)
k
(t)+
˜
B|
Ω
1
∩Ω
2
(c
i−1,j
,c
i−1,j−1
)
k
(t)
+
˜
B|
Ω\Ω
1
(c
i−1,j−1
)
k
(t),
with (c
i,j
)
k
(t
n
)=(c
n
)
k
, (5.13)
d(c
i+1,j
)
k
(t)
dt
=
˜
A|
Ω\Ω
2
(c
i,j
)
k
(t)+
˜
A|
Ω
1
∩Ω
2
(c
i,j
,c
i,j−1
)
k
(t)
+
˜
A|
Ω\Ω
1
(c
i,j−1
)
k
(t)
+
˜
B|
Ω\Ω
2
(c
i+1,j
)
k
(t)+
˜
B|
Ω
1
∩Ω
2
(c
i+1,j
,c
i−1,j−1
)
k
(t)
+
˜
B|
Ω\Ω
1
(c
i−1,j−1
)
k
(t),
with (c
i+1,j
)
k
(t
n
)=(c
n
)
k
, (5.14)
d(c
i,j+1
)
k
(t)
dt
=
˜
A|
Ω\Ω
2
(c
i,j
)
k
(t)+
˜
A|
Ω
1
∩Ω
2
(c
i,j+1
,c
i,j
)
k
(t)
+
˜
A|
Ω\Ω
1
(c
i,j+1
)
k
(t)
+
˜
B|
Ω\Ω
2
(c
i+1,j
)
k
(t)+
˜
B|
Ω
1
∩Ω
2
(c
i+1,j
,c
i−1,j−1
)
k
(t)
+
˜
B|
Ω\Ω
1
(c
i−1,j−1
)
k
(t),
with (c
i,j+1
)
k
(t
n
)=(c
n
)
k
, (5.15)
d(c
i+1,j+1
)
k
(t)
dt
=
˜
A|
Ω\Ω
2
(c
i,j
)
k
(t)+
˜
A|
Ω
1
∩Ω
2
(c
i,j+1
,c
i,j
)
k
(t)
+
˜
A|
Ω\Ω
1
(c
i,j+1
)
k
(t)
+
˜
B|
Ω\Ω
2
(c
i+1,j
)
k
(t)+
˜
B|
Ω
1
∩Ω
2
(c
i+1,j
,c
i+1,j+1
)
k
(t)
+
˜
B|
Ω\Ω
1
(c
i+1,j+1
)
k
(t),
with (c
i+1,j+1
)
k
(t
n
)=(c
n
)
k
, (5.16)
where c
n
is the known split approximation at the time level t = t
n
W
e have the following operators:
˜
A|
Ω\Ω
2
(c
i,j
)
k
=
$
A(c
i,j
)
k
, for k ∈{0,...,p
1
}
0 , for k ∈{p
1
+1,...,p}
, (5.17)
© 2009 by Taylor & Francis Group, LLC
,cf. [70].

102Decomposition Methods for Differential Equations Theory and Applications
˜
A|
Ω
1
∩Ω
2
(c
i,j
,c
i,j+1
)
k
=
⎧
⎨
⎩
0 , for k ∈{0,...,p
1
− 1}
A((c
i,j
+ c
i,j+1
)/2)
k
, for k ∈{p
1
,...,p
2
}
0 , for k ∈{p
2
+1,...,p}
,
(5.18)
˜
A|
Ω\Ω
1
(c
i,j
)
k
=
$
0 , for k ∈{0,...,p
2
− 1}
A(c
i,j
)
k
, for k ∈{p
2
,...,p}
. (5.19)
The assignments are similar for the operator B.
˜
B|
Ω\Ω
2
(c
i,j
)
k
=
$
B(c
i,j
)
k
, for k ∈{0,...,p
1
}
0 , for k ∈{p
1
+1,...,p}
, (5.20)
˜
B|
Ω
1
∩Ω
2
(c
i,j
,c
i,j+1
)
k
=
⎧
⎨
⎩
0 , for k ∈{0,...,p
1
− 1}
B((c
i,j
+ c
i,j+1
)/2)
k
, for k ∈{p
1
,...,p
2
}
0 , for k ∈{p
2
+1,...,p}
,
(5.21)
˜
B|
Ω\Ω
1
(c
i,j
)
k
=
$
0 , for k ∈{0,...,p
2
− 1}
B(c
i,j
)
k
, for k ∈{p
2
,...,p}
. (5.22)
In the same manner as above, the other operators in (5.13)–(5.16) can be
defined.
REMARK 5.3 We can generalize our results for the multidimensional
case. The overlapping case is a set of the overlapping domain that couples
the multidimensional domains, see [179].
5.1.3 Error Analysis and Convergence of the
Combined Method
THEOREM 5.1
Let us consider the linear operator equation in a Banach space X:
dc(t)
dt
= A
1
c(t)+A
2
c(t)+B
1
c(t)+B
2
c(t), 0 <t≤ T,
c(0) = c
0
,
where A
1
,A
2
,B
1
,B
2
,A
1
+ A
2
+ B
1
+ B
2
: X → X are given linear operators
being generators of the C
0
semigroup and c
0
∈ X is a given element. Then
the iteration process (5.1)–(5.4) is convergent with a convergence rate of one.
© 2009 by Taylor & Francis Group, LLC

Spatial Decomposition Methods 103
We obtain the iterative result: e
i,j
(t)≤Kτ
n
e
i−1,j−1
(t) + O (τ
2
n
),where
τ
n
= t
n+1
− t
n
and t ∈ [t
n
,t
n+1
].
PROOF
Let us consider the iteration (5.1)–(5.4) on the subinterval [t
n
,t
n+1
]. We
consider the case of the exact initial conditions given as c
i,j
(t
n
)=c
i+1,j
(t
n
)=
c
i,j+1
(t
n
)=c
i+1,j+1
(t
n
)=c(t
n
), where a generalization is also possible. For
the error functions e
i,j
(t):=c(t) − c
i,j
(t), we have the relations
de
i,j
(t)
dt
= A
1
e
i,j
(t)+A
2
e
i,j−1
(t)+B
1
e
i−1,j
(t)+B
2
e
i−1,j−1
(t),
e
i,j
(t
n
)=0, (5.23)
de
i+1,j
(t)
dt
= A
1
e
i,j
(t)+A
2
e
i,j−1
(t)+B
1
e
i+1,j
(t)+B
2
e
i−1,j−1
(t),
e
i+1,j
(t
n
)=0, (5.24)
de
i,j+1
(t)
dt
= A
1
e
i,j
(t)+A
2
e
i,j+1
(t)+B
1
e
i+1,j
(t)+B
2
e
i−1,j−1
(t),
e
i,j+1
(t
n
)=0, (5.25)
de
i,j
(t)
dt
= A
1
e
i,j
(t)+A
2
e
i,j+1
(t)+B
1
e
i+1,j
(t)+B
2
e
i+1,j+1
(t),
e
i,j
(t
n
)=0, (5.26)
for t ∈ [t
n
,t
n+1
], i, j =1, 3, 5,...,withe
1,1
(0) = 0 and e
1,0
(t)=e
0,1
(t)=
e
0,0
(t)=c(t).
Here we use the notation X
4
for the product space Π
4
i=1
X enabled with
the norm (u
1
,u
2
,u
3
,u
4
)
T
=max
i=1,...,4
{u
i
} (u
i
∈ X,i=1,...,4),
and for each component we apply the supremum norm. The elements E
i
(t),
F
i
(t) ∈ X
4
and the linear operator A : X
4
→ X
4
are defined as follows:
E
i,j
(t)=
⎡
⎢
⎢
⎣
e
i,j
(t)
e
i+1,j
(t)
e
i,j+1
(t)
e
i+1,j+1
(t)
⎤
⎥
⎥
⎦
, A =
⎡
⎢
⎢
⎣
A
1
000
A
1
B
1
00
A
1
B
1
A
2
0
A
1
B
1
A
2
B
2
⎤
⎥
⎥
⎦
,
F
i,j
(t)=
⎡
⎢
⎢
⎣
A
2
e
i,j−1
(t)+B
1
e
i−1,j
(t)+B
2
e
i−1,j−1
(t)
A
2
e
i,j−1
(t)+B
2
e
i−1,j−1
(t)
B
2
e
i−1,j−1
(t)
0
⎤
⎥
⎥
⎦
. (5.27)
Using the notations (5.27), the relations (5.23)–(5.26) can be written in the
following form:
dE
i,j
(t)
dt
= AE
i,j
(t)+F
i,j
(t),t∈ [t
n
,t
n+1
],
E
i,j
(t
n
)=0.
(5.28)
© 2009 by Taylor & Francis Group, LLC

104Decomposition Methods for Differential Equations Theory and Applications
We estimate the right-hand side F
i,j
(t) in the following lemma:
LEMMA 5.1
For F
i,j
(t)itholds
||F
i,j
(t)|| ≤ C||e
i−1,j−1
(t)||.
PROOF
We have the following norm
||F
i,j
(t)|| =max{||F
i,j,1
(t)||, ||F
i,j,2
(t)||, ||F
i,j,3
(t)||, ||F
i,j,4
(t)||}.
Each term can be estimated as
||F
i,j,1
(t)|| = ||A
2
e
i,j−1
(t)+B
1
e
i−1,j
(t)+B
2
e
i−1,j−1
(t)|| ≤ C
1
||e
i−1,j−1
(t)||,
||F
i,j,2
(t)|| = ||A
2
e
i,j−1
(t)+B
2
e
i−1,j−1
(t)|| ≤ C
2
||e
i−1,j−1
(t)||,
||F
i,j,3
(t)|| = ||B
2
e
i−1,j−1
(t)|| ≤ C
3
||e
i−1,j−1
(t)||.
Based on the theorem of Fubini for decouplable operators, see [43], we obtain
||e
˜
i
,
˜
j
(t)|| ≤ ||e
i−1,j−1
||,for
˜
i = {i − 1,i} and
˜
j = {j − 1,j} .
Hence, it holds that
||F
i,j
(t)|| ≤ C||e
i−1,j−1
(t)||,
where C is the maximum value of C
1
, C
2
and C
3
.
Using the variations of constants formula, the solution of the abstract
Cauchy problem (5.28) with homogeneous initial conditions can be written
as
E
i,j
(t)=
t
t
n
exp(A(t − s))F
i,j
(s)ds, t ∈ [t
n
,t
n+1
].
(See, e.g., [63].) Hence, using the denotation
F
i,j
∞
=sup
t∈[t
n
,t
n+1
]
F
i,j
(t),
and taking into account Lemma 5.1, we have
E
i,j
(t)≤F
i,j
∞
t
t
n
exp(A(t − s))ds
≤ C e
i−1,j−1
(t)
t
t
n
exp(A(t − s))ds, t ∈ [t
n
,t
n+1
].
(5.29)
© 2009 by Taylor & Francis Group, LLC
Spatial Decomposition Methods 105
Due to our linearity assumptions for the operators, A is a generator of the
one-parameter C
0
semigroup (A(t))
t≥0
. Because (A(t))
t≥0
is a semigroup,
the growth estimation
exp(At)≤
%
K exp(ωt),t≥ 0 ,
(5.30)
holds with some numbers
%
K ≥ 0andω ∈ R,see[63].
• Assume that (A(t))
t≥0
is a bounded or exponentially stable semigroup
that is, (5.30) holds for some ω ≤ 0. Then it is apparent that the
estimate
exp(At)≤
%
K, t ≥ 0,
holds, and considering (5.29), we have the relation
E
i,j
(t)≤Kτ
n
e
i−1,j−1
(t),t∈ [t
n
,t
n+1
].
(5.31)
• Assume that (A(t))
t≥0
has an exponential growth with some ω>0.
Integrating (5.30) yields
t
t
n
exp(A(t − s))ds ≤ K
ω
(t),t∈ [t
n
,t
n+1
],
(5.32)
where
K
ω
(t)=
%
K
ω
(exp(ω(t − t
n
)) − 1) ,t∈ [t
n
,t
n+1
],
and hence,
K
ω
(t) ≤
%
K
ω
(exp(ωτ
n
) − 1) =
%
Kτ
n
+ O(τ
2
n
),
(5.33)
with τ
n
= t
n+1
− t
n
.
The estimations (5.29), (5.30), and (5.33) result in
E
i,j
(t)≤Kτ
n
e
i−1,j−1
(t) + O(τ
2
n
),
where K =
%
K · C for both cases.
Taking into account the definition of E
i,j
(t)andthenorm·,weobtain
e
i,j
(t)≤Kτ
n
e
i−1,j−1
(t)+ O(τ
2
n
),
which proves our statement.
© 2009 by Taylor & Francis Group, LLC
