Geiser J. Decomposition Methods for Differential Equations: Theory and Applications

Подождите немного. Документ загружается.

86Decomposition Methods for Diﬀerential Equations Theory and Applications

I−τ

4,θ

we derive

((I−τ

4,θ

)∂

∂

−

j,k

,∂

j,k

)τ

((I−τ

4,θ

)(∂

− ∂

−

j,k

, (∂

+ ∂

−

j,k

)





(I−τ

4,θ

)(∂

− ∂

−

)



(∂

+ ∂

−

j,k

≤ (1 − τ

˜ω)



(∂

j,k

)

(∂

−

j,k

)

dx, (4.48)

where the operator I−τ

4,θ

is symmetric and positive deﬁnite, and we can

apply the weighted norm, see Remark 4.7 and [65].

We obtain the following result:

(1 − τ

˜ω)



(∂

j,k

)

(∂

−

j,k

)

dx (4.49)

=1/2||(1 − τ

˜ω)

1/2

∂

j,k

−1/2||(1 − τ

˜ω)

1/2

∂

−

j,k

. (4.50)

For −M

, we ﬁnd

(−M

(θU

n+1

j,k

− (1 − 2θ)U

j,k

+ θU

n−1

j,k

),∂

j,k

)τ

=1/2(P

j,k

,θ) −P

−

j,k

,θ)). (4.51)

As a result of the operators P

−

j,k

,θ)=P

n−1

j,k

,θ)and∂

−

j,k

= ∂

n−1

j,k

we can recursively derive the following result:

||(1 − τ

˜ω)

1/2

∂

j,k

+ P

j,k

,θ) ≤||(1 − τ

˜ω)

1/2

∂

j,k

+ P

j,k

,θ), (4.52)

where for θ ∈ [0.25, 0.5] we ﬁnd P

j,k

,θ) ≥ 0 for all N ∈ N

, and, therefore,

we have the unconditional stability. The scalar proof is also presented in the

work of [133].

REMARK 4.8 For θ =

, the splitting method is fourth-order ac-

curate in time and space; see the following theorem.

THEOREM 4.6

We obtain a fourth-order accurate scheme in time and space for the splitting

method, see (4.35)–(4.37),whenθ =1/12. We ﬁnd

∂

−

j,k

− 1/12M

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

)+M

j,k

4,θ

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

)=(0, 0)

, (4.53)

Decomposition Methods for Hyperbolic Equations 87

where M

is a fourth-order discretization scheme in space.

PROOF

We consider the following Taylor expansion:

∂

j,k

= ∂

∂

−

j,k

−

∂

tttt

j,k

+ O(τ

). (4.54)

Furthermore, we have

∂

tttt

j,k

≈M

∂

j,k

, (4.55)

and we can rewrite (4.54) as

∂

j,k

≈ ∂

∂

−

j,k

−

∂

j,k

+ O(τ

)

≈ ∂

∂

−

j,k

−

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

)+O(τ

). (4.56)

The fourth-order time-stepping algorithm can be formulated as

∂

−

j,k

−

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

) −M

j,k

=(0, 0)

. (4.57)

The splitting method, (4.35)–(4.37), becomes

∂

−

j,k

−

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

) −M

j,k

−N

n+1

j,k

− 2U

j,k

+ U

n−1

j,k

)=(0, 0)

, (4.58)

and we obtain a fourth-order split scheme, cf. the scalar case [133].

REMARK 4.9 From Theorem 4.6 we ﬁnd that the splitting method

is fourth order in time for θ =1/12. For the stability analysis, the method is

conditionally stable for θ ∈ (0, 0.25). So the splitting method will not restrict

our stability condition for the fourth-order method with θ =1/12.

To improve the time-step behavior, we introduce the iterative operator-

splitting methods for hyperbolic equations.

4.3 Iterative Operator-Splitting Methods for Wave

Equations

In the following, we present the iterative operator-splitting method as an

extension of the traditional splitting method for wave equations.

88Decomposition Methods for Diﬀerential Equations Theory and Applications

Our objective is to repeat the splitting steps with the improved computed

solutions. We solve a ﬁxed-point iteration and we obtain higher-order results.

The iterative splitting method is given in the continuous formulation

(t)

= Ac

(t)+Bc

i−1

(t)+f(t),t∈ [t

n+1

with c

)=c

)

, (4.59)

i+1

(t)

= Ac

(t)+Bc

i+1

(t)+f(t),t∈ [t

n+1

with c

i+1

)=c

i+1

)

, (4.60)

where c

(t),

(t)

are ﬁxed functions for each iteration. (Here, as before,

denote known split approximations at the time level t = t

.) The

time-step is given as τ = t

n+1

−t

. The split approximation at the time level

t = t

n+1

is c

n+1

= c

2m+1

n+1

For the discrete version of the iterative operator-splitting method, we apply

the second-order discretization of the time derivations and obtain

− 2c(t

)+c(t

n−1

)=τ

A(ηc

+(1− 2η)c(t

)+ηc(t

n−1

)) (4.61)

+τ

B(ηc

i−1

+(1− 2η)c(t

)+ηc(t

n−1

))

+τ

(ηf(t

n+1

)+(1− 2η)f(t

)+ηf(t

n−1

)),

i+1

− 2c(t

)+c(t

n−1

)=τ

A(ηc

+(1− 2η)c(t

)+ηc(t

n−1

)) (4.62)

+τ

B(ηc

i+1

+(1− 2η)c(t

)+ηc(t

n−1

))

+τ

(ηf(t

n+1

)+(1− 2η)f(t

)+ηf(t

n−1

)),

where we iterate for i =1, 3, 5,...and the starting solution c

(t),

(t)

are any

ﬁxed function for each iteration, for example, c

(t)=

(t)

=0. Theresult

is given as c(t

n+1

) with the initial conditions c(t

)=c

and

dc(t

)

and η ∈ [0, 0.5], using the fully coupled method for η = 0 and the decoupled

method for 0 <η≤ 0.5, which is a mixing of explicit and implicit Euler

methods.

REMARK 4.10 The stop criterion is given as |c

k+1

−c

|≤,where

k ∈ 1, 3, 5,... and  ∈ R

Therefore, the solution is given as c(t

n+1

) ≈ c

k+1

n+1

)=c

n+1

For the stability and consistency, we can rewrite Equations (4.61)–(4.62) in

the continuous form in the operator equation as

= AC

+ F

, (4.63)

Decomposition Methods for Hyperbolic Equations 89

where C

=(c

i+1

)

, and the operators are given as

A =



A 0



, F



i−1



. (4.64)

This equation is discussed in the following cases, in which the results are given

with respect to stability and consistency.

4.3.1 Stability and Consistency Theory for the Iterative

Operator-Splitting Method

The stability and consistency results can be obtained as we saw for the

parabolic case. The operator equation with second-order time derivatives can

be reformulated as a system of ﬁrst-order time derivatives.

4.3.1.1 Consistency for the Iterative Operator-Splitting Method

for Wave Equations

We now analyze the consistency and order of the local splitting error for

the linear bounded operators A, B : X → X,whereX is a Banach space, see

[200].

WeassumeourCauchyproblemfortwolinearoperatorsforthesecond-

order time derivative:

− Ac − Bc =0, for t ∈ (0,T), (4.65)

with c(0) = c

dc(0)

= c

, (4.66)

where c

and c

are the initial values, see Section 2.2.3.

We rewrite to a system of ﬁrst-order time derivatives:

∂

− c

=0, in (0,T), (4.67)

∂

− Ac

− Bc

=0, in (0,T), (4.68)

with c

(0) = c

, (4.69)

where c

= c(0) and c

dc(0)

are the initial values.

The iterative operator-splitting method (4.59)–(4.60) is rewritten to a sys-

tem of splitting methods.

The method is given as

∂

1,i

= c

2,i

, (4.70)

∂

2,i

= Ac

1,i

+ Bc

1,i−1

, (4.71)

with c

1,i

)=c

),c

2,i

)=c

∂

1,i+1

= c

2,i+1

, (4.72)

∂

2,i+1

= Ac

1,i

+ Bc

1,i+1

, (4.73)

with c

1,i+1

)=c

),c

2,i+1

)=c

90Decomposition Methods for Diﬀerential Equations Theory and Applications

We start with i =1, 3, 5,...,2m + 1 and the initial conditions c

), c

)

are the approximate solutions at t = t

We can obtain consistency with the underlying fundamental solution of the

equation system.

THEOREM 4.7

Let A, B ∈L(X) be given linear bounded operators. Then the abstract Cauchy

problem (4.65)–(4.66) has a unique solution, and the iterative splitting method

(4.70)–(4.73) for i =1, 3,...,2m +1 is consistent with the order of the con-

sistency O(τ

The error estimate is given as

e

 = KBτ

e

i−1

 + O(τ

), (4.74)

where e

=max{|e

1,i

|, |e

i,2

|}.

PROOF

We derive the underlying consistency of the operator-splitting method.

Let us consider the iteration (4.61)–(4.62) on the subinterval [t

n+1

]. For

the local error function e

(t)=c(t) − c

(t), we have the relations

∂

1,i

(t)=e

2,i

(t),t∈ [t

n+1

∂

2,i

(t)=Ae

1,i

(t)+Be

1,i−1

(t),t∈ [t

n+1

∂

1,i+1

(t)=e

2,i+1

(t),t∈ [t

n+1

∂

2,i+1

(t)=Ae

1,i

(t)+Be

1,i+1

(t),t∈ [t

n+1

(4.75)

for i =0, 2, 4,...,withe

(0) = 0 and e

−1

(t)=c(t). We use the notation

=Π

i=1

X for the product space, which enables the norm

||(u

)

|| =max{||u

||, ||u

||} with (u

∈ X),

and for each component we assume the supremum norm.

The elements E

(t), F

(t) ∈ X

and the linear operator A : X

→ X

are

deﬁned as

(t)=

⎡

⎢

⎣

1,i

(t)

2,i

(t)

1,i+1

(t)

2,i+1

(t)

⎤

⎥

⎦

, F

(t)=

⎡

⎢

⎣

1,i−1

(t)

⎤

⎥

⎦

, A =

⎡

⎢

⎣

0 I 00

A 000

0 I 0 I

A 0 B 0

⎤

⎥

⎦

. (4.76)

Then, using the notations (4.76), the relations of (4.75) can be written:

∂

(t)=AE

(t)+F

(t),t∈ (t

n+1

)=0.

(4.77)

Due to our assumptions, A is a generator of the one-parameter C

semigroup

(exp At)

t≥0

; hence, using the variations of constants formula, the solution to

Decomposition Methods for Hyperbolic Equations 91

the abstract Cauchy problem (4.77) with homogeneous initial conditions can

be written as

(t)=c



exp(A(t − s))F

(s)ds,

(4.78)

with t ∈ [t

n+1

]. (See, e.g., [63].) Hence, using the denotation

E



∞

=sup

t∈[t

n+1

]

E

(t),

(4.79)

we have

E

(t) ≤F



∞



exp(A(t − s))ds

= Be

1,i−1





exp(A(t − s))ds, t ∈ [t

n+1

(4.80)

Because (A(t))

t≥0

is a semigroup, the growth estimation

exp(At)≤K exp(ωt),t≥ 0,

(4.81)

holds for some numbers K ≥ 0andω ∈ R,cf.[63].

The estimations (4.80) and (4.81) result in

E



∞

= K Bτ

e

i−1

 + O(τ

(4.82)

where ||e

i−1

|| =max{||e

1,i−1

||, ||e

2,i−1

||}.

Taking into account the deﬁnition of E

and the norm ·

∞

,weobtain

e

 = KBτ

e

i−1

 + O(τ

(4.83)

and hence,

e

i+1

 = K

e

i−1

 + O(τ

), (4.84)

which proves our statement.

REMARK 4.11 The proof is aligned to scalar temporal ﬁrst-order

derivatives, see [70]. The generalization can also be extended to higher-order

hyperbolic equations, which are reformulated in ﬁrst-order systems.

4.3.1.2 Stability for the Iterative Operator-Splitting Method for

Wave Equations

The following stability theorem is given for the wave equation performed

with the iterative splitting method, see (4.70)–(4.73).

The convergence is examined in a general Banach space setting, and we can

prove the following stability theorem.

92Decomposition Methods for Diﬀerential Equations Theory and Applications

THEOREM 4.8

Let us consider the system of linear diﬀerential equations used for the spatial

discretized wave equation:

= c

, (4.85)

= Ac

+ Bc

, (4.86)

with c

)=c(t

),c

dc(t

)

where the operators A, B : X → X are linear and densely deﬁned in the real

Banach space X,see[201] and Section 3.2.4. We can deﬁne a norm on the

product space X × X with ||(u, v)

|| =max{||u||, ||v||}.

We rewrite the equations (4.85)–(4.86) and obtain

d˜c(t)

A˜c(t)+

B˜c(t),

˜c(t

)=˜c

(4.87)

where ˜c

=(c(t

dc(t

)

A =



01/2I

A 0



and

B =



01/2I

B 0



We assume that

B : X

→ X

are given linear bounded operators that

generate the C

semigroup, and ˜c, ˜c

∈ X

are given elements.

We also assume λ

is an eigenvalue of

A and λ

is an eigenvalue of

Then the linear iterative operator-splitting method for wave equations (4.70)–

(4.73) is stable with the following result:

˜c

i+1

n+1

)≤



i+1

j=0

˜c

τ

max

(4.88)

where

K>0 is a constant and ˜c

=(c(t

dc(t

)

is the initial condition,

τ =(t

n+1

− t

) is the time-step, and λ

max

is the maximal eigenvalue of the

linear and bounded operators

A and

We discuss Theorem 4.8 in the following proof.

PROOF

Let us consider the iteration (4.70)–(4.73) on the subinterval [t

n+1

Then we obtain the eigenvalues of the following linear and bounded oper-

ators. Because of the well-posed problem, we have λ

eigenvalue of

A, λ

eigenvalue of

B, see [125] and [201].

Then our iteration methods are given with the eigenvalues as follows:

∂

˜c

(t)=λ

˜c

(t)) + λ

˜c

i−1

(t),t∈ (t

n+1

˜c

)=˜c

(4.89)

Decomposition Methods for Hyperbolic Equations 93

and

∂

˜c

i+1

(t)=λ

˜c

(t)+λ

˜c

i+1

(t),t∈ (t

n+1

˜c

i+1

)=˜c

(4.90)

for i =1, 3, 5,...,with˜c

=(c(t

dc(t

)

The equations can be estimated with

˜c

n+1

)=exp(λ

τ)˜c



n+1

exp(λ

n+1

− s))λ

˜c

i−1

(s)ds, (4.91)

where we can estimate the result as

||˜c

n+1

)|| ≤ K

||˜c

||+ τK

||˜c

i−1

n+1

)||. (4.92)

where K

, K

are the growth estimates for the exp-functions, see Section

4.3.1.1, and we neglect the higher-order terms.

We can also estimate the second equation:

˜c

i+1

n+1

)=exp(λ

τ)˜c



n+1

exp(λ

n+1

− s))λ

˜c

(s)ds, (4.93)

which can be estimated as

||˜c

i+1

n+1

)|| ≤ K

||˜c

||+ τK

||˜c

n+1

)||. (4.94)

where K

, K

are the growth estimates for the exp-functions, see Section

4.3.1.1, and we neglect the higher-order terms.

With the recursive argument and the maximum of the eigenvalues, we can

estimate the equations:

||˜c

i+1

n+1

)|| ≤ ||˜c

i+1



j=0

max

, (4.95)

||˜c

i+1

n+1

)|| ≤

K ||˜c

i+1



j=0

max

, (4.96)

where

K is the maximum of all constants and λ

max

=max{λ

,λ

REMARK 4.12 We have stability for suﬃcient small time-steps τ.

Based on the estimation with the eigenvalues, we can do the same technique

for unbounded operators that are boundable in a sector. In addition, accurate

estimates can be derived using the techniques of the mild or weak solutions,

see [201].

94Decomposition Methods for Diﬀerential Equations Theory and Applications

Processor 1 Processor 2 Processor 3

tttttt

n+4 n+7 n+11 n+15 n+19

Window 1

Window 2

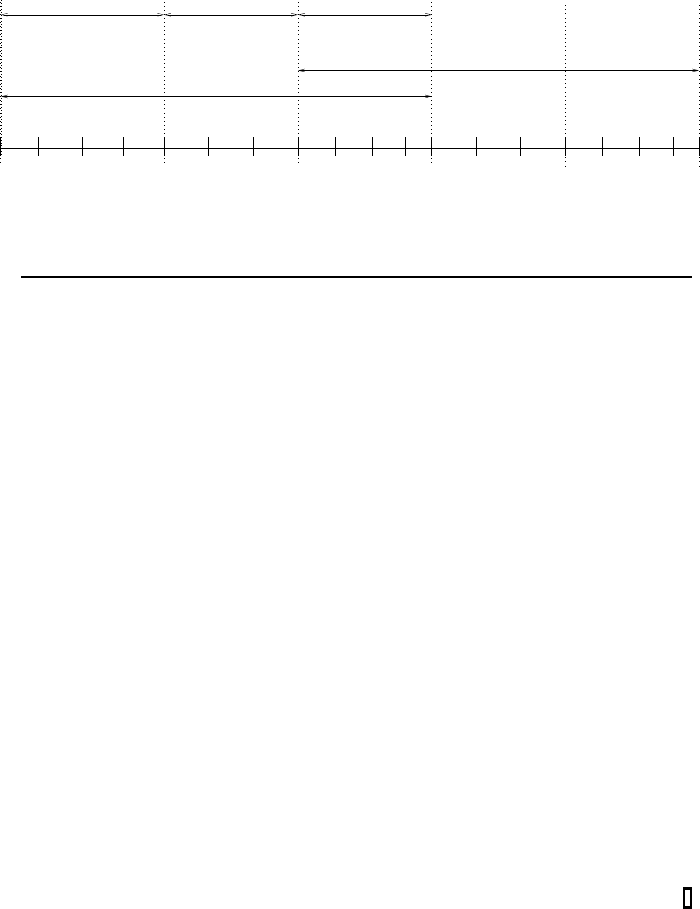
FIGURE 4.2: Parallelization of the time intervals.

4.4 Parallelization of Time Decomposition Methods

The parallelization of the splitting methods is suited in applications for

CFD or convection-diﬀusion-reaction processes and large-scale computations.

We present two possible parallelization techniques:

1) Windowing (see [194]);

2) Block-wise clustering (see [35] and [36]).

4.4.1 Windowing

The ﬁrst direction is the parallelization of the time-stepping process. A large

time-step is decoupled into smaller time-steps and is solved independently with

higher-order time discretization methods by any processor. The core concept

of parallelization is windowing, in which the processor has one or more time-

steps to compute and shares the end result of the computation as an initial

condition for the next processor.

A graphical visualization of such a parallelization technique is presented in

Figure 4.2.

REMARK 4.13 The windowing technique is eﬃcient for our itera-

tive splitting methods, because they can be parallelized on the global level.

Therefore, in each local time partition, the processors solve the local operator

equation and the communication is done on the global level to forward the

initial solutions for the next time partition.

4.4.2 Block-Wise Clustering

A further parallelization of the methods is the block-wise decoupling of the

matrix into simpler solvable partitions. In this technique, we parallelize on

each operator level. Therefore, the parallelization is based on solving each

submatrix independently and summarizing the results in an additional step

Decomposition Methods for Hyperbolic Equations 95

to get the results.

The local operator equations are given as a system of ﬁrst-order diﬀerential

equations:

= Au, for t ∈ [0,T],

+ A

≈ A, (4.97)

u(0) = u

where the matrices are given as

A =

⎛

⎜

⎝

··· A

n−1n

··· A

nn−1

⎞

⎟

⎠

, (4.98)

and the entries are denoted as A

>> A

, ∀ i, j =1,...,n and i = j (i.e.,

diagonal dominant matrices).

We assume that the outer diagonal entries can be neglected, and the addi-

tive operators are given as

+ A

⎛

⎜

⎝

0 ··· 0

0 A

0 ··· 0 A

⎞

⎟

⎠

⎛

⎜

⎝

11,1

0 ··· 0

0 A

22,1

··· 0 A

nn,1

⎞

⎟

⎠

⎛

⎜

⎝

11,2

0 ··· 0

0 A

22,2

0 ··· 0 A

nn,2

⎞

⎟

⎠

. (4.99)

The block-wise clustering allows us to parallelize with respect to each inde-

pendent block.

We can also implement our splitting method on the local operator level with

and A

REMARK 4.14 The block-wise clustering allows a parallelization

on the local level. Therefore, the outer diagonal entries of the underlying

matrices are negligible or very small. The processors can be distributed to

the various blocks to compute the problems independently. These concepts

are also discussed in [35] and [36].