Gebali F. Analysis Of Computer And Communication Networks

Подождите немного. Документ загружается.

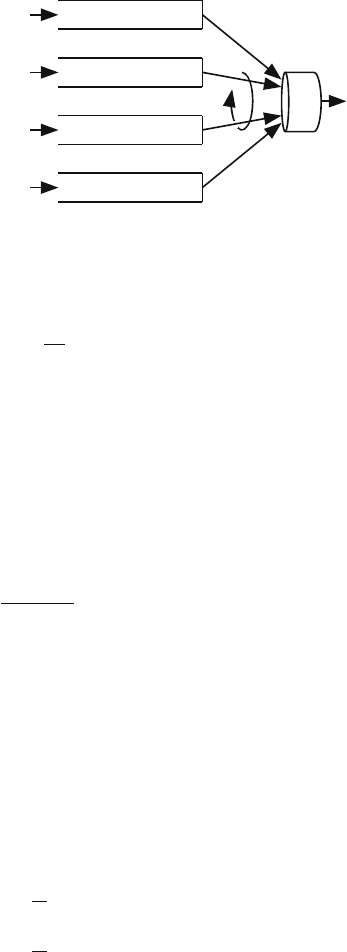
440 12 Scheduling Algorithms

Fig. 12.3 Round robin

scheduler serving four

sessions

Session 1

Scheduler

Session 2

Session 3

Session 4

Assuming m sessions, the maximum bound on delay for a queue is given by

W(max) =



i=1

s (12.3)

where A

is the head of the line packet length in bits for session i and C (bps) is the

output link rate.

The ratio of service provided for session i relative to the total service provided to

all sessions is equivalent to finding the ratio of number of bits moved from session

i relative to the total number of bits moved in one round. We define f

as that ratio

which is written as



j=1

(12.4)

Thus the bandwidth C

given to session i relative to the total output bandwidth is

simply given by

= Cf

(12.5)

In an ideal round robin algorithm, all packets have equal lengths and each session

share would be

(12.6)

(12.7)

The above two equations assume that all sessions are backlogged and have pack-

ets with equal lengths. The algorithm is not fair when some sessions have variable

length packets since the server will allocate more time for these sessions.

12.11 Round Robin Scheduler (RR) 441

12.11.1 Queuing Analysis for RR

We can study the occupancy of each queue in a round robin scheduler using the

following assumptions:

1. The outgoing link capacity is C.

2. The number of queues or sessions is m.

3. The size of queue i is B

4. Time step equals T , the duration of one round of the scheduler.

5. The input data rate for session i is λ

6. The maximum burst rate for queue i is σ

7. The head of line packet length for queue i is A

8. The arrival probability for queue i is a

9. A maximum of N

packets could arrive during one round into queue i.

10. The size of queue i is B

11. The probability of departure from queue i is c

= 1.

Based on the above assumptions, we find that we have an M

/M/1/B queue.

The transition matrix for such queue was derived in Section 7.7 on page 241. Based

on that, we can derive expressions for the scheduling delay, which corresponds to

the queuing delay in that situation.

The arrival probability a

can be found as follows. The duration of one round T

is given by

T =



i=1

s (12.8)

and when all sessions have packets with equal length A, the above expression sim-

plifies to

T =

s (12.9)

The average interarrival time for session i is given by

s (12.10)

The probability of k arrivals in one time step is given by

i,k





−k

k = 0, 1, 2,...,N

(12.11)

where a

is the Bernoulli probability of packet arrival, b

= 1 − a

, and N

is the

maximum number of packets that could arrive at the queue input as determined by

the maximum burst rate σ

442 12 Scheduling Algorithms

× T

(12.12)

with x is the smallest integer that is larger than or equal to x. Assuming binomial

distribution, we can estimate a

from the average number of packets received on one

time step:

× N

× T

(12.13)

which gives

× T

(12.14)

Because of our choice for the step size, the queue size can only decrease by one

at most at any instant with probability c

= 1.

Assuming the packet buffer size B

, the transition matrix for queue i will be

+1) ×(B

+1) and is given by

P =

⎡

⎢

⎣

000··· 0

00··· 0

0 ··· 0

··· 0

−1

−2

−3

−4

··· p

··· f

⎤

⎥

⎦

(12.15)

where q = p

+ p

and

= 1 −

−j+1



k=0

(12.16)

Of course, if B

> N

, then the terms p

= 0 whenever N

< j ≤ p

The transition matrix helps us find performance parameters for queue i. For that,

we need to determine the equilibrium distribution vector s. Repeating the same pro-

cedure for all other queues, we would then be able to find the performance of the

round robin scheduler.

For queue i, the throughput is given by

Th = 1 −s

packets/timestep (12.17)

12.11 Round Robin Scheduler (RR) 443

where s

is the probability that the queue is empty. The throughput in units of pack-

ets/s is given by

Th =

1 −s

packets/s (12.18)

And the throughput in units of bps is given by

Th =

(

1 −s

)

bps (12.19)

The average queue length is given by



j=0

(12.20)

We can invoke Little’s result to estimate the wait time, which is the average num-

ber of time steps a packet spends in the queue before it is served, as

= W ×Th (12.21)

where W is the average number of time steps that a packet spends in the queue:

W =

1 −s

timesteps (12.22)

The wait time in units of seconds is given by

W =

(1 −s

) A

s (12.23)

Example 12.1 Assume a round robin scheduler in which all sessions are identical

with the following parameters:

N = 4 sessions C = 1 Mbps

B = 5 packets L = 1024 bits

λ = 50 kbps σ = 500 kbps

Determine the transition matrix and determine the system performance parame-

ters.

The duration of one round is

T = 4 ×

1024

5 ×10

= 4.1ms

444 12 Scheduling Algorithms

Based on the data burst rate, a maximum of two packets could arrive during

a time period T . The Bernoulli arrival probability at each queue during this time

period is given by

a = 0.1

The transition matrix is 6 ×6:

P =

⎡

⎢

⎣

0.99 0.810000

0.01 0.18 0.81000

00.01 0.18 0.81 0 0

000.01 0.18 0.81 0

0000.01 0.18 0.81

00000.01 0.19

⎤

⎥

⎦

The equilibrium distribution vector is

s =



0.9877 0.0122 0.0002 0 0 0



The throughput of the queue is

Th = 1 −s

= 0.0124 packets/timestep

= 3.0864 kbps

The average queue length is

= 0.0125

The average wait time for a queue is

W = 4.05 ␮s

12.12 Weighted Round Robin Scheduler (WRR)

The round robin scheduler discussed in the previous section treats all connections

equally. When each connection has a different weight, we get the weighted round

robin (WRR) scheduler.

Assume session i has an integer weight w

associated with it. Then in each round

of service, the WRR scheduler transmits w

packets for session i, and so on.

The fraction of the bandwidth for session i in this algorithm can be measured as

the service associated with session i relative to the total service in one round. The

12.12 Weighted Round Robin Scheduler (WRR) 445

service received by the head of the line packet in queue i is simply the number of

bits transmitted:



j=1

(12.24)

In an ideal WRR algorithm, all packets have equal lengths and the share would



j=1

(12.25)

The algorithm is not fair when some sessions have variable length packets since

the server will allocate more time for these sessions.

12.12.1 Queuing Analysis for WRR

We can study the occupancy of each queue in a WRR scheduler using the following

assumptions:

1. The outgoing link capacity is C.

2. The number of queues or sessions is m.

3. The size of queue i is B

4. The weight associated with queue i is w

5. Time step equals T , the duration of one round of the scheduler.

6. The input data rate for session i is λ

7. The maximum burst rate for queue i is σ

8. The head of line packet length for queue i is A

9. The arrival probability for queue i is a

10. A maximum of N

packets could arrive during one round into queue i.

11. A maximum of w

packets could leave during one round from queue i.

12. The probability of departure from queue i is c

= 1.

Based on the above assumptions, we find that we have an M

/1/B queue.

The arrival probability a

can be found by first selecting a time step value. We

choose the time step to be equal to the duration of one round T

T =



i=1

(12.26)

Next, we have to estimate how many packets arrive in one time step from session

i. The average interarrival time for session i is given by

(12.27)

446 12 Scheduling Algorithms

The probability of k arrivals in one time step is given by

i,k





−k

k = 0, 1, 2,...,N

(12.28)

where a

is the Bernoulli probability of packet arrival, b

= 1 − a

, and N

is the

maximum number of packets that could arrive in one time step. N

is determined by

the maximum burst rate σ

as follows

=σ

× T  (12.29)

where the ceiling function x is the smallest integer that is larger than or equal to

x. Assuming binomial distribution, we can estimate a

from the average number of

packets received in one time step:

× N

= λ

× T (12.30)

which gives

× T

(12.31)

Because of our choice for the step size, the queue size can decrease by w

packets

at most at any instant with probability c

= 1.

From the above calculations, we are able to construct a transition matrix for the

queue of session i. Having done that, we are able to obtain expressions for the queue

parameters such as throughput, delay, and average queue length.

12.13 Max–Min Fairness Scheduling

Scheduling deals with the sharing of a resource among several users. However, not

all users have the same demands on the resource. In many cases, not all users require

an equal share of that bandwidth. How should we divide the bandwidth among all

users in a fair manner? One way to do that is to use the max–min policy.

Max–min sharing policy is an iterative technique for fair sharing of the resource.

For example, assume the outgoing link capacity is C and there are m users. Assume

user i requires a bandwidth λ

and the users are sorted such that

≤ λ

≤···≤λ

(12.32)

The allocation of the bandwidth proceeds as follows:

1. Allocate the bandwidth equally among all users C/m.

2. If λ

< C/m, then give user 1 only λ

12.13 Max–Min Fairness Scheduling 447

3. Allocate the remaining bandwidth C − λ

equally among the remaining users

(C − λ

)/(m − 1).

4. If λ

< (C − λ

)/(m − 1), then give user 2 only λ

5. Repeat the procedure until all users have been considered.

Example 12.2 Assume an outgoing link is being shared among five channels. The

system parameters (in units of Mbps) are as follows:

C = 155

= 10

= 20

= 60

= 80

Find the rates assigned to each flow according to the max–min algorithm.

The sum of the flows due to all users is

10 +20 +60 +80 +80 = 250 Mbps

which is larger than the link capacity. The initial fair rate f is given by

f = 155/5 = 31 Mbps

Flow 1 has the minimal rate and is assigned the flow



= min(10, 31) = 10 Mbps

We adjust the link capacity shared among the remaining four users as

C = 155 −10 = 145 Mbps

The fair rate among four remaining users becomes

f = 145/4 = 36.25 Mbps

Flow 2 has minimal rate and is assigned the flow



= min(20, 36.25) = 20 Mbps

We adjust the link capacity shared among the remaining two users as

C = 145 −20 = 125Mbps

448 12 Scheduling Algorithms

The fair rate among three remaining users becomes

f = 125/3 = 41.7 Mbps

Flow 3 has minimal rate and is assigned the flow



= min(60, 41.7) = 41.7 Mbps

We adjust the link capacity shared among the remaining two users as

C = 125 −41.7 = 93.3 Mbps

The fair rate among two remaining users becomes

f = 93.3/2 = 46.7 Mbps

The bandwidths assigned to the flows become



= 10 Mbps



= 20 Mbps



= 41.7 Mbps



= 46.7 Mbps



= 46.7 Mbps

Note that the aggregate assigned rates equal the outgoing link capacity.

12.14 Processor Sharing (PS)

Processor sharing is an ideal work-conserving scheduler that treats each flow like

a fluid model. Data of a given flow is assumed to be infinitely divisible (even at

level smaller than a bit), and all flows are served simultaneously. Processor sharing

provides max–min fair service. However, PS is an ideal solution that is not imple-

mentable in practice. We study it only to provide the background to other practical

algorithms.

Assuming we have m(t) active flows at a given time t, the rate assigned to flow i

is given by

(t) =

m(t)

(12.33)

where C is the outgoing link capacity. Figure 12.4 shows a PS scheduler serving

four queues.

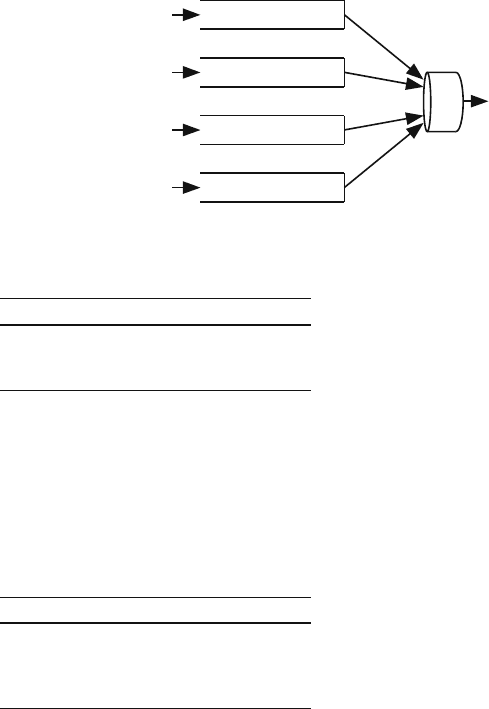
12.15 Generalized Processor Sharing (GPS) 449

Fig. 12.4 Processor sharing

(PS) scheduling in which

each queue shares an equal

portion of server bandwidth

in a fluid flow fashion

Session 1

Scheduler

Session 2

Session 3

Session 4

Example 12.3 Assume a PS scheduler that serves three flows. Packets arrive at the

scheduler according to the following table:

Time 01234

Flow101001

Flow211101

Flow300111

A “0” indicates that the flow is inactive and does not require any output band-

width. A “1” entry indicates an active flow that requires a fair portion of the outgoing

link capacity. For simplicity, we assume discrete time intervals T

, T

, etc. Calculate

the percentage of the outgoing link capacity allocated to each active flow at different

times.

According to PS scheduling, the percentage of the bandwidth dedicated to each

active flow is shown in the following table:

Time 0123 4

Flow10 10 0 1

Flow21 11 0 1

Flow30 01 1 1

% rate 100 50 50 100 33.3

12.15 Generalized Processor Sharing (GPS)

Generalized processor sharing (GPS) is an ideal work-conserving scheduling scheme

that is not implemented in practice. It only helps as a reference to compare the per-

formance of other more practical scheduling algorithm. GPS assumes a fluid flow

traffic model where the scheduler is able to serve an infinitely small amount of data

from each queue at the same time and at different rates.

The bit-by-bit GPS server works on incoming flows in a round robin fashion

transmitting one bit from each flow before it moves on to the next flow. When a

session is idle, the server skips over to the queue of the next session. Therefore, a

single packet requires several rounds of service before it is able to move out of the

scheduler but each packet is guaranteed a fair share of the outgoing link capacity.