Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Н.Б. Введение в математическое моделирование транспортных потоков

Подождите немного. Документ загружается.

128

   











и строгое E-условие (напомним, что







)

     

, , ,

        

    

   

;

 закон сохранения с диффузией (20) имеет двухпараметриче-

ское семейство асимптотически автомодельных решений

(при подстановке такого автомодельного «решения» в урав-

нение (20) почти всюду возникает невязка (в нашем случае

 

1 t

), которая стремится к нулю с ростом времени) вида

волны разрежения (16) тогда и только тогда, когда

 







при

 

  





, за исключением, быть может, конечного

числа точек, в которых имеет место равенство.

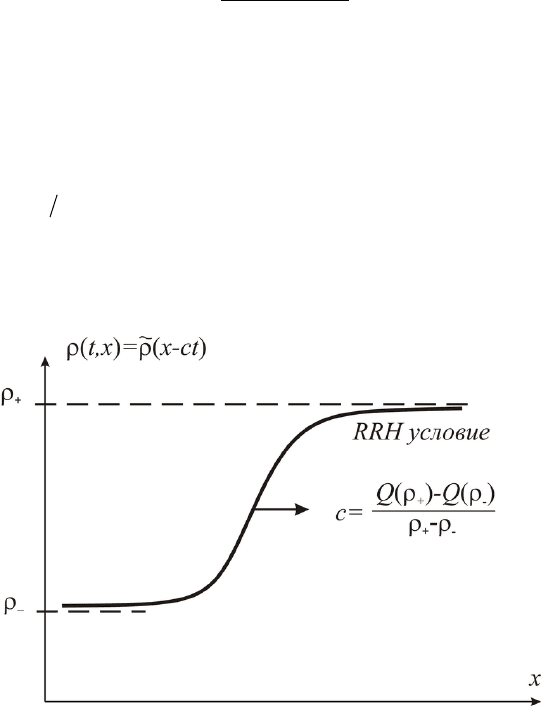
Рис. 19. Бегущая волна

Заметим, что для доказательства всех приведенных утверждений отно-

сительно бегущей волны достаточно рассмотреть краевую задачу для

обыкновенного дифференциального уравнения с разделяющимися пе-

ременными, которое получается при подстановке

 

x ct x









129

в (20) и интегрировании возникшего уравнения с учетом одного из

краевых условий

 

lim













 

   

 

Q s c s Q c D s



  



     



   



  

Заметим также, что RRH-условие получается из оставшегося краевого

условия

 

lim













А строгое E-условие равносильно требованию отсутствия (за исключе-

нием

s  

) особых точек (точек, в которых

 











) у этого обык-

новенного дифференциального уравнения, что в свою очередь равно-

сильно условию

 









(поскольку







Если же допустить существование особой точки

 

,s   

то интеграл

   

 

Q c Q c d

  

    





  



  

будет иметь неинтегрируемую особенность в точке

 









Отсюда следует, что

s 

или

s  

Пришли к противоречию с предположением

 

,s   

Теперь можно объяснить уже анонсированную возможность

обоснования RRH-условия и E-условия на разрывах обобщенных реше-

ний уравнения (13) с помощью метода исчезающей вязкости:

 

x ct x

























   













Упражнение* (см. [19, 28]). Почему строгое E-условие «перехо-

дит в пределе» при





просто в E-условие?

Замечание (модель Лайтхилла–Уизема–Кортевега–де Фриза–

Бюргерса). Если, подобно модели Уизема (см. п. 2.1.3), положить

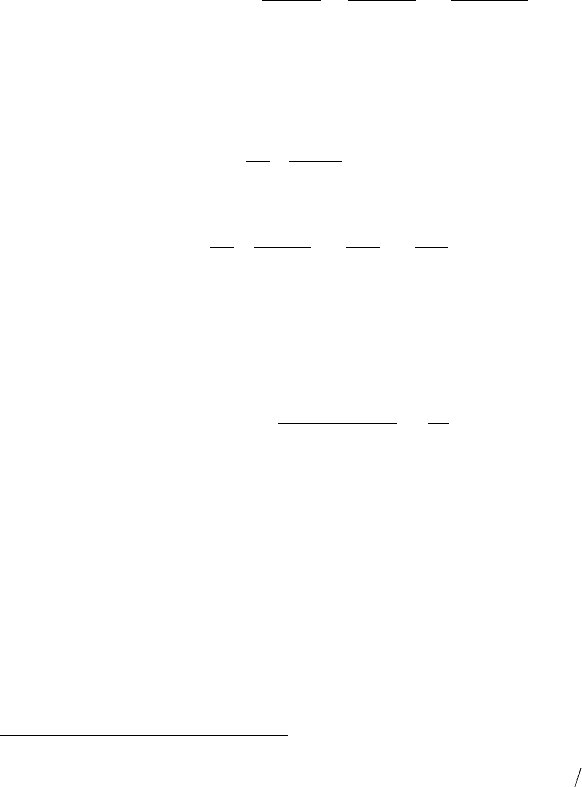
130

   

 

   

v , ,

t x t x

t x V t x

t x x



  







  







где

 

,V t x



– желаемая скорость при данной плотности, а

выражение в скобке описывает «дальнозоркость» водителей (поэтому









), то получим, с учѐтом закона сохранения количества АТС:

 









уравнение типа Кортевега–де Фриза (Вриза)–Бюргерса (КдФБ):

 



  





  

  



. (21)

Поскольку предложенная модель описывает то же самое явление, что и

модель Уизема, то мы вправе надеяться на структурную схожесть авто-

модельных решений уравнений (20) и (21). Действительно, предполо-

жим, что выполняется строгое E-условие, а скорость

определяется

формулой RRH. Тогда (см. [138]) если

 

   

4 sup

  





  





















то существует однопараметрическое семейство строго возрастающих

автомодельных решений уравнения (21) вида бегущей волны

 

x ct x









. Легко показать, что уравнение (21) при

 







 

  





имеет и асимптотическое автомодельное решение вида

волны разрежения (16). Интересно при этом заметить, что в отличие от

уравнения типа Бюргерса для уравнения типа КдФБ обоснование мето-

да исчезающей вязкости и дисперсии – по-прежнему открытая задача

(см. статью П. Лакса в сборнике [30], а также [34, 36]).

Имеет место следующий факт (для простоты формулировки (об-

щий случай изложен в статье [110]) также считаем, что

1kk





Если это условие нарушается, то сначала (когда не сильно нарушается) теряется свойст-

во монотонности бегущей волны (возникают затухающие осцилляции типа

 

sin xx

при

стремлении решения к предельным значениям на краях), а затем автомодельные решения

вида бегущей волны вообще перестают существовать. Численное подтверждение этих

фактов имеется в работах А. Г. Куликовского с коллегами (см., например, [54, 145] и ци-

тированную там литературу). Аналитические исследования, подтверждающие сказанное

выше, были недавно проведены А. В Казейкиной (Вестник МГУ, серия 15. Вычислитель-

ная математика и математическая кибернетика. 2011. № 1 (в печати)).

131

1,...,kn

(или, что то же самое,

1kk







1,...,kn

)) [14, 90, 92; 102–

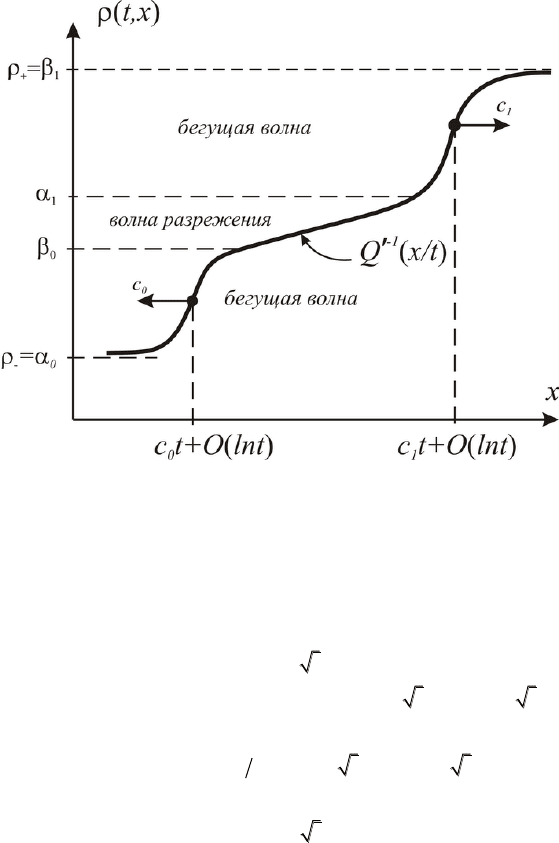
110] (см. рис. 20).

Рис. 20. Система волн

Теорема 2. Существует такой набор функций

 

 

   

ln 1

d t t





   

что решение задачи Коши (20),(15) сходится при

t 

 





(равномерно по

x

) к системе волн

 

 





 

0,..., ,

1,..., ,

k k k k

x c t t

x c t d t c t t x c t t

t x d t

Q x t c t t x c t t

x c t t

















     













   













132

где

 

x c t







– решение уравнения (20) вида бегущей волны с

 

lim









 

lim









Замечание (А. М. Ильин, О. А. Олейник (1960)). Можно пока-

зать (см. [90, 91, 107, 110]), что если

   



  

 







 







то

 

lim

d t d





где

находится из первого интеграла (20) (при

0t 

     

 

0 0 0

; , 0I t d t x x c t d dx







    





Полезной находкой А. М. Ильина и О. А. Олейник стало введение

функции

     

 

w t x t s s c t d ds





   





которая так же, как и

 

,tx



, удовлетворяет уравнению параболическо-

го типа, но при этом

 

lim , 0

w t x





Замечание, аналогичное замечанию Ильина–Олейник, имеет ме-

сто и для теоремы 1.

Замечание (Г. М. Хенкин, А. А. Шананин (2004)). Можно пока-

зать (см. [104–106]), что асимптотические оценки сдвигов фаз

 

 

   

ln 1

d t t





   

«разумно» определять из предложенных в работе [104] «локализован-

ных законов сохранения (первых интегралов)»:

 

   

 

 

; , 0

c t t

k k k k

c t t

I t d t t x x c t d t dx







    





Если приравнять нулю полную производную по времени от

 

;

I t d t

используя уравнение (20), то получим оценку

 

(приняв априорно

за гипотезу, которую апостериорно проверим, что

 

d t t









Точность оценки определяется значениями разностей:

 

t c t t t d t



   



 

x k x k

t c t t t d t



   



133

Эти значения в свою очередь определяются исходя из исследования

сходимости решения к системе волн на участках, соответствующих по-

ведению «волна разрежения». Оказывается, что выбор зависимости

в определении системы волн и в определении локализованных законов

сохранения даѐт наилучшую по точности оценку сдвигов фаз, исходя из

имеющихся способов оценки разностей. В заключение отметим, что при

 





в работах [103; 105–106] были найдены первые (логарифми-

ческие) члены асимптотических рядов для сдвигов фаз. Недавно Г. М.

Хенкиным была высказана гипотеза о том, что следующие члены асим-

птотических рядов будут ограниченными функциями. Пока, насколько

нам известно, не удалось ни доказать, ни опровергнуть эту гипотезу.

Замечание. Можно показать (см. [108–110]), что в теореме 2 ско-

рость сходимости есть

 

1 t

, т.е.

   

 





, , ;

t x t x d t







 







В теореме 1 (см. [35, 90, 95, 96]) скорость сходимости в равномерной

норме (за вычетом сколь угодно малых, но фиксированных на момент

рассмотрения окрестностей ударных волн решения) есть

 

1 t

, при-

чѐм эта оценка неулучшаема [90] и достигается на асимптотике вида

волны разрежения.

Упражнение** (см. п. 2.1.3). При каких условиях уравнение (20)

линеаризуется? Попробуйте построить асимптотические ряды для

 

в этих (частных) случаях. Подобно тому, как это было сделано в

работе [14] (см. также [7]) для уравнения Бюргерса (в случае общих на-

чальных условий см. [103]).

Замечание. Ввиду замечания, касающегося модели Лайтхилла–

Уизема–Кортевега–де Фриза–Бюргерса (см. выше), можно ожидать, что

результат, аналогичный теореме 2, имеет место и для задачи Коши (21),

(15), если только



достаточно мало (насколько мало, зависит как

от функции

 



, так и от начального условия (15)). Для случая, когда

Несложно показать (см. [90]), рассмотрев случай сходимости к одной волне разрежения,

что имеет место сходимость не быстрее

1 t

. Однако пока в общем случае (при отсут-

ствии прилипания) не доказано (и не опровергнуто), что скорость сходимости в теореме 2

оценивается как

 

1 t

134

 



– вогнутая парабола, локальная сходимость к одному из предста-

вителей однопараметрического семейства бегущих волн (параметр –

сдвиг фазы, определяется аналогично замечанию Ильина–Олейник) бы-

ла установлена П. И. Наумкиным и И. А. Шишмарѐвым (1991) [139,

140]. Этот результат недавно был перенесен А. В. Казейкиной (при уча-

стии А. А. Шананина) на произвольную вогнутую функцию [141]. Для

случая, когда

 



– выпуклая функция, глобальная сходимость к вол-

не разрежения была установлена Р. Дуанем и Х. Чжао (2007) [142].

Замечание. Интересно также заметить, что все сказанное выше

относительно модели Уизема в точности (та же структура асимптотики,

те же самые скорости бегущих волн, та же асимптотика у сдвигов фаз

   

d t t

) переносится и на модель Ньюэлла (подробности см. в

[97–107]). Для модели Пэйна получено (см., например, [7]) условие су-

ществования автомодельного решения вида «бегущей – ударной вол-

ны». Оказывается, что скорость такой волны будет удовлетворять фор-

муле RRH.

Замечание (Т.-П. Лю и др. (1997)). Результаты о сходимости к

бегущей волне и волне разрежения решения начальной задачи Коши

(20), (15) могут быть «перенесены» на начально-краевую задачу для

уравнения (20) (подробности см., например, в [143, 144]).

Приведем в заключение этого пункта схему доказательства тео-

рем 1, 2 и аналогичного утверждения для модели Ньюэлла. Доказатель-

ство основывается на следствиях из принципа максимума для линейных

параболических уравнений (с коэффициентами, зависящими от

 

,tx

)

[37, 38, 136]: на принципе сравнения

   

0, 0,xx







   

,,t x t x





0t 

и на принципе сравнения на фазовой плоскости

             

 

1 2 1 2

0, 0, 0, 0, ,x x x x x x

   

  

      



             

 

1 2 1 2

, , , , ,t x t x t x t x x x

   

  

      

0t 

Эти принципы переносятся и на нелинейные параболические уравнения,

а также на некоторые их дифференциально-разностные (и просто

разностные) аналоги. Идея такого перенесения достаточно простая (и

широко используется в теории параболических уравнений [37, 38],

например, для оценки старших производных неизвестной функции) –

нелинейные коэффициенты при частных производных объявляются

некоторыми функциями независимых переменных (в нашем случае

135

). Далее делаются «априорные» предположения относительно

неизвестной функции (как правило, предположения равномерной

ограниченности неизвестной функции или(и) существования у нее

(равномерно ограниченных) производных). В этих предположениях

коэффициенты при частных производных оказываются «настолько

хорошими» функциями, что к возникшему уравнению (в котором

нелинейные коэффициенты, зависящие от неизвестной функции,

интерпретируются просто как некоторые функции независимых

переменных) применимы принципы сравнения. Затем, уже с помощью

этих принципов, проверяется, что сделанные априорно предположения

выполняются. В этой связи также заметим, что иногда априорные

предположения выбирают единственное решение из множества

возможных. Так, для обычного уравнения теплопроводности априорное

предположение, «что решение начальной задачи Коши (с равномерно

ограниченной начальной функцией) будем искать в классе равномерно

ограниченных функций», приводит начальную задачу Коши в класс

корректных (по Адамару), т.е. имеющих и притом единственное

решение, устойчивое по начальным данным. Но, как показывает пример

А. Н. Тихонова, если не накладывать ограничение на рост решения с

увеличением времени, то построенное решение уже не будет

единственным [146].

Приведенные принципы сравнения также переносятся и на

некоторые уравнения (например, на закон сохранения), которые

получаются путем предельного перехода (например, с помощью метода

исчезающей вязкости) из нелинейных параболических уравнений.

В доказательстве часто в качестве сравниваемых функций

выбираются: решение рассматриваемой задачи и специальным образом

подобранное автомодельное решение (асимптотически автомодельное

решение) либо специальным образом «склеенная» функция из таких

решений. При этом значения на

x  

(а также ординаты «склеек», в

случае если таковые имелись) у таких автомодельных решений

выбираются из множества точек

 

0 0 1 1

, , ,..., , ,

n n n

     



либо из малых окрестностей этих точек, а сдвиги фаз подбираются так,

чтобы в начальный момент времени выполнялись условия использу-

емого варианта принципа сравнения.

Заметим, что основные идеи описанного подхода к доказательст-

ву теорем 1, 2 применялись ранее для исследования асимптотики (по

времени) решения начальной задачи Коши для уравнения теплопровод-

136

ности с нелинейным источником (такого рода уравнения возникают, на-

пример, при описании распространения генных волн и пламени). Так,

еще в 1937 г. в пионерской работе А. Н. Колмогорова, И. Г. Петровско-

го, Н. С. Пискунова [137] была исследована сходимость к одной бегу-

щей волне. Современное состояние дел отражено в работах [136, 138] и

цитированной там литературе.

Следуя монографии [136], можно называть сходимость в теореме

2 сходимостью по форме. А согласно терминологии работы [133], сис-

темы волн, возникающие в теоремах 1, 2, следует называть промежу-

точными асимптотиками (заметим (см. теорему 2), что промежуточная

асимптотика (система волн), в общем случае сама не обязана являться

решением уравнения).

2.3.2. Эволюции локального затора в транспортном потоке, описы-

ваемом моделями LWR и Уизема

Предположим, что в однородном стационарном транспортном по-

токе (одна бесконечная полоса без въездов и выездов) образовалось ло-

кальное увеличение плотности (локальный затор). Проследим (не стро-

го!) за эволюцией этого «бугорка» (за тем, как будет рассасываться это

локальное увеличение плотности). Для этого введем

 

АТС/км –

«высоту» бугорка и

 

км – «длину» бугорка в момент времени

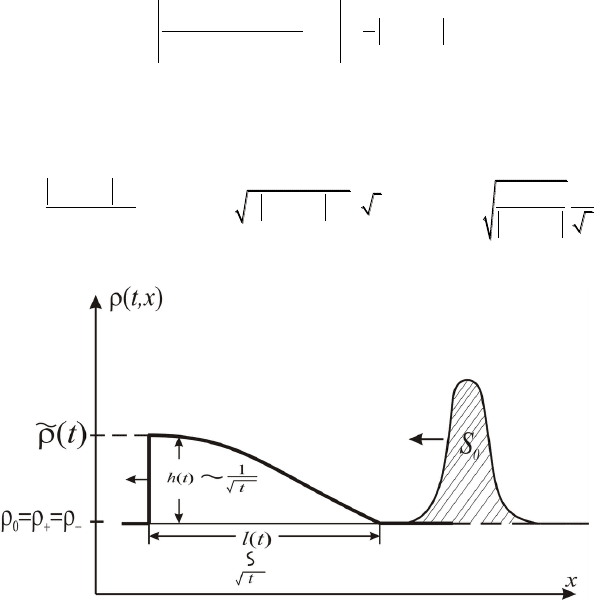
(см.

рис. 21). Поскольку площадь бугорка сохраняется (что как раз и отража-

ет закон сохранения количества АТС), то

   

2h t l t S

где

– площадь (размерность площади – АТС) под бугорком. Здесь

стоит приближенное равенство из-за того, что бугорок, вообще говоря,

не будет в точности иметь вид прямоугольного треугольника (гипотену-

за, в общем случае, будет кривой линией и лишь на больших временах

достаточно хорошо приближается прямой). Сам факт, превращения (с

ростом времени) произвольного бугорка в криволинейный прямоуголь-

ный треугольник (так же, как на рис. 7, считаем, что

 







) не-

сложно устанавливается с помощью метода характеристик.

Перейдем теперь в систему координат, движущуюся со скоро-

стью

 







137

где



– значение плотности вдали от бугорка. В этой системе коорди-

нат «скорость разбегания бугорка» можно посчитать по формуле RRH:

 

   

Q t Q

l t c Q h t









 

  





где

   

t h t







– максимальное значение плотности в момент времени

. Таким обра-

зом,

 











   

2l t Q S t









 







Сделанные качественные выводы неплохо согласуются с практикой.

Рис. 21. Эволюция локального затора

Приведенные выше рассуждения являются частным случаем бо-

лее общего и более точного утверждения «об асимптотике вида N-вол-

ны» (см. работы П. Лакса, Т.-П. Лю, Р. Ди Перна, К. Дафермоса, С. Н.

Кружкова и Н. С. Петросян [2, 7, 11, 35, 93, 96]).

Упражнение (см. [35, 42, 96]). Пусть, как и в приведенных выше

рассуждениях,

 





