Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation
Подождите немного. Документ загружается.

5.4 The Betz optimum blade dimensions
182
Having established this, the rotor should now be built in such a way that each ring
element 2
S
r dr of the swept rotor area extracts from the wind the power (Figs.
5-13 and 5-14)
drrvEd
S
U
2
227
16
3
1Betz
.
(5.31)
dr
r
ȍ
dr
r
ȍ
Fig. 5-14 Ring section of area dA = 2
S
r dr
This power will be extracted with z appropriately dimensioned blades. It results in
a mechanical power of
dP = z · dU · ȍ r . (5.32)
number tangential local circumferential
of blades component velocity
of the
aerodynamic force
at the ring section.
Since we assume that at the design point the aerodynamic profile is operated close
to its best lift/drag ratio, the drag coefficient is very small, c
D
<< c
L
. The lift is
then the only significant contributor to the tangential force dU in equation (5.29)
dU § dL sin
I
=
U
c
L
w
2
c (r) dr sin
I
. (5.33)
5 Blade geometry according to Betz and Schmitz
183
The mechanical power is now given by
dP § z r
U
c
L
w
2
c (r) dr sin
I
(5.34)
Equating the mechanical power (5.34) and the Betz power (5.31),
dP = Ed
Betz
, the important formula for the blade chord c(r) of an optimally de-
signed blade can be obtained:
c(r) =
I
S
sin
2
27
161
2
3
L
rw
v
c
r
z
:
. (5.35)
Using the relations given in the triangles of velocities,
v
1
=
2
3
w sin
I
and u = ȍ r = w cos
I
we can rewrite this as
c(r) = 2
S
R
9
4
1
9
81
22
DD
L
R
r
cz
OO
. (5.36)
In this equation,
O
D
is the chosen design tip speed ratio and c
L
the lift coefficient
selected in the course of the design process. It can – but does not have to – be con-
stant along the radius r. It is common practice to select a design value c
L
close to
the best lift/drag ratio, i.e.
c
L
= 0.6 to 1.2
Į
A
= 2° to 6°
}
H
= c
L
/ c
D
|
H
max .
In equation (5.36) which only distributes the required total blade chord over sev-
eral blades there is no information on how to choose the number of blades. The
blade number can be determined based on such issues as material strength, manu-
facturing or dynamic aspects.
The equation (5.36) for the blade chord becomes even more transparent in its
simplified approximation
5.4 The Betz optimum blade dimensions
184
c(r)
§ 2 ·
S
· R ·
¸
¹
·
¨
©
§
R
r
cz
2
D
L
1
9
81
O
, (5.37)
This simplification can be used for turbines with a high tip speed ratio (Ȝ
D
> 3) and
if we assume that the profiled begins at about 15% of the outer radius due to the
space required for the hub. From the formula, it becomes clear that the blade chord
required for the extraction of the Betz power actually decreases proportional to the
square of the tip speed ratio Ȝ
D
.
Tip speed ratio Ȝ
D
Wind turbine
1930-1950
Wind pump
1880-1940
Ratio of total blade area and swept area ĭ
F
Tip speed ratio Ȝ
D
Wind turbine
1930-1950
Wind pump
1880-1940
Ratio of total blade area and swept area ĭ
F
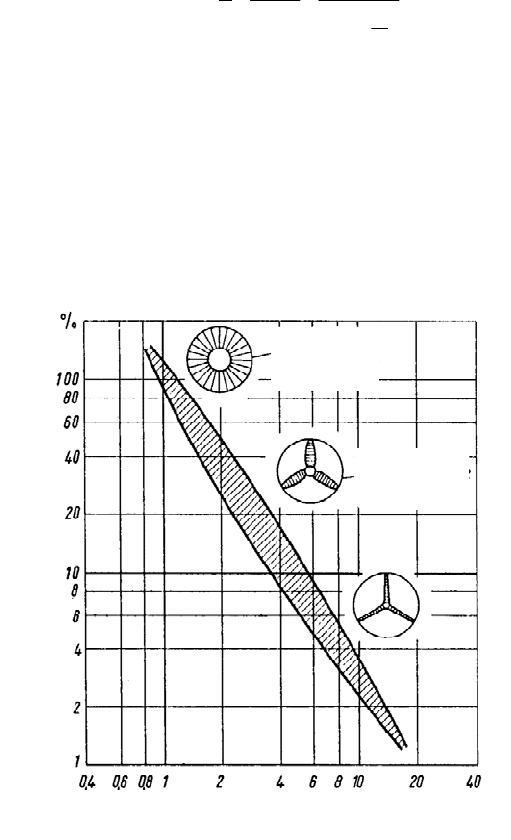
Fig. 5-15 Degree of solidity (ratio of total surface area of the blades to swept rotor area) versus
design tip speed ratio Ȝ
D
[12]
5 Blade geometry according to Betz and Schmitz
185
́
10
Ȝ
D
= 4
́
́
8
6
Ȝ
D
= 4
1
2
3
4
5
r in m
0
012
Blade chord c(r) in m
Relative wind direction ́(r)
R = 5 m
r
=
1
m
2
r
=
1
m
2
r
=
1
m
2
r
=
1
m
2
Ȝ
D
= 6
Ȝ
D
= 8
Ȝ
D
= 10
́
́
10
Ȝ
D
= 4
́
́
8
6
Ȝ
D
= 4
1
2
3
4
5
r in m
0
012
Blade chord c(r) in m
Relative wind direction ́(r)
R = 5 m
r
=
1
m
2
r
=
1
m
2
r
=
1
m
2
r
=
1
m
2
Ȝ
D
= 6
Ȝ
D
= 8
Ȝ
D
= 10
́
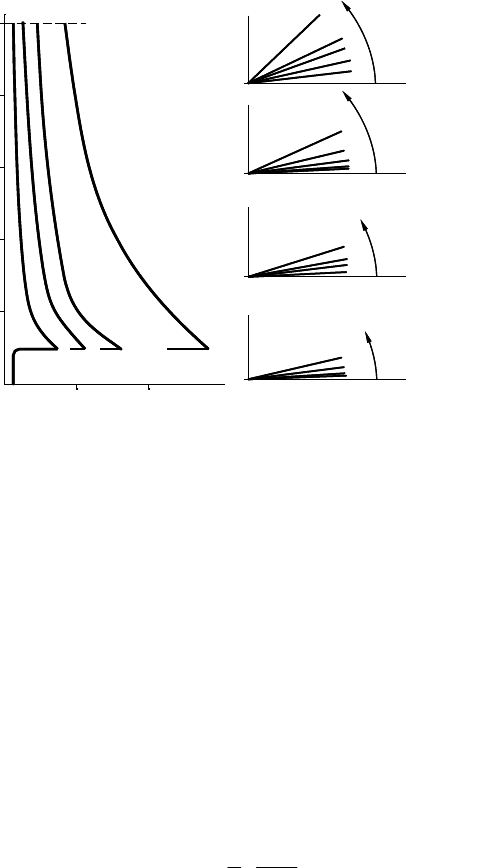
Fig. 5-16 Influence of design tip speed ratio Ȝ
D
on blade chord length c(r) and direction of the
relative velocity
I
(r) in the rotor plane; three-bladed rotor of Betz design, D = 10 m
Hütter developed the diagram, Fig. 5-15, which shows the degree of solidity ver-
sus the chosen design tip speed ratio. The scatter results from the base range of c
L
values close to 1.0.
In addition to the blade chord, the (total) blade twist angle
E
(r) of the profile
E
(r) =
I
(r) -
D
A
(r) (5.38)
must be determined, see Figs. 5-11 and 5-13. By selecting the tip speed ratio
O
D
,
we can determine the angle
I
of the relative velocity w in the rotor plane contin-
gent on the radius r, see equation (5.26) and Fig. 5-16
I
r = arctan
¸
¸
¹
·
¨
¨
©
§
D
3
2
O
r
R
.
The angle
I
of the relative velocity w is the first contribution to the blade twist.
The blade chord has to be inclined in relation to this angle
I
by the angle of attack
D
A
corresponding to the lift coefficient c
L
taken as a basis for the profile chord
length, Fig. 5-13. Therefore, the total blade twist angle is given by

5.5 Losses
186
E
= arctan
¸
¸
¹
·
¨
¨
©
§
D
3
2
O
r
R
-
D
A
(r) . (5.39)
This is the local angle between rotor plane and chord line.
5.5 Losses
The Betz power coefficient from equation (5.9) is attained only by an ideal
machine
c
P.Betz
=
27
16
= 0.59 .
It only takes into account the losses of the axial downstream velocity. Moreover,
there are further sources of losses, most importantly:
- the profile losses resulting from the drag force ignored in equation (5.34),
- the losses resulting from the flow around the blade tip from the pressure to the
suction side, the so-called tip losses, and
- the wake losses due to the wake rotation downstream.
5.5.1 Profile losses
The profile losses are caused by the drag of the profile. These can be ignored
when determining the ideal optimum blade geometry. However, they must be
taken into account when calculating the power balance. Equation (5.32) together
with equation (5.29) gives the real power at the blade element
dP = z ȍ r dU
= z ȍ r
»
¼
º
«
¬
ª
II
U
cossin
DL
2
ccdrcw
. (5.40)
which takes into account the drag. For an ideal wind turbine, on the other hand,
there is no drag (c
D
= 0)
dP
ideal
= z ȍ r
U
w
2
c dr c
L
sin
I
.

5 Blade geometry according to Betz and Schmitz
187
The ratio of dP/dP
ideal
gives the profile efficiency
K
Profile
= 1
L
D
c
c
I
tan
1
= 1
H
1
I
tan
1
(5.41)
= 1
H
O
D
2
3
R
r
,
if tan
I
is expressed by equation (5.26). The losses at the ring section under con-
sideration are proportional to the design tip speed ratio Ȝ
D
and the radius r
[
Profile
=
H
O
D
2
3
R
r
. (5.42)
these losses increase with the proximity to the tip, but they are inversely propor-
tional to the lift/drag ratio. Since the biggest portion of the power is extracted at
the outer sections of the blade, wind turbines designed with a high tip speed ratio
require high-quality profiles (İ
max
> 50) for this part of the blade. In the inner
rotor blade sections and for wind turbines designed with a low tip speed ratio
(Western mill
O
D
§ 1, Dutch smock mill
O
D
§ 2) the quality of the profile is not an
issue.
If a single airfoil profile type is used along the entire blade length with a fixed
angle of attack
D
A
, the lift/drag ratio
H
is independent of the local radius r. It is
then possible to integrate explicitly the power (and the profile losses) along the
radius
P =
U
27
16
³
R
drrv
S
K
Profile
3
1
,
P =
3
1
27
16
v
U
drr
R
r
R
S
H
O
¸
¹
·
¨
©
§
³
D
2
1 or (5.43)
5.5 Losses
188
P =
3
1
27
16
v
U
»
¼
º
«
¬
ª
H
S
O
D
2
1R .
In this case, the ratio of tip speed ratio and lift/drag ratio describes the total loss
resulting from the profile drag.
Here, the overall losses due to profile drag are simply described by the tip
speed ratio and the lift/drag ratio.
5.5.2 Tip losses
Another source of losses is the flow around the tip of the blade from the pressure
side (lower side of the profile) to the suction side (upper side). This causes the
blade lift to decreases toward the tip.
The superposition of the flow around the blade tip with the attacking wind creates
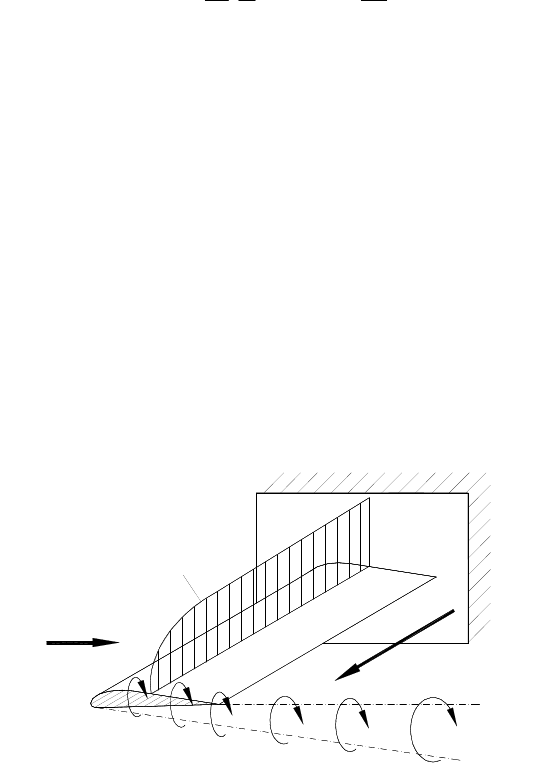
an expanding vortex washed downstream by the wind, Fig. 5-17.
The more slender the blade, the more it resembles an infinitely long blade (
R
/c
= ) for which the values of c
L
and c
D
from the profile catalogues hold true.
c
A
c(r)
r
c
L
w
c
A
c(r)
r
c
L
w
Fig. 5-17 Air flow around the blade tip from positive pressure side to suction side (tip vortex),
lift distribution c
L
(r)
In order to account for these losses at a blade of infinite length, Betz [1] introduces
an effective diameter D' instead of the actual diameter D. Based on the Prandtl
approximate method, this can be determined as follows
D' = D 0.44 b , (5.44)

5 Blade geometry according to Betz and Schmitz
189
where b is the projection of the distance a between the tips of neighbouring blades
(Fig. 5-18) onto a plane perpendicular to the direction of relative velocity w,
a =
z
D
S
, b =
I
S
sin
z
D
. (5.45)
If one introduces the relationships given in the triangle of velocities at the blade
tip
w sin
I
= v
2
; w
2
= (ȍ R)
2
+
2
2
v ,
and taking v
2
= 2 v
1
/3 for the design point, the reduced diameter D' is given by
¸
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
¨
©
§
9
4
3
2
44.1'
2
D
O
S
z
DD
. (5.46)
Since the power is proportional to the diameter squared, the efficiency that takes
into account the flow around the blade tip can be obtained from
¸
¸
¹
·
¨
¨
©
§
c
c
9
4
z
0.92
1
2
D
2
2
Tip
Ȝ
D
D
P
P
Ș
.
(5.47)
For a design tip speed ratio
O
D
> 2 , this can be simplified to
K
tip
§ 1
D
84.1
O
z
. (5.48)
Roughly speaking, this loss is in inverse proportion to the product of blade number
z and design tip speed ratio
O
D
:
[
tip
§
D
84.1
O
z
.
Table 5.1 shows these losses and the ratio of effective to actual diameter, D’/D for
some wind turbine types.
5.5 Losses
190
Table 5.1 Tip losses
[
tip
depending on the design tip speed ratio
O
D
and the number of blades z.
D' is the effective diameter
Wind turbine type
OO
D
z
OO
D
z
[[
tip
in %
D'/D
Western mill 1 20 20 9 0.95
Dutch smock mill 2 4 8 22 0.88
Danish concept
wind turbine
6 3 18 10 0.94
Single blade turbine
(Monopteros)
12 1 12 15 0.92
b
a
́
́
v
b
a
a
w
b
a
́
́
v
b
a
a
w
Fig. 5-18 Air distribution over the individual blades, Betz [1]
5 Blade geometry according to Betz and Schmitz
191
5.5.3 Losses due to wake rotation
These losses result from the extraction of torque at the active plane of rotation.
The principle of action equals reaction means that the tangential force dU creates a
counteracting torque on the downstream air flow via the lever r (Fig. 5-14). The
smaller the design tip speed ratio of the wind turbine, the higher is this torque.
This can be illustrated by equation (5.32) which gives the mechanical power dP in
the ring section dr,
dP = z · dU · ȍ r .
number circumferential circumferential
of blades force velocity
The wind turbine with a high design tip speed ratio extracts the power by a high
angular speed ȍ and a comparatively small torque r dU. The wind turbine with a
low design tip speed ratio does it the other way round: its rotational speed is low
and the aerodynamic torque r dU high – consequently the wake rotation of the air
flow downstream of the rotor is high.
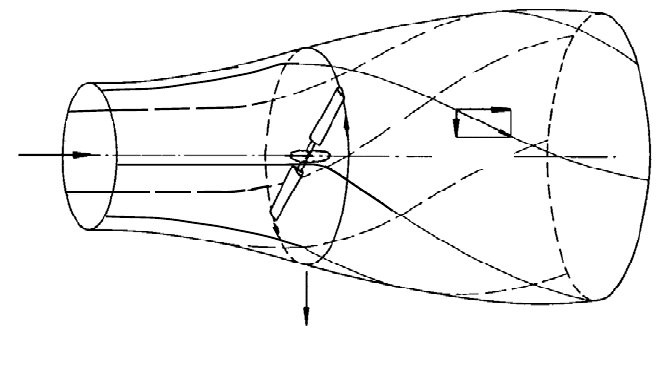
V
circumf.
v
axial
P
mech
< P
mech,Betz
v
1
=v
W
V
circumf.
v
axial
P
mech
< P
mech,Betz
v
1
=v
W
Fig. 5-19 Downstream wake rotation [10, modified]
Therefore, in contrast to Betz cf. equations (5.4) and (5.5), downstream losses are
now not only due to the axial velocity v
3
far downstream but there is also a
circumferential component v
circumf.
in the downstream flow causing additional
losses, the wake rotation losses, Fig. 5-19.
For turbines with a high tip speed ratio, Ȝ
D
> 3, these losses are very low. But
turbines with a low tip speed ratio, such as the Western mill with Ȝ
D
§ 1, cannot
reach the Betz power coefficient of c
P,Betz
= 0.59. Due to unavoidable swirl losses,
they can only reach a maximum coefficient of c
P,max
= 0.42. And this value should
