Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation

Подождите немного. Документ загружается.

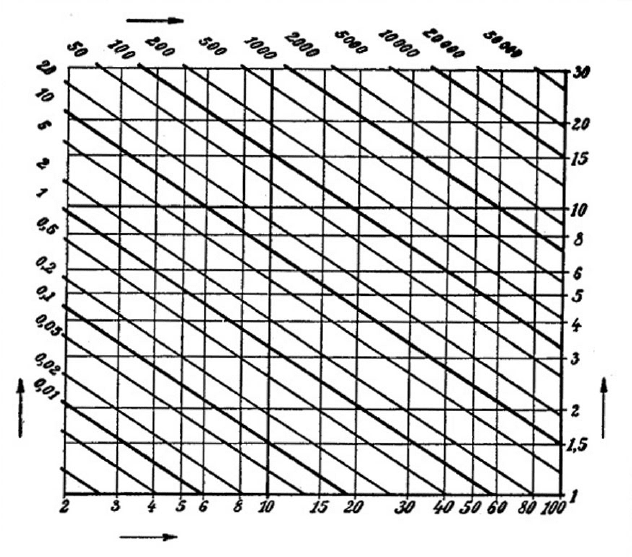
5.1 How much power can be extracted from the wind?

172

Wind speed in m/s

Diameter of wind wheel in m

Power in kW

Wind speed in m/s

Diameter of wind wheel in m

Power in kW

Fig. 5-4 “Betz power” of wind turbines as a function of wind velocity and diameter, Betz [1]

Remark: In the English literature, the power coefficient and the thrust are often

shown versus the “induction factor a”. This is based on the idea that the wind tur-

bine superimposes a sort of headwind av

on the wind velocity v

. For the active

rotor plane this gives

= v

(1- a)

and far downstream of the rotor

= v

(1- 2 · a).

We show this induction factor on an additional scale in Fig. 5-3.

5 Blade geometry according to Betz and Schmitz

173

5.1.1 Froude-Rankine Theorem

In the following it will be proved that the velocity v

in the rotor plane

according

to Betz’ theory is actually the arithmetic mean of the far-upstream and far-

downstream velocities.

The thrust can be expressed using the principle of linear momentum in equation

(5-10)





vvmT





Alternatively, it can be derived from the Bernoulli equation (energy balance),

which we apply for both the plane left and the plane right of the rotor plane, Fig.

5-5.



v =



 vp

and (5.13)



 vp

= p

v



. (5.14)

The subscript -2 denotes the plane immediately before the rotor, and +2 immedi-

ately after the rotor.

To preserve continuity, the velocity immediately left and right of the rotor must

be equal, v

-2

= v

. Moreover, the static pressure far upstream and far down-

stream are also equal, p

= p

. Hence, the difference of equation (5.13) and (5.14)

gives





vv 

= p

-2

 p

(5.15)

According to these (energetic) considerations, the thrust at the tower results from

the difference of the static pressure before and after the rotor plane

T = A · (p

-2

 p

) . (5.16)

5.1 How much power can be extracted from the wind?

174

(x)

-2

(x)

Fig. 5-5 Development of velocity and static pressure p along the stream tube

Putting the mass flow rate



= ȡ A v

into equation (5.10) and introducing this

into the equations (5.16) and (5.15), we obtain the expression used in section 5.1

for the velocity v

in the rotor plane

)(

vv 

5 Blade geometry according to Betz and Schmitz

175

5.2 The airfoil theory

So far, the method of power extraction at the rotor plane has been left open. Hori-

zontal axis wind turbines use rotating blades designed to extract the maximum

power as calculated by Betz. Before we start the discussion of blade dimensioning,

the basic results of the airfoil theory will be presented.

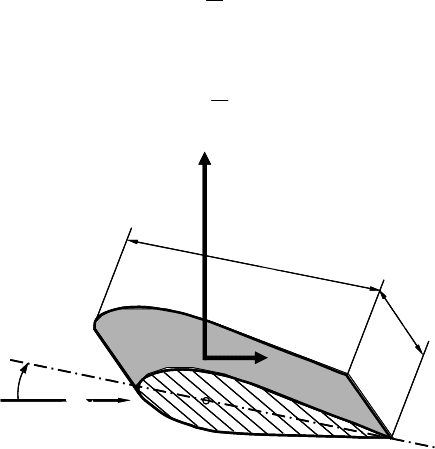
For that purpose, we consider a symmetric airfoil profile attacked at the leading

edge by a velocity w. When the angle of attack is

$

= 0° no lift occurs, only

drag. For a streamlined airfoil, as shown in Fig. 5-6, it is small.

The positive lift force L results from an angle of attack greater than zero. It is

proportional to the blade area (chord length c times width b), and to the square of

the velocity w.

L = c

(

)



(c b) (5.17)

D = c

(

)



(c b) (5.18)

Fig. 5-6 Lift F

and drag F

at a blade element of the width b and chord length c

The lift coefficient c

= c

(Į

) denotes the dependence on the angle of attack Į

Like the drag coefficient c

(Į

), it is usually determined by means of wind tunnel

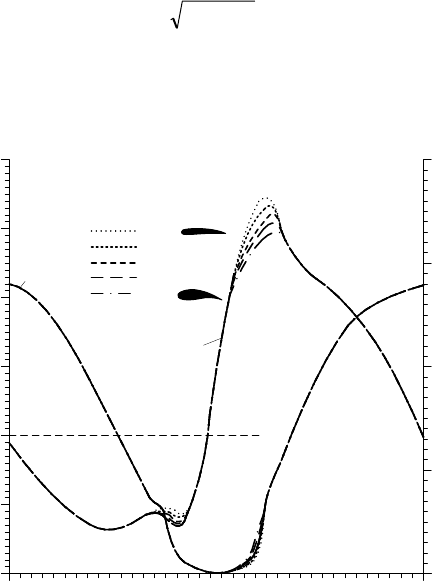
experiments. Fig. 5-7 shows the measured curves of lift and drag coefficients for

an asymmetric profile.

Initially, the increase in the lift coefficient c

(and thus the lift force) increases

linearly with the angle of attack (range 0° < Į

< 10°). Then, the curve flattens be-

fore reaching its maximum value. At even greater angles of attack, the flow sepa-

rates from the profile: the lift is reduced in this range (Į

> 15°), while c

, and

5.2 The airfoil theory

176

thus the drag force, increases rapidly with Į

, Fig. 5-7. This figure also shows that

the thinner the airfoil profile is the smaller its drag coefficient for small angles of

attack

The flow on the airfoil’s upper side (i.e. suction side) is faster than on the lower

side (i.e. pressure side) since it has to cover a larger distance. According to the

Bernoulli equation, this results in a lower pressure on the upper side. The integra-

tion of (p ds) along the profile contour gives the lift L and the drag D as compo-

nents of the resulting force F, Fig. 5-9,

F =

DL  . (5.19)

Angle of attack Į

-90 -45 0 45 90

2.0

1.5

1.0

0.5

0.0

-0.5

-1.0

2.0

1.5

1.0

0.5

0.0

Fig. 5-7 Corrected lift and drag coefficients versus angle of attack Į

from wind tunnel

measurements for the profiles NACA 4412 to 4424 [9]

5 Blade geometry according to Betz and Schmitz

177

= 3°

= 19°

= 3°

= 19°

Fig. 5-8 Pressure distribution around an airfoil [13], a) for a small angle of attack (Į

= 3°);

b) for a large angle of attack (Į

= 19°)

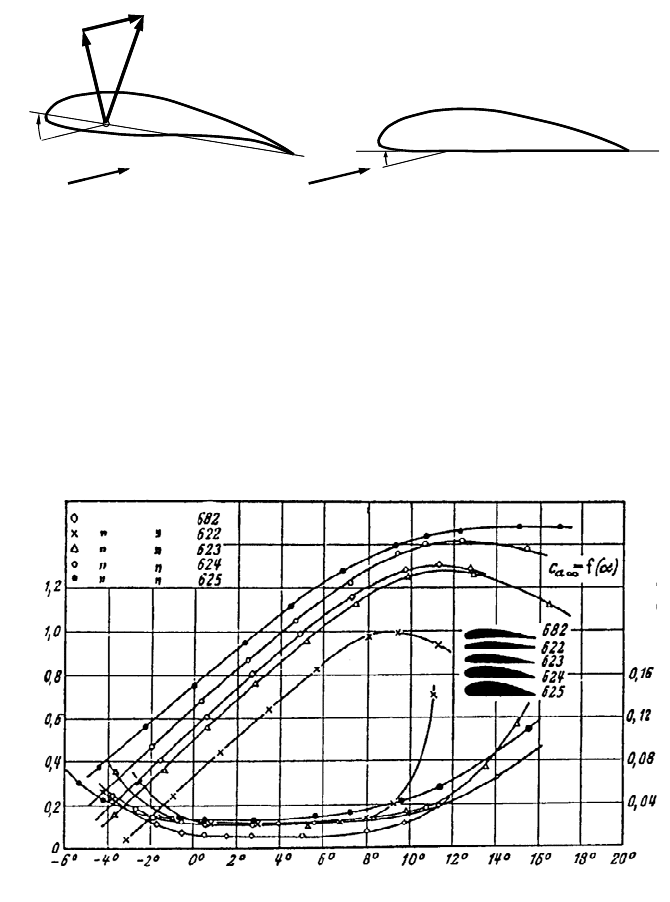
As long as the flow is attached, this force F attacks at a point between 25 and 30%

of the profile’s chord length c. If the flow is separated, this point moves further

back; during heavy stall conditions it is found around c/2 which is immediately

plausible for

= 90°. For this case, the blade’s surface is perpendicular to the at-

tacking flow w, and the pattern of the flow around the blade is nearly symmetrical.

For the case of a flat plate with attached flow, the lift coefficient can be deter-

mined theoretically [6]

(

) = 2

A .

(5.20)

For real airfoil profiles the lift coefficient c

is slightly smaller

(

) = (5.1 to5.8) D

. (5.21)

In catalogued measurements of asymmetric profiles [e.g. 3, 4, 5], it is important to

check whether the angle of attack is measured from the resting edge (which will

often be the case for profiles with a straight lower side), or from the chord line be-

tween nose centre of the leading edge and trailing edge, Fig. 5-9. In any case, the

point of zero lift, c

= 0, is found in the range of negative angles of attack. At

= 0° there is a lift due to the camber of the profile, see Fig. 5-10.

As for the symmetric profiles, the gradient c

´ in the rising part of the lift curve

for the asymmetric profile is approximately c

´ # 2 S.

In the next section the lift/drag ratio will be used which gives the ratio between

lift force and drag force

H

(

) =







ǹL

. (5.22)

5.2 The airfoil theory

178

Res

Fig. 5-9 Reference line for the definition of the angle of attack: Force F

Res

resulting from lift

force L and drag force D

Its maximum

max

(usually found in the range c

= (0.8 to 1.1), at moderate an-

gles of attack) is a measure for the aerodynamic quality of the profile. High-

quality profiles attain a lift/drag ratio of

max

= 60 and higher; a flat plate may

achieve a value of

max

= 10. Be careful: there are different definitions to be

found in the literature. Sometimes the inverse lift/drag ratio is applied, see Fig. 5-

10.

Angle of attack Į

Göttingen profile

Lift coefficient c

Drag/ lift ratio

Angle of attack Į

Göttingen profile

Lift coefficient c

Drag/ lift ratio

Fig. 5-10 Lift coefficients c

and inverse lift/drag ratio of some Göttingen airfoil profiles [11]

5 Blade geometry according to Betz and Schmitz

179

5.3 Flow conditions and aerodynamic forces at the rotating

blade

5.3.1 Triangles of velocities

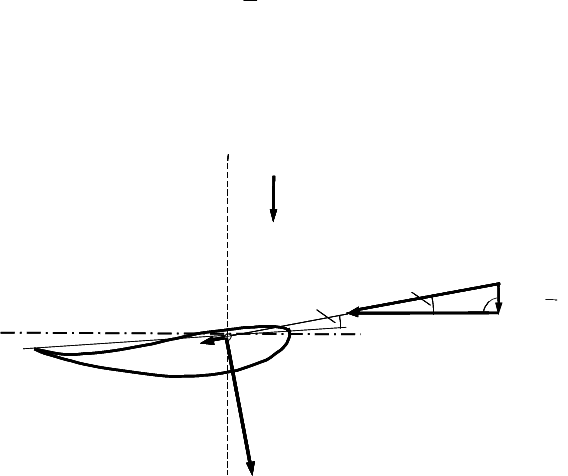
There is a relative velocity w for each cross section r of the blade. This velocity

consists of the retarded velocity in the rotor plane v

= 2 v

/3 according to Betz,

and the local circumferential speed u =

r resulting from the blade’s rotation

with the angular speed .

In Fig. 5-11 we see immediately that the relative velocity w is composed of the

two components v

and u(r)

(r) =

v +





r: . (5.23)

Its direction

I

in reference to the rotor plane is given by

tan

I

(r) = v

/(:r) (5.24)

Wind

Machine axis

Wind

Rotor plane

Wind

Machine axis

Wind

Rotor plane

Fig. 5-11 Triangles of velocities, relative velocity w resulting from the geometrical superposi-

tion of the reduced wind velocity v

in axial direction, and the circumferential speed u = ȍr,

resulting from the blade’s rotational speed

Introducing the design tip speed ratio

which is the quotient of circumferential

speed ȍ R at the blade tip and the wind velocity v

5.3 Flow conditions and aerodynamic forces at the rotating blade

180

O

(5.25)

we can modify equation (5.24) with v

= 2 v

/3 to

tan

. (5.26)

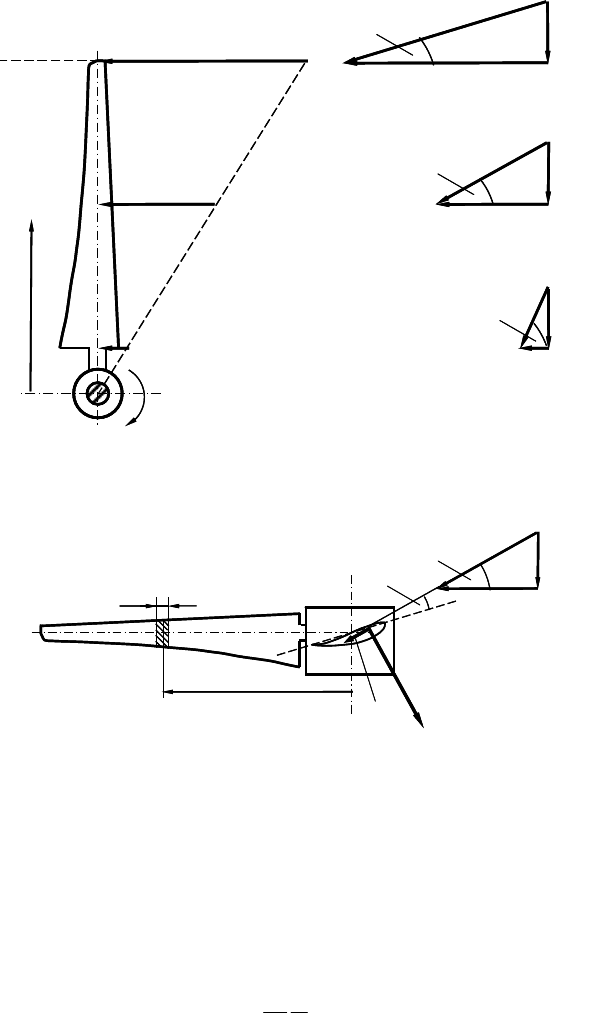
Fig. 5-12 illustrates once more that the triangles of velocity vary for each blade

section, as the circumferential component u = ȍ r increases linearly with the

radius.

5.3.2 Aerodynamic forces at the rotating blade

According to Fig. 5-13, the aerodynamic forces lift dL and drag dD pull and push

(approx. at 0.25 of chord) at the blade element of length dr at the radius r,

Lift: dL =



c dr c

(

) and (5.27)

Drag: dD =



c dr c

(

) . (5.28)

The lift force is perpendicular to the direction of the relative velocity w whereas

the drag is parallel to it, cf. section 5.2. Therefore, the decomposition of these

forces into the tangential force dU in the circumferential direction and the thrust

dT in the axial direction yields (Fig. 5-13)

dU =



c dr [c

sin

 c

cos

I

] and (5.29)

dT =



c dr [c

cos

 c

sin

] . (5.30)

5 Blade geometry according to Betz and Schmitz

181

Fig. 5-12 Triangles of velocity at different blade sections: circumferential speed u = ȍr, axial

wind velocity at the plane of rotation v

= 2 v

u(r)

w(r)

Drag

Lift

u(r)

w(r)

Drag

Lift

Fig. 5-13 Aerodynamic forces at the blade ring element dr

5.4 The Betz optimum blade dimensions

According to the general considerations in section 5.1, the maximum power that

can be extracted from a circular area is





Betz

227

RvE

