Gasch R., Twele J. (Eds.) Wind Power Plants: Fundamentals, Design, Construction and Operation

Подождите немного. Документ загружается.

4.2 Atmospheric boundary layer

132

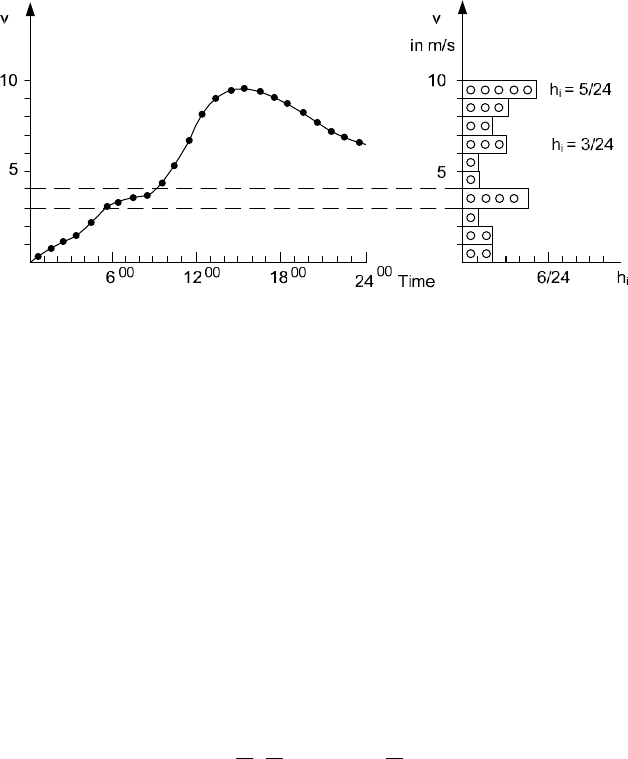
Frequency distribution – Histogram of wind speeds

For the wind turbine design as well as for the assessment of the expected energy

yield, the pure time series of possibly several years of measurement are quite

impractical. One possibility for attaining a compressed representation of the wind

conditions is the generation of a frequency distribution of the wind speed. The

wind speeds are sorted into classes and summed up, Fig. 4-18. This way, the tem-

poral share of the individual wind speed class of the entire considered time period

is determined. The width of the wind speed class is typically 1 m/s.

Fig. 4-18 Left: Diurnal time series of hourly averaged values; right: corresponding histogram of

the relative frequency h

of the respective day

The relative frequency of the individual wind speed class v

is h

= t

/T, e.g. hours

per 24 hours in Fig. 4-18. Of course, the sum of the relative frequencies must be

exactly 1.0, resp. 100%. Fig. 4-21b shows such a frequency distribution of the

Tauern wind farm (Austria) with a wind speed class width of 1 m/s. In section 4.3

it will be presented how to calculate the expected energy yield with such a wind

speed histogram and a given wind turbine power curve, cf. Fig. 4-25.

Wind speed distribution function

The measured frequency distribution is mostly “compressed” into a mathematical

description using the Weibull distribution function which is quite flexible due to

its two parameters



 k1k

exp)(

. (4.11)

4 The wind

133

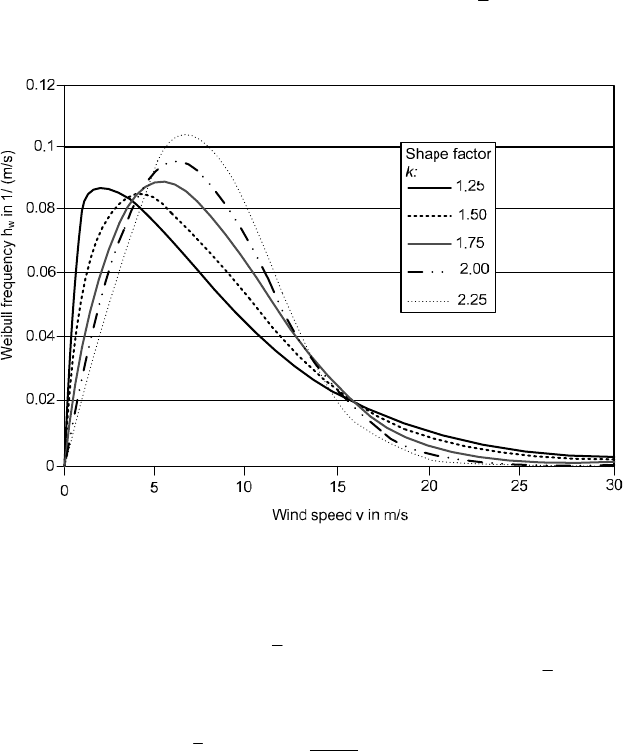
The scaling factor A is a measure for the characteristic wind speed of the consid-

ered time series. The shape factor k describes the curve shape. It is in the range

between 1 and 4, and the value is roughly characteristic for certain wind climate:

k § 1: Arctic regions

k § 2: Regions in Central Europe

k § 3 to 4: Trade wind regions

If there are small fluctuations around the mean wind speed v the value of k is

high whereas large fluctuations give a smaller shape factor k, Fig. 4-19.

Fig. 4-19 Example of Weibull distributions for a mean wind speed v = 8 m/s and different shape

factors k

Table 4.2 shows for some sites in Germany the Weibull factors A and k as well as

the corresponding mean wind speed v .

Given Weibull factors allow an estimation of the mean wind speed

[33]

k/1

434,0

568,0

|

. (4.12)

Both Weibull factors A and k change with the height above ground, Fig. 4-20.

4.2 Atmospheric boundary layer

134

Table 4.2 Weibull factors for different sites in Germany, measuring height 10 m, from [36]

Site k A in m/s

v in m/s

Helgoland 2,13 8,0 7,1

Hamburg 1,87 4,6 4,1

Hannover 1,78 4,1 3,7

Wasserkuppe 1,98 6,8 6,0

Fig. 4-20 Change of Weibull factors with height [1]

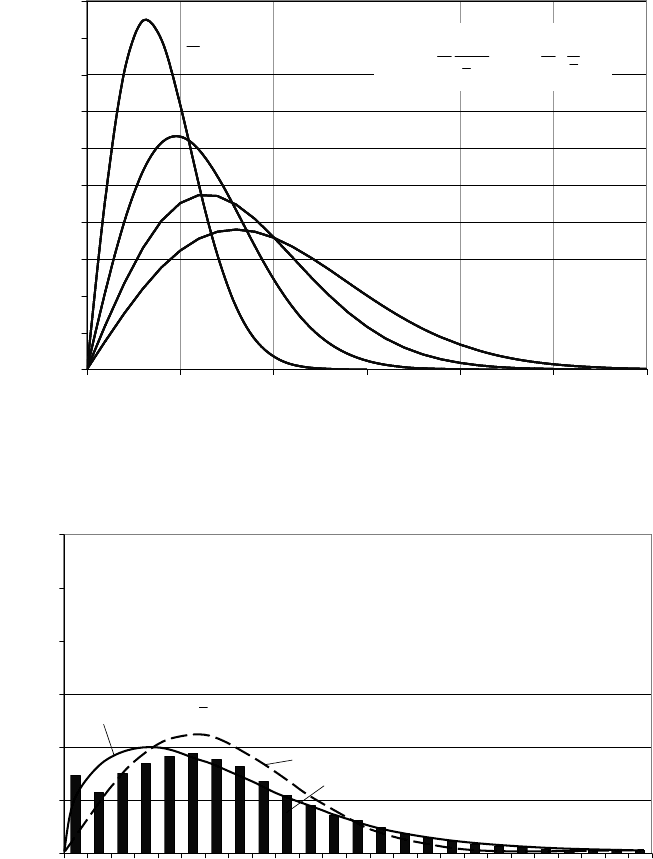
The Rayleigh distribution function, Fig. 4-21 (a), is a special, simplified case of

the Weibull distribution function for the shape factor k = 2.





exp

)(

. (4.13)

It is very straightforward since it depends only one parameter: the mean wind

speed v , e.g. the annual mean wind speed which is roughly known for many sites.

In general, the reference energy yield given by wind turbine manufacturers in the

data sheets is calculated based on a Rayleigh distribution function.

4 The wind

135

Fig. 4-21 (b) shows for the site of the Tauern wind farm a measured wind speed

frequency distribution and the fitted curves for both, the Weibull and the Rayleigh

distribution function. The differences between the measurement results and the

analytic description are strong.

If the analytic approximations by the distribution functions are used for the

yield calculation the following criteria should be considered:

- The calculated wind energy of the analytic and measured frequency distri-

bution should be approximately equal.

- For wind speed classes higher than the measured mean wind speed the

frequencies should be identical.

- The sum of the frequencies should be used as checksum and always be

1.00, else the relative frequencies have to be weighted with the used wind

speed class width (e.g. 0.5 m/s).

Moreover, the analytic description should represent correctly the classes which

contain the maximum energy. The determination of the Weibull factors for a given

measured frequency distribution is done e.g. by least square fitting, eventually it is

beforehand necessary to take twice the logarithm [7, 34].

Note: If the measured frequency distribution, Fig.s 4-18 and 4-21, (discrete rep-

resentation) is transformed into a distribution function h(v) (continuous represen-

tation) or vice versa, it has to be considered that h

= h(v) dv § h(v

) 'v

, since the

distribution function has the dimension 1/(m/s). A different wind speed class

width

causes other relative frequency values h

, which is obvious: the larger

the class width of the distribution function the more events are found within this

class, h

= t

/T.

The Weibull distribution function with its two factors is quite useful to describe

the histograms. But even if measuring the wind at a site for several years, extreme

events like the 50-year wind speed are perhaps not recorded because they did not

occur. So they have to be represented separately, cf. chapter 9.

Moreover, the analytic distribution functions are not very suitable to represent the

range of calms, since the functions always start with the value h (v = 0 m/s) = 0.

Frequencies of less than 1%, i.e. 10-min average values with less than 525 events

per year, may not be estimated with a Weibull distribution. Therefore, if the calms

statistics are required, e.g. for wind pumping and stand-alone systems, they are

recorded separately.

4.2 Atmospheric boundary layer

136

0,00

0,02

0,04

0,06

0,08

0,10

0,12

0,14

0,16

0,18

0,20

0 5 10 15 20 25 30

Windgeschwindigkeit v in m/s

Relative Häufigkeit h

(v ) in 1/(m/s)

v = 4 m/s





exp

)(

0,00

0,02

0,04

0,06

0,08

0,10

0,12

0,14

0,16

0,18

0,20

0 5 10 15 20 25 30

Windgeschwindigkeit v in m/s

Relative Häufigkeit h

(v ) in 1/(m/s)

v = 4 m/s





exp

)(

Wind speed v in m/s

Relative frequency h

(v) in 1/ (m/s)

0,00

0,02

0,04

0,06

0,08

0,10

0,12

0,14

0,16

0,18

0,20

0 5 10 15 20 25 30

Windgeschwindigkeit v in m/s

Relative Häufigkeit h

(v ) in 1/(m/s)

v = 4 m/s





exp

)(

0,00

0,02

0,04

0,06

0,08

0,10

0,12

0,14

0,16

0,18

0,20

0 5 10 15 20 25 30

Windgeschwindigkeit v in m/s

Relative Häufigkeit h

(v ) in 1/(m/s)

v = 4 m/s





exp

)(

Wind speed v in m/s

Relative frequency h

(v) in 1/ (m/s)

Wind speed v in m/s

Relative frequency h

(v) in 1/ (m/s)

12345678910111213141516171819202122232425

Wind speed class in m/s

Relative frequency in %

Measuring height: 10 m

Measuring period: 03/97 to 09/02

Height above sea level: 1835 m

Temperature: 8 °C

Measurements: 2038 days (2935090 1 min-values )

Rayleigh curve for

= 6,76 m/s

Weibull curve for

= 7,44 m/s and

= 1,46

Measurement

Fig. 4-21 a) Frequency distribution according to Rayleigh for different mean wind speeds;

b) measurements in the “Tauernwindpark” in Austria, wind speed histogram and the fitted

Weibull and Rayleigh frequency distribution functions [www.tauernwindpark.com]

4 The wind

137

10.0

12.5

0-5 m/s

5-10 m/s

10 - 15 m/s

15 - 20 m/s

20 - 40 m/s

7.5

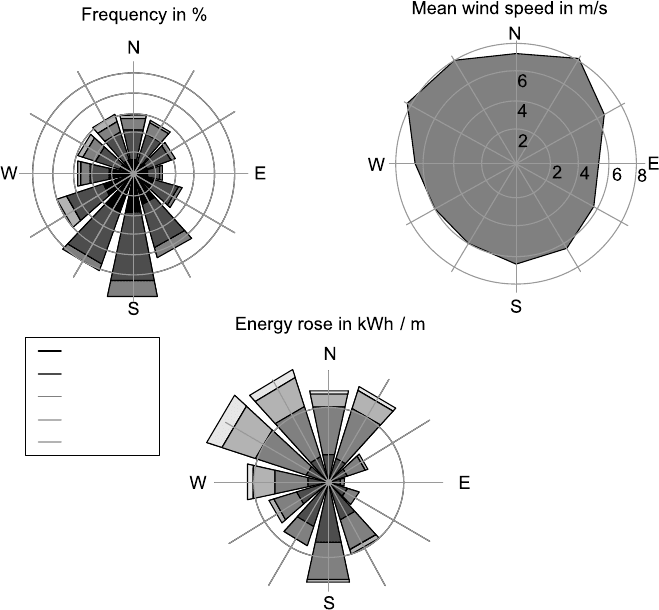
Fig. 4-22 Wind roses: Frequency rose, rose of mean wind speed and energy rose

For siting wind farms with more than one wind turbine it is important to know the

frequency distributions of the wind speed for the different wind directions in order

to arrange the wind turbines sophistically to prevent that the turbines shade each

other, cf. section 4.3.5. This sectorised wind information is represented in a wind

rose, Fig. 4-22. Three types of roses are important: the wind speed rose, the fre-

quency rose and the energy rose.

The wind speed rose shows the mean wind speed in the individual wind direc-

tion sectors. In Fig. 4-22 the highest mean wind speeds are observed in the sectors

NNE and WNW, while the Eastern wind is the smallest. In contrast, the wind fre-

quency rose, shows a clear dominance of the Southern wind directions. But since

the energy is proportional to the cube of the wind speed, and the Southern wind di-

rections show relatively small mean wind speeds, the North-western sectors in the

energy rose provide the largest energy share. These considerations serve for find-

ing an optimum wind farm layout where, among others it is important to prevent

that the turbines shade each other which reduces the energy yield and increases the

loads due to wake effects, Fig.s 4-28, 4-29 and 4-39.

4.2 Atmospheric boundary layer

138

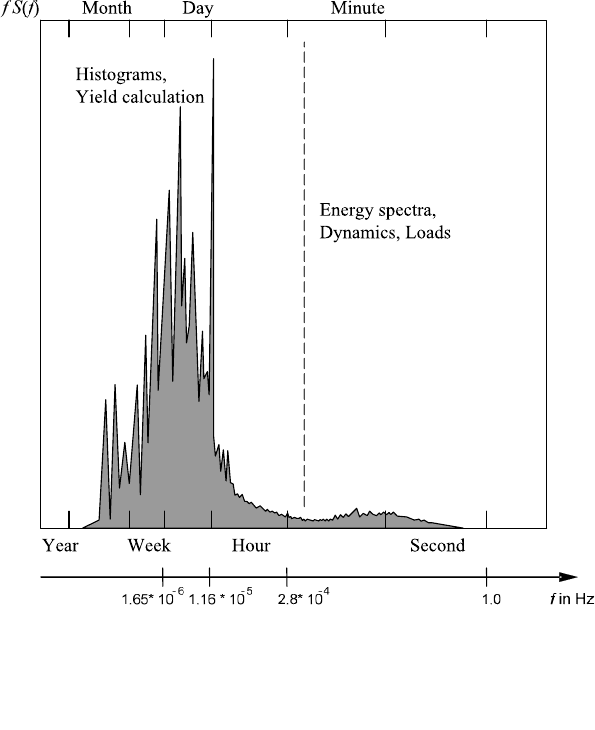
4.2.5 Spectral representation of the wind

The description of the wind by histograms and distribution functions is suitable for

the yield calculation, but the information on the time history is lost.

Vibrations and the dynamic loading on blades, drive train and tower occur in

the frequency range of 0.1 to approx. 30.0 Hz. The structure is very sensitive at

frequencies close to the individual natural frequencies of the components and re-

acts very “nervous”. The spectral representation of the wind is very suitable to in-

vestigate this frequency range which is found to the right in Fig. 4-23. The Fast

Fourier Transform is used to transfer the time domain data (the measured time se-

ries) into the frequency domain to obtain the power spectral density S. It has the

dimension (m/s)

/Hz = W/kg and describes the share of the individual frequency f

(in Hz) to the variance

v , equation (4.8) (resp. to the standard deviation

)

)( dffSv , (4.14)

The spectral representation is also very suitable for the generation of “synthetic

winds” for the digital simulation, cf. section 4.3.

Two spectral models of the wind are commonly used. The Kaimal spectrum

model was determined empirically from wind measurements

Kaimal spectrum model:

)/61(

)(

vLf



. (4.15)

The given turbulence length scale parameters L

and L

(Fig. 4-13) vary slightly

depending on the chosen guide lines.

The Kármán spectrum model is the second model and describes very well the tur-

bulence in wind tunnels and pipes, but is also often applied to describe the wind. It

allows quite easy to formulate the correlation between neighbouring points (e.g.

hub centre – middle of blade).

von-Kármán spectrum model:

6/52

))/(8,701(

)(

vLf



(4.16)

In general the power spectral density, Fig.s 4-23 and 4-24, is displayed versus the

frequency, but in Fig. 4-23 the time scale is added to relate the spectrum to Fig. 4-13.

4 The wind

139

Fig. 4-23 Power spectrum of wind speed based on a continuous measurement in flat and homo-

geneous terrain [11]

The power spectrum in Fig. 4-23 is based on a one-year measurement with a sam-

pling rate of 8 Hz. The fluctuations in the range of seconds and minutes, to the

right in the spectrum, are caused by atmospheric turbulence. The diurnal cycle of

the wind at the site creates the peak at the frequency (1/86400 s = 1.16*10

-5

Hz)

corresponding to the period of one day. The maxima in the spectrum in the range

of several days reflect large-scale weather events, e.g. the passage of an Atlantic

low-pressure system.

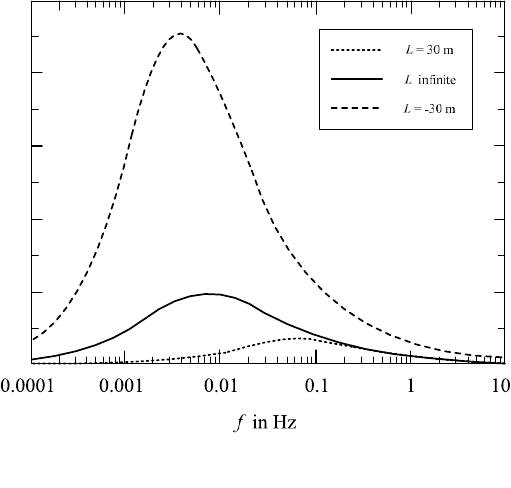
Fig. 4-24 shows schematically, for the case of flat, even terrain, the spectra for

the three different states of atmospheric stability, cf. section 4.2.1. The area below

the curve is proportional to the variance. Under neutrally stable conditions

(L = infinite) the spectrum is dominated by a broad maximum. At higher frequen-

cies f, it declines with the exponent f

–5/3

. Low frequencies are characterized by a

high variation and a high uncertainty. As explained in section 4.2.2 the tempera-

ture profile has a large influence on the vertical mass transfer and therefore on the

turbulence, cf. Fig. 4-10. The Fig. 4-24 shows a strong increase of the turbulence

4.2 Atmospheric boundary layer

140

in an unstable atmosphere (Monin-Obukhov stability length L = -30 m), whereas

stable stratification suppresses turbulence.

Up to now, only the longitudinal turbulence was considered since it dominates

in flat terrain. But in reality, turbulence is a three-dimensional phenomenon and in

flat terrain the ratio of the kinetic energies is approx. 1.0 : 0.8 : 0.5 for the longitu-

dinal, lateral and vertical direction. In complex terrain the proportions change, and

the lateral component becomes as strong as the longitudinal component (1.0 : 1.0 :

0.8), [19].



ffS

Fig. 4-24 Model spectra of the longitudinal wind speed component 50 m above ground in flat

terrain for neutrally stable (L = infinite), stable (L = 30 m) and unstable (L = - 30 m) conditions;

L stands for the Monin-Obukhov stability length [1]

Cross spectra and coherence functions

The turbulence spectra discussed above describe the temporal wind speed fluctua-

tions of the turbulent components at a single point in the rotor swept area of the

wind turbine. But since the turbine blades are moving through the turbulent wind

field it is not enough to consider the spectra at one single point. The spatial change

in lateral and vertical direction is also of importance because the blade is “collect-

ing” all the spatial changes, cf. section 8.1.

4 The wind

141

In order to reflect these effects, the spectral models of the turbulence have to be

expanded by the cross correlation of the turbulent fluctuations at two points of dif-

ferent lateral and vertical positions. The correlation is obviously decreasing with

increasing radial difference

r between the two points. Moreover, the correlation

is for the high-frequency changes smaller than for low-frequency changes. The

coherence Coh(

r, f) is measure for the relation between the turbulent fluctuations

at the two individual points “1“ and “2“ in the rotor plane. The coherence is

described depending on the frequency spectrum and the distance. It is defined as

follows

)()(

)(

),(

2211

fSfS

frCoh '

(4.17)

where S

(f) is the cross spectrum of the two points with the distance 'r,

and S

(f) und S

(f) are the auto spectra of the individual points. More details

on the spectral and coherence analysis is found in the literature [35, 37].

4.3 Determination of power, yield and loads

A prediction of the energy yield is possible using the measured wind speed and the

derived histograms, resp. distribution functions, and the given power curve of a

wind turbine. But since the wind is fluctuating strongly from year to year (cf. Fig.

4-17), it has to be verified whether the measuring period is representative enough

for a long-term prediction. This is done by a comparing and correlating evaluation

of wind data from neighbouring meteorological stations (also e.g. from airports)

where long-term measurements are documented.

For the prediction of the energy yield of a wind farm it is moreover necessary

to consider shading and disturbing effects at the site itself, and also from the

neighbouring wind turbines. During the years of operation, the real yield will be

surely smaller than the yield calculated in the first planning stages, because of

standstill time due to failure, maintenance and repair, see chapter 15.

4.3.1 Yield calculation using wind speed histogram and turbine

power curve

As discussed above, for a wind speed histogram with a given wind speed class

width, the relative frequency h

= t

/T of the individual wind speed class v

fol-

lows from its temporal share t

of the considered time period T, Fig. 4-18. If now