Галусарьян Р.Т. Сборник задач и упражнений по курсу Высшая математика, ч. I
Подождите немного. Документ загружается.

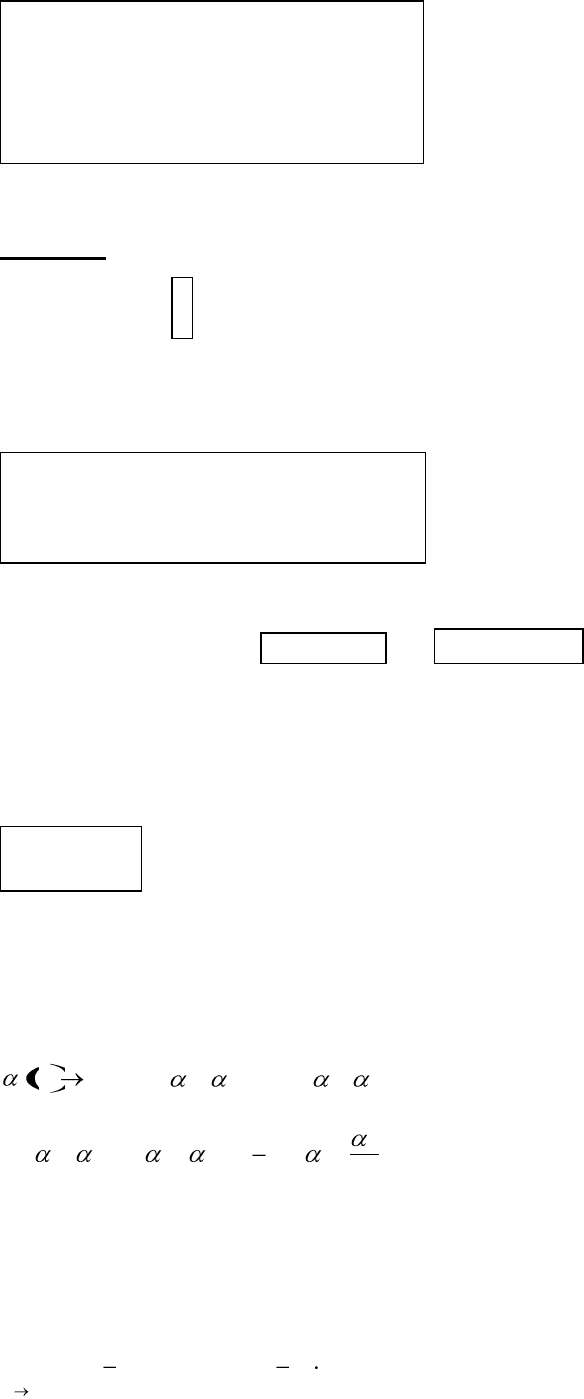
Теорема. Предел отношения двух бесконечно малых
(неопределенность ) равен пределу отношения двух других бесконечно
малых, эквивалентных данным, т.е.
.
Отметим также: если , то .
Основные формулы эквивалентности бесконечно малых.
Первый замечательный предел
Первая группа формул эквивалентности
0х
~,~arcsin arctg
,
2
~cos1,~,~sin
2
tg
Вторя группа формул эквивалентности
eUUUU
aa
U
log)1(~log,1~
ln
1
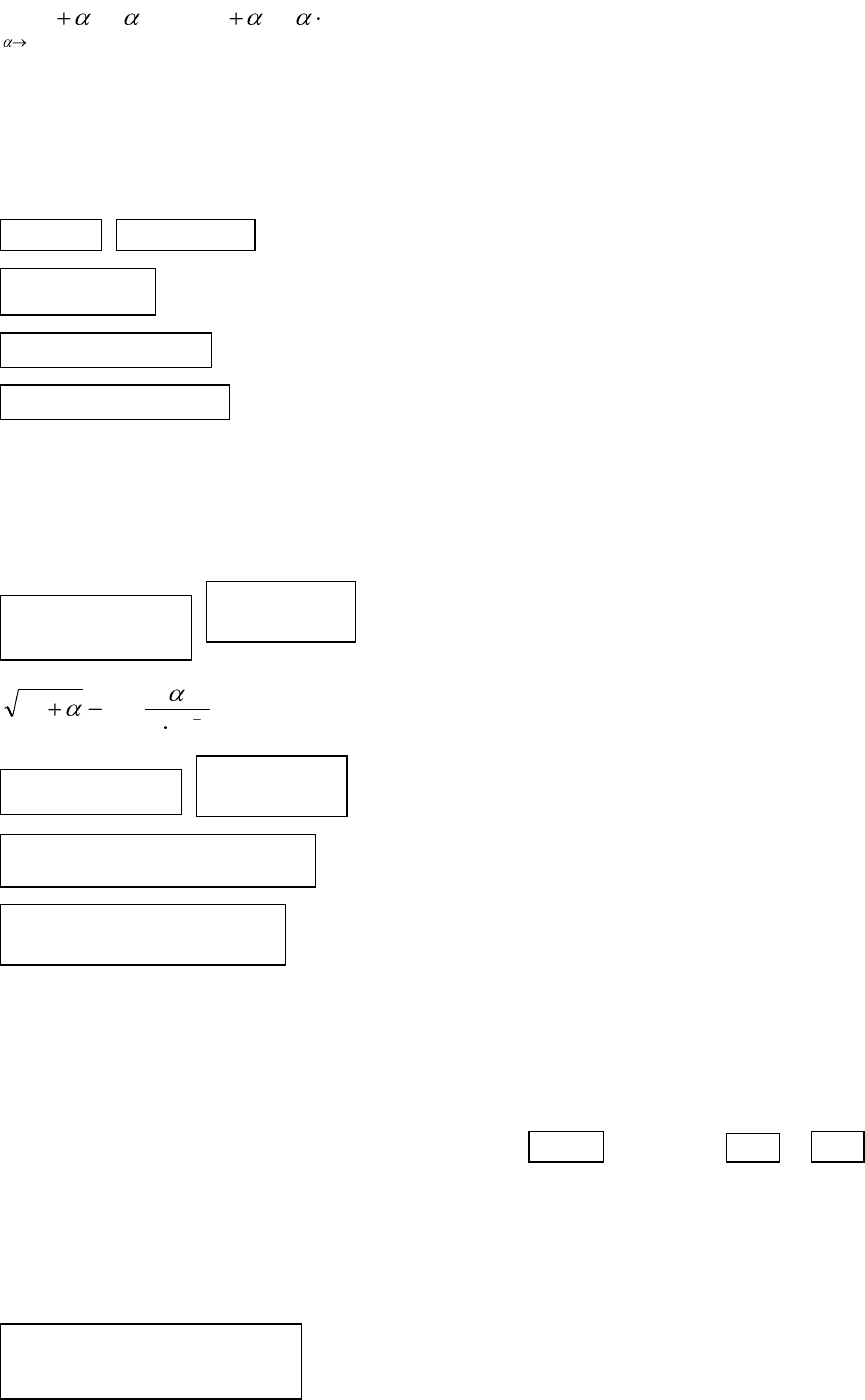
e
aa
log~)1(log,~)1(
ln
0
Третья группа формул эквивалентности
,
,
Четвертая группа формул эквивалентности
,
1
~
k
k
k
ak
aa
,
Все эти четыре группы формул составляют таблицу эквивалентных
бесконечно малых.
Сравнение бесконечно малых. Пусть при функции и
являются бесконечно малыми. Две бесконечно малые называются
сравнимыми, если существует предел их отношения
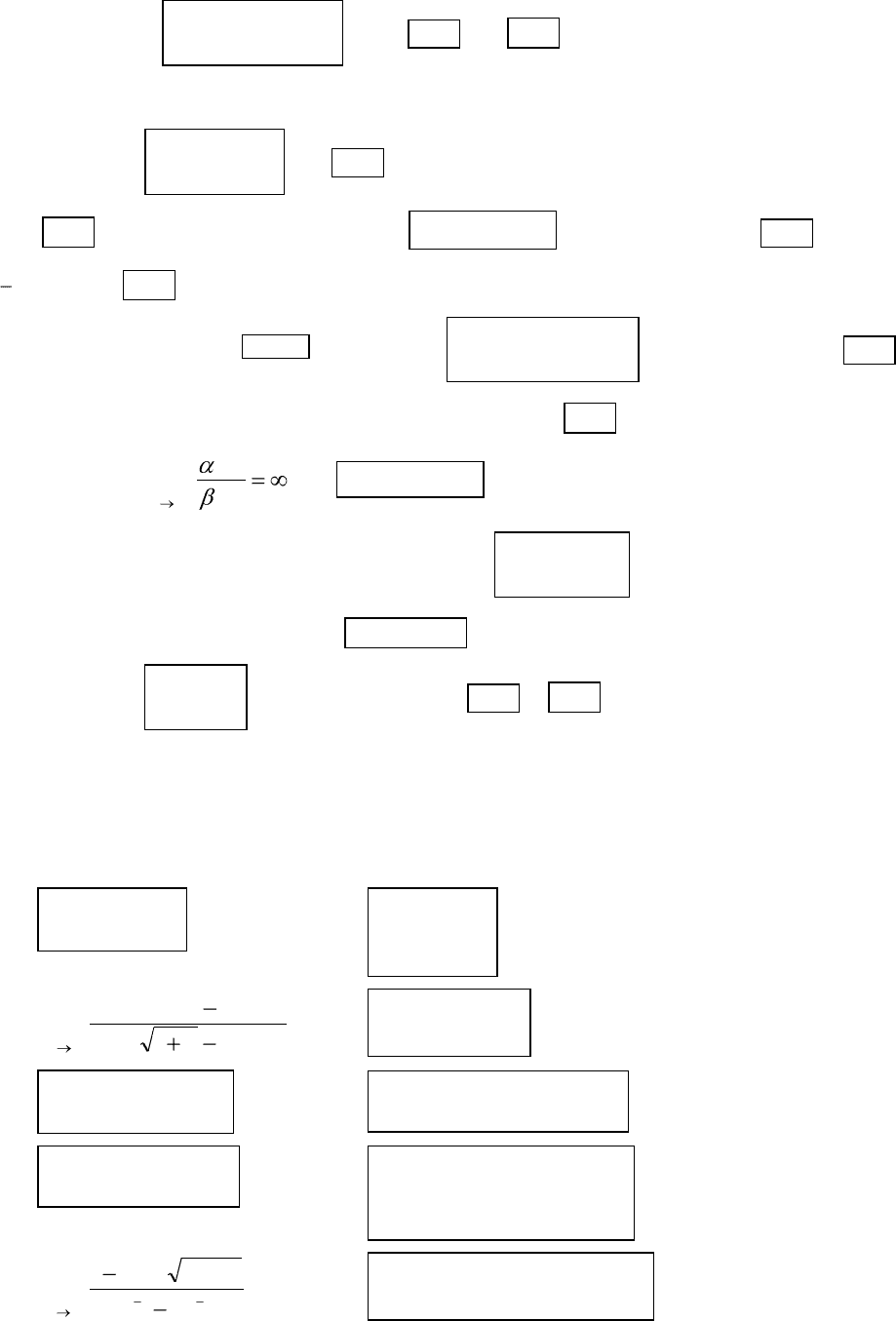
При этом могут быть следующие случаи:
1. Если , то и бесконечно малые одного
порядка.
2. Если , то бесконечно малая более высокого порядка,
чем . Это записывается так: . Читается так: равно
о малое от .
При этом, если такое, что , то говорят, что
есть бесконечно малая порядка “k” относительно .
3. Если
)(
)(
lim
0
x
x
xx
, то .
4. Как уже было сказано выше, если , то бесконечно малые
называются эквивалентными : .
5. Если не существует, то и не сравнимые.
Упражнения к § 2.3
Найти пределы, используя эквивалентность бесконечно малых.
2.111.
2.112.
2.113.
2
5
22
0
)11(
253arcsin2
lim
x
xtgx
x
2.114.
2.115.
2.116.
2.117.
2.118.
2.119.
11
0
2
2coscos1
lim
x
x
ee
xx
2.120.
2.121.
2.122.
2.123.
2.124.
2.125.
2.126.
2.127.
2.128.
2.129.
2.130.
2.131.
2.132.
2.133.
2.134.
2.135.
2.136.
2.137.
2.138.
2.139.
a
x
tg
ax
ax
22
sin
lim
2.140.
2.141.
2.142.
2.143.
2.144.
2.145.
2.146.
2.147.
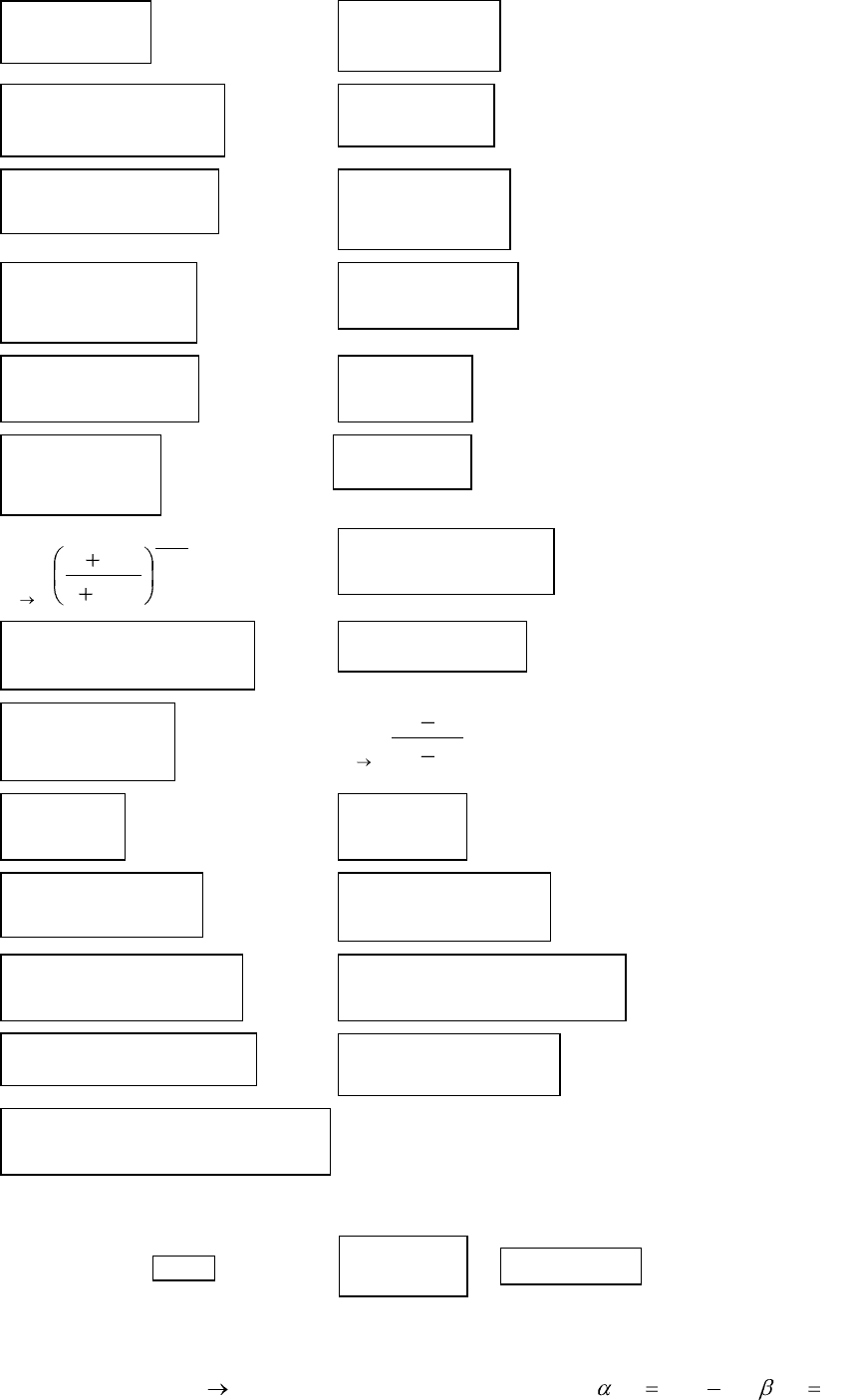
2.148.
2.149.
2.150.
2.151.
2.152.
2.153.
2.154.
2.155.
2.156.
2.157.
2.158.
2159.
2.160.
x
x
x
tgx
3
sin
1
0
sin1
1
lim
2.161.
2.162.
2.163.
2.164.
2.165.
ax
xa
ax
ax
lim
2.166.
2.167.
2.168.
2.169.
2.170.
2.171.
2.172.
2.173.
2.174.
2.175. При функции и бесконечно малые.
Сравните их.
2.175 (а). При
0x
сравнить бесконечно малые
1
sinxx
x
и
xx
.
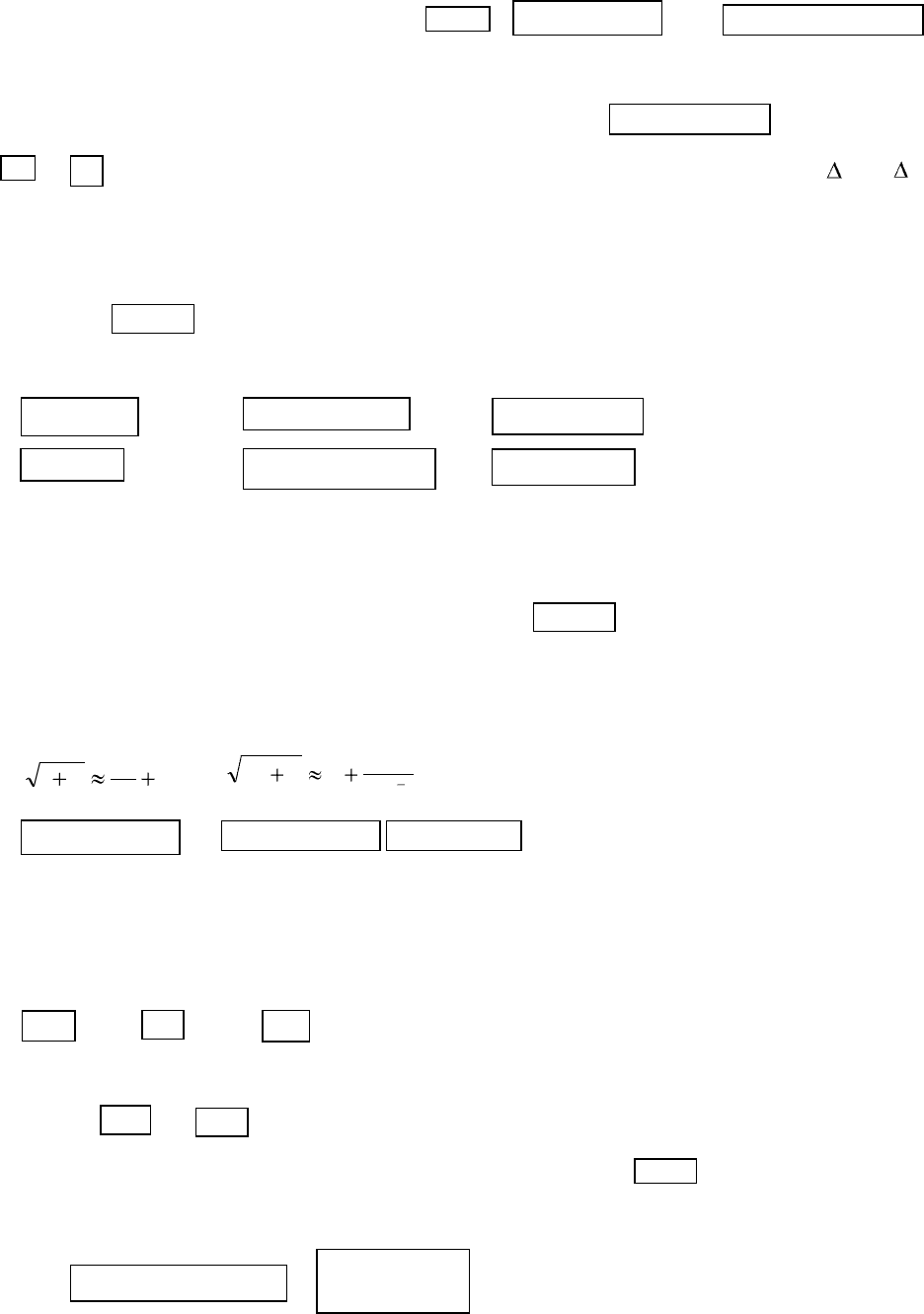
2.176. Доказать, что при и
эквивалентные бесконечно малые.
2.177. Дана функция y=x
3
. Доказать, что при приращения
и бесконечно малые одного порядка. При каком значении x
x
и
y
эквивалентные?
2.178. Определить порядок малости относительно x следующих
функций :
а) ,
б) ,
в) ,
г) ,
д) ,
е) .
2.179. Пользуясь таблицей эквивалентных бесконечно малых, вывести
формулы для приближенных вычислений с точностью до членов
второго порядка (x
2
)
а)
1
2
1
2
x
x
б)
1n
n
n
na
x
axa
в)
г)
С помощью полученных формул приближенно вычислить:
1) ,
2) ,
3) ,
4)
3
04,1
,
5) , 6) .
2.180. Доказать эквивалентность функций (при ):
и .
§2.4 Непрерывность. Точки разрыва. График функции
1. Непрерывность функции (определения)
1. Функция y=f(x) называется непрерывной в точке
)(
0
yDx
, если
предел в точке x
0
равен значению функции в этой точке, т.е.
0
0
( ) ( )
lim
xx
f x f x
2. На языке это означает: для
)(0
такое, что неравенство
)()(
0
xfxf
выполняется для всех х, для которых верно неравенство
0
xx
3. Если и , то f(x) непрерывна в точке x
0
, если
0
0
lim
x
f
, т.е. бесконечно малому приращению аргумента соответствует
бесконечно малое приращение функции.
4. На практике удобно пользоваться следующим критерием. Для
непрерывности функции y=f(x) в точке x
0
необходимо и достаточно, чтобы
1)
)(
0
yDx
, т.е. существовало значение f ( x
0
);
2) существовали односторонние пределы и ;
3) все эти три числа равны между собой, т.е.
2. Понятие о точках разрыва и их классификация
Различают три типа точек разрыва.
1) Точки устранимого разрыва
Односторонние пределы существуют и равны между собой, но не
совпадают со значением функции или значение функции не существует, т.е.
0 0 0
0 0 ,f x f x M но f x M
0
или f x не существует
.

2) Точки разрыва 1-го рода (конечный разрыв)
Односторонние пределы конечные, но не равные ,
называется скачком функции в точке х
0
.
3) Точки разрыва 2-го рода (бесконечный разрыв)
Если хотя бы один из односторонних пределов равен бесконечности
или не существует, то х
0
точка разрыва 2-го рода. Все вышесказанное
относится к точке х
0
, не являющейся границей области определения
функции. Если х
0
граница области определения, то в этой точке
рассматривается односторонняя непрерывность.
3. Об асимптотах графика функции
Напомним, что асимптота прямая линия, к которой бесконечно
приближается график функции при удалении в бесконечность, т.е. асимптота,
как бы касательная, для которой точкой касания является бесконечно
удаленная точка.
Вертикальная асимптота
Известно, что если
0
()
lim
xx
fx
, то
0
xx
вертикальная асимптота.
Следовательно, каждой точке бесконечного разрыва соответствует
вертикальная асимптота. Если оба односторонних предела равны
бесконечности, то асимптоту будем называть двусторонней; если же только
один односторонний предел равен , то асимптоту будем называть
односторонней.
Горизонтальная асимптота
Если
()
lim
x
f x c
, то
су
горизонтальная асимптота. При этом, если
( ) ( )
lim lim
xx
f x f x c
, то
су
будем считать двусторонней асимптотой, а если
()
lim
x
f x c
или
()
lim
x
f x c
, то
су
будем считать односторонней (правой или
левой) асимптотой.
Наклонная асимптота
y kx b
Параметры (k,b) наклонной асимптоты, если она существует,
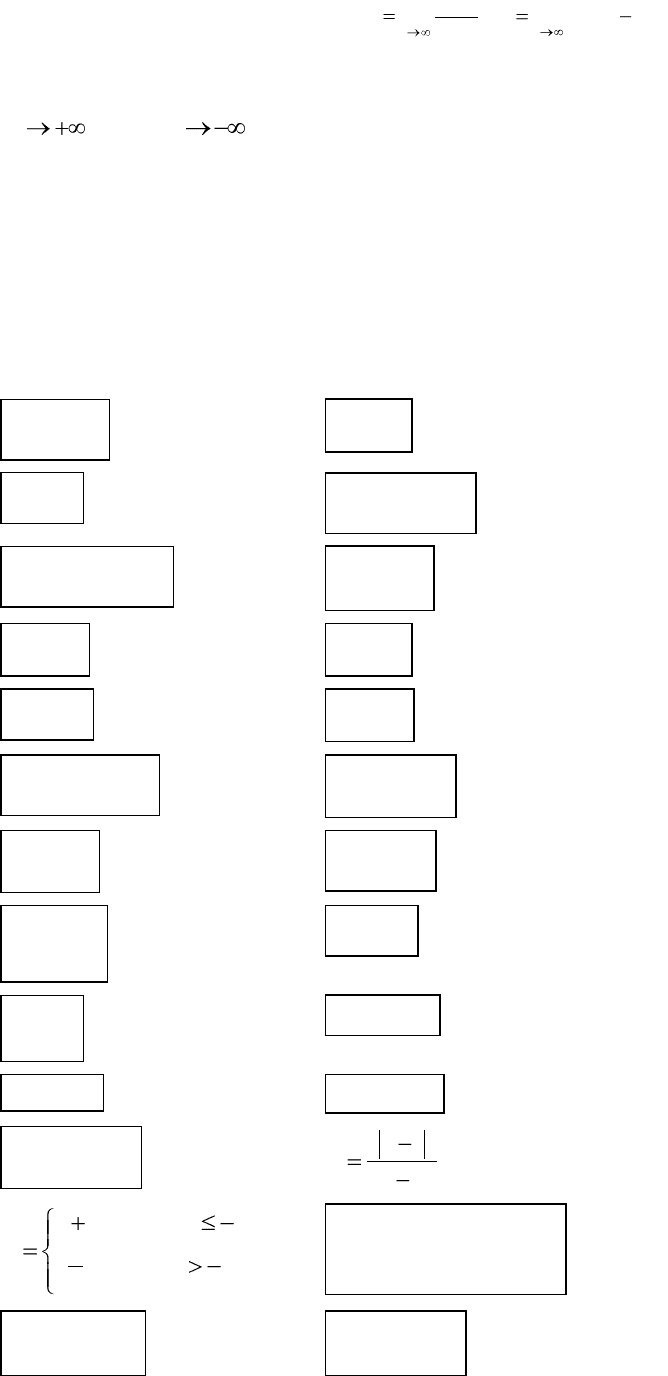
определяются по формулам:
()
lim
x
fx
k
x
,
()
lim
x
b f x kx
.
И здесь, в зависимости от того, существуют ли рассмотренные пределы
при
x
или
x
функция может иметь одну или две асимптоты
(левую и правую).
Упражнения к § 2.4
Исследовать на непрерывность и построить графики функций (2.181-
2.210).
2.181.
2.182.
2.183.
2.184.
2.185.
2.186.
2.187.
2.188.
2.189.
2.190.
2.191.
2.192.
2.193.
2.194.
2.195.
2.196.
2.197.
2.198.
2.199.
2.200.
2.201.
2.202.
32
1
xx
x
y
2.203.
1,
1
1,3
xесли
x
xеслиx
y
2.204.
2.205.
2.206.
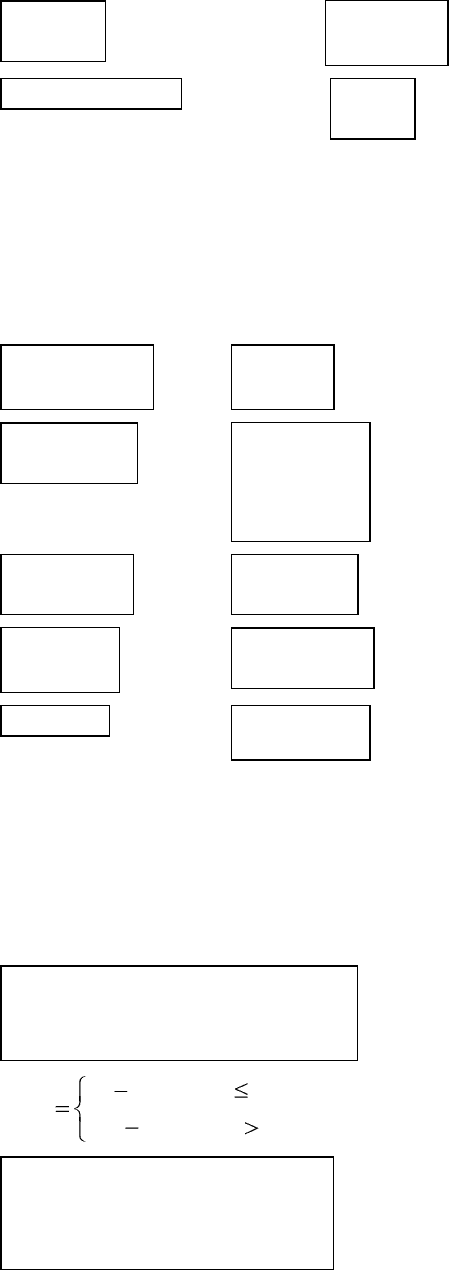
2.207.
2.208.
2.209.
2. 210.
В задачах (2.211-2.220) найти точки разрыва и устранить разрыв, если
это возможно.
2.211.
2.212.
2.213.
2.214.
2.215.
2.216.
2.217.
2.218.
2.219.
2.220.
В задачах (2.221-2.226) подобрать параметры так, чтобы функция была
непрерывной.
2.221.
2.222.
12
1,1
)(
2
xnpuax
xприx
xf
2.223.
