Галусарьян Р.Т. Сборник задач и упражнений по курсу Высшая математика, ч. I
Подождите немного. Документ загружается.

2 3 2
1 2 3 4
2 4 3
1 2 3 4
4 8 7 1
1 2 3 4
x x x x
x x x x
x x x x
.
№11. Найти фундаментальную систему решений (ФСР) системы
однородных уравнений
20
1 2 3 4 5
3 2 2 0
1 2 3 4 5
8 3 3 3 0
1 2 3 4 5
x x x x x
x x x x x
x x x x x
.
§ 1.2 Примерное содержание рейтинговых контрольных работ в
первом семестре
Контрольная работа №1 по теме: «Элементы аналитической геометрии
и линейной алгебры»
Вариант № 0
1. Даны вершины треугольника
,2,2A
6,0B
,
2,3C
. Через середину
АВ проведен перпендикуляр к АВ. Найти точку пересечения его со стороной
ВС. 2. Найти координаты центра, полуоси, фокусы, директрисы гиперболы
01991864916
22
yxyx
.
3. Даны векторы
,1,6,3a
,54 kjib
12,4,3c
.
Найти векторное произведение
()a b c
.
4. Составить уравнение плоскости, проходящей через две параллельные
прямые
2
1
2
3 z
y
x
и
21
1
2
1 zyx
.
5. Решить матричное уравнение
BXA
, если
8
7
0
7
2
3
10
10
1
,
0
4
3
1
2
2
2
3
1
BA
.
6. Проверить систему линейных уравнений на совместность.
Решить методом Жордана
2 4 1
1 2 3
8 3 2
1 2 3
23
13
x x x
x x x
xx
7. Найти общее решение системы неоднородных уравнений
2 3 2
1 2 3 4
2 4 3
1 2 3 4
4 8 7 1
1 2 3 4
x x x x
x x x x
x x x x
Контрольная работа №2 по теме: « Предел. Непрерывность»
Вариант № 0
Найти пределы:
1.
1
42
8
7
lim
2 15
x
x
x
x
.
2.
3
1
1
lim
12
x
x
xx
.
3.
0
93
lim
ln 1
x
tgx
ex
.
4.
2
2
0
1 sin 1
lim
24
x
x
xx
.
5.
5
4
44
2 2 2
16 5 1
lim
1 2 9
x
xx
x x x
.
6. Сравнить бесконечно малые:
1x
.1,ln xxxх
7. Построить график функции (указать точки разрыва):
а)
2
1
9
2;
x
y
б)
1
1
y arctg
x
.
Контрольная работа № 3 по теме: «Производная»
Вариант № 0
Найти первую производную функций (1-3)
1.
5
32
1
1
x
xxy
. 2.
8
2
3
1
n1
x
y
arctg e
.
3.
x
x
xxy cos1
3
sin
2
.
4. Найти первую и вторую производную функции, заданной
параметрически
22
ln 1 , arcsin 1x t y t
.
5. Найти первую и вторую производную неявной функции

2
sin 0x y x y
.
6. Для функции
2
cos1
2
x
xy
по формуле Лейбница найти
6
y
.
7. Для функции
6
1
2
xx
y
найти
n
y
.
§ 1.3 Методы построения графиков функций
Графики некоторых функций
Если данную функцию можно представить в виде суммы элементарных
функций, то график можно построить методом сложения графиков
слагаемых функций.
Пример 1. Построить график функции
2
3
1
x
x
y
.
Решение. Представим функцию в виде суммы
2
1
x
xy
.Строим
графики слагаемых функций
2
21
1
,
x
yxy
.
На рис.2 они изображены пунктирными линиями.

Графики функций
1
y
и
2
y
пересекаются в одной точке (1; 1). Так как
при
0,00
21
yyx
, то
121
yyyy
и
2
yy
и, следовательно, при
0x
график данной функции расположен ниже графиков слагаемых
функций. При
0,00
21
yyx
и, следовательно, график данной функции
расположен между прямой
xy
1
и гиперболой
2
2
1
x
y
. График пересекает
ось OX в точке ( 1;0). При
x
график асимптотически приближается к
прямой
xy
1
. При
0x
(справа) график приближается к ветви гиперболе
2
2
1
x
y
. При
0x
(слева) график приближается к вертикальной
асимптоте
0x
и ветви гиперболы, оставаясь между ними. При
x
график приближается к прямой
xy
1
.
Методом сложения графиков построим графики гиперболических
функций.
Пример 2. Гиперболический синус
2
xx
ee
shxy
.
Решение. Имеем:
),()(),,()( yyD
.
)(
2
)( xy
ee
xy
xx
нечетная функция. Shx принимает любые значения,
причем sh0 =0 (рис.3).
Пример 3. Гиперболический косинус
2
xx
ee
сhxy
.
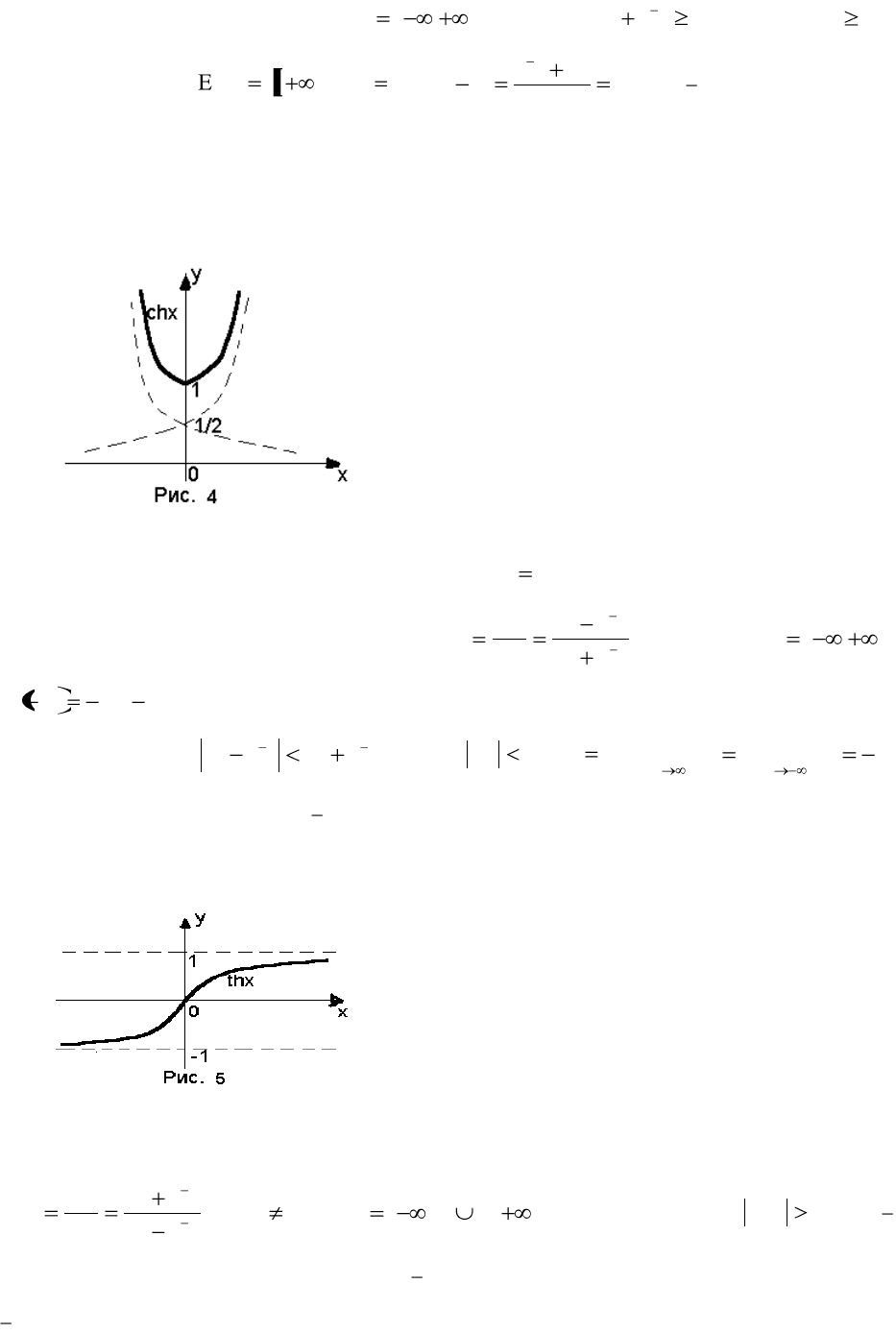
Решение. Имеем:
),()(yD
. Т.к.
2
xx
ee
, то
1сhx
и,
следовательно,
.10),,1)( chy
)(
2
)( xy
ee
xy
xx
четная функция
(рис.4).
Пример 4. Гиперболический тангенс
thxy
.
Решение. Имеем:
xx
xx
ee
ee
chx
shx
thx
.
),()(yD
,
thxxth
нечетная функция.
Так как
xxxx
eeee
, то
00.1 ththx
.
1lim,1lim thxthx
xx
.
Следовательно, y = 1 и y = 1 – горизонтальные асимптоты (рис.5).
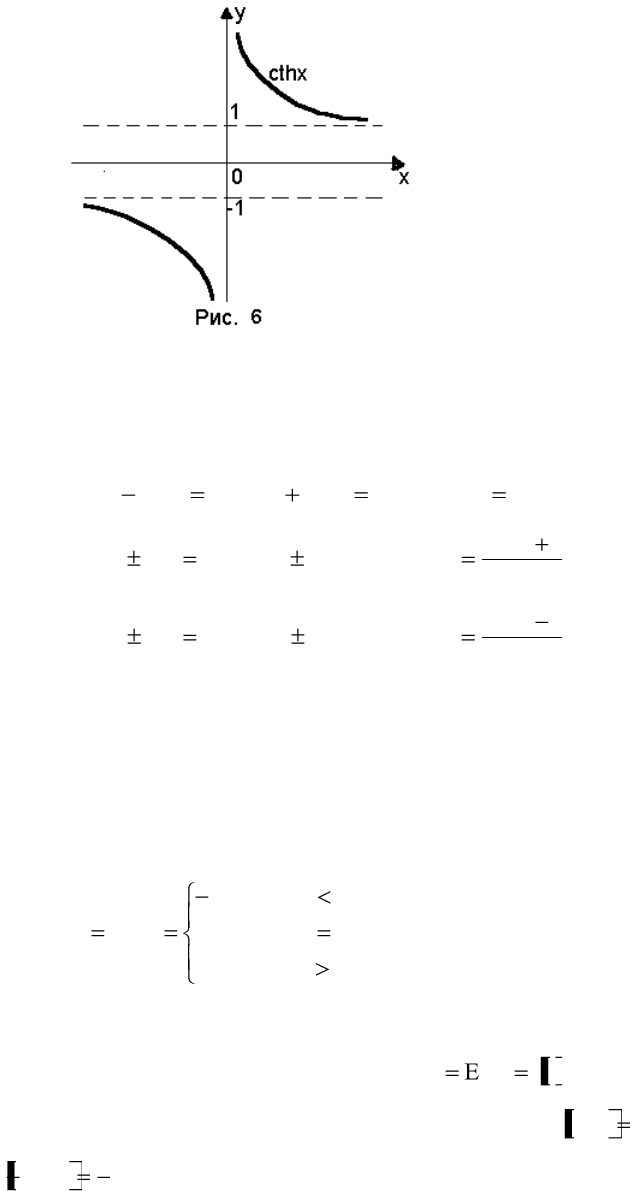
Пример 5. Гиперболический котангенс y = cthx. Решение. Имеем:
xx
xx
ee
ee
shx
chx
cthx
.
),0()0,()(,0 yDx
. Очевидно,
thxccthx ,1
нечетная функция. y = 1 и y = 1 – горизонтальные асимптоты, x = 0
вертикальная асимптоты. График представлен на рис.6.
Отметим формулы, связывающие гиперболические функции
,22,2,1
2222
shxchxxshxchxshxchxshxch
2
12
,)(
2
212121
xch
xchshxchxch xshxxxsh
2
12
,)(
2
212121
xch
xshshxshxchxchxxxch
Некоторые функции, примыкающие к элементарным
1. Функция сигнум (знак)
0если,1
0если,0
0если,1
sgn
x
x
x
xy
2. Целая часть числа (антье):
xxy )(
. Это наибольшее целое число,
не большее данного (рис 8). Отметим, что
234,2
, т.к. 2,34 = 2 + 0,34,
334,2
, т.к. –2,34 = - 3 + 0,66.
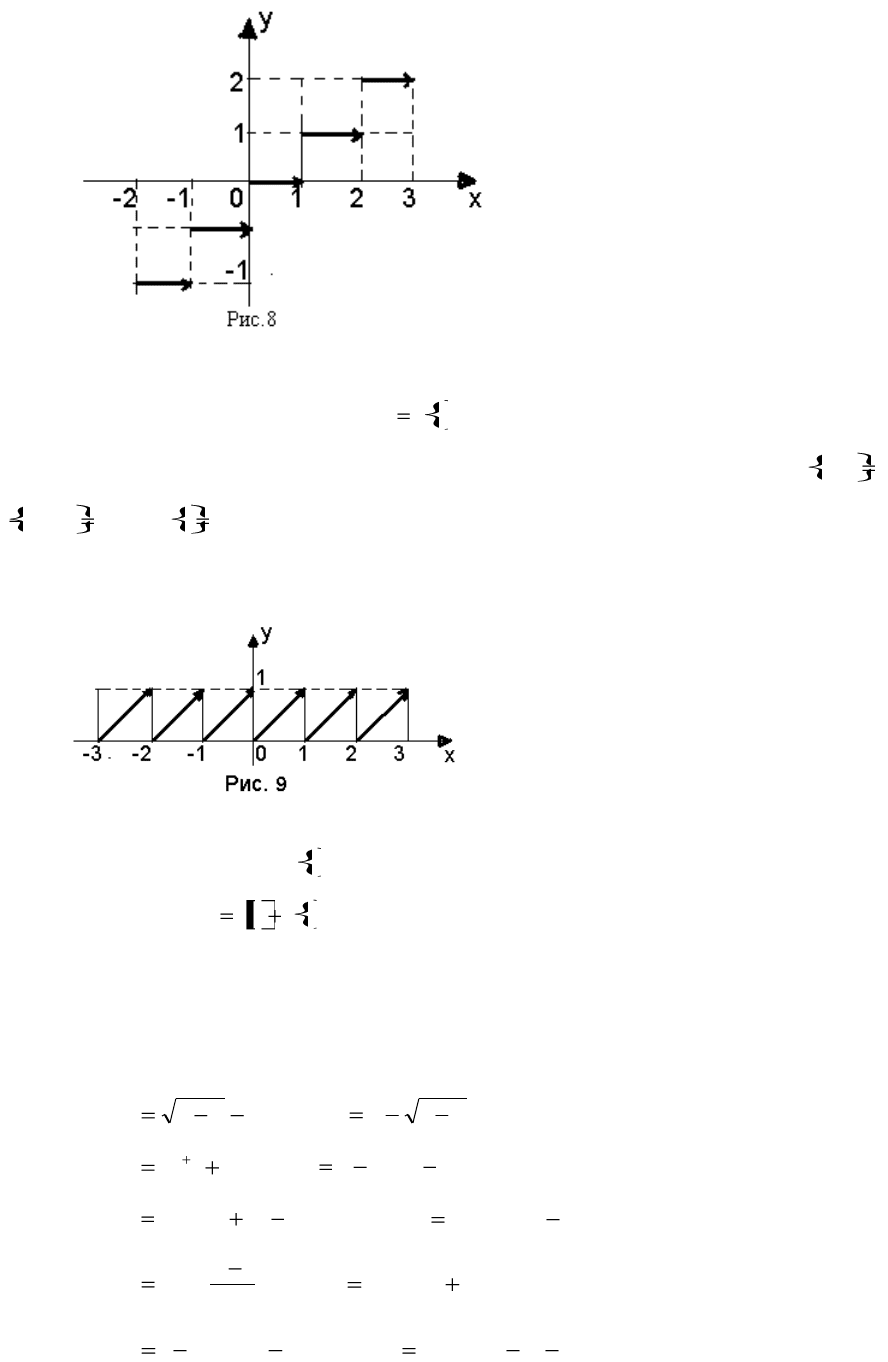
3. Дробная часть числа
xy
(рис 9.). Напомним, что дробная часть
числа есть неотрицательное число, меньшее единицы:
34,034,2
,
66,034,2
,
02
.
Дробная часть
x
– периодическая функция с периодом Т =
1.Очевидно, что
xxx
.
Упражнения к § 3
Построить графики функций
3.1.
,24
3
xy
3.2.
,32 xy
3.3.
,12
3x
y
3.4.
),(log3
2
xy
3.5.
,1)3(log
2
xy
3.6.
),3arcsin(2 xy
3.7.
,
2
1
cos3
x
y
3.8.
),23sin(2 xy
3.9.
),2(1 xarctgy
3.10.
,1)arccos(2 xy
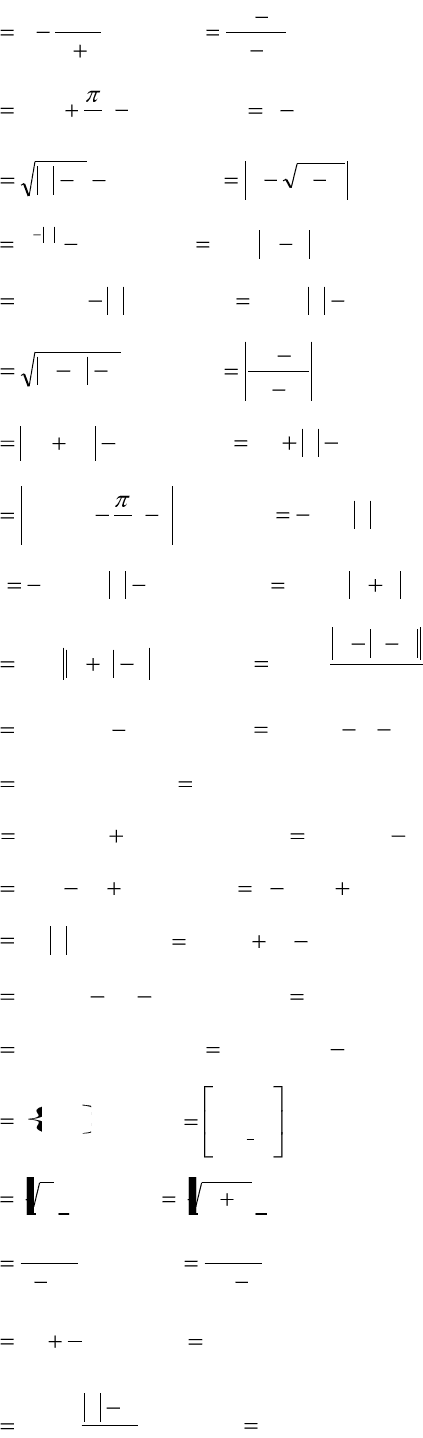
3.11.
,
1
4
2
x
y
3.12.
,
2
23
x
x
y
3.13.
,2)
4
(xtgy
3.14.
,21 xctgy
3.15.
,21
3
xy
3.16.
,32 xy
3.17.
,32
x
y
3.18.
,3log
2
xy
3.19.
),2(log
2
xy
3.20.
),1(log
2
xy
3.21.
,12xy
3.22.
,
2
23
x
x
y
3.23.
,23
2
xxy
3.24.
,6
2
xxy
3.25.
,1)
4
cos(2 xy
3.26.
,sin2 xy
3.2.7.
),3arcsin( xy
3.28.
,2arcsin xy
3.29.
,31log
3
xy
3.30.
,
3
12 x
arctgy
3.31.
),2(log
2
3
xxy
3.32.
),2(log
2
2
xxy
3.33.
,sin
2
xy
3.34.
,cos
2
xy
3.35.
,)1arccos(
2
xy
3.36.
,)1arcsin(
2
xy
3.37.
,3)2(xthy
3.38.
),2(1 xshy
3.39.
,xcthy
3.40.
,2)3(2 xchy
3.41.
),6sgn(
32
xxxy
3.42.
),sgn(cos xy
3.43.
),sgn(lg xy
3.44.
),1sin2sgn( xy
3.45.
,cos xy
3.46.
,log
3
1
xy
3.47.
,xy
3.48.
,2
3
xy
3.49.
,
1
1
2
x
y
3.50.
,
1
2
x
x
y
3.51.
,
1
2
x
xy
3.52.
),2arccos(cos xy
3.53.
,
3
2
arcsin
x
y
3.54.
),cos(arccosxy
3.55.
),sin(arccos xy
3.56.
),4sgn(
2
xxy
3.57.
,
sgnx
xy
3.58.
,
3
xy
3.59.
),cos(sgn xarctgy
3.60.
).sgn(log
3
2
xxy
3.61. | x – y | + | x + y | = 1, 3.62. | x + 2y | + | x – 2y | = 2.
3.63. y = {
x – 1
/
3
} , 3.64. y = {
3 – x
/
2
} .
3.65. min ( x, y ) = 1, 3.66. max ( x, y ) = 1.
3.67. min ( x
2
, y ) = 1, 3.68. max ( | x |, | y | ) = 1.
3.69. min ( x, y
3
) = 1, 3.70. max ( x + y, x - y) = 1.
