Галуев Г.А. Математическая логика и теория алгоритмов

Подождите немного. Документ загружается.

Математическая Логика и Теория Алгоритмов стр. 51 из 64

Конфигурация однозначно определяет работу МТ. Пусть

- конфигурации

некоторой МТ z, а Р,R- произвольные последовательности символов на ленте. МТ пе-

реходит из

()

→ в одном из трех случаев

1. по команде

jlki

qxxq

. В этом случае символ

x в рабочей ячейке заменяется

x , состояние

q заменяется состоянием

q , а лента остается без движения

RxPq

, xlRPq

2. по команде

jki

lqxq

. Лента передвигается на одну ячейку влево, состояние

меняется на

q , RxPq

, RqP

3. по команде

jki

rqxq . Лента передвигается на одну ячейку вправо, состояние

q заменяется на

xlRqPx

xlRxPq

Конфигурация

называется заключительной, если не существует такой кон-

фигурации

, что

→

Вычислением в МТ называется последовательность

конфигураций l,,...,,

таких что

→

,…,

l→

, где l - заключительная конфигурация.

Анализ и синтез машин Тьюринга

Проблема анализа МТ состоит в том, чтобы для данной МТ определить на каждом

шаге её реакцию на заданное входное слово т.е. в построении вычисления в МТ. Про-

ведем такой анализ на примере конкретной МТ.

Например: Пусть МТ задана таблицей Тьюринга

000

lqxq 5.

001

lqxq

020

lqxq 6.

021

lqxq

110

lqxq 7.

2212

qxxq

211

rqxq

Заметим, что эту же МТ можно задать с помощью таблиц Айзермана

XQ\

Табл. 4

Или обобщенной таблицей

XQ\

q lxq

lxq

rxq

lxq

sxq

Табл. 5

Пусть на ленте записано входное слово

1011201

xxxxxxx и МТ находится в началь-

ном состоянии

q , а головка находится против самого левого символа входного слова

(т.е. против

x ). Процесс анализа (т.е. процесс вычисления) записывается следующи-

ми конфигурациями:

Математическая Логика и Теория Алгоритмов стр. 52 из 64

10112010

xxxxxxxq

10112011

xxxxxxqx

10112001

xxxxxqxx

10110201

xxxxqxxx

10111201

xxxqxxxx

10112201

xxxxqxxx

10122201

xxxxqxxx

В последней (7) конфигурации у нас появляется (согласно инструкции

2212

qxxq ) ситуация

xq для которой у нас нет команды. Поэтому анализируемая МТ

на этом шаге останавливается (заменяет

на

и формирует ситуацию

для ко-

торой нет команды).

Пусть теперь входное слово будет

221

xxx , тогда процесс вычисления примет

вид:

.....

0221

2021

2211

дтиBBqxxx

Bxqxx

xxqx

xxxq

т.к.

xB = , то согласно первой инструкции из примера 1 (т.е.

000

lqxq ) МТ будет рабо-

тать бесконечно и никогда не остановится (т.к. лента бесконечна).

Рассмотрим теперь сущность проблемы синтеза МТ и идею проведения синтеза

МТ на примере так называемых числовых МТ. В таких машинах алфавит состоит из

двух символов:

В-пробела и | (палочки, черточки). Произвольные целые числа представимые в

числовой МТ

кодируются унитарным кодом, следующим образом: |||,...2||,1|,0 === (чер-

та сверху означает кодированное число).

Построим простейшую МТ, вычисляющую сумму x+y любых двух целых неотри-

цательных чисел. На ленту занесем сначала первое число x, а затем через пробел В

второе число у. Вычисление начнем с крайней левой позиции, предположив, что МТ

находится в начальной ситуации

. Будем считать, что результат получен, если на

ленте осталось столько палочек, записанных не обязательно подряд, чему равно зна-

чение суммы. Это значение таково:

−

yxyx . Для построения МТ используем

следующую процедуру. Сначала выделим первую палочку кода

и стираем ее. Затем

выделяем первую палочку кода

и тоже стираем ее. В результате на ленте остает-

ся число палочек равное сумме х+у. При это заметим, что этот же результат можно

получить и другим способом(например, стирая не первые а последние палочки в ко-

дах

и так далее ). Исходя из этой идеи можно синтезировать множество ко-

манд, определяющих требуемую МТ. Действительно по команде

Blqq МТ перейдет из

начальной ситуации в рабочее состояние

q , а в рабочей ячейке появится первая па-

лочка кода

. Далее по команде

| Bqq эта палочка стирается и машина переходит с

ситуацию

. По команде

Blqq

машина МТ сдвинет ленту влево и перейдет в ситуа-

Математическая Логика и Теория Алгоритмов стр. 53 из 64

цию |

q . После команды

| lqq в рабочей ячейке будет пробел В предшествующий

коду

. Тогда по команде

Blqq приходим к ситуации |

q . Команда

| Bqq сотрет

первую черточку кода

. В итоге мы построим следующую таблицу Тьюринга:

Blqq 3.

Blqq 5.

Blqq

| Bqq 4.

| lqq 6.

| Bqq ,

которая задает МТ выполняющую сложение чисел в унитарном коде.

Лекция 10.

Диаграммы Тьюринга.

Рассматривая выше пример синтеза числовой МТ, мы получили таблицу Тью-

ринга, включающую 6 команд, описывающих простейшие операции по просмотру

массива унитарного кода и стиранию двух его элементов. При выполнении более

сложных операций число команд таблицы существенно возрастает, что усложняет

процесс синтеза МТ. Для облегчения синтеза МТ используют композицию элементар-

ных МТ. Набор

элементарных МТ как правило ограничен и все они имеют фиксиро-

ванную систему команд. Если каким-нибудь образом обозначить элементарные МТ и

указать связи между ними, то результат их композиции будет представлять собой

диаграмму Тьюринга (ДТ).

Пусть

},...,,{

10 n

xxxX = - входной алфавит, r, l – сдвиг ленты соответственно вправо и

влево, S –стоп,

x или В пробел,

- множество слов над Х, А – слово в алфавите Х.

Будем считать, что двухбуквенный алфавит Х состоит из В и | (черточка). Бу-

дем обозначать через ~ произвольную последовательность букв, несущественную в

данном контексте, а через ~ - несущественную в данном контексте букву. Пусть ↑

указывает букву, которую в данном шаге просматривает считывающая головка

МТ.

С учетом сказанного можно привести несколько примеров элементарных МТ:

а) МТ

x . Примененная к произвольной позиции, печатает в рабочей ячейке букву

x .

Очевидно, что таблица Тьюринга для этой машины имеет вид:

100

qxxq

. . . . . . . .

qxxq

б) МТ r. Примененная к произвольной позиции, сдвигает ленту на одну ячейку вправо

и останавливается.

в) МТ l. Аналогичная МТ со сдвигом влево.

Для МТr и МТl имеем таблицу Тьюринга:

100

rqxq

100

lqxq

. . . . . . . . . . . . . .

rqxq

lqxq

г) МТ, выполняющая трехкратный сдвиг ленты вправо и печать на ней буквы

100

rqxq

302

rqxq

. . . . . . . . . . . . . . . .

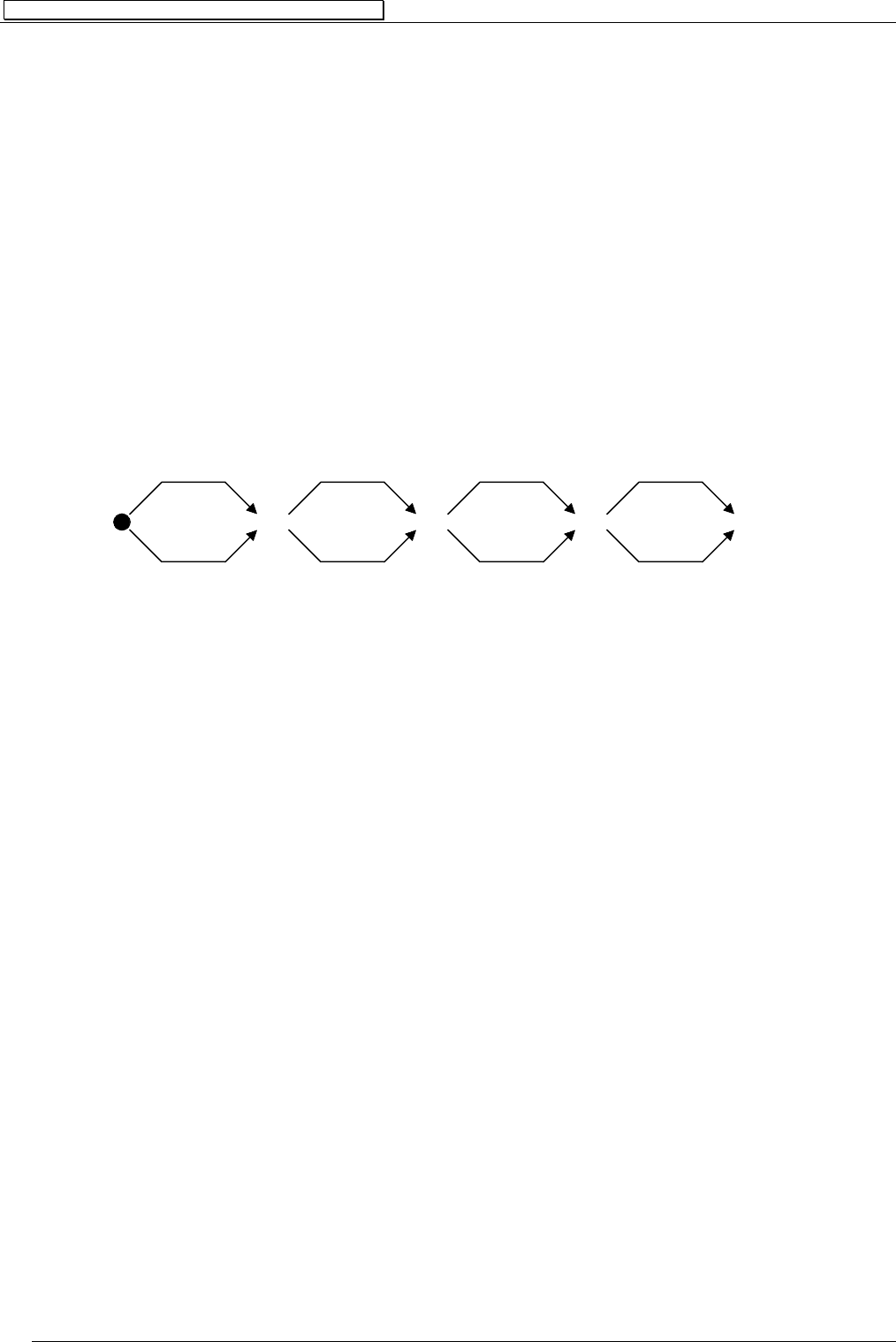
Математическая Логика и Теория Алгоритмов стр. 54 из 64

rqxq

201

rqxq

4003

qxxq

. . . . . . . . . . . . . . . .

rqxq

403

qxxq

Машины

lrx

,, примем за элементарные МТ. Тогда, например, МТ пункта г)

можно собрать из трех машин r и машины

)0(

Пусть

MM ,...,

некоторые элементарные МТ с общим алфавитом Х. Диаграмма

МТ включает помимо символов элементарных машин символ • (точка) и стрелки,

взвешенные(помеченные) буквами алфавита Х. Причем символ • (точка) может встре-

чаться в ДТ только один раз (он определяет начало работы), а из любого символа

машины может выходить не более одной стрелки

, помеченной одной и той же буквой.

Тогда можно заменить таблицу Тьюринга для(например) МТ из

г) следующей диаграммой

Изображение диаграмм можно упростить следующим образом . заменим все

стрелки для всех j=0,1,…,n одной стрелкой без букв. Если среди всевозможных стре-

лок для всех j=0,1,…,n отсутствует лишь некоторая, взвешенная (помеченная) буквой

, то заменяем все стрелки одной, указав над ней

≠

. опустим точку, если она со-

единена всеми стрелками только с одним символом. Опустим непомеченные стрелки

между двумя символами и будем писать

вместо

MMM ...

−

.(n раз). Тогда, ука-

занная выше ДТ примет вид

Из такого способа построения ДТ следует, что переход от таблицы Тьюринга к

ДТ осуществляется однозначно. Для этого требуется выполнить следующие условия:

заменить каждый символ элементарной МТ соответствующей ей таблицей; ввести пе-

реобозначение состояний в командах всех элементарных машин; ввести сквозную

нумерацию в полученной обобщенной таблице.

Машины Тьюринга и вычислимые функции.

Пусть задана некоторая МТz с состояниями

qqq ,...,,

и натуральный ряд чисел

N (включая ноль). Поставим в соответствие каждой

),...,,(

21 n

aaakn − , где

niNa

,...,2,1, =∈ некоторую конфигурацию

aaaq ...

2101

. Если для МТ существует вы-

числение, начинающееся в конфигурации

и доходящее до заключительной конфи-

гурации

,...,,:

, то число

Np ∈

, сопоставляемое

, есть значение функции от

z и начальной n-ки, то есть

),...,,(

21 nz

aaap

= . Если не существует такого числа р, что

конфигурация

является заключительной, то функция

не определена для рас-

сматриваемой n-ки и МТz работает бесконечно. Таким образом, исходя из МТz, мы

пришли к функции с областью определения на множестве

(или может быть на не-

Математическая Логика и Теория Алгоритмов стр. 55 из 64

котором подмножестве

), где

- множество всевозможных упорядоченных n-ок из

Будем исходить теперь из функций, определенных на

или его подмножест-

ве. Функция f определенная на некотором подмножестве множества

, является

частично вычислимой, если существует МТz, такая, что для всякой n-ки

),...,,(

21 n

xxx ,

которой соответствует некоторое значение f, выполняется равенство

),...,,(),...,,(

2121 nzn

xxxxxxf

Функция f называется вычислимой, если она определена на всем множестве

и является частично вычислимой.

Примером вычислимой функции является функция f(x,y)=x+y, поскольку ранее

мы для нее построили МТ, вычисляющую значение f(x,y) для любых x и y.

Геделевский номер машины Тьюринга.

Пусть

PPP ,...,,

соответственно первое, второе и так далее к-ое простое число.

Из теории чисел известно, что любое натуральное число n (положительные целые

числа n=1,2,…) можно представить в виде

PPPn *...**

( то есть в виде произведения простых чисел),

где

aa ,...,

- целые неотрицательные числа, включая ноль.

Например,

100000

13*11*7*5*3*213 =

112

5*3*260 =

Очевидно, что для любого n однозначно определяется набор

aa ,...,

и, наобо-

рот по любому набору

aa ,...,

однозначно восстанавливается соответствующее ему

число n. Если для произвольного слова в некотором алфавите ввести определенным

образом числовое кодирование входящих в него букв, то для данного слова можно

найти однозначно определяющее его число n , которое по сути дела будет являться

его числовым именем. В, частности, каждой команде или набору команд, задающих

МТ, можно

сопоставить некоторое целое положительное число. Это число называется

гёделевским номером МТ по имени математика Курта Гёделя, который впервые при-

менил числовое кодирование для обозначения нечисловых объектов в доказательстве

знаменитой теоремы о неполноте арифметики.

Гёдель предложил использовать следующий способ кодирования цепочек. По-

ясним его идею на примере кодирования команд МТ. Пусть задана

команда

211

lqxqQ

Для того, чтобы закодировать эту команду, необходимо ввести кодирование симво-

лов и мест их расположения в команде. Будем кодировать символы нечетными целы-

ми числами большими единицы

...27_25_23_21_19_17_15_13_11_9_7_5_3

...____________

4433221100

qxqxqxqxqxsrl

а номера их мест в команде – простыми числами

1234…k…

2357…

P …

Тогда команде

211

lqxqQ =

будет однозначно соответствовать число

1931315

7532)( ⋅⋅⋅=⋅ Qgn ,

которое и есть гёделевский номер команды Q.

Если задана упорядоченная последовательность команд

QQQQ ,...,,,

321

, которая

задает некоторую МТz, то эта последовательность может быть закодирована следую-

щим числом

)(

)()(

......32)(

Qqn

QqnQqn

PPzgn

⋅

⋅⋅

⋅⋅⋅⋅⋅=⋅ , которое представляет собой гёделевский но-

мер МТz.

Пример.

1001

lqxqQ =

153911

7532)( ⋅⋅⋅=⋅ Qgn

Математическая Логика и Теория Алгоритмов стр. 56 из 64

10112

qxxqQ =

1591315

7532)( ⋅⋅⋅=⋅ Qgn

2013

lqxqQ =

193915

7532)( ⋅⋅⋅=⋅ Qgn

Так как гёделевские номера команд

)3,2,1(

оказались упорядоченными в

соответствии с нумерацией команд, то гёделевский номер МТz равен

1939151591315153911

753275327532

532)(

⋅⋅⋅⋅⋅⋅⋅⋅⋅

⋅⋅=⋅ zgn

Таким образом, каждая МТ получает свой гёделевский номер. Поскольку процеду-

ра приписывания номеров является механической, можно поручить ее некоторой

MTG

. Заметим, что MTG

вычисляет, в частности, и вой собственный геделевский но-

мер ng(G

). Справедливо также и обратное то есть что существует такая МТG

, кото-

рая для любого положительного числа n выдает один из двух ответов:

- n не является геделевским номером никакой МТ

- n является геделевским номером MT

, имеющей следующие команды…

Отметим, что если G

, получает на вход число n=ng(G

), то оно выдает ответ второго

типа и печатает коды своих команд.

Рекурсивные и рекурсивно перечислимые множества

Рассмотрим некоторую функцию f(x

,...,x

) = Ψ

,...,x

). По определению

она частично вычислима, если существует МТz, которая эту функцию вычисляет. Так

как машине Z однозначно сопоставлен геделевский номер z = ng(z), то всякой час-

тично вычислимой функции f(x

,...,x

) можно сопоставить геделевский номер имен-

но той МТ. Которая эту функцию вычисляет. Введем функцию Фz(x

,...,x

) (где z –

целое неотрицательное число, а (x

,...,x

) – некоторая n-ка из N

) следующим об-

разом. Если z = ng(z), причем z это МТz, вычисляющая значения f на n-ке

,...,x

), то значение функции Фz(x

,...,x

) совпадают со значением функции

f(x

,...,x

). Если z не является геделевским номером никакой МТ, то значение

функции Фz(x

,...,x

) = 0. В результате мы получим вычислимую функцию и можем

теперь записать последовательность Ф

, Ф

, …,Ф

, … Которая перечисляет (быть мо-

жет с повторением) множество частично вычислимых функций от n аргументов. Таким

образом мы можем в принципе перечислять области определения частично вычисли-

мых функций.

Пусть заданы теперь произвольные Z и (x

,...,x

). Тогда. Чтобы вычислить

значения функции Фz(x

,...,x

), необходимо сначала вычислить являются ли Z ге-

делевскими номерами какой-либо МТ. Эту задачу решает МТ

, введенная выше. Ес-

ли Z не является геделевским номером. То Фz(x

,...,x

) = 0. в противном случае

МТz, команды которые распечатываются MTG

, предлагается (x

,...,x

) в качестве

исходного задания. Соединяя G

и Z, мы получаем универсальную МТ, вычислитель-

ную функцию Фz(x

,...,x

). Если на ленте этой машины поместить число z = ng(z),

то она сможет вычислить функцию соответствующую этому числу.

Пусть X произвольный элемент множества М и А<М. Характеристическая функ-

ция подмножества А. обозначаемая C

определяется следующим образом

Будем говорить, что множество называется рекурсивным

, если его

⎩

⎨

⎧

∉

∈

Ахесли

)(

Математическая Логика и Теория Алгоритмов стр. 57 из 64

характеристическая функция вычислима. Если множество рекурсивно, то существует

МТ, которая, получив на вход элемент этого множества, всегда ставит ему в соответ-

ствие некоторый ответ: либо 1, либо 0. (т.е.

AxлибоAx

∉

∈

Будем говорить, что множество называется рекурсивно-перечислимым, если

оно является областью определения некоторой частично вычислимой функции. Тео-

ретически можно перечислить частично-вычислимые функции от 1,2 и т.д. целочис-

ленных переменных. Следовательно в принципе мы умеем перечислять и рекурсивно

перечислимые множества Г

, Г

, …, Г

,…

С учетом сказанного имеет место следующая

: Множество является ре-

курсивным тогда и только тогда, когда оно само и его дополнение рекурсивно пере-

числимы.

Эта теорема по сути дела утверждает, что любое рекурсивное множество рекур-

сивно перечислимым. Однако она оставляет открытым вопрос о

том, любое-ли множе-

ство является рекурсивным. Далее мы покажем, что существуют множества некото-

рые являются рекурсивно перечислимыми, но не являются рекурсивными.

Неразрешимость проблемы остановки для

произвольных машин Тьюринга.

Сформулируем следующую проблему: существует ли МТ, для которой входны-

ми заданиями являются пары (Z,X) (где z = ng(z), а x-произвольное натуральное

число), такая, что при поступлении на вход МТz исходных данных Х она отвечала-бы:

либо «да, МТz применима к Х, т.е. начав вычисление с Х, выдает некоторый результат

и остановится», либо «нет, предлагать

МТz задание Х не следует, т.к. она никогда не

остановится». (в этом случае говорят что МТ не применима к Х). Эта проблема из-

вестна под названием проблемы остановки для произвольных машин Тьюринга. Су-

ществует теорема.

. Проблема остановки для произвольных машин Тьюринга

алгоритмически

неразрешима.

Для доказательства этой теоремы покажем сначала, что существуют множества,

которые являются рекурсивными.

Рассмотрим множество машин Тьюринга, вычисляющих функции от одного ар-

гумента. Каждой их этих машин Z будем предлагать качестве исходного задания ее

собственный геделевский номер z = ng(z). Если машина Z остановится и выдаст неко-

торый результат, то будем называть ее несамоприменимой.

Таким образом, на мно-

жестве всех машин мы определим некоторую функцию от Z, которая очевидно, час-

тично вычислимая функция. Для нее можно построить конкретную МТ, вычисляющую

этой функцию. Для этого необходимо построить сначала универсальную МТ, вычис-

ляющую значения этой функции для любых чисел. В результате множество G геде-

левских номеров самоприменимых машин будет

рекурсивно-перечислимым множест-

вом.

Предположим теперь, что множество G является рекурсивным. Это равносильно

рекурсивной перечислимости его дополнения Ğ. В таком случае должна существовать

МТ, перечисляющая Ğ в перечислении рекурсивно перечислимых множеств

, Г

, …, Г

,…

Предположим, что множество Ğ имеет в этом перечислении номер λ. Поэтому

запишем Ğ=Г

. Тогда для любого натурального Х

∈

Ğ ↔ Х

∈

(↔ знак логической эк-

вивалентности). Однако из определения самоприменимости следует Х

∈

Ğ ↔ Х

∈

где Г

– множество самоприменимых машин, имеющих в перечислении Г

, Г

, …, Г

,…

номер х. Отсюда вытекает Х

∈ Г

↔ Х

∉

х.

Если теперь положить Х = λ, то имеем Х

∈

↔ Х

∉Г

. Полученное противоречие доказывает, что множество G не является рекур-

сивным. Итак, действительно, не всякое множество, являющееся рекурсивно пере-

числимым является и рекурсивным.

Предположим теперь, что существует машина Т. Которая для произвольной па-

ры (z,x) решает проблему остановки. Пусть G – рекурсивно перечислимое, но не ре-

Математическая Логика и Теория Алгоритмов стр. 58 из 64

курсивное множество. Множество G есть область определения некоторой частично

вычислимой функции f(x)=Ψ

(x), вычисляемой МТz . Тогда машина Т – для любого

натурального числа х даст один из 2-х ответов: «да, Х

∈

G и Z остановится» либо «нет

∉ Ğ и Z никогда не остановится». Это означало бы что G рекурсивное, а не рекур-

сивно перечислимое множество, что противоречит принятому предположению. Полу-

ченное противоречие доказывает теорему.

Нетрудно видеть, что существует аналогия между универсальной машиной Тью-

ринга и универсальной ЭВМ. В этом случае проблема остановки приобретает следую-

щий смысл. Пусть имеется некоторая

программа Z и исходные данные Х, которые

вводятся в ЭВМ. Спрашивается: существует–ли такая общая программа Р, которая по-

зволяет заранее выяснить, остановится-ли ЭВМ начав вычисление по программе с

входными данными Х, или не остановится? На основании доказанной выше теоремы

мы теперь знаем, что ответ будет отрицательным. Подобной программы Р не

сущест-

вует. Это означает, что никогда не будет написана программа, с помощью которой

можно было бы обнаруживать в произвольных программах ошибки, приводящие к

бесконечным вычислениям. Важно отметить, что понятия вычислимости и рекурсив-

ности эквивалентны. Понятие вычислимости ввел А. Тьюринг, а понятие рекурсивно-

сти – С. Клини оба этих понятия были введены

с целью формализовать интуитивное

представление о вычислимости и алгоритме. Примечательно; что все другие понятия,

введенные с той же целью А. Черчем (Л - конверсии), Э.Постом (комбинаторные про-

цессы), А.Марковым (нормальные алгоритмы) оказались эквивалентными друг другу.

Это позволило Черчу сформировать свой знаменитый тезис о том, что введение поня-

тия правильно формализуют

интуитивное представление об алгоритме и вычислимо-

сти и, что их нельзя обобщить. Поэтому из всех эквивалентных понятий можно выби-

рать одно и отождествлять его с одним из точных определений алгоритма и на его ос-

нове строить некоторую теорию.

Комбинаторные системы и машины Тьюринга

Покажем теперь, что можно построить машину Тьюринга в которой любое вы-

числение, приводящее к конечному результату, соответствует выводу некоторой тео-

ремы в комбинаторной системе и наоборот. Пусть имеется некоторое входное слово n,

заданное унитарным кодом

. Если предложить машине Z в качестве исходного зада-

ния

, то начав вычисление с конфигурации nq

, машина либо выдаст результат, ли-

бо будет работать бесконечно. Будем считать, что МТz заключает все промежуточные

результаты вычислений между двумя маркерами h.

Паре (Z, n) поставим в соответствие по полутуэвскую систему П с аксиомой

h Подстановки в системе П выберем таким образом, чтобы ее промежуточные

формулы соответствовали промежуточным конфигурациям МТz, а заключительная

формула hsh – заключительной конфигурация МТz, означающей, что соответствую-

щее вычисление завершено. Имеет место следующая теорема.

Теорема. Если МТz

с начальным состоянием q применимо входному слову n, то это

эквивалентно тому, что в полутуэвской системе П с аксиомой h

h выводима форму-

ла hsh.

При доказательстве этой теоремы ограничимся только доказательством того

факта, что если МТz, применимо к n , то из этого следует что в полутуэвской системе

П выводима формула hsh. Обратное доказательство справедливо, но приводить его не

будем.

Покажем как по командам МТz можно построить систему П. Алфавит системы П

образуется объединением

входного алфавита, алфавита состояний МТz и маркера h.

Аксиомой системы П является начальная ситуация (состояние) МТz

с маркерами h

слева и справа, то есть h

h. Команде МТz q

в системе П сопоставляется под-

становка Pq

Q→Pq

Q, которая обеспечивает переход от конфигурации, которая

Математическая Логика и Теория Алгоритмов стр. 59 из 64

имела место в МТz до применения команды, к конфигурации в которую переходит МТz

после применения команды. Здесь P и Q некоторые слова (контекст). Команде q

соответствует подстановка Px

Q→Pq

Q. Команде q

соответствует подстанов-

ка Pq

Q→Px

Кроме того введем в систему П дополнительные подстановки, которые не соот-

ветствуют никаким командам МТz и применяются только тогда, когда МТz переходит

в заключительную конфигурацию и останавливаются (в этом случае МТz встретилась

с ситуацией q

, которой нет ни в одной команде или выполнила команду q

Подстановки hPq

Qh→hPq

Qh, которые для всех пар (q

), не встречающихся в ле-

вых частях команд МТz, заменяют символ состояния q

маркером q. Подстановки

hPqx

Qh→hPqQh стирающие все символы (кроме h) справа от q. Подстановки

hPqh→hPsh вводит символ S слева от правого h. Подстановки hPx

sh→hPsh стирают

все символы между левым h и s. И наконец подстановки hx

...x

0sh

→ hsh, которые пе-

ремещают левый маркер h в позицию предшествующую символу S.

Пока МТz выполнит вычисления над числами n в соответствии с командами, на-

чиная с аксиомой h

h , формируется вывод в полутуэвской системе П по принципу:

одна применяемая команда МТz один шаг вывода в системе П. Как только МТz остано-

вилась, к полученной формуле системы П применяются дополнительные (введенные

выше) подстановки, которые в конечном итоге приводят к формуле hsh. Таким обра-

зом теорема доказана.

Заметим что в системе П

от числа n зависит только аксиома n nq

h, алфавит

подстановки не зависит от n. Если n принимает значение из множества целых не от-

рицательных чисел, то действуя таким образом как указано в доказательстве теоре-

мы, мы получим семейство полутуэвских систем П, с помощью этого семейства мно-

жеству тех чисел n, с которым применима МТz , ставиться в соответствие единст-

венная формула hsh. Это

позволяет построить систему П, которая, исходя из аксиомы

hsh, выдавала бы в качестве заключительных формул все целые числа к которым

применима МТz. Для этого необходимо в качестве аксиомы выбрать hsh, а в качестве

системы подстановок взять подстановки обратные, обратные подстановкам системы

П. Тогда, если объединить системы П и

′

(при этом в качестве аксиомы такой объе-

диненной системы взять hsh), то легко видеть, что МТz будет соответствовать туэв-

ская система Т. Построенные комбинаторные системы П,

′

и Т, соответствующая

МТz, сопоставляют входным словам машины Z формулы в указанных системах. Вы-

брав в качестве МТz такую машину для которой неразрешима проблема остановки,

мы приходи к выводу что в соответствующих полутуэвской и туэвской системах не-

разрешима проблема доказуемости. Это же справедливо для нормальных постовских

систем, что еще раз доказывает

справедливость тезиса Черча об эквивалентности

различных утонченных понятий алгоритма.

Как уже отмечалось раннее теория алгоритмов явилась основой для создания

современной вычислительной математики и во многом обусловило появление ЭВМ и

алгоритмических языков для их программирования. Рассмотрим более подробно со-

временные понятия алгоритмов, алгоритмического языка и программы и покажем их

связь с рассмотренными

нами на протяжении ряда лекций основами теорий алгорит-

мов.

Лекция 11.

Взаимосвязь теории алгоритмов и современной информати-

ки

Современное понятие алгоритма. Свойства алгоритмов.

Основные результаты, полученные в рамках рассмотренной нами теории алго-

ритмов, позволяет перейти от интуитивного понятия алгоритма к его полному опреде-

Математическая Логика и Теория Алгоритмов стр. 60 из 64

лению. В настоящее время понятию алгоритма, соответствует определение. Вклю-

чающее следующие категории:

1. Алгоритм есть конечная совокупность инструкций

2. Есть некоторый механизм, воспринимающий и исполняющий инструкции.

3. Имеются средства, позволяющие хранить и фиксировать сведения о всех эта-

пах работы алгоритма, хранить промежуточные результаты и выдавать их по

мере необходимости.

4. Все

выполняемые алгоритмом действия являются дискретными.

5. Последовательность операций из которых сформирован алгоритм является де-

терминированной и в каждом шаге выполняется единственным образом.

Если алгоритмы предназначены для реализации на ЭВМ, то это определение не-

обходимо вести ограничение, накладываемые особенностями использования компью-

тера.

Возможным вариантом таких ограничений является следующий:

1. Алгоритм – А

оперирует с конкретными объектами. Эти объекты можно пере-

нумеровать.

2. А- задается конечным аргументом выходным и рабочим алфавитом.

3. В- должно быть составлено таким образом, чтобы определяемый им операции

выполнялись поэтапно.

4. В- должно быть составлено так, чтобы оно исполнялось однозначно.

5. В- должно быть исполнимо то есть применение А к

одному и тому же слову

должно приводить к одним и тем же последовательностям действий и резуль-

татам

6. В- должно быть составлено так, чтобы его исполнение не требовало информа-

ции, отличной от имеющейся во входном слове.

7. Нет никаких ограничений на длину В, длину слов и число шагов. Важно толь-

ко, чтобы они были конечными.

8. Для исполнения В требуется сколь угодно большая, но конечная память.

В целом алгоритм можно описать множеством других определений, например,

через конструктивно задеваемое соответствие в некотором алфавите, через понятие

частичного алгоритма и т.д.

Будем называть алфавитным отображением или оператором всякое соответст-

вие сопоставляющее словам некоторого

алфавита слово в том же алфавите. При на-

личии двух алфавитов первый называется входным, а второй выходным. Алфавитный

оператор называют однозначным, если он ставит в соответствие одному слову вход-

ного алфавита не более одного слова выходного алфавита. Совокупность всех вы-

ходных слов с которыми работает оператор, называется областью его определения.

Эта область может быть конечной или бесконечной. В этом случае оператор задается

в виде таблицы, во втором системой правил. Эта система должна быть конечной и за-

давать соответствие за конечное число шагов.

В алфавитном отображении (операторе) важным является понятие соответст-

вия, а не способа, которым это соответствие задано. В понятии же

алгоритма главным

является способ задания соответствия. Таким образом, это алфавитный оператор

вместе с правилами, определяющими способ его (оператор) выполнения.

Частичным алгоритмом называется

совокупность конечного числа шагов –

команд, выполняемых механически за конечное время и с оцениваемыми конечными

затратами. Примером частичного алгоритма является программа ЭВМ.

: Алгоритмом называется такой частичный алгоритм, который по-

сле конечного числа шагов либо исчерпывает все команды и выдает результат, либо

выдает информацию о невозможности поучения результата.

Всевозможные уточнения приведенных и других определений алгоритма как ока-

залось, являются эквивалентными. В соответствии с упоминавшимся уже ранее тези-

сом Чёрча имеем: