Галуев Г.А. Математическая логика и теория алгоритмов

Математическая Логика и Теория Алгоритмов стр. 31 из 64

Пусть

{

}

,...1

,...,

n

AAA = - эрбрановский базис множества

S

.

H

- интерпретацию

I

удобно представлять в виде множества

{}

,...,...,,

21 n

mmmI = , где

i

m есть или

i

A или

j

A

для

...,2,1

=

i

.

Смысл этого множества в том, что если

i

m есть

i

A , то элементарной формуле

i

A присвоено значение 1, в противном случае – 0

Интерпретацию множества дизъюнктов

S

не обязательно задавать над эрбра-

новским универсиумом. Пусть, например

{}

),(,(),( ayfyQxPS = .

Тогда возможна следующая интерпретация

I

над областью

{}

2,1=D

:

1)2(;0)1(

;0)2,2(;0)2,1(;1)1,2(;1)1,1(

;2)2,2(2)2,1(2)1,2(;1)1,1(;2

==

====

=

===

PP

QQQQ

ffffa

Можно определить

H

-интерпретацию

*

I

, соответствующую любой интерпрета-

ции

I

.

Для рассмотренного выше примера эрбрановский базис

S - таков

{}

...)),,(),,((),),,(()),,(,(),,((),,(),( aafaafQaaafQaafaQaafPaaQaPA =

Оценим теперь каждый член

A , используя заданную интерпретацию

I

:

...

0)2,2()),(),,((

0)2,2()),,((

0)2,2())2,2(,2()),(,(

1)2())2,2(()),((

0)2,2(),(

1)2()(

==

===

==

QaafaafQ

QaaafQ

QfQaafaQ

PfPaafP

QaaQ

PaP

Следовательно,

H

- интерпретация

*

I

, соответствующая

I

есть

{}

),...),,(()),,(,()),,((),,(),(

*

aaafQaafaQaafPaaQaPI ⎤⎤⎤= .

О

п

р

е

д

е

л

е

н

и

е

.

Пусть

I

- интерпретация на области D .

H

- интерпретацией

*

I

, со-

ответствующей

I

, является интерпретация, которая удовлетворяет следующим усло-

виям:

Пусть

n

hh ,...,

1

- элементы эрбрановского универсума

H

. Пусть каждый

i

h отобра-

жается в некоторый

i

d в D . Если )...,,(

1 n

ddp получает в интерпретации

I

значение

1(0), то

),....,(

1 n

hhP также получает значение 1(0) в

*

I

.

Очевидно, справедлива следующая лемма.

Лемма 1. Если интерпретация

I

на некоторой области

D

удовлетворяет множе-

ству (является моделью множества) дизъюнктов

S , то любая из −

H

интерпретаций

*

I

, соответствующих

I

, также удовлетворяет S .

Т

е

о

р

е

м

а

а (

о

н

е

в

ы

п

о

л

н

и

м

о

с

т

и

м

н

о

ж

е

с

т

в

а

д

и

з

ъ

ю

н

к

т

о

в

в) Множество дизъюнк-

тов

S

выполнимо тогда и только тогда, когда

S

ложно при всех

H

- интерпретациях в

H

.

Доказательство.

Необходимость.

По определению множество дизъюнктов

S

невыполнимо тогда и

только тогда, когда

S

ложно при всех интерпретациях на любой области, следова-

тельно, и при

H

- интерпретациях на области

H

.

Достаточность

. Предположим, что S ложно при всех

H

- интепретациях. Поло-

жим, что

S выполнимо (имеется некоторая интерпретация

I

, являющаяся моделью S )

. Пусть

*

I

это

H

- интерпретация, соответствующая

I

. Тогда согласно доказанной вы-

ше лемме множество

S истинно в интерпретации

*

I

. Это противоречит нашему пред-

Математическая Логика и Теория Алгоритмов стр. 32 из 64

положению, что S ложно при всех

H

- интерпретациях. Следовательно S должно быть

невыполнимо, что и требовалось доказать.

Таким образом, на основании этой теоремы, для установления невыполнимости

множества дизъюнктов достаточно рассмотреть лишь

H

- интерпретации над эрбра-

новским универсиумом.

Далее мы и будем рассматривать только

H

- интепретации.

Прежде чем переходить к теореме Эрбрана, устанавливающей условия невыпол-

нимости множества дизъюнктов, требуется ввести понятие семантического дерева.

Дерево это граф (т.е. объект, задаваемый упорядоченной парой <

u

x

, >, где

x

-

множество вершин;

u - множество ребер, соединяющих вершины их

x

, причем каж-

дое ребро, направленное от (выходящих из) вершины

i

x к вершине (входящее в вер-

шину)

j

x

, можно задать парой <

ji

xx ,

> не содержащий циклов и имеющий только од-

ну корневую вершину куда не заходит ни одно ребро.

О

1

x

=

1

u <

21

, xx >

2

x О О

3

x

=

2

u <

31

, xx >

О О О О О

=

3

u <

42

, xx >

4

x

5

x

6

x

7

x

8

x .

.

О

п

р

е

д

е

л

е

н

и

е

.

. Пусть

S - множество дизъюнктов и

A

его эрбраноский базис. Се-

мантическое дерево для

S есть растущее вниз дерево (в соответствии с введенным

определением дерева), в котором каждому ребру приписано конечное множество

элементарных формул из

A или их отрицаний таким образом, что:

1. Из каждого угла (вершины)

N

выходит конечное число ребер

N

LL ...,,

1

.

Пусть

Q i- конъюнкция всех литер, приписанных ....,,1 niL

i

= Тогда

n

VQVVQQ ...

21

- общезначимая формула.

2. Пусть для каждого узла

)(NIN

есть объединение всех множеств, припи-

санных ребрам ветви, входящей к узлу

N от корневой вершины. Тогда

)(NI не содержит контрарных пар (Если A -элементарная формула, то го-

ворят, что две литеры

A и

A

¬

контрарны друг другу, а множество

{}

AA ⎤, называют контрарной парой)

О

п

р

е

д

е

л

е

н

и

е

.

. Пусть

{}

...,...,

1 N

AAA = - эрбрановский базис множества S . Говорит,

что семантическое дерево для

S

будет полным тогда и только тогда для каждого i и

каждого конечного узла

N

семантического дерева (т.е. для узла, из которого не вы-

ходит никаких ребер)

)(NI содержит либо

i

A , либо

i

A⎤ .

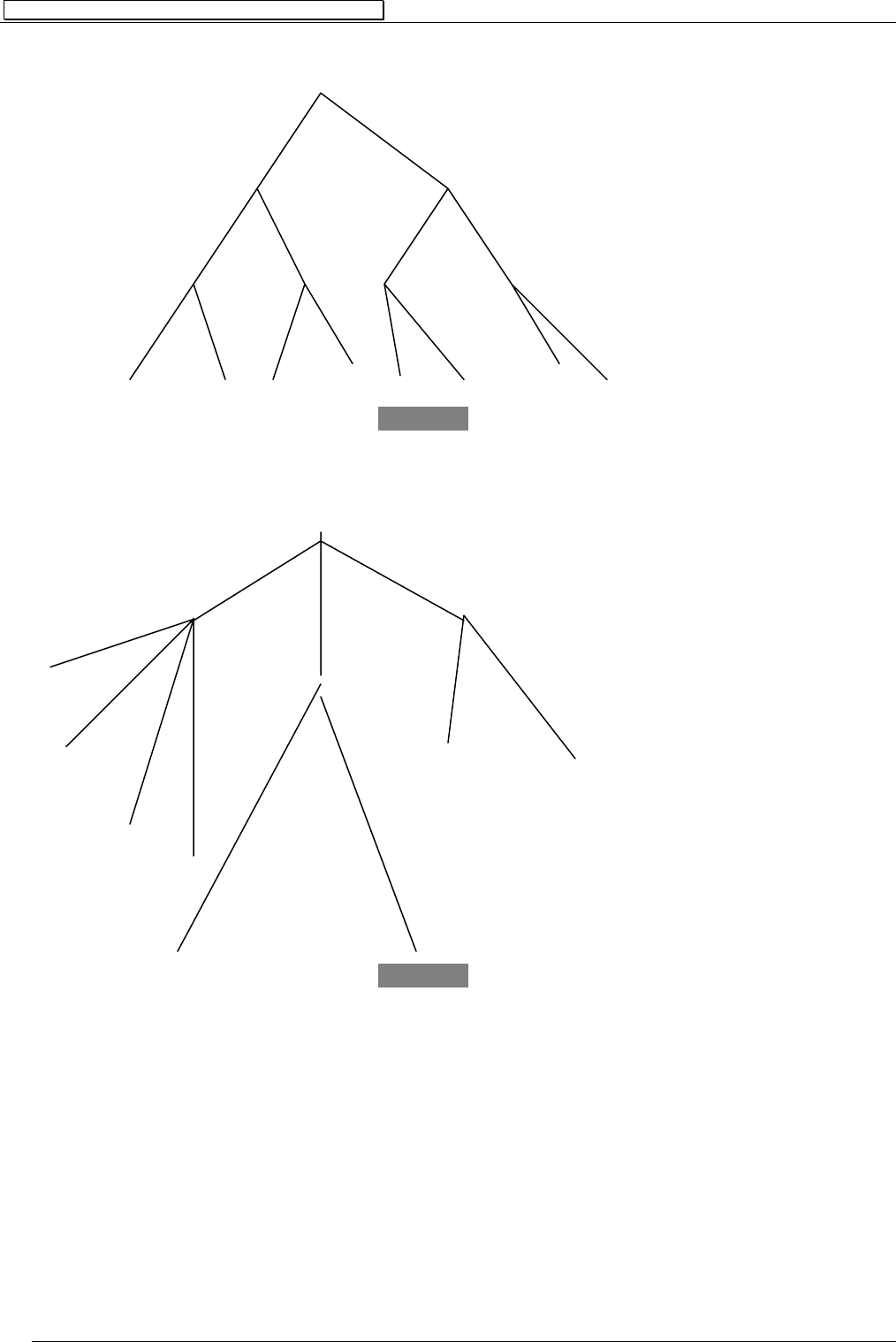
Рассмотрим примеры семантических деревьев.

Пусть

{}

RQPA ,,= - эрбрановский базис множества S . Тогда, например, каждое

из указанных деревьев есть полное семантическое дерево для

S .

Математическая Логика и Теория Алгоритмов стр. 33 из 64

P

О P⎤

О О

Q Q⎤ Q Q⎤

О О О О

R⎤ R⎤

R

R⎤

R

О

R

О О

R

О О О

R⎤

О О

Рис.5 (а)

О

P

QP,⎤

О

PQ ⎤⎤ , О

RQ,

О О

RQ,⎤

R⎤

R

О О О

RQ ⎤⎤ ,

О

RQ ⎤, О

R⎤

О

R

О

Рис.5 (б)

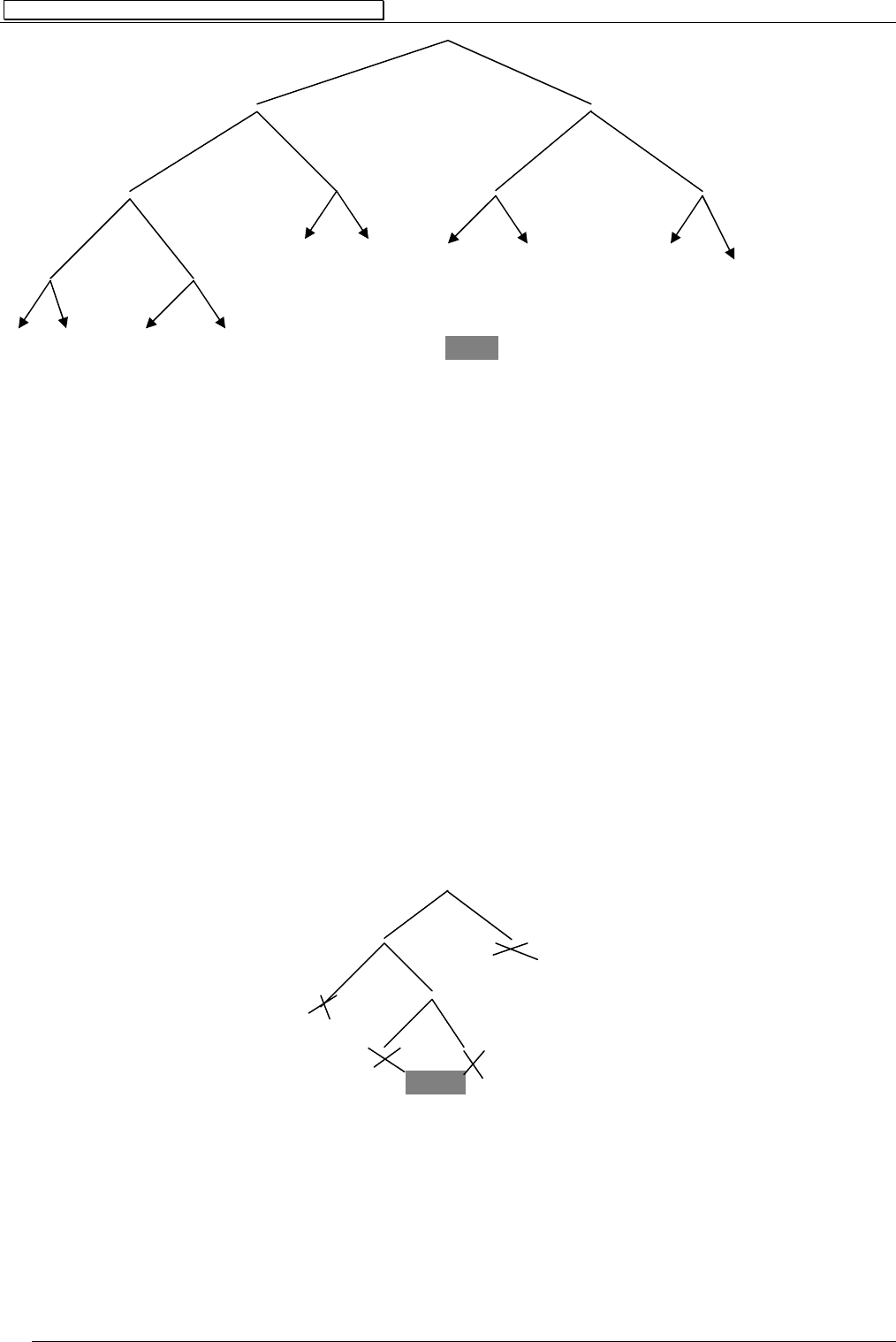
Пусть

{}

))((),( xfQxPS = . Эрбрановский базис множества S есть.

{}

))),...((()),(()),((),(),( affPafQafPaQaP

Семантическое дерево для этого

S

показано ниже.

Математическая Логика и Теория Алгоритмов стр. 34 из 64

О

)(aP )(aP⎤

О О

)(aQ

)(aQ⎤

)(aQ

)(aQ⎤

О О О О

))(( afP⎤ ))(( afP

О О

Рис.6

Заметим, что для каждого узла

N в семантическом дереве для S )(NI есть под-

множество некоторой интерпретации для

S

. Поэтому )(NI будем называть частичной

интерпретацией для

S .

Если эрбрановский базис множества

S бесконечен, то и всякое полное семанти-

ческое дерево для него также будет бесконечно. Очевидно и ясно, что полное семан-

тическое дерево для

S соответствует полному перебору всех возможных интерпрета-

ций для

S .

Введем определения.

О

п

р

е

д

е

л

е

н

и

е

.

. Узел

N называется опровергающим, если )(NI опровергает некото-

рый основной пример дизъюнкта в

S (т.е. этот основной пример дизъюнкта имеет в

интерпретации

)(NI значение 0), но для любого предшествующего

N

узла

'

N )(

'

NI не

опровергает никакого основного примера дизъюнкта в

S .

О

п

р

е

д

е

л

е

н

и

е

.

. Говорит, что семантическое дерево закрыто, если и только если

каждая ветвь дерева оканчивается опровергающим узлом.

О

п

р

е

д

е

л

е

н

и

е

.

. Узел

N закрытого семантического дерева называется выводящим

узлом, если все непосредственно следующие за

N узлы являются опровергающими.

Например: Пусть

{}

PVRQPVRQVPS ⎤⎤⎤⎤= ,,, эрбрановский базис множества S есть

{}

RQPA ,,= . Полное семантическое дерево для S имеет вид а) (предыдущий пример),

а закрытое семантическое дерево для

S имеет вид

P

О P⎤

О О

Q Q⎤

О О

R

R⎤

О О

Рис. 7

Математическая Логика и Теория Алгоритмов стр. 35 из 64

Лекция 7

Доказательство теорем в исчислении предикатов.

Теорема Эрбрана.

Перейдем к рассмотрению теорем Эрбрана, которая послужила основой для по-

строения машинных алгоритмов и программ доказательства теоремы. Существуют

два варианта теоремы Эрбрана.

Т

е

о

р

е

м

а

Э

р

б

р

а

н

а

(

в

а

р

и

а

н

т

1

)

.

Множество дизъюнктов S невыполнимо тогда

и только тогда, когда любому полному семантическому дереву множества

S существу-

ет конечное закрытое дерево.

Доказательство.

Необходимость.

Пусть S невыполнимо и

T

- полное семантическое дерево для

S . Для каждой ветви

B

дерева

T

пусть

B

I

- множество всех литер, приписанных реб-

рам ветви

B

. Тогда

B

I есть интерпретация для

S

. Так как

S

невыполнимо, то

B

I долж-

на опровергать основной пример

'

C некоторого дизъюнкта

C

в

S

(т.е.

'

C должен иметь

значение 0). Однако, т.к.

'

C конечно, то на

B

должен существовать опровергающий

узел

B

N

, лежащий на конечном расстоянии (конечное число ребер в ветви

B

) от

корневого узла дерева

T

. Поскольку каждая ветвь дерева имеет опровергающий

узел, то существует закрытое семантическое дерево

'

T

для S . Далее, т.к. из каждого

узла

'

T

выходит только конечное число ребер, то число ветвей, образованных в де-

реве

'

T

конечно, а следовательно конечно и число вершин (узлов)

'

T

, т.е. полному

семантическому дереву

T

для S соответствует конечное закрытое семантическое де-

рево

'

T

.

Достаточность

. Пусть теперь для каждого полного семантического дерева

T

для

S существует конечное закрытое семантическое дерево

'

T

. Тогда каждая ветвь дере-

ва

T

содержит опровергающий узел. Это означает, что каждая интерпретация опро-

вергает

S . Следовательно, согласно теореме о невыполнимости множества дизъюнк-

тов (см. стр 57), множество дизъюнктов

S

невыполнимо. Теорема доказана.

Приведем теперь второй вариант теоремы Эрбрана

Т

е

о

р

е

м

а

Э

р

б

р

а

н

а

(

в

а

р

и

а

н

т

2

)

.

Множество дизъюнкторов S невыполнимо то-

гда и только тогда, когда существует конечное невыполнимое множество

'

S основных

примеров дизъюнктов из

S .

Доказательство.

Необходимость.

Пусть

S

невыполнимо и

T

- полное семантическое дерево для

S

. Тогда по теореме Эрбрана (вариант 1) существует конечное закрытое семантиче-

ское дерево

'

T

, соответствующее

T

. Пусть

'

S - множество всех основных примеров

дизъюнктов, которые опровергаются во всех опровергающих узлах

'

T

. Тогда

'

S ко-

нечно, т.к. в

'

T

конечное число опровергающих узлов. Так как

'

S ложно в каждой ин-

терпретации для

'

S , то

'

S - невыполнимо.

Достаточность

. Предположим существует конечное невыполнимое множество

'

S

основных примеров дизъюнктов из S . Так как каждая интерпретация

I

для S со-

держит интерпретацию

'

I

множества

'

S и

'

I

опровергает

'

S , то

I

должна также опро-

вергать

'

S . Однако

'

S опровергается в каждой интерпретации

'

I

, поэтому

'

S опровер-

гается в каждой интерпретации

I

. Следовательно,

'

S

опровергается в каждой интер-

претации

I

множества S . А так как

'

S есть множество основных примеров дизъюнктов

из

S и

'

S опровергается в каждой интерпретации

I

множества S , то множества дизъ-

юнктов

S опровергается в каждой интерпретации для S , а потому невыполнимо. Тео-

рема доказана.

Математическая Логика и Теория Алгоритмов стр. 36 из 64

Например:

Пусть

{}

))((),( afPxPS ⎤ . Эрбрановский универсум этого множества

{}

...)),((),(, affafaH = , эрбрановский базис

{

}

)),...((()),((, affPafPaA

=

, полное семан-

тическое дерево имеет вид

)(aP О

)(aP⎤

О О

))(( afP ))(( afP⎤ ))(( afP⎤

))(( afP

О О О О

)))((( affP⎤ )))((( affP

О О

Это дерево имеет конечное замкнутое (закрытое) семантическое дерево вида

)(aP О

)(aP⎤

О О

))(( afP ))(( afP⎤

О О

Поэтому множество

S невыполнимо, а в качестве невыполнимого множества

'

S основных примеров дизъюнктов множества S можно указать

{}

))(()),((),( afPafPaP ⎤⎤ . Легко видеть, что в качестве множества

'

S можно взять также

{}

))(()),(( afPafP ⎤ , конъюнкция которых ложна в любой интерпретации.

Методы доказательства теорем.

Как мы уже отмечали ранее теорема о дедукции в исчислении высказываний

позволяет свести задачу о выводимости некоторой формулы из множества формул

(т.е. задачу доказательства теорем) к задаче о доказательстве общезначимости или

противоречивости пропозиционных форм. Этот же факт как было

показано выше ис-

пользуется и при доказательстве теорем в исчислении предикатов первого порядка.

В соответствии с теоремой Эрбрана для доказательства невыполнимости мно-

жества

S

дизъюнктов достаточно найти конечное невыполнимое множество

'

S основ-

ных примеров дизъюнктов из

S . Так как, основные примеры по определению не за-

висят от переменных, то доказать противоречивость некоторого множества

'

S

основ-

ных примеров можно как и в исчислении высказываний, т.е. путем приведения ис-

ходной конъюнкции дизъюнкций к дизъюнктивной нормальной форме (дизъюнкция

конъюнкций). Однако при использовании такого метода доказательства теорем на-

блюдается экспоненциональный рост числа конъюнкций в неблагоприятных ситуаци-

ях.

Математическая Логика и Теория Алгоритмов стр. 37 из 64

Дэвис М. и Патнем Х. Превратили другой, более эффективный метод проверки

невыполнимости множества дизъюнктов (т.е. по сути дела метод доказательства тео-

рем). Суть этого способа заключается в использовании следующих четырех правил:

1. Правило тавтологии.

Вычеркнем все тавтологичные основные дизъ-

юнкты (т.е. дизъюнкты, которые не зависят от переменных) из

S

, то-

гда оставшееся множество невыполнимо в том и только в том случае,

когда и

S невыполнимо.

2. Правило однолитерных дизъюнктов.

Если существует единичный ос-

новной дизъюнкт

L в S , то

'

S получается из S вычеркиванием тех ос-

новных дизъюнктов в

S , которые содержат

L

. Если

'

S пусто, то S вы-

полнимо, в противном случае построим множество

*

S

, выбрасывая из

'

S вхождения L⎤ . Тогда

*

S невыполнимо в том и только в том случае

когда и

S невыполнимо. Заметим, что если L⎤ единичный основной

дизъюнкт, то при вычеркивании

L⎤

он превратится в 0.

3. Правило чистых литер.

Назовем литеру L в основном дизъюнкте из

S чистой в S тогда и только тогда, когда литера L⎤ не находится ни в

одном основном дизъюнкте из

S . Если литера L чистая в S , то вы-

черкнем все основные дизъюнкты, содержащие

L . Оставшееся мно-

жество невыполнимо тогда и только тогда, когда и

S невыполнимо.

4. Правило расщепления.

Если множество S можно представить в виде

,&)(&...&)(&)(&...&)(

11

RLVBLVBVLAVLA

nm

⎤⎤ где RBA

ii

,

- свободны от L

и

L⎤ , то получим множества расщепления

RBBBS

RAAAS

n

m

&&...&&

212

211

=

Множество

S невыполнимо тогда и только тогда, когда )(

21

VSS невыполнимо т.е. и

1

S и

2

S - невыполнимы.

Обоснуем возможность применения этих правил. Для этого необходимо доказать,

что преобразованное множество дизъюнктов невыполнимо тогда и только тогда, когда

невыполнимо исходное множество дизъюнктов.

Правило тавтологии применимо т.к. тавтологии выполняются в любой интерпре-

тации, а поэтому

'

S

невыполнимо тогда и только тогда, когда S невыполнимо.

Рассмотрим правило однолитерных дизъюнктов

. Если

'

S пустое множество, то все

дизъюнкты из

S содержат L . Следовательно, всякая интерпретация, содержащая L ,

может удовлетворять

S . Поэтому S выполнимо. Покажем теперь, что

*

S невыполнимо

тогда и только тогда, когда

S

невыполнимо. Предположим, что

*

S невыполнимо. Если

S выполнимо, то существует модель

M

для S , содержащая L . Для

*

S модель

M

долж-

на удовлетворять всем дизъюнктам, которые не содержат

L . Далее т.к.

M

опроверга-

ет

L⎤ , модели

M

должны удовлетворять все дизъюнкты, которые первоначально со-

держали

L⎤ . Следовательно модель

M

должна быть и моделью для

*

S

, что противо-

речит предложению о невыполнимости

*

S . Поэтому S должно быть невыполнимо.

Предположим теперь, что

S невыполнимо. Если

*

S выполнимо, то существует мо-

дель

*

M

для

*

S

. Таким образом, всякая интерпретация S , содержащая

*

M

и L , долж-

на быть моделью для

S

. Это противоречит предположению, что

S

не имеет модели.

Поэтому

*

S должно быть невыполнимо. Следовательно

*

S невыполнимо тогда и только

тогда, когда

S невыполнимо.

Дадим обоснование правила чистых литер. Предположим, что

'

S невыполнимо.

Тогда

S

должно быть невыполнимо, так как

'

S есть подмножество

S

. Наоборот, пред-

положим теперь, что

S невыполнимо. Если

'

S

выполнимо, то существует модель

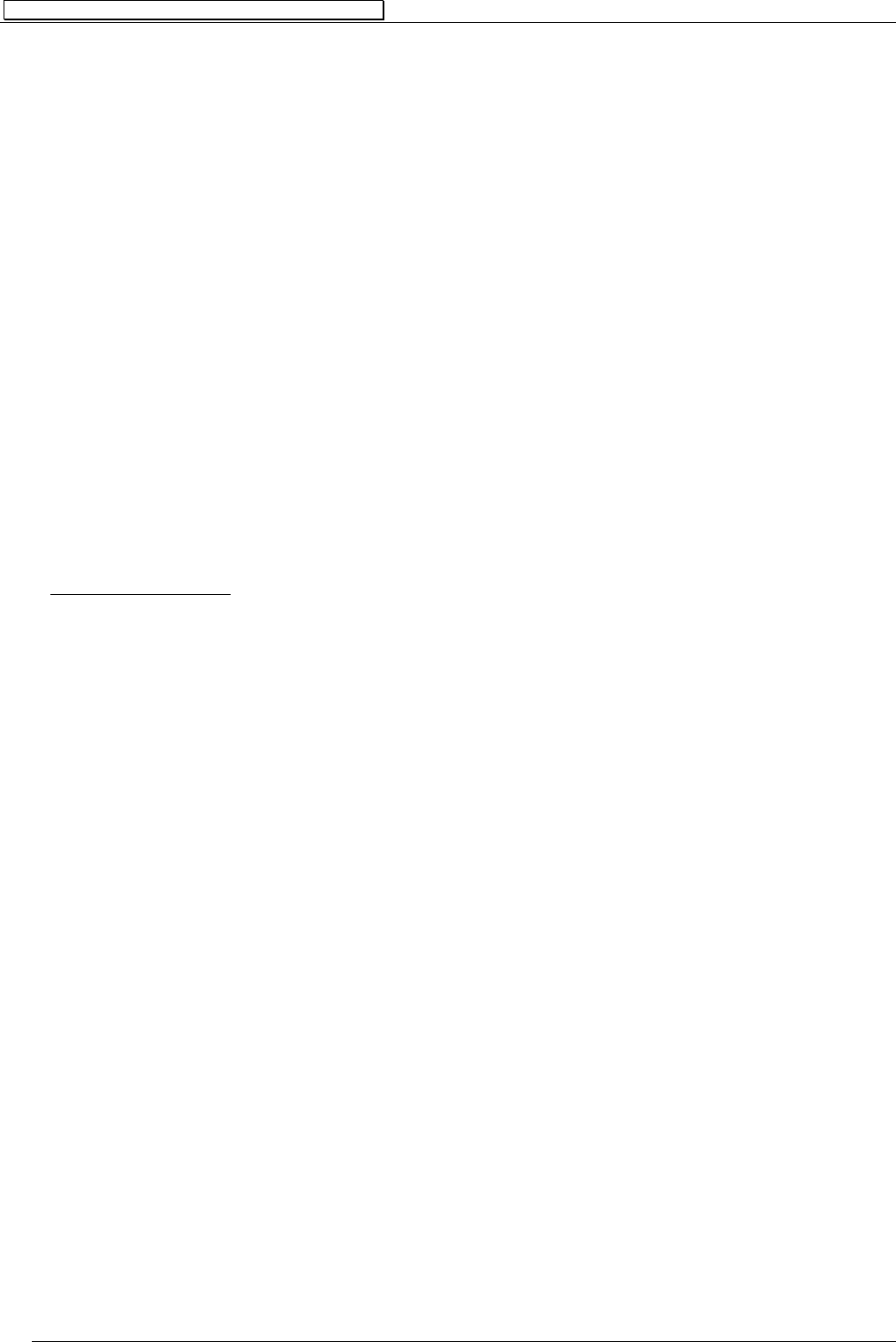
Математическая Логика и Теория Алгоритмов стр. 38 из 64

M

для

'

S . При этом ни L ни L⎤ не находятся ни в

'

S ни в

M

. Таким образом, всякая

интерпретация для

S , которая содержит

M

и L есть модель для S . Это противоречит

тому, что

S не имеет модели, т.е. предположению, что S невыполнимо. Поэтому

'

S должно быть невыполнимо. Следовательно

'

S невыполнимо тогда и только тогда,

когда

S невыполнимо.

Приведем обоснование правила расщепления. Предположим, что

S невыполнимо.

Если

)(

21

VSS

выполнимо, то или

1

S

или

2

S

имеют модель.

)(

21

SS

имеет модель

M

, то

всякая интерпретация для

S , содержащая

)( LL ⎤

есть модель для S , что противоре-

чит предложению о том, что

S не имеет модели (т.е. невыполнимо). Следовательно

)(

21

SS

невыполнимо.

Пусть теперь

)(

21

SS невыполнимо, если

S

выполнимо, то

S

имеет модель

M

. Если

M

содержит )(LL⎤ , то

M

является моделью для

)(

21

SS

. Это противоречит предполо-

жения о том, что

)(

21

SS невыполнимо. Следовательно

S

невыполнимо тогда и только

тогда, когда

21

VSS невыполнимо.

Рассмотренный метод доказательства может быть применен к любой формуле по-

сле ее приведения к конъюнктивной нормальной форме (конъюнкция дизъюнкций).

Общим недостатком методов доказательства невыполнимости множества дизъ-

юнктов, основанных на теореме Эрбрана, является необходимость порождения ос-

новных примеров дизъюнктов, число которых как правило, растет экспоненционально

с увеличением номера

i

уровня множества

i

H констант,

∞

=

...,2,1i .

Метод резолюций

свободен от этого недостатка и не требует порождения множе-

ства основных примеров дизъюнктов. Этот метод предложен Дж.Робинсоном в 1965

году. Основная идея этого метода состоит в том, чтобы проверить содержит ли

S

пус-

той дизъюнкт 0. Если

S

содержит 0, то

S

невыполнимо, в противном случае проверя-

ется, может ли быть получен 0 из

S .

Рассмотрим сначала метод резолюций для доказательства теорем в исчислении

высказываний.

Сформулируем правило резолюций являющееся обобщением правила однолитер-

ных дизъюнктов.

Правило резолюций. Для любых двух дизъюнктов

1

С и

2

С , если существует лите-

ра

1

L в

1

C , контрарная литере

2

L в

2

C , то вычеркнув

1

L и

2

L из

1

C и

2

C соответственно,

построим дизъюнкцию оставшихся дизъюнктов. Построенный таким образом дизъюнкт

есть резольвента

1

С и

2

С .

Рассмотрим пример.

Пусть

PVRС =

1

PVQC =⎤ . Дизъюнкт

1

C имеет литеру

P

, контрарную литере

P⎤

из

2

C . Значит, в соответствии с правилом резолюций из

1

C и

2

C получаем резольвенту

RVQ .

Имеет место следующая теорема.

Т

е

о

р

е

м

а

.

. Пусть даны два дизъюнкта

1

C

и

2

C

. Тогда резольвента C дизъюнктов

1

C и

2

C есть логическое следствие

1

C и

2

C .

Если имеется два единичных дизъюнкта и существует их резольвента, то эта ре-

зольвента есть пустой дизъюнкт 0. Существенным является тот факт, что для невы-

полнимого множества дизъюнктов применениями правила резолюций можно породить

0.

Пусть

S - множество дизъюнктов. Резолютивный вывод C из S есть такая конеч-

ная последовательность

k

CC ...,,

1

дизъюнктов, что каждый

i

C или принадлежит S или

является резольвентом дизъюнктов, предшествующих

i

C и тогда

k

C есть C . Вывод 0

из

S называется опровержением (или доказательством невыполнимости) S .

Математическая Логика и Теория Алгоритмов стр. 39 из 64

Таким образом, правило резолюций есть правило вывода. Это правило является

обобщением правила

MP

и имеет вид

B

AVBA

⎤,

. Говорят, что дизъюнкт C может быть

выведен или получен из

S , если существует вывод C из S . Вывод может быть пред-

ставлен деревом вывода

, вершина которого – дизъюнкты резолютивного вывода и в

любую вершину заходят только ребра, исходящие из дизъюнктов – посылок правила

резолюций; в дизъюнкты из множества

S ребра не заходят.

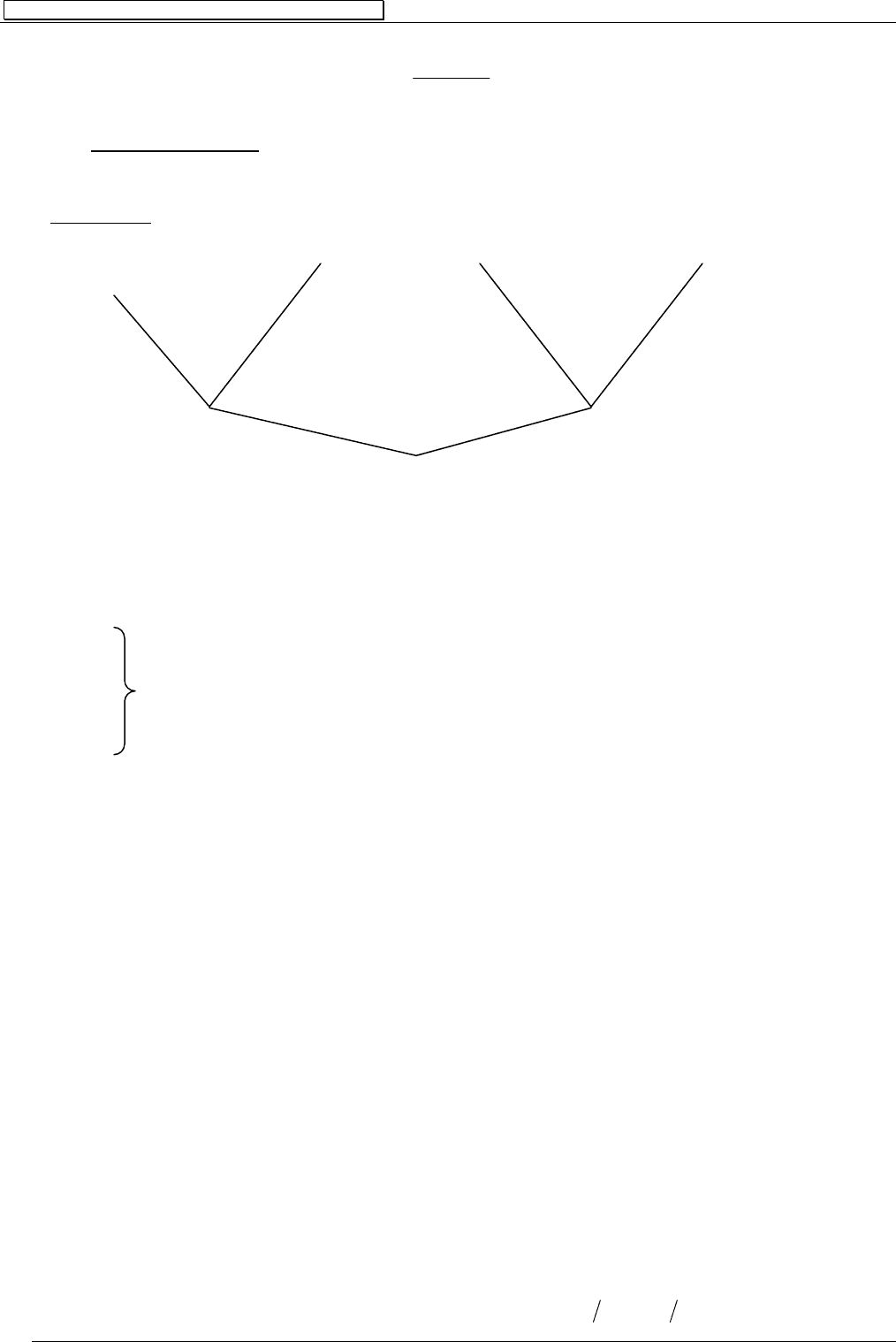
Например

дерево вида

О

PVQ О PVQ⎤ О QPV ⎤

О

QPV ⎤⎤

О

Q О Q⎤

О

0

соответствует следующему выводу

1.

PVQ

2.

PVQ⎤ S

3.

QPV ⎤

4.

QPV ⎤⎤

5.

Q из 1 и 2

6.

Q⎤ из 3 и 4

7. 0 из 5 и 6

В случае исчисления предикатов применение метода резолюций осложняется за-

висимостью дизьюнктов от переменных.

Например рассмотрим дизъюнкты:

)())((:

)()(:

2

xVRxfPC

xVQxPС

⎤

здесь не существует никакой литеры в

1

C , контрарной какой-нибудь литеры в

2

C . Однако, если представить

)(af

вместо

X

в

1

C и а вместо

X

в

2

C то получим

))(())((:

'

1

afVQafPC

)())((:

'

2

aVRafPС ⎤

и из

'

1

C и

'

2

C можно уже получить резольвенту

)())((:

'

3

aVRafQC .

Ясно, что получение резольвент из дизъюнктов требует выполнения операций

подстановки.

Подстановкой назовем конечное множество вида:

},,{

11 nn

htht K ,

Математическая Логика и Теория Алгоритмов стр. 40 из 64

Где

i

h - переменная,

i

t - терм отличный от

i

h ; все

i

h различны ),,1( ni K= .

Если термы

n

tt ,,

1

K не содержат переменных, то подстановка называется основ-

ной. Подстановка, не содержащая элементов называется пустой и обозначается

ξ

.

Если

E

- выражение и

⎭

⎬

⎫

⎩

⎨

⎧

=Θ

n

t

γγ

...

1

- подстановка, то результат операции под-

становки

),...,(

1 n

tt вместо переменных

n

γ

...,

1

в выражение

E

будем обозначать

Θ

E

, при

этом

ΘE называют примером

E

.

Определение. Пусть

⎭

⎬

⎫

⎩

⎨

⎧

=Θ

n

x

t

x

t

,...,

1

и

⎭

⎬

⎫

⎩

⎨

⎧

=

m

y

u

y

u

,...,

1

μ

две подстановки. Тогда

композиция

Θ и

μ

есть подстановка, обозначаемая

ομ

Θ

, которая получается из мно-

жества

⎭

⎬

⎫

⎩

⎨

⎧

m

n

y

u

y

u

x

t

x

t

,...,,...,

1

μμ

вычеркиванием всех элементов

j

x

t

μ

, для которых

jj

xt =

μ

(т.е. исключается подстановка переменной вместо самой себя) и всех элемен-

тов

i

y

u

таких, что

{

}

nj

xxy ,,

1

K∈ (исключается неоднозначность подстановки).

Например:

{}(){}

yzxyfxtxt ,,

2211

==Θ

{

} {}

zyybxayuyuyu ,,,,

332211

=

μ

Тогда

(

)

{

}

z

y

b

x

a

y

x

bf

y

u

y

u

y

u

x

t

x

t

,,,,,,,,

3

2

1

2

1

=

⎭

⎬

⎫

⎩

⎨

⎧

μμ

Так как

22

xt =

μ

, то

2

x

t

μ

(т.е.

y

) должно быть вычеркнуто из множества. Так

как

1

y и

2

y содержатся среди

{}

21

, xx , то

1

y

u

и

2

y

u

должны быть вычеркнуты. В ре-

зультате получаем

()

{

}

z

y

x

bf

,=Θ

μ

o .

Применение метода резолюций требует нахождение подстановки, которая может

сделать несколько выражений тождественными (т.е. унифицировать или склеить вы-

ражения).

Подстановка

Θ

называется унификатором для множества выражений

{}

n

EE ,,

1

K ,

тогда и только тогда, когда

Θ

n

EEE ,,,

21

K совпадают между собой. Говорят, что

множество

{}

n

EE ,,

1

K унифицируемо, если для него существует унификатор.

Унификатор

σ

для множества выражений

{

}

n

EE ,,

1

K называется наиболее общим

унификатором, если и только если для каждого унификатора

Θ

для этого множества

существует такая подстановка

μ

, что

μ

σ

o

=

Θ

.

Приведем алгоритм нахождения наиболее общего унификатора (НОУ) для конеч-

ного унифицируемого множества выражений. Если множество не унифицируемо, то

алгоритм будет этот факт выявлять.

Суть алгоритма заключается в просмотре выражений слева направо, выявлении

первого различия (рассогласования), выделении соответствующих выражений, начи-

нающихся с соответствующих позиций, после чего делается попытка исключения рас-

согласования

и т.д.

Множество рассогласований непустого множества выражений W получается вы-

явлением первой (слева) позиции, на которой не для всех выражений из W стоит

один и тот же символ и затем выписываем из каждого выражения в W подвыражения,

которое начинается с символа, занимающего эту позицию. Множество этих выраже-

ний и будет множеством рассогласований W.

Например

, если

()()

(

)

(

)

(

)

(

)

(

){}

xKhgxPaxPzyfxPW ,,,,,,

=

то множество рассогласова-

ний W есть

() ()()(){}

xKhgazyf ,,,

Галуев Г.А. Математическая логика и теория алгоритмов

Подождите немного. Документ загружается.