Галуев Г.А. Математическая логика и теория алгоритмов

Подождите немного. Документ загружается.

Математическая Логика и Теория Алгоритмов стр. 11 из 64

Под словом «эффективно» подразумевается то, что существует некоторая предо-

пределённая последовательность действий (т.е. алгоритм, процедура), позволяющая

за конечное число шагов ответить на требуемый вопрос положительно или отрица-

тельно.

Выводом в теории Т называется всякая конечная последовательность А

,…,А

формул такая, что для любого i формула А

есть либо аксиома теории Т, либо непо-

средственное следствие каких-либо предыдущих формул по одному из правил выво-

да.

Формула А теории Т называется теоремой этой теории, если существует вывод в

Т, в котором последней формулой является А. Такой вывод называется доказательст-

вом (выводом) формулы А.

Следует отметить, что понятие

теоремы не обязательно эффективно, т.е. может и

не существовать эффективной процедуры, позволяющей определить по данной фор-

муле, существует ли её вывод в теории Т. Теория, для которой такой алгоритм суще-

ствует называется разрешимой, в противном случае – неразрешимой.

Формула А является следствием множества формул Г в теории Т тогда и только

тогда, когда существует такая конечная последовательность формул А

,…,А

, что А

есть А и для каждого i A

есть либо аксиома, либо элемент Г, либо непосредственное

следствие некоторых предыдущих формул по одному из правил вывода. Такая после-

довательность называется выводом А из Г. Члены множества формул Г называются

гипотезами или посылками вывода. Утверждение типа «А есть следствие Г» обозна-

чают Г├А (можно читать «Г даёт А»). Для

указания того, что А есть следствие Г имен-

но в теории Т пользуются обозначением Г├

А. Для конечного множества Г={В

,…,В

(где В

∈

Г элементы множества Г) вместо {В

,…,В

}├

А обычно пишут В

,…,В

├

А.

Если Г пустое множество ∅ (т.е. множество не содержащее ни одного элемента),

то Г├А тогда и только тогда, когда А является теоремой (т.е. аксиомой или формулой

выводимой из аксиомы). Вместо ∅├А пишут ├А (т.е. А теорема).

Очевидными являются следующие свойства понятия выводимости:

1. Если

Г Δ⊆ (т.е. «Г подмножество

», «Г включается в

») и Г├А, то Δ├А. Т.е.

если А выводимо из Г, то оно выводимым будет если к Г добавить новые

посылки.

2. Г├А тогда и только тогда, когда в Г существует конечное подмножество Δ, для

которого Δ├А. Достаточность условия вытекает из предыдущего свойства.

Необходимость вытекает из

того, что каждый вывод А из Г использует

лишь конечное число посылок из Г.

3. Если Δ├А и Г├В для любого В из множества Δ, то Г├А, т.е. если А выводима из

Δ и каждая формула из Δ выводима из Г, то А выводима из Г.

Рассмотрим

теперь формальную аксиоматическую теорию L для классического

исчисления высказываний (Д. Гильберт, П. Бернайс, С. Клини):

I. Символами L являются ⎤, →, (,) и буквы А с целыми положительными

числами в качестве индексов: А

, А

,… Символы ⎤ , → называют при-

митивными связками, а буквы А

, А

,… - пропозиционными буквами;

II. а) Все пропозиционные буквы А

б) Если А и В формулы, то (⎤А) и (А→В) – тоже формулы

в) Никаких других формул, кроме определённых согласно а) и б)

нет.

III. Каковы бы ни были формулы А, В, С теории L, следующие формулы

есть аксиомы L:

(АК1) А→(В→А)

(АК2) (А→(В→С))→((А

→В)→(А→С))

(АК3) (⎤В→⎤А)→((⎤В→А)→В)

IV. Единственное используемое правило вывода: В есть непосредствен-

ное следствие А и А→В. Это записывают в виде:

А и А→В – посылки А, А→В

Это правило называют modus В – за-

ключение В ponens (МР) или правило отделения

Математическая Логика и Теория Алгоритмов стр. 12 из 64

Отметим, что выражения АК1, АК2, АК3 представляют собой не конкретные ак-

сиомы, а схемы аксиом, с помощью которых можно получить бесчисленное множество

аксиом, подставляя в них вместо А, В, С конкретные формулы. Например, если А есть

→А

, В есть ⎤А

, то из АК1 получим конкретную аксиому:

→А

→(⎤А

→(А

→А

)).

Отметим также и то, что знаки ⎤ , → в формальной теории выступают просто как

формальные символы, а не как рассматриваемые ранее операции «отрицания», и

«импликации». Учитывая сказанное можно с помощью определений ввести и другие

связки:

А&В есть ⎤(А→⎤В)

А∨В есть ⎤А→В

А↔ есть (А

→В)&(В→А)

Здесь &, ∨, ↔ также трактуются как абстрактные знаки.

Лекция №3

Рассмотрим примеры доказательства теорем в теории L.

Докажем, что для любой формулы А справедливо ├

А→А(***).

Для доказательства этого утверждения построим вывод формулы А→А в теории L.

1. (А→((А→А)→А))→((А→(А→А))→(А→А)) (получается подстановкой в схему

аксиом АК2 А→А вместо В и А вместо С)

2. А→((А→А)→А) (получается подстановкой в АК

1 А вместо В)

3. (А→(А→А))→(А→А) (получается из 2 и 1 по правилу МР)

4. А→(А→А) (получается подстановкой в АК! А вместо В)

5. А→А (получается из 4,3 по правилу МР)

Таким образом ├

А→А доказано

Докажем, что для любой формулы А справедливо ├

(⎤А→А)→А.

1. (⎤А→⎤А)→((⎤А→А)→А) (получаем подстановкой А в АК3 вместо В)

2. ⎤А→⎤А (получаем подстановкой ⎤А в (***) вместо А)

3. (⎤А→А)→А (получаем из 2, 1 по правилу МР)

Таким образом ├

(⎤А→А)→А доказано.

Докажем, что для любых А, В, С справедливо А→В, В→С├

А→С (****).

1. (А→(В→С))→((А→В)→(А→С)) (схема АК2)

2. (В→С)→((А→(В→С)) (получаем из АК1 подстановкой В→С вместо А и А

вместо В)

3. (В→С) (гипотеза)

4. А→(В→С) (по правилу МР из 3 и 2)

5. (

А→В)→(А→С) (по правилу МР из 4 и 1)

6. (А→В) (гипотеза)

7. А→С (по правилу МР из 6 и 5)

Таким образом (****) доказано.

Важное значение в исчислении высказываний имеет теорема о дедукции. Эта

теорема является теоретическим обоснованием используемого в математических рас-

суждениях приёма: доказывается, что В верно в

предположении о верности некоторо-

го утверждения А, после чего заключается, что верно утверждение «Если А, то В».

(

)

. Если Г, А├В, то Г├А

→

В, где: Г – множество формул; А,

В – формулы.

Теорема (о дедукции) впервые явно сформулирована у Эрбрана в 1930г и имела

следующий вид: а) Если А├В, то ├А→В

б) Если А

,…,А

m-1

,А

├В, то A

,…,A

m-1

├A

→В

В нашей формулировке теорема учитывает оба случая а) и б) из теоремы Эрбра-

на.

Математическая Логика и Теория Алгоритмов стр. 13 из 64

Доказательство.

Пусть В

,…,В

есть вывод из Г ∪ {А} (множество содержащее элементы из Г и

формулу А), где В

есть В.

Индукцией по i докажем, что Г├А→В

, i=1,…,n.

Рассмотрим случай i=1. Формула В

должна быть либо элементом Г, либо аксио-

мой теории L, либо совпадать с А. По схеме аксиом АК1 формула В

→(А→В

) есть ак-

сиома. Поэтому в первых двух случаях Г├А→В

по правилу МР

, В

→(А→В

)

А→В

В третьем случае, когда В

есть А, в соответствии с (***) (т.е. ├А→А) имеем

├А→В

и поэтому Г├А→В

. Тем самым базис индукции при i=1 доказан.

Делаем теперь индуктивное предположение: Г├А→В

для любого к<i и попыта-

емся доказать, что тогда и Г├А→В

. Для В

имеем следующие 4 возможности: 1. В

есть

аксиома.

2. В

∈Г. 3. Вi есть А. 4. В

следует по правилу МР из некоторых В

и В

(j<i, m<i) и В

имеет вид В

→B

В первых трёх случаях Г├А→В

доказывается также как и для случая i=1. В по-

следнем четвёртом случае применим индуктивное предположение, согласно которому

Г├А→В

и Г├А→В

, т.е. Г├А→(В

→B

). Подставляя в схему аксиом АК2 В

вместо В и В

вместо С имеем: ├(А→(В

→B

))→((A→B

)→(A→B

)). Следовательно, по правилу МР по-

лучаем из второго индуктивного предположения (Г├А→В

или Г├А→В

→B

т.к. В

есть

→B

Г├(А→В

)→(A→B

), откуда из первого индуктивного предположения (А→В

) по

правилу МР имеем Г├А→В

Таким образом доказано, что для любого i справедливо Г├А→В

, откуда при i=n

получаем требуемое утверждение.

Следствие. Если А├В, то ├А→В.

Теорема о дедукции позволяет облегчить процедуры доказательств. Например,

докажем для любых А, В, С справедливость (****) А→В, В→С├

А→С.

1. А (гипотеза)

2. А→В (гипотеза)

3. В (по правилам МР из 1 и 2)

4. В→С (гипотеза)

5. С (по правилам МР из 3 и 4, когда А есть В и В есть С).

Следовательно А→В, В→С, А├С, откуда по теореме о дедукции А→В, В→С

├А→С.

Приведём ещё один пример. Докажем, что А→(В→С), В├А→С (*****)

1. А (гипотеза

2. А→(В→С) (гипотеза)

3. В→С (по правилу МР из 1 и 2 где А есть А и В есть В→С)

4. В (гипотеза)

5. С (по правилу МР из 4 и 3

где А есть В и В есть С)

Следовательно А→(В→С), А, В├С, откуда по теореме о дедукции А→(В→С),

В├А→С.

Докажем два важных для исчисления высказываний утверждения.

Утверждение 1.

Если Г, А├В и Г, А├⎤В, то Г├⎤А. Это утверждение называют «Reductio ad

absurdum» -

приведение к абсурду.

Доказательство.

1. Г├А→В (по теореме о дедукции)

2. Г├А→⎤В (по теореме о дедукции)

3. (⎤⎤А→⎤⎤В)→((⎤⎤А→⎤В)→⎤А) (из схемы АК3 с ⎤А вместо В и ⎤В вместо А)

Теперь, если доказать выводимость ⎤⎤А→⎤⎤В и ⎤⎤А→⎤В

из А→В и А→⎤В, то восполь-

зовавшись дважды правилом МР, из 3 можно вывести ⎤А. Покажем, что А→В├⎤⎤А→⎤⎤В.

Для этого сначала убедимся, что ⎤⎤А→А.

(1)

Математическая Логика и Теория Алгоритмов стр. 14 из 64

4. (⎤А→⎤⎤А)→((⎤А→⎤А)→А) (по схеме АК3 с А вместо В, и ⎤А вместо А)

5. ⎤А→⎤А (из (***), т.е. ├

А→А с ⎤А вместо А)

6. (⎤А→⎤⎤А)→А (из 4,5 и (*****), т.е. А→(В→С), В├А→С с (⎤А→⎤⎤А) вместо А,

(⎤А→⎤А) вместо В, и А вместо С)

7. ⎤⎤А→(⎤А→⎤⎤А) (по схеме АК1 с ⎤⎤А вместо А и

⎤А вместо В)

8. ⎤⎤А→А (из 6,7 и (****), т.е. А→В, В→С├А→С с ⎤⎤А вместо А, (⎤А→⎤⎤А) вместо В

и А вместо С)

9. ⎤⎤А (гипотеза)

10.А (по правилу МР из 9 и 8)

Таким образом доказано, что ⎤⎤А→А. Теперь нетрудно доказать, что

А→В├⎤⎤А→⎤⎤В.

11.А→В (гипотеза)

12.В (по правилу МР из 10,11)

Если В├⎤⎤В, то отсюда будет вытекать, что ⎤⎤А, А→В├⎤⎤В.

13.(⎤⎤⎤В→⎤В)→((⎤⎤⎤В→В)→⎤⎤В) (по схеме АК3 с ⎤⎤В вместо В, и В вместо А)

14.⎤⎤⎤В→⎤В (из

(1) с ⎤В вместо А)

15.(⎤⎤⎤В→В)→⎤⎤В (по правилу МР из 14,13)

16.В→(⎤⎤⎤В→В) (из схемы АК1 с В вместо А и ⎤⎤⎤В вместо В)

17.В→⎤⎤В (из 16,15 и (****), т.е. А→В, В→С├А→С с В вместо А, ⎤⎤⎤В вместо В и

⎤⎤В

вместо С)

18.В (гипотеза)

19.⎤⎤В (по правилу МР из 18,17)

Таким образом доказано, что В├⎤⎤В (2)

Следовательно, ⎤⎤А, А→В├⎤⎤В, откуда по теореме о дедукции следует:

20.А→В├⎤⎤А→⎤⎤В

21.(⎤⎤А→⎤В)→⎤А (из 20 и 3 по правилу МР)

Докажем теперь, что А→⎤В├⎤⎤

А→⎤В.

22.⎤⎤А, А→⎤В├⎤В (из (1) по правилу МР)

23.А→⎤В├⎤⎤А→⎤В (из 22 по теореме о дедукции)

24.⎤А (из 23 и 21 по правилу МР)

Таким образом доказано, что Г├⎤А или Г, А├В и Г, А├⎤В, что и требовалось дока-

зать.

Рассмотрим ещё

одно утверждение, показывающее, что из противоречия А и ⎤А

выводима любая формула В.

Утверждение 2.

Для любых формул А и В справедливо: А, ⎤А├В

(3)

Доказательство.

1. А, ⎤А, ⎤В├А приведение к абсурду в

2. А, ⎤А, ⎤В├⎤А соответствии с утверждением 1

3. А, ⎤А├⎤⎤В (из 1 и 2 в соответствии с утверждением ├

А→А (***))

4. А, ⎤А├В (из 3 и (1) (⎤⎤А├А) с В вместо А)

Непротиворечивость и полнота исчисления высказываний.

Непротиворечивость. Исчисление высказываний (как и вообще любая формаль-

ная система, имеющая символ ⎤ - отрицания) называется непротиворечивой системой,

если ни для какой формулы А, формулы А и ⎤А не являются обе

доказуемыми в этой

системе, и противоречивой в противном случае.

Для исчисления высказываний это определение эквивалентно следующему. Сис-

тема непротиворечива, если в ней имеется некоторая недоказуемая формула; проти-

воречива, если любая формула доказуема.

Действительно, если ├А (А – теорема) и ├⎤А (⎤А – теорема), то в силу доказанно-

го утверждения 2 имеем ├

В и для любой формулы В.

⎭

⎬

⎫

Математическая Логика и Теория Алгоритмов стр. 15 из 64

Доказательство непротиворечивости исчисления высказываний будем искать в

следующих рассуждениях. Предположим, найдено некоторое свойство формул такое,

что

• Аксиомы обладают этим свойством

• При каждом применении правил вывода, если посылки обладают этим

свойством, то и заключение тоже

• Две формулы вида А и ⎤А не могут обе обладать этим свойством.

Тогда

в силу первых двух предположений каждая доказуемая формула обладает

этим свойством и в силу третьего предположения система оказывается непротиворе-

чивой.

Свойство формул, которое можно использовать, вытекает из логической интер-

претации исчисления высказываний (в рамках упоминавшейся выше теории моде-

лей), а именно: доказуемые пропозиционные формулы все оказываются тавтология-

ми, т.е. тождественно

истинными или общезначимыми формулами, которые всегда

принимают значение «истина» (1) при любом распределении значений истинности

составляющих их пропозиционных букв (в этом случае примитивные связки приобре-

тают смысл логических операций &, ∨ →, и т.д.)

. Для того, чтобы пропозиционная форма А

была доказуемой (или выводимой из тождественно истинных формул Г) в исчислении

высказываний необходимо, чтобы она была тождественно истинной, т.е. если ├А, то А

– тавтология.

Справедливость этой теоремы вытекает из

следующих лемм:

Лемма 1.

Пропозиционная формула, являющаяся аксиомой, тождественно истинна.

Для доказательства достаточно построить таблицы истинности для аксиом, полу-

ченных по схемам АК1, АК2, АК3.

Лемма 2.

Если при некотором применении правила вывода МР посылки А и А→В являются

тождественно истинными пропозиционными формами, то и заключение В является

тождественно истинной формулой.

Доказательство

. Рассмотрим таблицу истинности.

А В А А→В

1 1 1 1 1

1 0 1 0 0

0 1 0 1 1

0 0 0 1 0

Табл. 2

Видно, что единственная пара значений истинности А и В, дающая значение 1

обоим посылкам А и А→В это пара А=1, В=1. Эта пара даёт значение 1 и для заклю-

чения В=1.

Следствие. Исчисление высказываний непротиворечиво, т.е. ни для какой фор-

мулы А не имеют место одновременно А и ⎤

А.

Доказательство.

Допустим, что одна из формул А или ⎤А доказуема. Тогда, согласно теореме, эта

формула тавтология. С помощью таблицы истинности убеждаемся, что другая форму-

ла будет тождественно ложной и, следовательно, в силу теоремы недоказуемой.

Полнота.

Для доказательства полноты теории L надо показать, что каждая тавтология яв-

ляется теоремой теории L. Для доказательства этого факта в математической логике

сформулированы и доказаны следующие утверждения.

Если формула А теории L является тавтологией, то

она яв-

ляется теоремой теории L.

Математическая Логика и Теория Алгоритмов стр. 16 из 64

Следствие. Формула А является тавтологией тогда и только тогда, когда А есть

теорема теории L.

Представленные выше результаты доказывают равносильность теории моделей

(метод интуитивных понятий или классическая пропозиционная логика) и теории до-

казательств (аксиоматический метод формальных теорий) на уровне исчисления вы-

сказываний.

В математической логике существуют и другие варианты исчисления высказыва

ний, в основе которых лежат другие наборы примитивных связок, другие аксиомы и

правила вывода. С ними можно ознакомиться в специальной литературе.

Рассмотрим теперь вопрос практического применения математического аппарата

исчисления высказываний в прикладных областях информатики.

Лекция №4.

Применение исчисления высказываний.

Электрические схемы.

Электрическая цепь содержащая только двухпозиционные переключатели (при

одном состоянии переключателя ток проходит через него, при другом – не проходит),

может быть представлена с помощью схемы, на которой возле каждого переключате-

ля пишется пропозиционная буква, истинностное значение которой (1 или 0) соответ-

ствует прохождению или не прохождению тока через переключатель. Тогда условие,

при котором ток

проходит через всю схему, может быть записано в виде пропозици-

онной формулы.

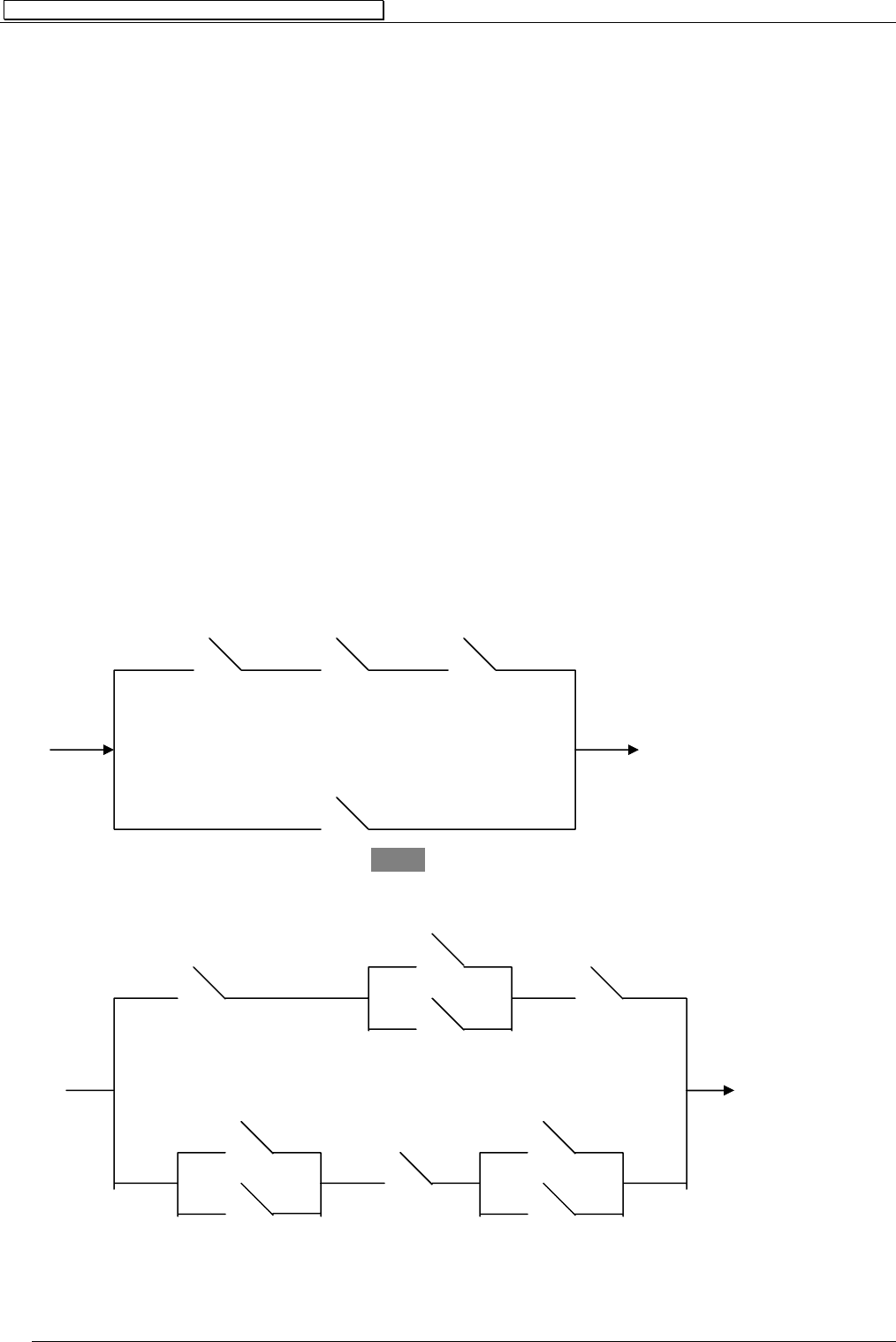
Например, условие, при котором ток проходит через схему на рис.1, может быть

выражено пропозиционной формулой вида

A B C

A&B&C∨D

Рис.1

Пропозиционной форме вида A&(B∨C)&D∨(⎤A∨⎤D)&B&(⎤D∨⎤A) соответствует элек-

трическая цепь вида

A D

⎤A ⎤D

⎤D A

Можно показать, что данная пропозиционная форма с помощью эквивалентных

преобразований аппарата математической логики может быть упрощена. Действи-

тельно,

Математическая Логика и Теория Алгоритмов стр. 17 из 64

A&(B∨C)&D∨(⎤A∨⎤D)&B&(⎤D∨A)↔(A&B∨A&C)&D∨(⎤A∨⎤D)&((B&⎤D)∨(B&A))↔

A&B&D∨A&C&D∨(⎤A∨⎤D)&((B&⎤D)∨(B&A))↔A&B&D∨A&C&D∨((⎤A∨⎤D)&(B&⎤D))∨

∨((⎤A∨⎤

D)&(B&A))↔A&B&D∨A&C&D∨⎤A&B&⎤D∨⎤D&B&⎤D∨⎤A&B&A∨⎤D&B&A↔

A&B&(D∨⎤D)∨A&C&D∨B&⎤D&(1∨⎤A)↔A&(B∨C&D)∨B&⎤D.

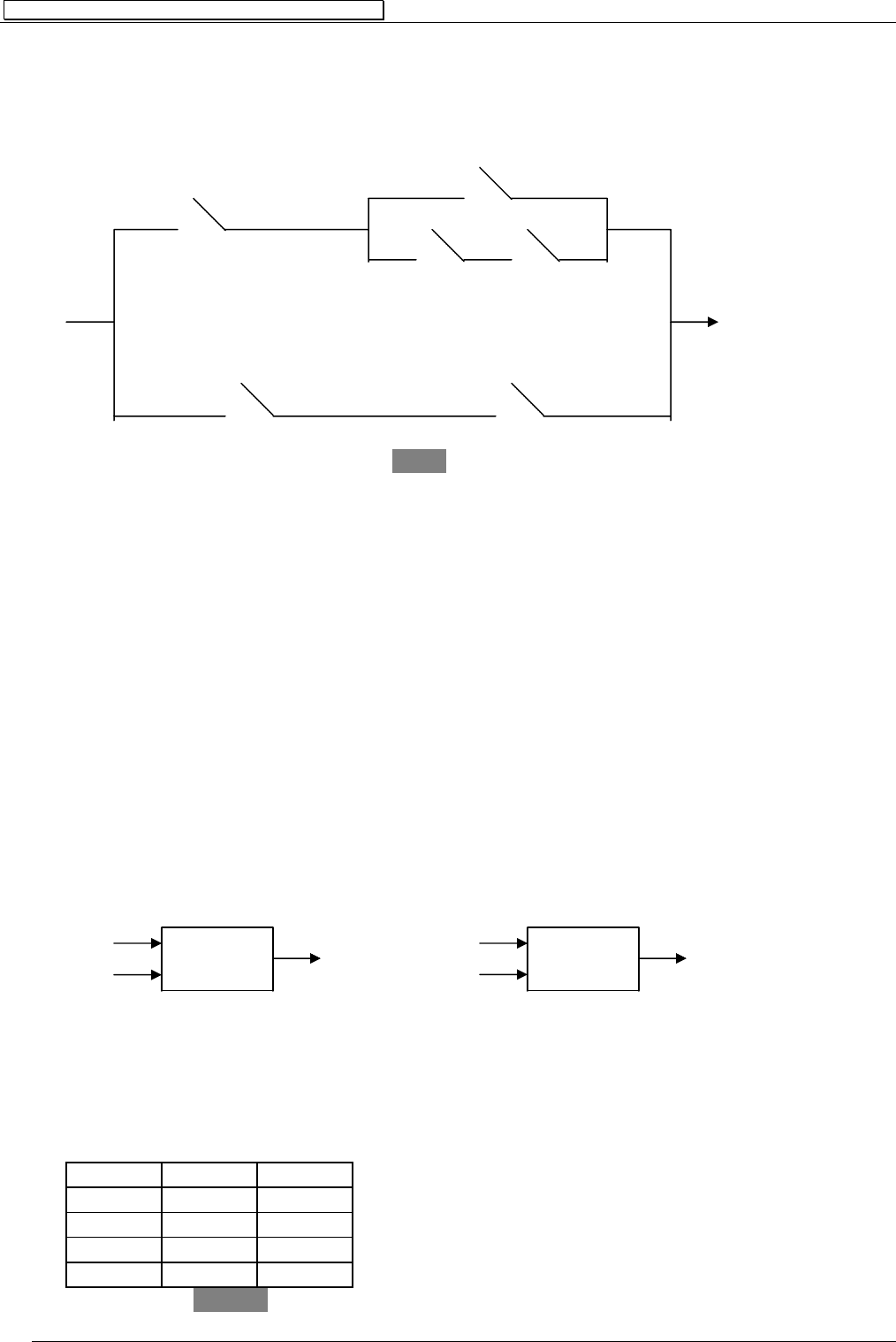
Тогда соответствующая ей схема примет вид, как показано на рис.2.

С D

B ⎤D

Рис.2

Две схемы считаются эквивалентными, если через одну из них проходит ток то-

гда и только тогда, когда он проходит через другую. Из двух эквивалентных схем бо-

лее простой считается та, которая имеет меньшее число переключателей.

Таким образом, аппарат исчисления высказываний можно использовать для ана-

лиза электрических схем (построения пропозиционных

формул прохождения тока че-

рез схему), синтеза схем (построения схем по заданной пропозиционной форме) и

упрощения схем (эквивалентные преобразования пропозиционных форм).

Комбинационные схемы.

Комбинационными схемами называют электрические схемы, построенные из ло-

гических элементов. Рассмотрим комбинационные схемы, построенные из элементов

трёх следующих типов:

• Конъюнкторы (элементы «И»). Обозначаются они следующим образом:

& И

или

Эти элементы имеют два входа и один выход. На каждый вход конъюнктора мо-

жет подаваться единичный или нулевой потенциал (напряжение). Единичный потен-

циал появляется на выходе тогда и только тогда, когда на каждом входе конъюнктора

присутствует единичный потенциал. Во всех остальных случаях на выходе нулевой

потенциал. Конъюнктор реализует

логическую операцию & (И) и его работа описыва-

ется следующей таблицей истинности:

0 0 0

0 1 0

1 0 0

1 1 1

Табл. 3

• Дизъюнкторы (элементы «или»). Обозначаются как

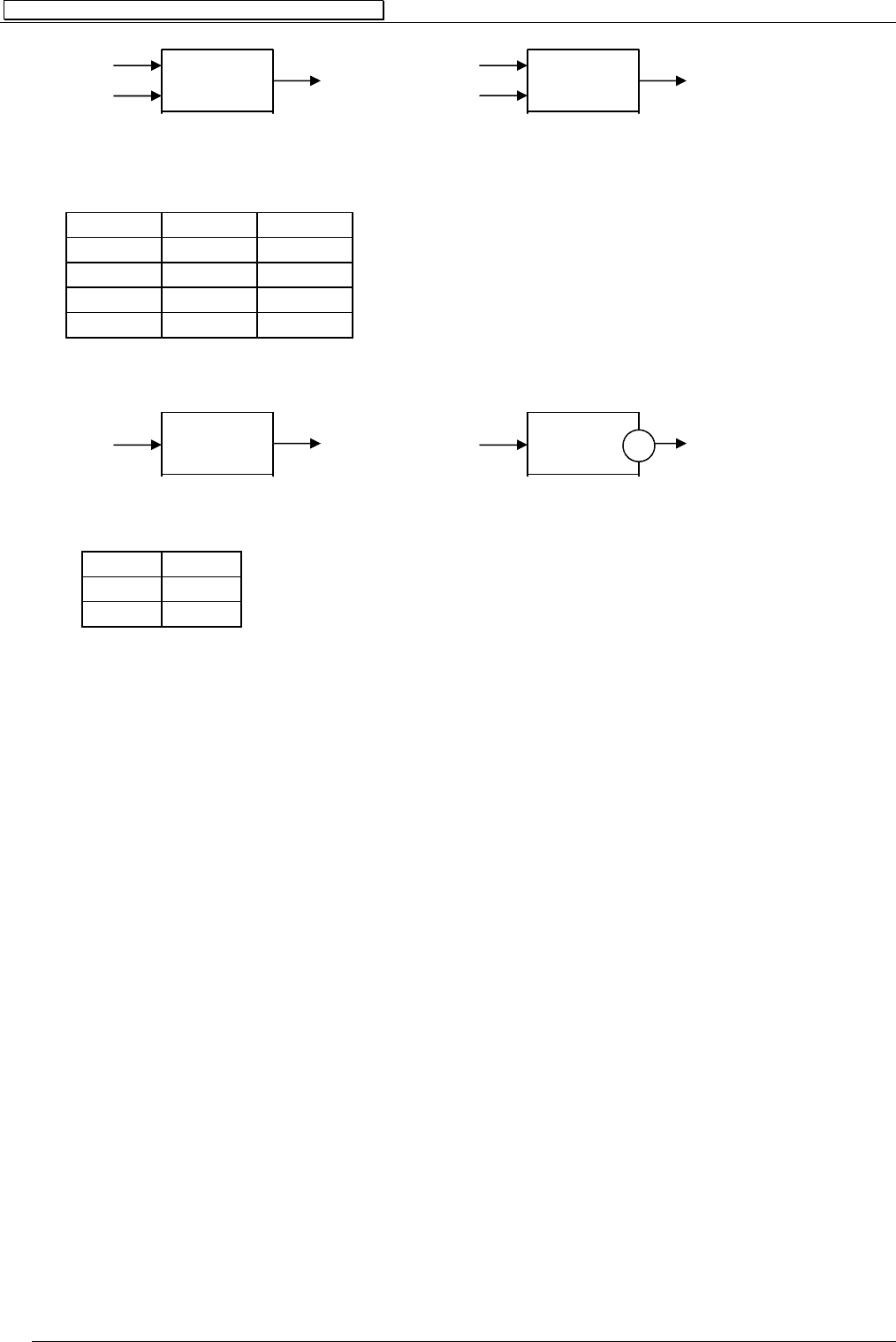
Математическая Логика и Теория Алгоритмов стр. 18 из 64

1 ИЛИ

или

Имеют два входа и один выход. Реализуют логическую операцию ∨ (ИЛИ) и их

таблица истинности имеет вид:

0 0 0

0 1 1

1 0 1

1 1 1

• Инверторы (элементы «НЕ»). Обозначаются как:

НЕ

или

Имеют один вход и один выход. Реализуют логическую операцию отрицания ⎤

(НЕ). Таблица истинности имеет вид:

0 1

1 0

Как нам уже известно, логический базис И, ИЛИ, НЕ является функционально

полным и на его основе можно реализовать любую логическую функцию, поэтому

комбинационные схемы из элементов И, ИЛИ, НЕ составляют базис для построения

современных устройств вычислительной техники.

Характерным признаком именно комбинационных схем (в отличие от автоматов с

памятью) является то,

что совокупность их выходных сигналов в любой момент вре-

мени однозначно определяется входными сигналами схемы в этот же момент времени.

Время при этом считается дискретным. Длительность одного дискрета (такта) выби-

рается равной или больше максимальной величины задержки элементов комбинаци-

онной схемы, которая в свою очередь определяется максимальной глубиной комбина-

ционной схемы

(т.е. числом последовательно включённых в схему логических эле-

ментов, каждый из которых имеет фиксированную величину задержки

τ (для совре-

менных схем

τ =1нс=10

-9

с)).

Математическая Логика и Теория Алгоритмов стр. 19 из 64

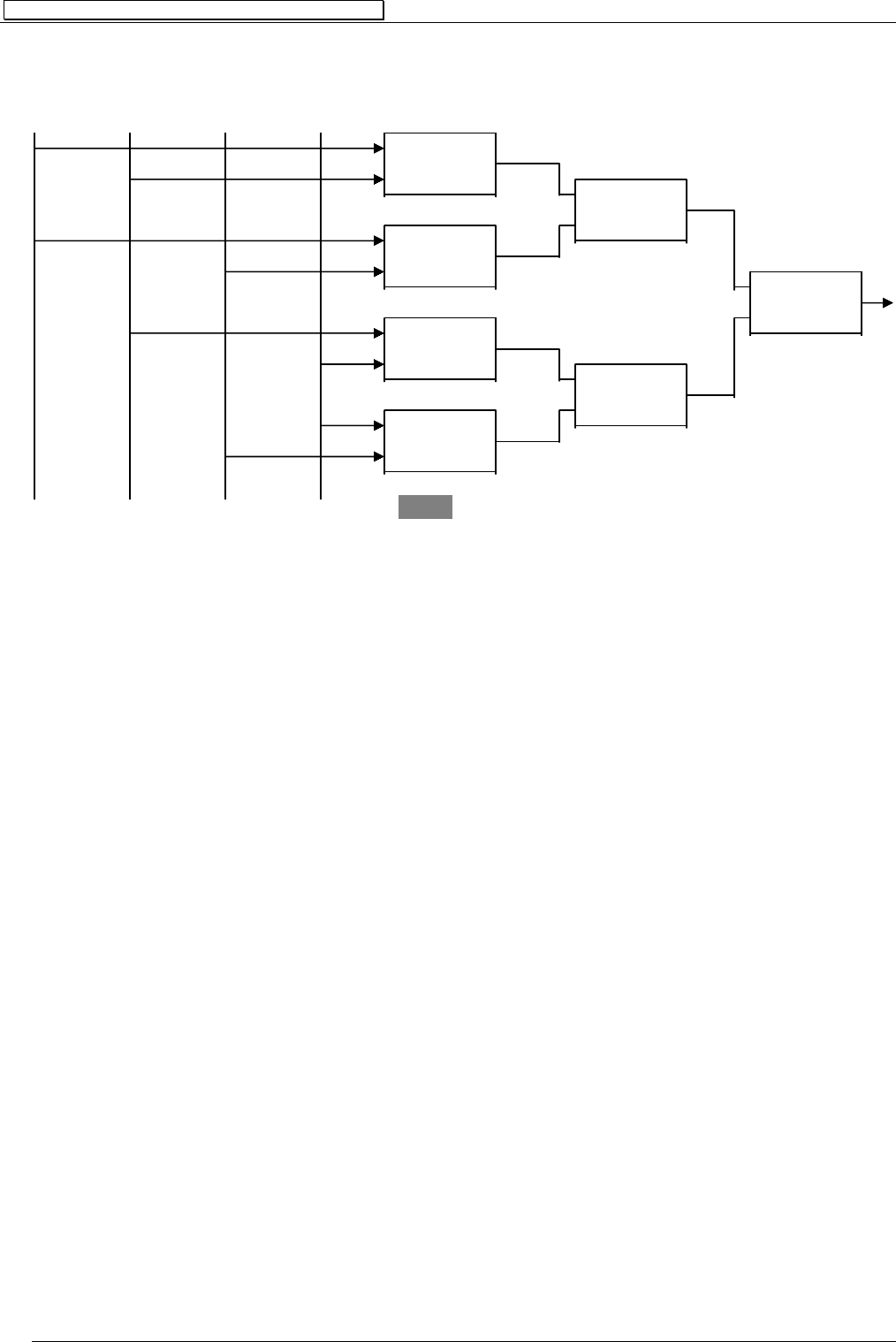
На рисунке 3 представлен пример комбинационной схемы:

Рис.3

Здесь глубина схемы равна 3 и её максимальная задержка 3

τ .

Пропозиционная форма описывающая логику работы этой схемы имеет вид:

Z=((X

∨X

)&(X

∨X

))&((X

∨X

)&(X

∨X

))

Также, как и для рассмотренных выше электрических схем, для комбинационных

схем важное значение имеют задачи анализа и синтеза таких схем на основе аппара-

та исчисления высказываний.

В результате решения задачи анализа комбинационной схемы требуется полу-

чить представление каждого выходного сигнала в виде пропозиционной формы, где в

качестве пропозиционных букв используются

символьные обозначения входных сиг-

налов. Для указанной выше комбинационной схемы мы эту задачу уже решили.

В результате решения задачи синтеза комбинационной схемы по заданным таб-

лично (таблица истинности) или в виде пропозиционных форм истинностным функци-

ям, отражающим зависимость выходных сигналов Z от значений входных сигналов X,

нужно построить комбинационную схему реализующую эти функции

. На этапе синте-

за комбинационной схемы решается также задача её максимального упрощения, т.е.

оптимизации.

Рассмотрим полученную в результате анализа комбинационной схемы (см. рис.3)

пропозиционную форму и попробуем её упростить, используя аппарат исчисления

высказываний.

((X

∨X

)&(X

∨X

))&((X

∨X

)&(X

∨X

))↔((X

∨X

)&X

∨(X

∨X

)&X

)&((X

∨X

)&X

∨(X

∨X

)&X

) ↔ (X

∨X

) & (X

∨X

) ↔ ((X

∨X

)&X

) & (X

&(X

∨X

)) ↔ (X

∨X

)

& (X

∨X

) ↔ (X

∨X

) & (X

)∨(X

∨X

)&X

↔ (X

)∨(X

) & (X

) ∨

) ∨ (X

) ↔ (X

∨X

) ∨ X

& X

∨ X

& X

↔ X

& X

∨ X

& X

∨

& X

↔ X

& X

∨ X

& X

)A()B()C()D(

Математическая Логика и Теория Алгоритмов стр. 20 из 64

Полученная в результате

эквивалентных преобразова-

ний пропозиционная формула

значительно проще исходной.

Синтезированная по этой фор-

муле комбинационная схема

имеет вид, как показано на

рис.4. Эта схема эквивалентна

схеме на рис.3, но значительно

проще её.

Рис.4

Наряду с рассмотренными выше примерами аппарат исчисления высказываний

широко использовался при создании систем искусственного интеллекта (автоматиче-

ское доказательство теорем), представление знаний и получение новых знаний в экс-

пертных системах и т.д. Перейдём теперь к рассмотрению другого важного раздела

математической логики, который непосредственно связан с исчислением высказыва-

ний и

получил название исчисление предикатов.

Исчисление предикатов.

Кванторы, формулы, выражения, свободные и связанные перемен-

ные.

Исчисление высказываний оперирует высказываниями, не вдаваясь в структуру

последних. Там мы изучали логические отношения между пропозиционными буквами,

которые различными способами при помощи операций &, ∨, ⎤, →, ↔ связывались ме-

жду собой, образуя более сложные пропозиционные формы (высказывания). При

этом нас не интересовала внутренняя структура блоков, из которых строились выска-

зывания. В тоже время не все виды логических рассуждений могут быть обоснованы и

представлены в рамках такого подхода. Например: Все люди смертны. Сократ чело-

век. Следовательно, Сократ смертен.

Такой вывод нельзя получить в рамках исчисления высказываний, т.к. здесь ис-

пользуется внутренняя структура предложений.

В исчислении предикатов можно реализовать выводы такого

типа. Для этого вво-

дятся две новые операции: ∀ (для любого, для всякого, для всех) и ∃ (существует,

для некоторого, существует по крайней мере один). Дадим им формальное определе-

ние.

Если P(X) означает, что X обладает свойством P, то посредством ∀X P(X) будем

обозначать утверждение: «для всякого или для любого X свойство P выполнено» или

«все

X обладают свойством P».

Запись ∃X P(X) означает, что «существует по крайней мере один X, обладающий

свойством P».

В выражении ∀X P(X) часть ∀X называется квантором всеобщности, а часть ∃X в

выражении ∃X P(X) называется квантором существования.

С помощью этих кванторов представленное выше умозаключение можно фор-

мально записать в виде:

∀X (Ч(X)→C(X))

Ч(X)

C(X)

Дадим теперь определение формул и выражений исчисления предикатов.

Для построения выражений будем использовать те же символы, что и в исчисле-

нии высказываний: запятые, скобки, знаки ⎤, →; вместо пропозиционных букв будут

использоваться их обобщения – предикатные буквы

A,...,A , а также предметные