Галуев Г.А. Математическая логика и теория алгоритмов

Подождите немного. Документ загружается.

Математическая Логика и Теория Алгоритмов стр. 41 из 64

Сформулируем теперь алгоритм унификации:

1 К=0, множество

WW , (пустое)

2 Если

W - единичный дизъюнкт, то

это НОУ для W, конец алгоритма.

В противном случае найдем множество

D рассогласования для

W .

3 Если существуют такие элементы

t , то переход к п.

4 .

⎭

⎬

⎫

⎩

⎨

⎧

οσσ

⎭

⎬

⎫

⎩

⎨

⎧

(т.е. каждый элемент в

1+k

W получается применением подстановки

⎭

⎬

⎫

⎩

⎨

⎧

к со-

ответствующему элементу из

W ).

5 1+= kk Переход к п.

. Если две или более литер (с одинаковым знаком инверсии) дизъ-

юнкта

C имеет НОУ

, то

C называют склейкой. Если

C - единичный дизъюнкт, то

склейка называется единичной склейкой.

Например: пусть

C есть )())(()( xVQxfVPxP . Тогда литеры )(xP и ))(( yfP имеют

НОУ

{

}

yf )(

. Значит ))(())(( yfQVyfP ¬ - есть склейка C т.е.

C .

. Пусть

C и

C два дизъюнкта (дизъюнкты посылки), которые не

имеют общих переменных. Пусть

L и

L две литеры в

C и

C соответственно. Если

L и

имеют НОУ

, то дизъюнкт

σσ

VCC , где

C (или

C ) получается выражением из

C (

) примера

(или

), называется бинарной резольвентой

. Резольвентой дизъюнктов посылок

C и

C является одна из сле-

дующих резольвент:

- бинарная резольвента

C и

C ;

- бинарная резольвента

C и склейки

C ;

- бинарная резольвента склейки

C и

C ;

- бинарная резольвента склейки

C и склейки

C .

Метод резолюций заключается в применении правила резолюций, которое поро-

ждает резольвенты для множества дизъюнктов.

Этот метод полон, т.е. для любого невыполнимого множества дизъюнктов можно

породить пустой дизъюнкт.

Рассмотрим пример работы этого метода.

Пусть имеется множество формул

F есть ))(&)()(( xRxWxCx →∀

F есть

)(&)( xQxxC∃

G есть )(&)( xRxxQ∃

Докажем с помощью метода резолюций, что

G является логическим следстви-

ем

F и

F , т.е. нужно доказать, что GFF ⎤&&

противоречиво. Преобразуем

F ,

F и

G⎤ в стандартную (скулемовскую) формулу.

Для

F имеем ))()((&)()(( xVRxCxVWxCx ⎤⎤∀

для

F имеем )(&)( aQaC

для

G⎤ )()( xRVxQx ⎤⎤∀ следовательно множество дизъюнктов S есть

Математическая Логика и Теория Алгоритмов стр. 42 из 64

)()( xVWxC⎤

2 )()( xVRxC⎤

)(aC S

4 )(aQ

5 )()( xRVxQ ¬⎤

Тогда

6 )(aR резольвента

2 и

7 )(aR⎤ резольвента

4 и

0 резольвента

Таким образом,

G действительно является следствием

F и

F .

Лекция 8.

Теория алгоритмов.

Слово алгоритм связывают с именем арабского математика IX века Мухаммеда

ибн Муса Аль-Хорезми, впервые выдвинувшего идею о том, что решение любой по-

ставленной математической и философской задачи может быть оформлено в виде по-

следовательности выполняемых правил, то есть алгоритмизировано. Алгоритм А

действует на некотором множестве объектов {a} и представляет собой некоторую оп

ределенную последовательность действий (простейших), выполнение которой либо

заканчивается и получается объект А(а), либо процедура эта никогда не заканчива-

ется, либо обрывается без получения значения А на а. Такое интуитивное понятие

алгоритма долгое время устраивало математиков и было достаточным для установле-

ния того, является ли данное предписание(последовательность действий) алгорит-

мом, особенно если идет речь о построении конкретных алгоритмов для решения кон-

кретных задач. Однако, как только мы, придя к предположению о возможной нераз-

решимости какой-либо алгоритмической проблемы, начнем пытаться доказывать, что

эта неразрешимость действительно имеет место, мы в общем случае сразу же столк-

немся с необходимостью уточнения понятия алгоритма

его стандартизации. Осозна-

ние этого факта и широкие исследования области оснований математики (аксиомати-

ческие теории множеств в исчислении высказываний предикатов) привели к появле-

нию в 30-е годы сразу нескольких уточненных понятий алгоритма:

А. Чёрч - λ-конверсии Чёрча, рекурсивные функции Эрбрана-Геделя-Пливей

комбинаторные процессы Поста, машины Тьюринга, позднее нормальные алгоритмы

Маркова А. А..

Произведенное уточнение понятия алгоритма дало немедленный эффект. В 1936 году

Чёрчем была доказана неразрешимость знаменитой проблемы – разрешимости для

классического исчисления предикатов, которую в то время Гильберт считал главной

проблемой математической логики.

В 1947 году А. А. Марковым на основе понятия нормального алгоритма была ус-

тановлена неразрешимость проблемы ТУЭ – проблемы тождества

для полугрупп, то

есть первый пример неразрешимой алгоритмически проблемы собственно математи-

ческого характера.

Особенно возросла роль понятия алгоритма с появлением ЭВМ и созданием ал-

горитмических языков программирования. Собственно теория алгоритмов стала осно-

вой современной вычислительной математики и программирования.

Наиболее существенным для оправдания появления различных уточнений по-

нятия алгоритма оказалось совпадение

классов вычислимых функций для всех этих

понятий. Оказалось, что все эти понятия сводимы друг к другу, то есть эквивалентны.

В тоже время наличие различных понятий алгоритма имеет и свои преимущества, так

как для различных классов задач бывает удобнее использовать и различные понятия

алгоритма (также как различные языки программирования ориентированы на разные

классы задач).

Математическая Логика и Теория Алгоритмов стр. 43 из 64

Рассмотрим теперь различные уточненные формулировки понятия алгоритма и пока-

жем взаимосвязь между ними.

Алгоритмические системы.

Введем ряд понятий и определений. Пусть имеем непустое множество А, кото-

рое назовем алфавитом или словарем, а его элементы – символами или буквами. На-

пример, алфавит А={+, ?, r, a, b, z}. Он содержит шесть букв.

Произвольную конечную последовательность букв будем называть словом или

цепочкой в этом алфавите. Слово считается ориентированным слева - направо. На-

пример, последовательность А

=+a+b? является словом, а последовательность B=z+a-

b? не является словом (так как знак '' - '' отсутствует в А) в алфавите А . Слово, не

содержащее никаких букв называется пустым и обозначается Е.

Число букв, входящих в слово, называется его длиной, длина А=5 и обознача-

ется

A . Ясно, что E =0.

Пусть А* - множество всех слов в алфавите А, и пусть А, В

∈

А*. Упорядоченной

паре <А,В> поставим в соответствие слово С, полученное приписыванием к слову А

слова В. Говорят, что слово С получено конкатенацией(умножением) А и В и записы-

вают С=АВ. Таким образом, конкатенация это с одной стороны операция приписыва-

ния А к В, а с другой – результат этого

приписывания, то есть С=АВ.

Пусть А=cacb и B=abb, тогда С=cacbabb=АВ, а ВА=abbcacb. Длина конкатена-

ции С равна сумме образующих ее слов.

Ясно, что конкатенация является всюду определенной и ассоциативной, но не

коммуникативной операцией, то есть для любых А, В, С

∈

* имеет место:

А(ВС)=(АВ)С=АВС и АВ

≠ ВА. Кроме того, АЕ=ЕА=А, где Е играет роль единич-

ного элемента. Поэтому множество

* по операции конкатенации является свобод-

ной полугруппой над

A . Причем элементы A являются образующими этой полугруп-

пы.

Пусть P, Q, A, X, Y различные слова в алфавите

A и пусть А=XPY. Тогда слова

типа X; P; Y называются вхождениями в слово А. Слова типа X; XP; PY – называются

подсловами слова А.

Пусть имеется подстановка вхождения слова Q место слова Р и наоборот, то

есть P~Q. Тогда слову А можно поставить в соответствие слово В и наоборот, из сло-

ва В получить слово А.

Например, Р=

⎣⎦

apa Q=

⎣⎦

ло . Тогда слову А= п

⎣

⎦

ара д соответствует слово

В=п

⎣⎦

ло д.

То есть имеются два вхождения P и Q в слова А и В. такие, что вместо Р в слово

А можно подставить Q и получить слово В и наоборот.

Такие соотношения называются соотношениями ТУЭ (по имени норвежского ма-

тематики Акселя Туэ).

Они приводят (соотношения ТУЭ) к одному из вариантов ассоциативного исчис-

ления.

Два

слова А и В называются смежными, если одно из них получено из другого

однократным применением соотношений ТУЭ. В общем случае, можно допустить не-

сколько последовательных применений соотношений ТУЭ. Пусть А – некоторый алфа-

вит и R:

~ QP , …,

QP ~ - система соотношений ТУЭ.

Говорят, что слово

B соотносимо со словом

B , если существует последовательность

слов

BB ,...,

, таких, что

B смежно с

1−i

B для i= 1,…,p.

Будем считать, что любое слово соотносимо с самим собой. Тогда соотносимость будет

рефлексивным, симметричным и транзитивным отношением, то есть отношением эк-

вивалентности. Это позволяет соотносимые слова называть эквивалентными и обо-

Математическая Логика и Теория Алгоритмов стр. 44 из 64

значать знаком ≈. Легко видеть, что для любых слов X и Y из А≈В следует

XAY≈XBY.

А. Туэ ещё в 1914 году сформулировал следующую проблему, известную под

названием ''проблемы тождества для полугрупп'', которая (для 5конечной опреде-

ленной полугруппы, допускающей простую и естественную конструктивизацию в виде

понятия ассоциативного исчисления) трансформируется в ''проблему эквивалентно-

сти'': для любой пары слов в некотором алфавите установить, являются они эквива-

лентными или нет. Рассмотрим более подробно этот вопрос. Введем ряд определений.

. Слово

1−

A называется обращением (инверсией) слова А, если оно

образовано в точности из тех же вхождений, что и А, но взятых в обратном порядке.

Слово А называется симметричным, если оно совпадает со своей инверсией.

Рассмотрим некоторое ассоциативное исчисление в алфавите А={a,b}, опреде-

ляемое соотношениями aa~E, bb~E. Сократить слово А в этом исчислении, значит об-

разовать новое слово В, смежное с А (то есть В получаем из А однократным примене-

нием соотношения ТУЭ), которое короче А. Взяв некоторое слово за исходное, мы

можем путем последовательных сокращений, образовать ряд слов, который приведет

к несократимому слову(возможно пустому).

Например: Пусть A=aabbaaabbbabbb, B=abab, C=aaabbabbbaab. Покажем один из

вариантов сокращения слова А

aa~E bb~E

Тогда ⎣aa⎦bbaaabbbabbb≈⎣bb⎦aaabbb a bbb≈⎣aa⎦abbbabbb≈a⎣bb⎦babbb≈aba⎣bb⎦b≈abab. В

результате получаем, что А эквивалентно В, а В является несократимым в этом ис-

числении. Для слова С существует несколько вариантов сокращения, один из кото-

рых имеет вид

⎣aa⎦abbabbbaab≈abbabbbaab≈aa⎣bb⎦baab≈⎣bb⎦

baab≈b⎣aa⎦b≈⎣bb⎦≈0=E. Поэтому C≈E.

Легко проверить, что результат не зависит от того, в каком порядке выполняются

сокращения. В каждом классе эквивалентности существует ровно одно несократимое

слово, которое называется каноническим представителем этого класса.

Для данного ассоциативного исчисления проблема эквивалентности разрешима, так

как любые два слова эквивалентны тогда и только тогда, когда они обладают одним и

тем же каноническим представителем, который легко найти путем реализации проце-

дуры последовательных сокращений.

Однако существуют примеры ассоциативных исчислений, для которых проблема эк-

вивалентности неразрешима.

Например, A={a,b} aaa~aa, aba~aa, bab~bb, bbb~bb.

Из слова ababa можно

получить ⎣aba⎦ba≈a⎣aba⎦≈⎣aaa⎦≈aa или a⎣bab⎦a≈abba.

Слова aa и abba несократимы, эквивалентны, но различны.

Первые примеры ассоциативных исчислений, для которых проблема эквивалент-

ности неразрешима, были получены А. А. Марковым и Э. Л. Постом в 1947 году. В

связи с этим возникает вопрос: существует ли универсальный метод, позволяющий

решать

проблему эквивалентности. Путем введения уточненного понятия алгоритма –

нормального алгоритма Марков А. А. Показал, что в общем случае эта проблема не-

разрешима. Об этом мы будем говорить позже.

Комбинаторные системы.

Комбинаторные системы это частный случай формальных (алгоритмических)

систем. Они используются для исследования задач комбинаторного характера, свя-

занных с преобразованием слов.

Для определения комбинаторной системы необходимо задать:

1. Конечный алфавит А, называемый основным, и , возможно, вспомогательный

алфавит В. Из А

U В образуется множество

A слов (формул);

2. Выделенное непустое слово S(аксиому) S

∈

A U B.

Математическая Логика и Теория Алгоритмов стр. 45 из 64

3. Конечное множество правил вывода, задаваемых ориентированными подста-

новками.

В простейшем случае ориентированная подстановка имеет вид: А→В, где А и В

слова в алфавите A

U B. подстановка такого вида является бесконтекстной, называет-

ся полутуэвской и означает, что слово А заменяется словом В. ясно, что обратная

подстановка В→А также является полутуэвской. Если имеются одновременно прямая

А→В и обратная В→А подстановки, то их можно заменить одной неориентированной

подстановкой, которая обозначается А~В и называется туэвской.

При наличии кон-

текста полутуэвская подстановка имеет вид PAQ→PBQ, где P и Q некоторые(возможно

и пустые) в том же алфавите, что А и В.

Ориентированная подстановка AP→PB называется нормальной, обратная к ней

подстановка PB→AP называется антинормальной. Совокупность нормальной и анти-

нормальной подстановок, то есть неориентированная подстановка вида AP~PB назы-

вается постовской.

Таким образом

, в зависимости от используемой подстановки, можно рассматривать

следующие 4 вида комбинаторных систем: полутуэвская, туэвская, нормальная и по-

стовская.

Например: пусть задана полутуэвская система, в которой А={a,b} – основной

алфавит, B={s} - вспомогательный алфавит, состоящий из одной буквы – аксиомы s,

и три подстановки

1) s→ab 2) s→asb 3)s→bsa.

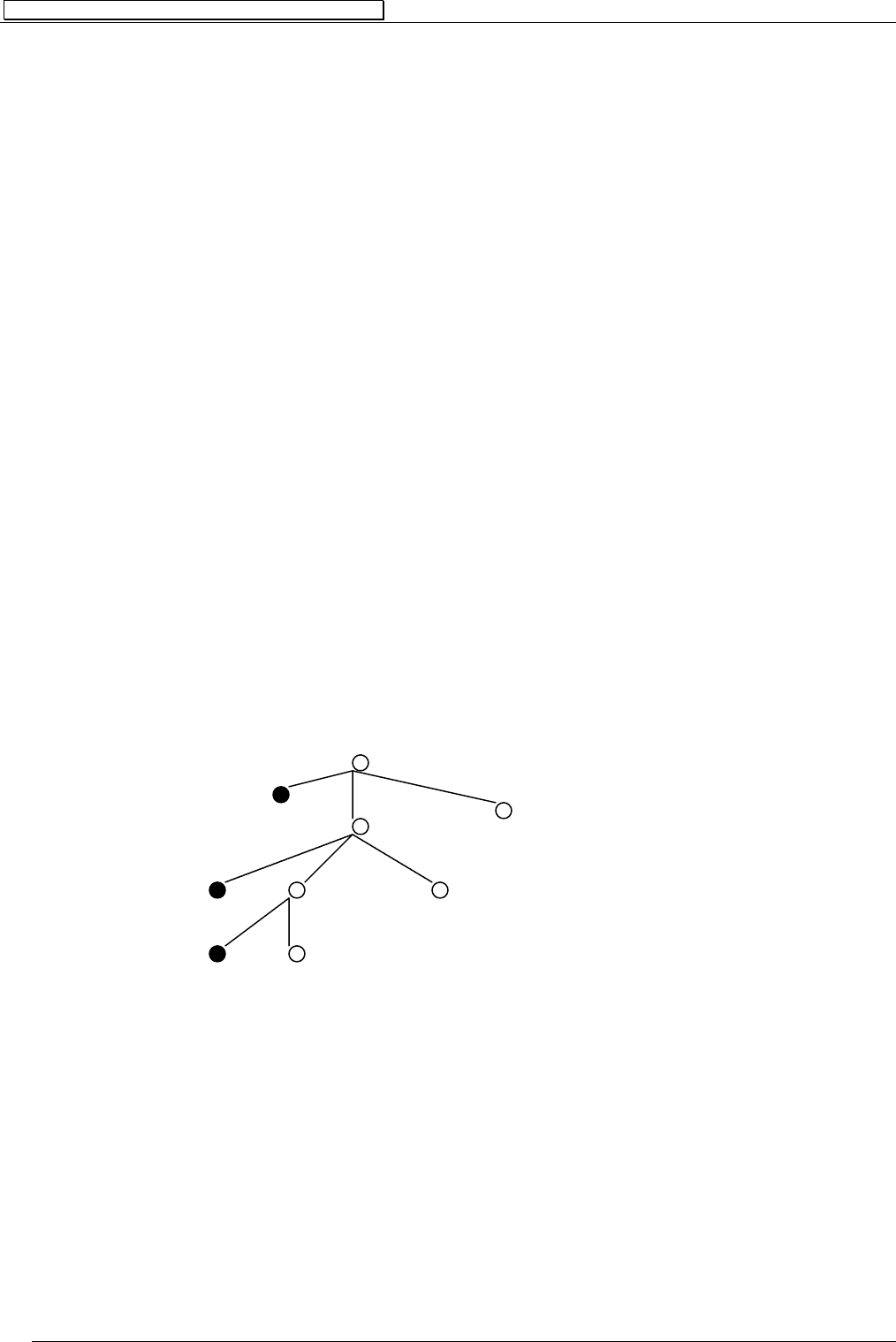
Тогда множество всех формул, выводимых в этой системе из

аксиомы s с помо-

щью заданных подстановок можно представить в виде бесконечного ориентированно-

го графа, каждая вершина которого помечена некоторым словом из алфавита A

U B.

Дуги (ребра) графа помечаются номером подстановки. Фрагмент такого графа пока-

зан ниже

В любую вершину графа, полученную формулой из вершины S ведет один путь.

Он (этот путь или эта ветвь графа) как раз и соответствует выводу этой формулы.

Например, вывод формулы aaabbb из S имеет вид

⎯→⎯

asb ⎯→⎯

aasbb ⎯→⎯

aaabbb.

Для вершин графа помеченных только буквами алфавита А={a,b}. Вывод фор-

мулы в данной комбинаторной системе продолжен быть не может (вершины такие за-

штрихованы).

Комбинаторная система называется моногенной (однозначной), если к любой ее

формулы может быть применено не более одной подстановки.

Комбинаторная система называется неоднозначной, если в ней имеется формула, для

которой существует по крайней мере два различных вывода.

bsa

absab

asb

aasbb

aab

aaasbbb

aaabbb

Математическая Логика и Теория Алгоритмов стр. 46 из 64

Например: Пусть имеется нормальная система с алфавитом А={a,b}, аксио-

мой bba и подстановками 1)aP→Pbba; 2)bP→Paba, где P - некоторое слово в алфавите

А.

Ориентированный граф, задающий множество всех выводимых формул имеет вид

Эта нормальная система является моногенной.

Например: Пусть имеется полутуэвская система с алфавитом А={a,bc}, B={s},

где s – аксиома, и подстановками : 1) s→as; 2) s→sb; 3) s→asb; 4) s→c.

Если изобразить граф выводимых в данной системе формул, то можно убедиться,

что формула acb является неоднозначной, так как для нее существует три разных вы-

вода.

1.S

⎯→⎯

as ⎯→⎯

asb ⎯→⎯

acb

2.S

⎯→⎯

sb ⎯→⎯

asb ⎯→⎯

acb

3.S

⎯→⎯

asb ⎯→⎯

acb

Поэтому эта полутуэвская система является неоднозначной.

Лекция 9.

Соответствие между полутуэвской и нормальной системой.

Пусть задана полутуэвская система П, состоящая из алфавита А={a,b,c}, слова

∈А – аксиома и подстановок QPBQPA

→ ( mi

≤

1 ). Добавим в алфавит А буквы со

штрихами и получим алфавит В={a,b,c,a',b',с'}. построим нормальную систему N,

включающую алфавит В, ту же аксиому

C , сопряженную с С и следующие подстанов-

ки:

1) aP→Pa', bP→Pb', cP→Pc' ;

2) a'P=Pa, b'P→Pb, c'P→Pc;

PBPA → ' mi

≤

≤1

Заметим, что подстановки типов 1) и 2) позволяют переставлять некоторую бу-

кву из начала слова в его конец, меняя при этом её ''штриховость'' на обратную.

Например, применяя к слову baab подстановки 1) и 2) можно получить циклический

вывод:

baab

⎯→⎯

aabb` ⎯→⎯

abb`a` ⎯→⎯

bb`a`a` ⎯→⎯

b`a`a`b` ⎯→⎯

a`a`b`b ⎯→⎯

a`b`ba

⎯→⎯

b`baa ⎯→⎯

baab.

Все слова в этой цепочке называются сопряженными. Каждая совокупность со-

пряженных слов образует класс эквивалентности. Заметим, что среди всех слов, со-

пряженных со словом А, есть и А'. Поэтому подстановки 1) и 2) позволяют за не-

сколько шагов переставлять слова из начала в конец.

Все слова, имеющие форму PQ' или P'Q; где P,Q

∈

A*, сопряженные со словом

из А* и только с ними, называются регулярными

В классе эквивалентности, рассмотренном выше, не существует регулярных слов. А

в классе эквивалентности:

abba

⎯→⎯

bbaa` ⎯→⎯

baa`b` ⎯→⎯

aa`b`b` ⎯→⎯

a`b`b`a` ⎯→⎯

b`b`a`a ⎯→⎯

b`a`ab

⎯→⎯

a`abb ⎯→⎯

abba

Математическая Логика и Теория Алгоритмов стр. 47 из 64

все слова, кроме слов abba и a'b'b'a', являются регулярными.

. Всякая формула системы П является формулой из системы N.

Доказательство.

Очевидно, что теорема справедлива для аксиомы С , так как она спряжена с

C .

Поскольку все формулы выводятся из аксиомы С, достаточно показать, что свойство

''быть формулой системы N'' сохраняется при применении подстановок системы П.

Предположим, что формула X системы П является формулой в системе N. Для

того, чтобы формула Х имела следствие в системе П, необходимо, чтобы Х могла быть

представлена в виде

QPAX

. Тогда в соответствии со схемой подстановок в системе

П из Х непосредственно следует

QPBY

= . На основе подстановок типа 1) системы N

из Х может быть получено слово

PQA

′

, которое является формулой в системе N, так

как оно сопряженное с Х.

Применяя к

QPA подходящую подстановку типа 3), системы N, мы можем по-

лучить слово

QPB , которое также является формулой в системе N. Слово ''

BQP со-

пряжено со словом Y . Действительно,

QPBPBQPQBQBPBpQ

iiiii

⎯→⎯

′

⎯→⎯

′′

⎯→⎯

′′′

⎯→⎯

′

2221

Поэтому слово Y, также является формулой системы N, что доказывает теорему.

. Всякая формула в системе N является регулярным словом, со-

пряженным с некоторой формулой системы П.

Доказательство.

Теорема справедлива для аксиомы

, поскольку она является регулярным

словом в силу способа построения слова, сопряженного с аксиомой С. поэтому доста-

точно доказать, что свойства регулярности и сопряженности с некоторой формулой

системы П сохраняются при использовании системы N. Сохранение указанных

свойств очевидно для подстановок 1) и 2). Рассмотрим подстановки типа 3). Предпо-

ложим, что формула

регулярна и сопряжена с некоторой формулой системы П.

Из регулярности

следует, что она может быть записана в виде

PPA

, где

P и

-некоторые слова в алфавите А. Единственное спряженное с

слово в системе П

это слово

PAP

. Из сделанного предположения следует, что слово

PAP

является

формулой в системе П. Однако слово

PAP

сопряжено со словом ''

21 i

BPP , которое мо-

жет быть получено с помощью подстановки 3)(

PBPA → ) из слова

PPA

. Очевидно,

что слово

21 i

BPP является регулярным. Следовательно, теорема доказана.

Таким образом, сформулированные теоремы показывают, что для любой полу-

туэвской системы можно построить нормальную систему, в классах эквивалентности

которых содержатся все формулы исходной полутуэвской системы. Легко показать,

что можно установить соответствия между полутуэвской и туэвской, нормальной и по-

стовской, а следовательно между туэвской и постовской

системами.

Отсюда видно, что множество всех выводимых слов А* в некоторой комбинаторной

системе(туэвской, постовской и т. д.) порождает ассоциативное исчисление в алфави-

те А, а ее подстановки задают так называемый алфавитный оператор ϕ, отображаю-

щий слова из А* в слова из А*. Этот алфавитный оператор еще не является алгорит

мом так как в ассоциативном исчислении не определен порядок применения подста-

новок: нормальные алгоритмы Маркова, вычислимые функции машины Тьюринга, то

есть способы, дающие уточненное (а не интуитивное ) понятие алгоритма. Рассмот-

рим их более подробно.

Нормальные алгоритмы Маркова.

Пусть задана полутуэвская система с алфавитом А={a,b,c} и системой подста-

новок вида: сb→a; ab→b; cba→cca; cca→baa; baa→cba. Порядок их применения сле-

Математическая Логика и Теория Алгоритмов стр. 48 из 64

дующий: исходя из произвольного слова Р, система подстановок просматривается в

естественном порядке. Отыскивается первая подстановка, левая часть которой вхо-

дит в Р. Если таковой не имеется, то процесс обрывается; в противном случае (най-

дена подстановка), выполняется подстановка первого вхождения. В результате полу-

чаем новое слово

P . Для

P выполняется аналогичная процедура и так далее до тех

пор, пока на n-м шаге для слова

P процесс не оборвется. Таким образом имеем не-

который алгоритм переработки слов в алфавите А.

Этот алгоритм перерабатывает слово P=cbbabcb в слово bba:

babcb→ababcb→babcb→bbcb→bba (Слово просматривается слева направо, и под-

становки просматриваются в естественном порядке). Дальнейшие подстановки невоз-

можны. Однако слово Q=cbbcba. Не может быть переработано, так как получается

бесконечная последовательность:

bcba→abcba→bcba→bcca→bbaa→bcba→bcaa→bbaa→bcba→bcaa…

поэтому к слову Q алгоритм не применим.

В нормальном алгоритме Маркова порядок применения подстановок следующий. Ис-

ходя из произвольного слова Р, все подстановки просматриваются в естественном по-

рядке. Находится подстановка с левой частью, входящей в

P . Если таковой нет, то

процесс обрывается. В противном случае берется первая из таких подстановок и вы-

полняется замена ее правой части вместо первого вхождения ее левой части в Р, что

дает новое слово

. Для

выполняется аналогичная процедура и так далее. Про-

цесс оканчивается тогда, когда получим слово

P такое, что к нему не применима ни

одна подстановка или когда применяется подстановка, объявленная последней.

Как видно, в отличие от предыдущего алгоритма Маркова остановка может на-

ступать в двух случаях. Если в приведенной выше полутуэвской системе объявим

подстановку baa→cba последней, то ясно, что слово Q будет переработано в слово

bcba.

Гипотеза Маркова

. Всякий алгоритм в алфавите А эквивалентен некоторому

нормальному алгоритму в том же алфавите.

Эта гипотеза позволяет строго проводить доказательство алгоритмической не-

разрешимости того или иного круга проблем.

Рассмотрим в качестве примера доказательство алгоритмической неразрешимости

проблемы самоприменимости алгоритма.

Пусть в некотором алфавите А={

aaa ,...,,

} задан нормальный алгоритм Г. в

записи подстановок, кроме букв алфавита А, содержаться символы ''→'' и

'',''(запятая). Обозначив эти символы буквами

1+n

a и

2+n

a получим возможность изо-

бражать алгоритм Г словом в расширенном алфавите А*={

211

,,,...,

++ nnn

aaaa }. Приме-

ним теперь алгоритм Г к слову которое его изображает.

Если алгоритм Г перерабатывает это слово в некоторое другое слово, после че-

го наступает остановка, то это означает, что алгоритм Г применим к собственной за-

писи. Такой алгоритм назовем самоприменимым

. В противном случае алгоритм будем

называть несамоприменимым

Естественно возникает задача распознавания самоприменимости: по записи

данного алгоритма определить самоприменим этот алгоритм или нет.

Решение этой задачи можно представить в виде построения некоторого нор-

мального алгоритма Δ, который будучи применен во всякой записи самоприменимого

алгоритма Г, перерабатывает эту запись в некоторое слово М, а примененный ко вся-

кой записи

несамоприменимый алгоритма Г, перерабатывает эту запись в некоторое

другое слово L. В этом случае по результату применения алгоритма Δ можно узнать,

является ли заданный алгоритм Г самоприменимым или нет.

Доказательство приведем от противного. Допустим, что алгоритм Δ построен.

Тогда путем некоторого изменения системы подстановок алгоритма Δ можно постро-

ить другой алгоритм Δ', который всякую запись несамоприменимого алгоритма по-

Математическая Логика и Теория Алгоритмов стр. 49 из 64

прежнему перерабатывает в слово L, а ко всякой записи самоприменимого алгоритма

неприменим (остановка никогда не наступает). Это приводит к противоречию.

Действительно, если Δ' самоприменим, то он применим к собственной записи в

виде слова, то есть остановка должна наступать. Но по построению алгоритма Δ' это

свидетельствует как раз о том, что Δ' несамоприменим

. Если же Δ' несамоприменим,

то по своему построению, он применим к своей записи, так как он применим к любой

записи неасамоприменимого алгоритма. Но это как раз и означает, что Δ' самоприме-

ним.

Полученное противоречие показывает, что алгоритм Δ' не может быть построен.

Отсюда вытекает, что проблема распознавания самоприменимости алгоритмически

неразрешима.

Таким образом, решая какую-либо задачу, приходится считаться с тем, что ал-

горитм для ее решения может существовать. Поэтому важным является не только по-

строение самого алгоритма, но и доказательство невозможности его построения. Ина-

че говоря существуют такие проблемы, которые нельзя решить с помощью формаль-

ных рассуждений и вычислений. Такие проблемы

требуют творческого мышления, ин-

туиции, предвосхищения и других свойственных пока только человеку качеств.

Нормальные алгоритмы Маркова являются хорошей моделью логических алго-

ритмов. В тоже время можно показать, что любой логический алгоритм можно свести

к вычислительному, то есть любую алгоритмическую проблему можно свести к вычис-

лению некоторой целочисленной функции от целочисленных

значений аргументов.

Действительно, пусть все перерабатываемые алгоритмом М Г условия сведены в по-

следовательность и пронумерованы целыми числами: .,...,,

10 n

AAA множество решений

объединим в последовательность

.,...,,

10 m

BBB

Мы можем теперь сказать, что любой алгоритм, перерабатывающий запись

A в

B , сводится к вычислению значений числовой функции )(nm

, в которой (после

перенумерации) мы можем иметь дело только с номерами записей и решений, то есть

алгоритм перерабатывает номер записи условий в номер записи решений. Таким об-

разом, мы имеем уже не логический, а численный алгоритм.

Очевидно, что если есть некоторый алгоритм, решающий исходную задачу, то

есть и алгоритм вычисления

значений соответствующей функции.

Таким образом, возможность построения любого алгоритма сводится к понятию

вычислимости функции. В свою очередь, понятие вычислимости функции можно фор-

мализовать с помощью машин Тьюринга. Рассмотрим более подробно понятие машины

Тьюринга, которое является еще одним уточненным (не интуитивным) понятием алго-

ритма.

Машины Тьюринга.

Машина Тьюринга (МТ) состоит из устройства управления, считывающей голов-

ки и бесконечной ленты.

Устройство управления способно принимать некоторое конечное множество состоя-

ний.

Лента разбита на ячейки, в которые заранее вносятся обрабатываемые данные,

записанные в символах некоторого заданного алфавита (в простейшем случае в каж-

дую ячейку заносится один символ).

Головка считывает данные

из ячейки, которая находится прямо перед ней (та-

кая ячейка называется рабочей) и осуществляется запись на ленту промежуточных

результатов, далее происходит сдвиг ленты вправо или влево (в простейшем случае

на одну ячейку).

Процесс работы МТ состоит в следующем. Устройство управления находится в

одном из состояний, головка обозревает рабочую ячейку и

считывает символ, запи-

санный в ней. Устройство управления анализирует этот символ и выдает команду, в

результате выполнения которой может быть изменено содержимое ячейки, а лента

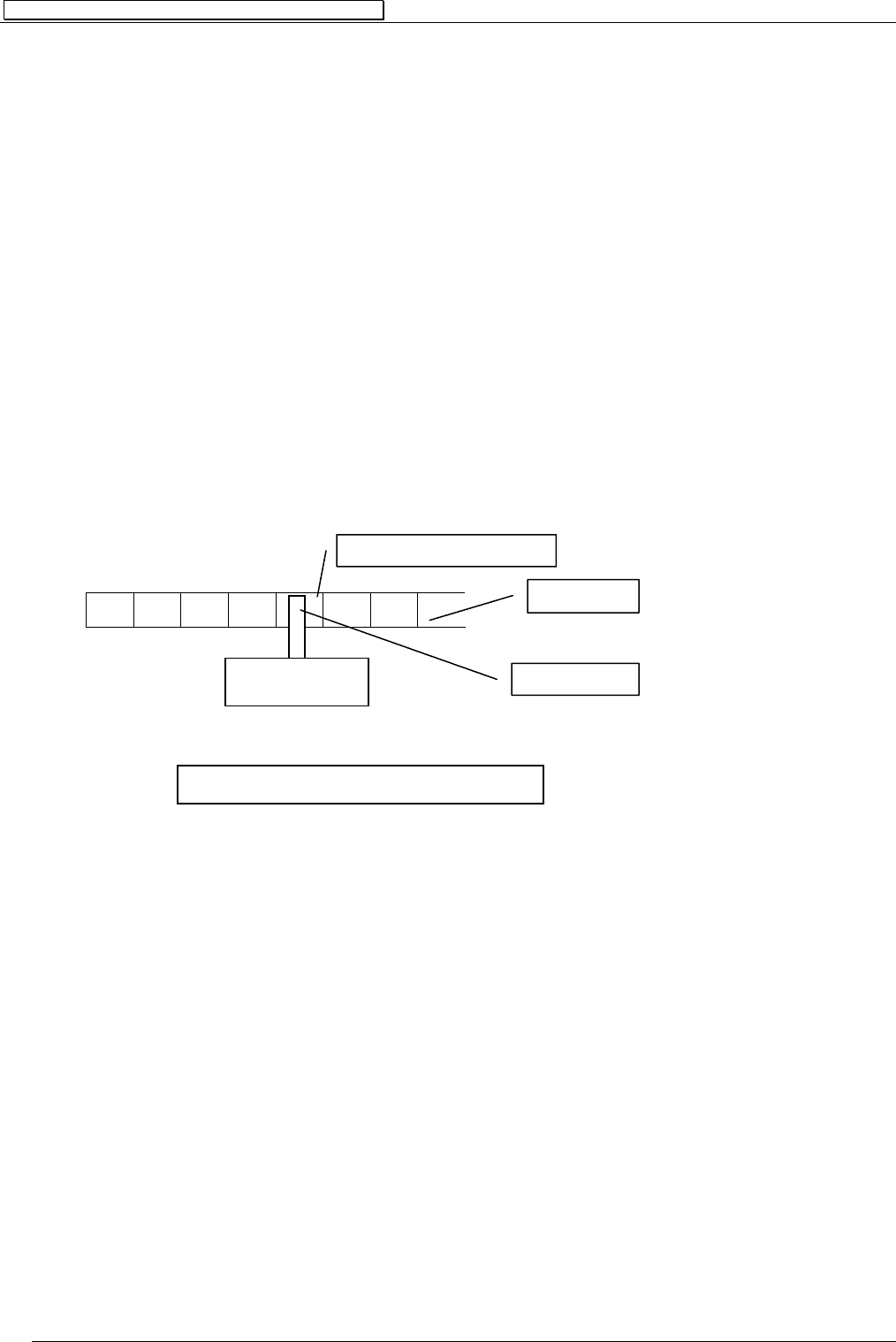
Математическая Логика и Теория Алгоритмов стр. 50 из 64

сдвинута вправо или влево. Конкретные действия определяются ситуацией, в которой

находится машина, и командами перехода.

Пусть

xxx ,...,,

- символы входного алфавита Х, буквы которого могут быть за-

писаны на ленте.

Символ

x отождествляется с нулевым символом. Иногда этот символ обозначается

как В и называется пробелом. Считается, что все незанятые ячейки ленты заняты

пробелами.

Пусть

},...,,{

10 m

qqqQ = - алфавит внутренних состояний устройства управления

МТ. Состояние

q - начальное состояние. Предполагается, что в исходном состоянии

МТ находится в состоянии

q , а считывающая головка обозревает крайний левый

символ входной цепочки.

Пусть

},,{ srlI = - множество инструкций управления движением ленты. Символ

l -означает сдвиг ленты на одну ячейку влево (

←

);

- сдвиг вправо, s - отсутствие

движения или остановка ленты. Заметим, что

l и

можно употреблять в противопо-

ложном значении, если полагать, что лента неподвижна, а движется головка считы-

вания.

МТ условно можно изобразить следующим образом

Ситуацией называется пара

XxQqxq

jiji

∈∈ ,; . Очевидно, начальная ситуация

МТ (указанной на рисунке) есть

. Выражением будем называть конечную после-

довательность символов в алфавите

},,,,...,,,,...,,{

1010

srlqqqxxx

Командой называется выражение одного из следующих типов

jlki

qxxq ;

jki

rqxq ;

jki

pqxq

;

jki

sqxq

- команда остановки.

Конечная последовательность команд, задающая функционирование МТ, назы-

вается таблицей Тьюринга. Если в таблице все команды имеют попарно различные

ситуации, то соответствующая ей МТ называется детерминированной.

Кроме того, функционирование МТ можно задавать с помощью так называемых

таблиц Айзермана, определяющих отображения

QвXQ ×:

, XвXQ ×:

IвXQ ×:

и называемых соответственно таблицами преобразования сигнала, за-

писи ленты и таблицей преобразования перемещения ленты. Эти три таблицы можно

объединить в одну обобщенную таблицу.

Конфигурацией называется выражение вида

lkji

xxxq ... , в котором

q не может

занимать крайней правой позиции.

Управляющее

устройство

Голо

ка

Рабочая ячейка

rl ←→

Ле

та

←→

- если движется головка