Galdi G.P. An Introduction to the Mathematical Theory of the Navier-Stokes Equations: Steady-State Problems
Подождите немного. Документ загружается.

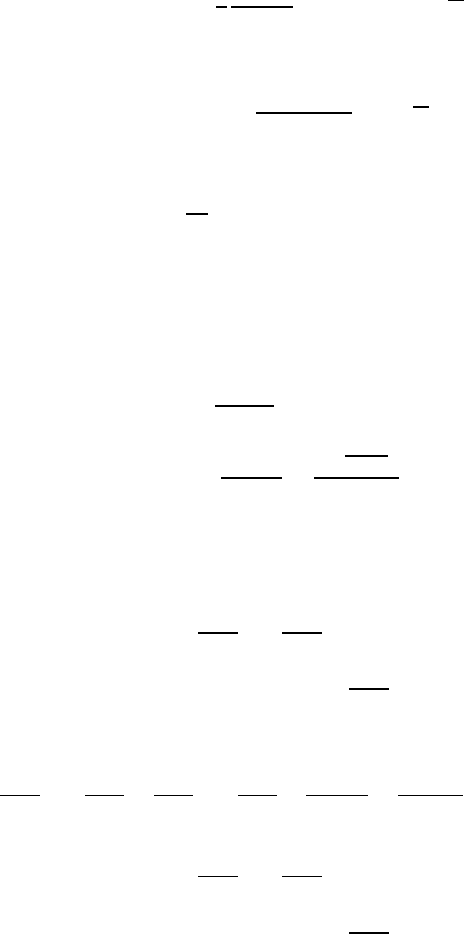
516 VIII Steady Generalized Oseen Flow in Exterior Domains
∆Ψ ≡
1
r
∂
2
(rΨ)
∂r
2
= −(4π s)
−3/2
e
−
r
2
4s
,
which gives, after a simple calculation and by fixing the integration constants
suitably,
Ψ(r, s) =
1
4π
3/2
r s
1/2
Z
r
0
e
−
ρ
2
4s
dρ . (VIII.3.6)
Moreover, from (VIII.3.6) it a lso f ollows that (Oseen 1927, pp. 40–41)
∂
∂s
+ ∆
ξ
Ψ(|ξ|, s) = 0 , s > 0 ,
so that from (VIII.3.2) we deduce γ
j
(x − y, t − τ ) = 0 for t > τ .
Collecting all the above informati on, we then conclude that the fundamen-
tal tensor Γ has the following form, for t > τ :
Γ
ij
(x − y, t −τ; R) = −δ
ij
∆Ψ(|x + R(t − τ )e
1
−y|, t − τ )
+
∂
2
∂y
i
∂y
j
Ψ(|x + R(t − τ)e
1
− y|, t −τ) ,
Ψ(r, t − τ ) =
1
4π
3/2
r
Z
r
0
e
−
ρ
2
4(t−τ)
(t − τ)
1/2
dρ ,
(VIII.3.7)
while γ = 0.
When R = 0, we set, for simpli city, Γ (ξ, s; 0 ) = Γ (ξ, s), ξ ∈ R
3
, s > 0.
Clearly, for t > τ , we have
∂Γ
ij
∂τ
− R
∂Γ
ij
∂y
1
+ ∆Γ
ij
= 0 ,
∂Γ
ij
∂y
i
= 0 ,
(VIII.3.8)
with “∆” operating on the y-variables, whereas, taking into account that
∂Γ
ij
∂τ
= −
∂Γ
ij
∂t
,
∂Γ
ij
∂y
k
= −
∂Γ
ij
∂x
k
,
∂
2
Γ
ij
∂y
k
∂y
`
=
∂
2
Γ
ij
∂x
k
∂x
`
, i, j, k, ` = 1, 2, 3 ,
we have
∂Γ
ij
∂t
− R
∂Γ
ij
∂x
1
− ∆Γ
ij
= 0 ,
∂Γ
ij
∂x
i
= 0 ,
(VIII.3.9)
where now “∆” operates on the x-variables .
The next result shows the way in which the tensor Γ = Γ (x −y, t −τ ; R)
becomes singular a t (x, t) = (y, τ). For its pro of we refer the reader to Oseen
(1927, §53).
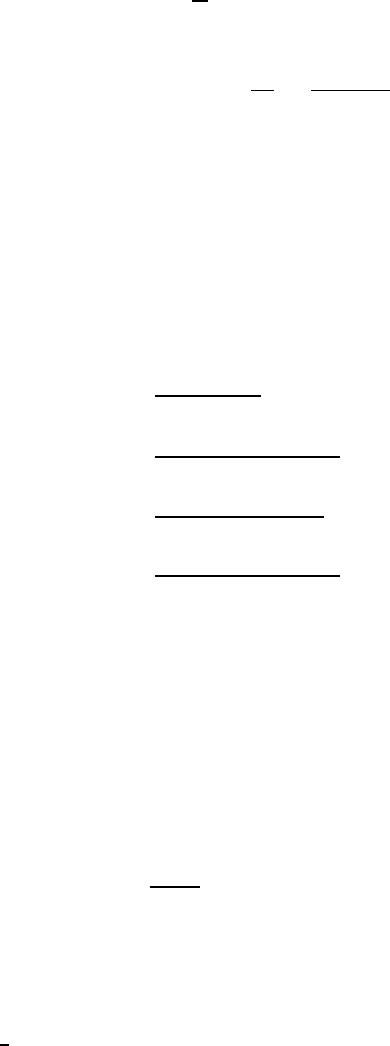
VIII.3 Fundamental Solution to the Time-Dependent Oseen Problem 517
Lemma VIII.3.1 Let A be a bounded, local ly Lipschitz domain and let u =
u(x, t) be a solenoidal vector field in C(A × [t − δ, t]), for some δ > 0. Then,
for a ll R ≥ 0,
lim
τ→t
−
Z
A
u
i
(y, τ)Γ
ij
(x−y, t−τ; R)dy = u
j
(x, t)−
1
4π
Z
∂A
(x
j
− y
j
)
|x − y|
3
u
i
(y, t)N
i
dσ
y
,
where N is the unit outer normal at ∂A.
An issue that is of basic importance to our aims is the study of suitable
asymptotic properties in space of the fundamental solution Γ and its spatial
derivatives. In order to reach this goal, we begin to recall the following result,
for whose proof we refer to Oseen (1927, §55, §73) and Solonnikov (1964,
Corollary in §5).
Lemma VIII.3.2 There exists a constant C > 0 such that the following
estimates hold, for a ll (τ, ξ) ∈ [0, ∞) ×R
3
− {(0, 0)}:
|D
2
ξ
Ψ(ξ, τ)| ≤
C
(τ + |ξ|
2
)
3/2
,
|Γ (ξ, τ ; R)| ≤
C
(τ + |ξ + Rτ e
1
|
2
)
3/2
,
|D
ξ
Γ (ξ, τ; R)| ≤
C
(τ + |ξ + Rτ e
1
|
2
)
2
,
|D
2
ξ
Γ (ξ, τ; R)| ≤
C
(τ + |ξ + Rτ e
1
|
2
)
5/2
.
With this result in hand, we can then prove the next one.
Lemma VIII.3.3 Let
Γ
`
(ξ; R) =
Z
∞
0
|D
`
Γ (ξ, τ; R)|dτ , ` = 0, 1, 2 ,
and set Γ
`
(ξ) := Γ
`
(ξ, 0), ` = 0, 1, 2. The following properties hold:
(i) If R = 0, we have, for all ξ ∈ R
3
− {0},
Γ
`
(ξ) ≤
C
|ξ|
`+1
, ` = 0, 1, 2 , (VIII.3.10 )
with C = C(`) > 0 .
(ii) If R > 0, let
s(ξ) = |ξ|+ ξ
1
, ξ ∈ R
3
, (VIII.3.11)
and 0 < β <
1
2
. Then, for all ξ ∈ R
3
−{0},
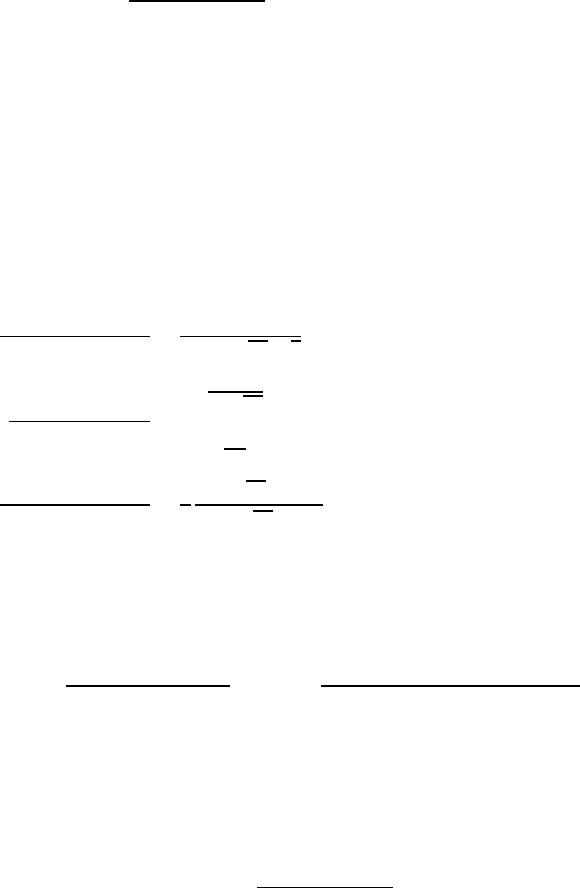
518 VIII Steady Generalized Oseen Flow in Exterior Domains
Γ
0
(ξ; R) ≤
2
|ξ|(1 + 2Rs(ξ))
,
Γ
1
(ξ; R) ≤ C
(
R
1/2
|ξ|
−3/2
(1 + 2Rs(ξ))
−3/2
, if |ξ| ≥ β/R,
|ξ|
−2
, if |ξ| ∈ (0, β/R) ,
Γ
2
(ξ; R) ≤ C
(
R|ξ|
−2
(1 + 2Rs(ξ))
−2
, if |ξ| ≥ β/R,
|ξ|
−3
, if |ξ| ∈ (0, β/R) ,
(VIII.3.12)
where C = C(β).
Proof. We begin by recalling the following noteworthy formulas (see, e.g.,
Gradshteyn & Ryzhik 1980, §§3.241, 3.249, 3 .252):
Z
∞
0
dx
(ax
2
+ bx + c)
3/2
=
2
(b + 2
√
ac)
√
c
, if a ≥ 0, b, c > 0 ,
Z
∞
0
dx
(a x
2
+ b x + c)
2
=
π
4c
√
ac
, if b = 0, a, c > 0 ,
1
b c
, if a = 0, b, c > 0 ,
Z
∞
0
dx
(ax
2
+ bx + c)
5/2
=
4
3
4
√
ac + b
c
3/2
(
√
ac + b)
2
, if a ≥ 0, b, c > 0 .
(VIII.3.13)
The inequalities in part (i) are an immediate consequence of the estimates
given in Lemma VIII.3.2 and o f (VIII.3.13 ) evaluated for a = 0, b = 1 and
c = |ξ|
2
. In order to prove part (ii), we notice that i n view of the estimates
given in Lemma VIII.3 .2, i t is enough to show that the integral
I(ξ, θ) ≡
Z
∞
0
1
(τ + |ξ + τ Re
1
|
2
)
θ
dτ =
Z
∞
0
1
(R
2
τ
2
+ (1 + 2Rξ
1
)τ + |ξ|
2
)
θ
dτ ,
for θ = 3/2, 2, 5/2 , can be increased by the right-hand side of (VIII.3.12)
1
if
θ = 3/2, and by that o f (VIII. 3.12)
2
if θ = 2, for the specified values of |ξ|.
To this end, we observe that I(ξ, θ) is convergent for the values of θ we are
considering, provided ξ 6= 0. Now, f or θ = 3/2, by a direct cal culation that
uses (VIII.3.13)
1
with a = R
2
, b = 1 + 2Rξ
1
, and c = |ξ|
2
, we get
I(ξ, 3/2) =
2
|ξ|(1 + 2Rs(ξ))
,
for all ξ 6= 0, which proves the first inequality in (VIII.3.12). Consider next
the cases θ = 2, 5/2. For all |ξ| < β/R, we have
τ + |ξ + τ Re
1
|
2
≥ (1 − 2β)τ + |ξ|
2
(VIII.3.14)
and therefore by (VIII.3.13)
2,3
with a = 0, b = (1 − 2β), and c = |ξ|
2
,

VIII.3 Fundamental Solution to the Time-Dependent Oseen Problem 519
I(ξ, θ) ≤
Z
∞
0
1
((1 −2β)τ + |ξ|
2
)
θ
dτ =
c
θ,β
|ξ|
2(θ−1)
for all ξ 6= 0 ,
which proves the second pa rt of the second and third inequalities in (VIII.3.12).
It remains to discuss the case |ξ| ≥ β/R. We consider separately the cases (a)
1 + 2 Rξ
1
≥ 0 and (b) 1 + 2Rξ
1
< 0. In case (a ), we have τ + |ξ + τRe
1
|
2
≥
R
2
τ
2
+ |ξ|
2
for all τ ≥ 0, and consequently from (VIII.3.13)
2,3
with b = 0,
a = R
2
, and c = |ξ|
2
, we have
I(ξ, θ) ≤
Z
∞
0
1
(R
2
τ
2
+ |ξ|
2
)
θ
dτ =
C
θ
R|ξ|
2θ−1
for all ξ 6= 0.
We next observe that |ξ| ≥ β/R implies
1 + 2R s(ξ) ≤ 1 + 4R|ξ| ≤
(1 + 4β)R
β
|ξ|,
from which it follows that
I(ξ, θ) ≤ C
θ,β
R
θ−3/2
(1 + 2R s(ξ))
θ−1/2
|ξ|
θ−1/2
.
In case (b), since
4R
2
|ξ|
2
− (1 + 2Rξ
1
)
2
= (2R|ξ| − 2Rξ
1
−1)(2R| ξ|+ 2Rξ
1
+ 1)
= (2R s(ξ) + 1 )(2R|ξ| − (2Rξ
1
+ 1)) > 0,
we obtain
I(ξ, θ) =
Z
∞
0
dξ
(|ξ|
2
+ (1 + 2Rx
1
)τ + R
2
τ
2
)
θ
=
Z
∞
0
dξ
(Rτ + (1 + 2Rx
1
)/2R)
2
+
4R
2
|ξ|
2
−(1 + 2Rξ
1
)
2
/(2R)
2
θ
≤
1
R
Z
∞
0
dr
r
2
+ (2R s(ξ) + 1)(2R|ξ|− (2Rξ
1
+ 1))/(2R)
2
θ
≤
1
R
Z
∞
0
dr
r
2
+ (Rs(ξ) + 1)|ξ|/(2R)
θ
≤ c
θ
R
θ−3/2
(1 + 2R s(ξ))
θ−1/2
|ξ|
θ−1/2
.
The proo f of the lemma is complete. ut
Remark VI II.3.1 The reader might have recognized that the estimates
proved in Lemma VIII.3 .3 are of the same type as those furnished for the
Stokes f unda mental solution U (ξ) in (IV.2.3), in the case R = 0, and for
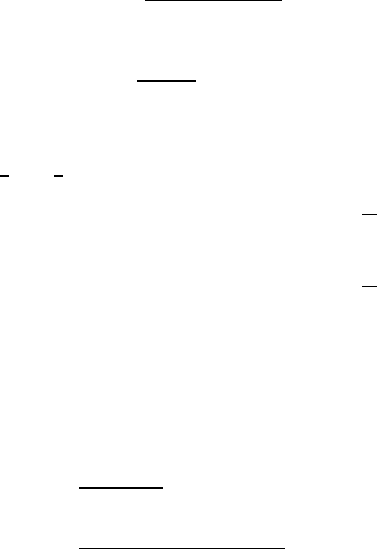
520 VIII Steady Generalized Oseen Flow in Exterior Domains
the (steady-state) Oseen fundamental solution, E(ξ; R/2), i n (VII.3.23 ) and
(VII.3.3 1), in the case R > 0. These properties–which are at the foundation
of our approach to the study of the asymptotic behavior of weak solutions to
(VIII.0.7), (VIII.0.2)–are not surprising, in that they can be expected from
the fact that for all ξ ∈ R
3
−{0},
lim
t→∞
Z
t
0
Γ (ξ, τ)dτ = U (ξ) ,
lim
t→∞
Z
t
0
Γ (ξ, τ; R)dτ = E(ξ; R/2) ;
see Thomann & Guenther (20 06), Deuring, Kraˇcmar, & Neˇcasov´a (2009) .
Exercise VIII.3.1 (Generalization of Lemma VIII.3.3(i)) Let α be a multi-index,
and set
Γ
α
(ξ) =
Z
∞
0
|D
α
Γ (ξ, t; 0)|dt .
Employing the pointwise inequality (Solonnikov 1964; Corollary in §5)
|D
α
ξ
Γ (ξ, t; 0)| ≤
C
(t + |ξ|
2
)
(|α|+3)/2
, |α| = 0, 1, 2, . . . ,
show that
Γ
α
(ξ) ≤
C
α
|ξ|
|α|+1
, for all ξ ∈ R
3
− {0}.
Exercise VIII.3.2 (Mizumachi, 1984, Lemma 3) Prove the following inequalities.
Let 1 ≤ q
1
<
3
2
and
3
2
< q
2
. Then
Z
∞
0
Z
R
3
∩{x
2
2
+x
2
3
<1}
(t + |x + te
1
|
2
)
−2q
1
dx
!
1
q
1
dt < ∞,
Z
∞
0
Z
R
3
∩{x
2
2
+x
2
3
≥1}
(t + |x + te
1
|
2
)
−2q
2
dx
!
1
q
2
dt < ∞.
Hint: Use polar coordinates with respect to (x
2
, x
3
) .
Our next task is to give po intwise estimates for the following convolution
integrals:
K(x) =
Z
R
3
Γ
1
(x − y)
(1 + |y|)
2
dy ,
J(x; R) =
Z
R
3
Γ
1
(x − y; R)
(1 + |y|)
2
(1 + 2Rs(y))
2
dy , R > 0 .
(VIII.3.15)
For K, we have the fo llowing result, of simpl e proof.

VIII.3 Fundamental Solution to the Time-Dependent Oseen Problem 521
Lemma VIII.3.4 There exi sts a constant C
1
> 0 such that
K(x) ≤
C
1
1 + |x|
. (VIII.3.16)
Proof. By Lemma VIII.3.3(i), we have
K(x) ≤ c
Z
R
3
1
|x − y|
2
(1 + |y|)
2
dy ,
and so, by Lemma II.9.2, it follows that
K(x) ≤ c|x|
−1
, for all x ∈ R
3
−{0}. (VIII.3.17)
Furthermore, by the H¨older inequality with exponent q ∈ (3/2, 3), we obtain
K(x) ≤ c
1
Z
|x−y|≤1
|x − y|
−2
dy
+c
2
Z
R
3
(1 + |x − y|)
−2q
0
dy
1/q
0
Z
R
3
(1 + |y|)
−2q
dy
1/q
≤ c
3
.
(VIII.3.18)
The proof of (VIII. 3.16) then follows from (VIII.3.17) and (VIII.3.18). The
lemma i s completely proved.
ut
In order to evaluate the other convolution in (VIII.3.15), we need the
following lemma, which is a particular case of a more general result due to
Farwig (1992b, Lemma 3.1), a nd to which we refer the reader for the proof
(see also Kraˇcmar, Novotn´y, & Pokorn´y 2001, Theorem 3.2).
Lemma VIII.3.5 Let
G(x) =
Z
R
3
η
1
(y)η
2
(x − y) dy ,
where η
1
satisfies at least one of the conditions
η
1
(y) ≤
(
c
1
(1 + |y|)
−3/2
(1 + 2s(y))
−3/2
if |y| ≥ c
0
,
c
2
|y|
−2
if |y| ≤ c
0
,
(A)
η
1
(y) ≤ c
3
(1 + |y|)
−3/2
(1 + 2s(y))
−3/2
, for all y ∈ R
3
, (B)
whereas η
2
satisfies
η
2
(y) ≤ c
4
(1 + |y|)
−2
(1 + 2s(y))
−2
, for all y ∈ R
3
,

522 VIII Steady Generalized Oseen Flow in Exterior Domains
for some (positive) constants c
i
, i = 0, . . ., 4. In case (B), this assumption may
be weakened to the following one:
η
2
(y) ≤
(
c
5
(1 + |y|)
−2
(1 + 2s(y))
−2
if |y| ≥ c
6
,
c
7
|y|
−2
if |y| ≤ c
6
,
for som e c
5
, c
6
, c
7
> 0. Then, there i s C > 0 such that
3
G(x) ≤
C
(1 + |x|)(1 + 2s(x))
.
The previo us lemma allows us to prove the following one.
Lemma VIII.3.6 Let K = max{1, R}. There exists a constant C > 0, de-
pending onl y on β, such that
J(x; R) ≤
K C
(1 + |x|)(1 + 2Rs(x))
. (VIII.3.19)
Proof. The only difficulty of the proof consists in a careful eva luation of the
dependence on the Reynolds number R of the constant entering the numerator
of the fraction in the i nequality (VIII. 3.19). For a given x ∈ R
3
, we consider
the following partition of R
3
:
R
3
= {y ∈ R
3
: |x − y| ≤ β/R} ∪ {y ∈ R
3
: |x − y| > β/R}.
From (VIII.3.12 ) and (VIII.3.15)
2
, we thus have, accordingl y,
J(x; R) ≤ C(β)
Z
R|x−y|≤β
|x −y|
−2
(1 + |y|)
−2
(1 + 2Rs(y))
−2
dy
+R
1
2
Z
R|x−y|>β
[|x − y|(1 + 2Rs(x −y))]
−
3
2
(1 + |y|)
−2
(1 + 2Rs(y))
−2
dy
≡ C(β) (J
1
(x) + J
2
(x)) .
(VIII.3.20)
We begin by estimating the function J
2
(x). With the substitution ξ = Ry,
we obtain
J
2
(x) =
1
R
Z
|Rx−ξ|>β
[|Rx−ξ|(1+2s(Rx−ξ))]
−
3
2
(1+|ξ|/R)
−2
(1+2s(ξ))
−2
dξ ,
(VIII.3.21)
3
Actually, as shown by Farwig (1992b), under t he given assumption, the function
G possesses a better decay rate than that stated here. However, this improvement
will not be necessary to our purposes. For related inequalities, see also Lemma
XI.6.2

VIII.3 Fundamental Solution to the Time-Dependent Oseen Problem 523
and so
J
2
(x) =
1
R
Z
{|Rx−ξ|>β}∩{|ξ|<1}
j(x, y)dy +
1
R
Z
{|Rx−ξ|>β}∩{|ξ|≥1}
j(x, y)dy
≡ J
(1)
2
(x) + J
(2)
2
(x) ,
(VIII.3.22)
where j(x, y) denotes the integrand function in (VIII .3. 21). Observing that
ξ ∈ {ζ ∈ R
3
: |Rx − ζ| ≥ β} =⇒
1
|Rx − ξ|
≥
4
1 + |Rx − ξ|
, (VIII.3.23)
we obtain
J
(1)
2
(x) ≤ R
Z
|ξ|<1
[(1 + |Rx − ξ|)(1 + 2s(Rx − ξ))]
−
3
2
|ξ|
−2
(1 + 2s(ξ))
−2
dξ
= R
Z
R
3
[(1 + |Rx − ξ|)(1 + 2s(Rx − ξ))]
−
3
2
η(ξ)dξ ,
where
η(z) =
(
|z|
−2
if |z| < 1 ,
0 if |z| ≥ 1 .
(VIII.3.24)
From Lemma VIII.3.5 we thus obtain
J
(1)
2
(x) ≤ c
R
(1 + R|x|)(1 + 2Rs(x))
≤
c K
(1 + |x|)(1 + 2Rs(x))
, (VIII. 3.25)
where we have used the elementary inequality
t
1 + t a
≤
max {1, t}
1 + a
, t, a ≥ 0 . (VIII.3.26)
In a similar fashion, again by (VIII.3.23) and by Lemma VIII.3.5,
J
(2)
2
(x) ≤ R
Z
|ξ|≥1
[(1+|Rx − ξ|)(1+ 2s(Rx − ξ))]
−
3
2
[(1 + |ξ|)(1 + 2s(ξ))]
−2
dξ
≤ R
Z
R
3
[(1 + |Rx − ξ|)(1 + 2s(Rx − ξ))]
−
3
2
[(1 + |ξ|)(1 + 2s(ξ))]
−2
dξ
≤
c K
(1 + |x|)(1 + 2Rs(x))
.
From this latter relation and from (VIII.3.21)–(VIII.3.25), we conclude that
J
2
(x) ≤
c K
(1 + |x|)(1 + 2 Rs(x))
. (VIII.3.27)
In order to estima te J
1
(x) we distinguish the following cases: (a) |x| ≤ β/R,
and (b) |x| > β/R. In case (a), from the obvious inequality
524 VIII Steady Generalized Oseen Flow in Exterior Domains
1
1 + 4β
≤
1
1 + 2 Rs(x)
≤ 1 for all x ∈ B
β/R
,
and from Lemma II. 9.2 and (VIII.3.18), we obtain
J
1
(x) ≤
Z
R
3
|x − y|
−2
(1 + |y|)
−2
dy ≤
c
1
1 + |x|
≤
c
2
(β)
(1 + |x|)(1 + 2Rs(x))
, for |x| ≤ β/R.
(VIII.3.28)
We next assume |x| > β/R. From (VIII.3.20), we have
J
1
(x) ≤ C(β)
Z
R|x−y|≤
β
2
|x −y|
−2
(1 + |y|)
−2
(1 + 2Rs(y))
−2
dy
+
Z
β
2
<R|x−y|≤β
|x −y|
−2
(1 + |y|)
−2
(1 + 2Rs(y))
−2
dy
≡ C(β) (J
3
(x) + J
4
(x)) .
(VIII.3.29)
With the change of variable ξ = Ry, we obtain
J
3
(x) =
1
R
Z
|Rx−ξ|≤
β
2
|Rx − ξ|
−2
(1 + |ξ|/R)
−2
(1 + 2 s(ξ))
−2
dξ
≤ R
Z
|Rx−ξ|≤
β
2
|Rx − ξ|
−2
|ξ|
−2
(1 + 2 s(ξ))
−2
dξ .
Since R|x| > β, we have, by the triangle i nequality,
|ξ| ≥ R|x| − |Rx −ξ| > β − β/2 = β/2 ,
for a ll ξ such that |Rx −ξ| ≤ β/2. Therefore,
J
3
(x) ≤ c(β)R
Z
|Rx−ξ|≤
β
2
|Rx − ξ|
−2
(1 + |ξ|)
−2
(1 + 2 s(ξ))
−2
dξ
= c(β)R
Z
R
3
η(ξ)(1 + |Rx − ξ|)
−2
(1 + 2 s(Rx − ξ))
−2
dξ ,
where the function η is defined in (VIII.3.24). As a consequence, from Lemma
VIII.3.5 and (VIII.3.26) we deduce
J
3
(x) ≤
c K
(1 + |x|)(1 + 2 Rs(x))
. (VIII.3.30)
Concerning J
4
(x), we obtain
J
4
(x) =
1
R
Z
β
2
<|Rx−ξ|≤β
|Rx − ξ|
−2
(1 + |ξ|/R)
−2
(1 + 2 s(ξ))
−2
dξ
≤ R
Z
β
2
<|Rx−ξ|≤β
|Rx − ξ|
−2
|ξ|
−2
(1 + 2 s(ξ))
−2
dξ ,
(VIII.3.31)

VIII.3 Fundamental Solution to the Time-Dependent Oseen Problem 525
which implies
J
4
(x) ≤ R
Z
{
β
2
<|Rx−ξ|≤β}∩{|ξ|<1}
e
j(x, ξ)dξ
+R
Z
{
β
2
<|Rx−ξ|≤β}∩{|ξ|≥1}
e
j(x, ξ)dξ
≡ J
(1)
4
(x) + J
(2)
4
(x) ,
(VIII.3.32)
where
e
j =
e
j(x, ξ) is the integrand function in the last integral in (VIII.3.31).
We observe that obviously,
1
|Rx − ξ|
2
≤
c(β)
(1 + |Rx − ξ|)
3/2
(1 + 2s(Rx − ξ))
3/2
,
for all ξ such that
β
2
< |Rx − ξ| ≤ β .
(VIII.3.33)
Consequently,
J
(1)
4
(x) ≤ R
Z
R
3
[(1 + |Rx − ξ|)(1 + 2s(Rx − ξ))]
−3/2
η(ξ)dξ ,
where η is defined in (VIII.3.24). So, from Lemm a VIII.3.5 and (VIII.3.26) we
obtain
J
(1)
4
(x) ≤
c K
(1 + |x|)(1 + 2Rs(x))
. (VIII.3.34)
Likewise, using (VIII.3.33), we obtain
J
(2)
4
(x) ≤ R
Z
R
3
[(1 + |Rx −ξ|)(1 + 2 s(Rx −ξ))]
−3/2
[(1 + |ξ|)(1 + 2 s(ξ))]
−2
dξ ,
and again by Lemma VIII.3.5 and (VIII.3.26), we obtain
J
(2)
4
(x) ≤
c K
(1 + |x|)(1 + 2Rs(x))
. (VIII.3.35)
By collecting (VIII.3.29)–(VIII.3.32), and (VIII.3.34), (VI II.3.35), we deduce
J
1
(x) ≤
c K
(1 + |x|)(1 + 2Rs(x))
, |x| > β/R. (VIII.3.36)
Inequality (VII I.3.19) follows from (VIII.3. 20), (VIII.3.27), (VIII.3.29), and
(VIII.3.36), and the proof of the lemma is compl ete.
ut
