Гаджинский А.М. Логистика

Подождите немного. Документ загружается.

Таблица 2(j

Алгоритм выбора оптимального варианта складской подсистемы

логистической системы

Определение стратегических целей логистической системы

_______________________________и

__________________

Расчет прогнозируемой величины материального потока,

проходящего через систему

________________________________и________________________________■

Составление прогноза необходимой величины запасов по системе

в целом и на отдельных участках материалопроводящей цепи

____________________________и

___________________________

Изучение транспортной сети региона обслуживания, составление схемы

материальных потоков в пределах системы распределения

________________________________и________________________________

Разработка различных вариантов построения логистической системы:

♦ с одним или несколькими складами;

♦ со складами, расположенными на тех или иных участках логистической

цепи;

♦ со складами, реализующими те или иные функции;

♦ с собственными и наемными складами.

________________________________и________________________________

Оценка логистических издержек для каждого из вариантов

________________________________а________________________________

______

Выбор для реализации одного из разработанных вариантов

______

К — полные капитальные вложения в строительство и

оборудование складов, приведенные по фактору времени —

по норме дисконта;

Т — срок окупаемости варианта.

Для реализации принимается тот вариант логистичес

кой системы, который обеспечивает минимальное значение

приведенных (годовых) затрат.

В процессе проектирования логистических систем на

базе информации о схеме потоков и о планируемых запа

сах определяется оптимальное количество и мощность скла

дов, разрабатывается их рациональная дислокация в реги

оне контролируемого потока.

400

22.2. Определение оптимального количества

складов в зоне обслуживания

Решения по развитию складской сети необходимо при

нимать на основе анализа полной стоимости, что означа

ет учет всех экономических изменений, возникающих при

изменении количества складов в логистической системе.

Рассмотрим модель системы распределения материаль

ного потока, представленную на рис. 110. Допустим, что пред-

приятие-поставщик, обслуживает сеть оптовых покупателей,

расположенных на определенной территории. Количество

•ъ/

а) б) в)

Условные обозначения:

■ - распределительные центры (склады);

• - потребители материального потока;

_ - материальные потоки.

Рис. 110. Варианты организации распределения

материального потока:

а) с одним распределительным центром;

б) с двумя распределительными центрами;

в) с шестью распределительными центрами

401

покупателей и объемы потребляемых ими потоков в рамках

данной задачи являются величинами постоянными.

На рисунке представлено три варианта организации

распределения: с помощью одного, двух или шести складов

(соответственно рисунки а, б и в). Очевидно, что в случае

принятия варианта (а) транспортные расходы по доставке

будут наибольшими. Вариант (в) предполагает наличие ше

сти распределительных центров, максимально приближен

ных к местам сосредоточения потребителей материального

потока. В этом случае транспортные расходы по товаро-

снабжению будут минимальными. Однако появление в сис

теме распределения пяти дополнительных складов увели

чивает эксплуатационные расходы, затраты на доставку

товаров на склады, затраты на управление всей распреде

лительной системой. Не исключено, что дополнительные

затраты в этом случае могут значительно превысить эко

номический выигрыш, полученный от сокращения пробега

транспорта, доставляющего товары потребителям.

В табл. 26 приведены условные зависимости отдельных

видов издержек, связанных с функционированием системы

распределения, от количества входящих в эту систему скла

дов. Как видим, при изменении количества складов в систе

ме распределения часть издержек, связанных с процессом

доведения материального потока до потребителя, возраста

ет, а часть снижается. В нашем условном примере предпоч

тительнее оказался вариант б, согласно которому район об

служивается двумя складами. В этом случае суммарные зат

раты являются минимальными (1445 тыс. рублей в месяц).

Как видим, при изменении количества складов в систе

ме распределения часть издержек, связанных с процессом

доведения материального потока до потребителя, возрас

тает, а часть снижается. Это позволяет ставить и решать

задачу поиска оптимального количества складов. Рассмот

рим графический метод решения данной задачи.

Выберем в качестве независимой переменной величину

N — количество складов, через которые осуществляется

402

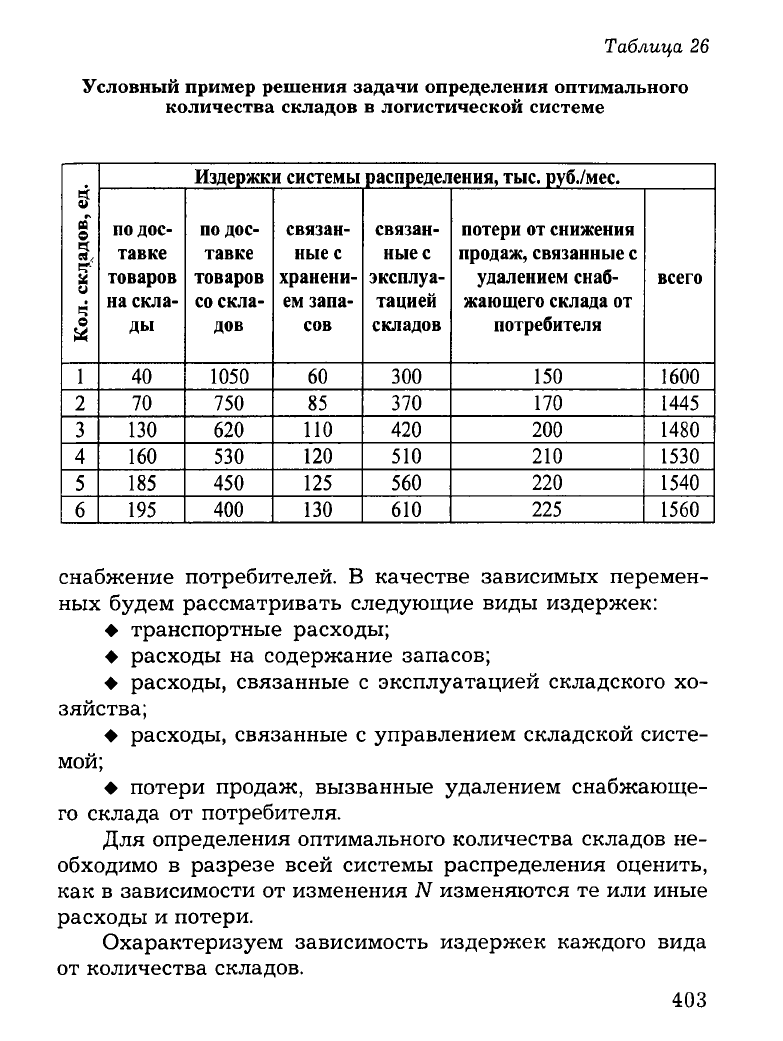
Таблица 26

Условный пример решения задачи определения оптимального

количества складов в логистической системе

Издержки системы

распределения, тыс. руб./мес.

по дос

тавке

товаров

на скла

ды

по дос

тавке

товаров

со скла

дов

связан

ные с

хранени

ем запа

сов

связан

ные с

эксплуа

тацией

складов

потери от снижения

продаж, связанные с

удалением снаб

жающего склада от

потребителя

всего

1 40

1050

60 300 150

1600

2 70 750 85 370 170 1445

3 130 620

НО

420 200 1480

4 160 530

120 510 210 1530

5 185

450 125 560

220

1540

6 195

400 130 610 225 1560

снабжение потребителей. В качестве зависимых перемен

ных будем рассматривать следующие виды издержек:

♦ транспортные расходы;

♦ расходы на содержание запасов;

♦ расходы, связанные с эксплуатацией складского хо

зяйства;

♦ расходы, связанные с управлением складской систе

мой;

♦ потери продаж, вызванные удалением снабжающе

го склада от потребителя.

Для определения оптимального количества складов не

обходимо в разрезе всей системы распределения оценить,

как в зависимости от изменения N изменяются те или иные

расходы и потери.

Охарактеризуем зависимость издержек каждого вида

от количества складов.

403

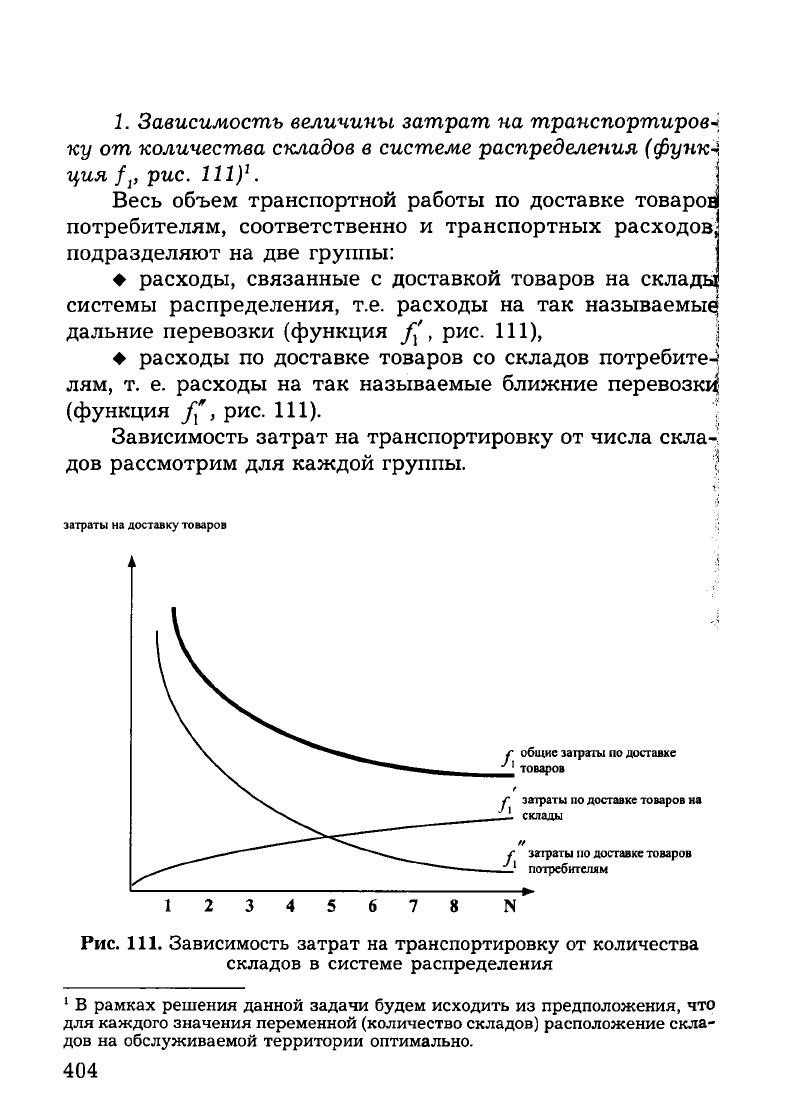
1. Зависимость величины затрат на транспортиров4

ку от количества складов в системе распределения (функА

ция fj, рис. I ll)1. |

Весь объем транспортной работы по доставке товароа

потребителям, соответственно и транспортных расходов!

подразделяют на две группы: |

♦ расходы, связанные с доставкой товаров на складь|

системы распределения, т.е. расходы на так называемы^

дальние перевозки (функция f[, рис. 111),

♦ расходы по доставке товаров со складов потребите-1

лям, т. е. расходы на так называемые ближние перевозку

(функция f", рис. 111). |

Зависимость затрат на транспортировку от числа скла

дов рассмотрим для каждой группы. |

затраты на доставку товаров

Рис. 111. Зависимость затрат на транспортировку от количества

складов в системе распределения

1 В рамках решения данной задачи будем исходить из предположения, что

для каждого значения переменной (количество складов) расположение скла

дов на обслуживаемой территории оптимально.

404

При увеличении количества складов в системе распре

деления стоимость доставки товаров на склады возрастает,

так как увеличивается количество поездок, а также сово

купная величина пробега транспорта. Характер зависимос

ти не прямолинейный, так как здесь имеются условно-по-

стоянная и условно-переменная составляющие, в результа

те чего расходы по доставке растут медленнее, чем рас

стояние.

Другая часть транспортных расходов — стоимость дос

тавки товаров со складов потребителям — с увеличением

количества складов снижается. Это происходит в результа

те резкого сокращения пробега транспорта.

Суммарные транспортные расходы (функция / , рис. 111)

при увеличении количества складов в системе распределе

ния, как правило, убывают.

2. Зависимость затрат на содержание запасов от коли

чества складов в системе распределения (функция /2 рис. 112).

Увеличение количества складов в системе распределе

ния влечет за собой сокращение зоны обслуживания от

дельного склада, а следовательно, и размера запаса на от

дельном складе. Однако запас на отдельном складе сокра

щается не столь быстро, как зона обслуживания, в резуль

тате суммарный запас в распределительной системе возра

стает.

Первая причина — необходимость содержания страхо

вого запаса. В модели с несколькими складами страховой

запас в общем случае необходимо создавать на каждом скла

де. Сокращение складской сети влечет за собой концентра

цию страхового запаса и общее снижение потребности в

нем. Ожидаемую экономию рассчитывают с помощью зако

на квадратного корня, согласно которому размер стра

хового запаса, а следовательно, и сумма издержек по его

содержанию возрастают пропорционально корню квадрат

ному из числа складов1.

1 Закон квадратного корня подробно рассмотрен в § 20.2.

405

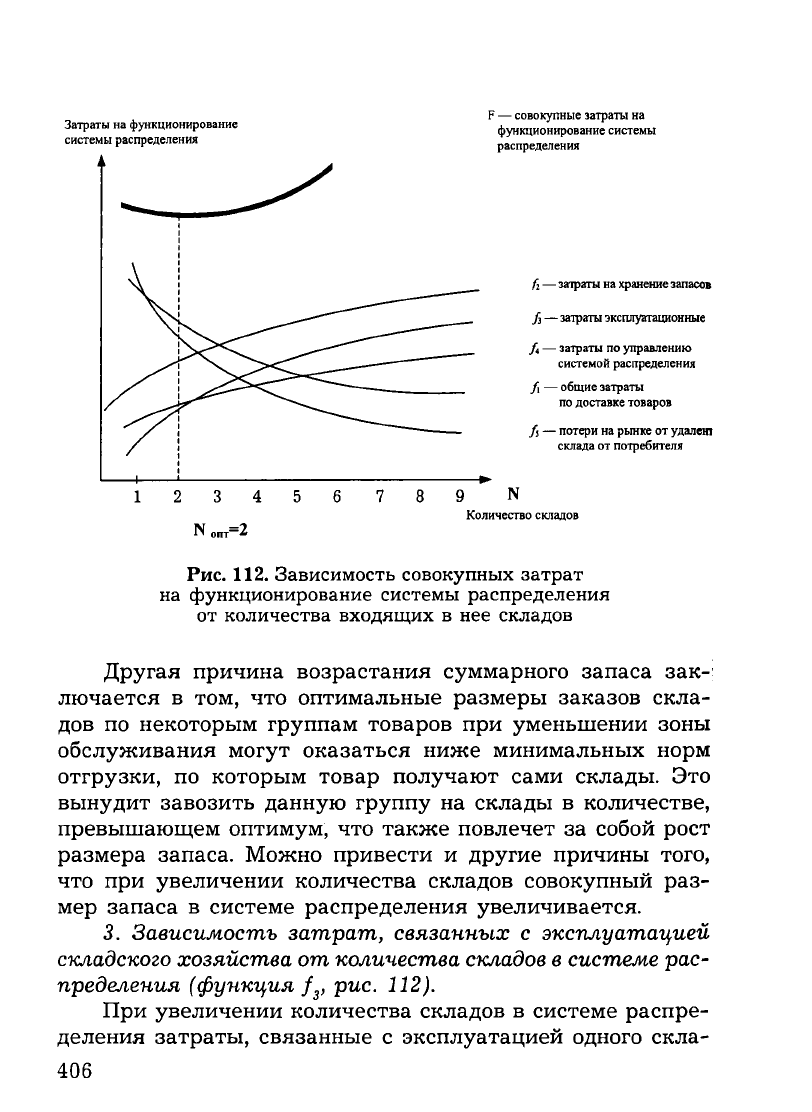
Затраты на функционирование

системы распределения

F — совокупные затраты на

функционирование системы

распределения

fi — затраты на хранение запасов

fi — затраты эксплуатационные

fA — затраты по управлению

системой распределения

/1 — общие затраты

по доставке товаров

fi — потери на рынке от удален!

склада от потребителя

N .nT=2

Количество складов

Рис. 112. Зависимость совокупных затрат

на функционирование системы распределения

от количества входящих в нее складов

Другая причина возрастания суммарного запаса зак

лючается в том, что оптимальные размеры заказов скла

дов по некоторым группам товаров при уменьшении зоны

обслуживания могут оказаться ниже минимальных норм

отгрузки, по которым товар получают сами склады. Это

вынудит завозить данную группу на склады в количестве,

превышающем оптимум, что также повлечет за собой рост

размера запаса. Можно привести и другие причины того,

что при увеличении количества складов совокупный раз

мер запаса в системе распределения увеличивается.

3. Зависимость затрат, связанных с эксплуатацией

складского хозяйства от количества складов в системе 'рас

пределения (функция f3, рис. 112).

При увеличении количества складов в системе распре

деления затраты, связанные с эксплуатацией одного скла

406

да, снижаются. Однако совокупные затраты распредели

тельной системы на содержание всего складского хозяй

ства возрастают. Происходит это в связи с так называемым

эффектом масштаба: при уменьшении площади склада, эк

сплуатационные затраты, приходящиеся на 1 м2, увеличи

ваются. Например, в торговле при уменьшении площади

склада с 10,5 тыс. м2 до 1,5 тыс. м2, т. е. в 7 раз, эксплуатаци

онные затраты уменьшаются всего лишь в 5,25 раза. Заме

на одного склада семью (общая площадь остается той же —

10,5 тыс. м2) в этом случае повлечет за собой увеличение

эксплуатационных расходов в 1,4 раза.

Примерная зависимость величины удельных эксплуа

тационных расходов от размера склада (сфера торговли то

варами народного потребления) приведена в табл. 27.

Таблица 27

Примерная зависимость эксплуатационных затрат,

в расчете на 1 м2 площади склада от размера

складской площади

Складская

площадь, м2

Структура удельных эксплуатаци

онных затрат (удельные эксплуа

тационные затраты склада площа

дью 1500 м2 приняты за единицу)

Эксплуатационные

затраты, в расчете

на 1 м2 склада, уде

1500

1 60

3000 0,88 53

5750 0,82

10500 0,75

13000 0,65 39

4. Зависимость затрат, связанных с управлением рас

пределительной системой от количества входящих в нее

складов (функция f4 рис. 112).

Характер данной зависимости представлен кривой / .

Здесь также действует эффект масштаба, в связи с чем

407

при увеличении количества складов кривая расходов на си

стемы управления делается более пологой.

5. Зависимость потерь продаж, вызванных сокраще

нием числа складов и соответствующим удалением снаб

жающего склада от потребителя, от количества складов

в системе распределения (функция f5, рис. 112).

При сокращении количества складов среднее расстоя

ние до обслуживаемых пунктов возрастает. Становится

сложнее поддерживать сервис на прежнем уровне. Слож

нее поставлять грузы по системе “точно в срок”, так как

возросшие расходы на транспортировку увеличивают эко

номически оптимальный размер отгружаемой партии.

Кроме того, потребителю сложнее самому приехать на

склад и выбрать ассортимент. Могут возникнуть задержки в

пути следования груза. Действуют и другие негативные

факторы, снижающие заинтересованность потребителя в

более дальнем поставщике. Недаром маркетологи, рекла

мируя сбытовое предприятие, выделяют фразу: “наш склад

рядом с вами”.

Сокращение складов в зоне обслуживания может при

вести также и к росту транспортно-заготовительных затрат

клиента склада, так как доставка со склада, как правило,

осуществляется по более низким тарифам, чем доставка

на склад. Размещая склад вдали от клиента, предприятие

тем самым вынуждено продвигать товар в зону обслужива

ния по более высоким транспортным тарифам, что неиз

бежно сказывается на конечной цене товара, а следова

тельно, и на объемах реализации.

Зависимость совокупных затрат на функционирование

системы распределения от количества входящих в нее скла

дов (функция F) получают путем сложения всех, приведен

ных на рис. 112 графиков. Абсцисса минимума кривой сово

купных затрат даст оптимальное значение количества скла

дов в системе распределения (в нашем случае — 2 склада).

Допустим, что упомянутое предприятие-поставщик

имеет на территории обслуживания шесть складов. Переход

408

к системе обслуживания с помощью двух складов сопро

вождается увеличением одних издержек и сокращением

других. Общий же размер издержек уменьшается (рис. 113).

В завершение следует отметить, что в последние годы

в странах западной Европы наблюдается тенденция сокра

щения количества складов, особенно в розничной торговле.

При этом, несмотря на рост транспортных расходов, в це

лом по системе распределения наблюдается экономия

средств, особенно за счет сокращения страховых запасов.

Однако механически переносить закономерности, действу

ющие в странах с развитой рыночной экономикой, на Рос

сийскую Федерацию нельзя. В настоящее время в отече

ственной торговле пока еще нет той конкуренции, которая

имеет место в Западной Европе и требует там поддержа

ния высокого уровня страховых запасов. Российские пред

приятия могут позволить себе обеспечивать, покупателю

Полная стоимость распределения Полная стоимость распределения

при 6 складах при 2 складах

Рис. 113. Общее снижение затрат, полученное в результате

анализа полной стоимости распределния

409