Frank A., Jolie J., Van Isacker P. Symmetries in Atomic Nuclei: From Isospin to Supersymmetry

Подождите немного. Документ загружается.

80 3 Supersymmetry in Nuclear Physics

symmetry or vice versa. This point, as well as its signiﬁcance in the analysis

of data, is explained in the ﬁnal section of this chapter.

3.1 The Interacting Boson–Fermion Model

As mentioned in the introduction to this chapter, the IBFM can be thought

of, on one level, as a core–particle coupling model with the advantage of a

versatile IBM description of the collective core states. However, there are two

aspects of the approach which go further. First, as for the IBM in even–even

nuclei, it is possible to forge a link between the collective hamiltonian and the

underlying single-particle shell structure. Second, symmetries play a central

role in the IBFM, just as they do in the boson case. The three symmetries

which emerge from the algebraic treatment of the boson problem reappear in

the odd-mass formalism although their existence and structure now depend

on the single-particle space available to the odd fermion.

The IBFM of odd-mass nuclei was introduced by Iachello and Scholten

[162]. Diﬀerent versions of the model can be constructed depending on the

realization of the algebra in terms of creation and annihilation operators.

One such realization, called Holstein–Primakoﬀ, leads to a somewhat diﬀerent

version of the IBFM, which is known as the truncated quadrupole phonon–

fermion model [163]. The discussion here shall be limited to a brief outline

of the basic features of the simplest version of the IBFM.

The basic building blocks of the IBFM are Nsand d bosons, in terms of

which the even–even core states are modeled, and fermions which occupy a

set of single-particle orbits {j, j



,...}. Low-lying collective states of an odd-

mass nucleus with 2N + 1 valence nucleons are approximated as N-boson

states coupled to a single fermion. The creation and annihilation operators

are b

†

and b

for the bosons and a

†

and a

for the fermions, and satisfy

the (anti-)commutation relations

†



} = δ



, {a

†



} = {a



} =0, (3.1)

and

†



]=δ



, [b

†



]=[b



]=0. (3.2)

Furthermore, it is assumed that boson and fermion operators commute,



]=[b

†



]=[b

†



]=[b

†



]=0. (3.3)

To the extent that nucleons are ideal fermions (which, in fact, they are not

since they consist of three quarks), the anti-commutation relations (3.1) are

valid exactly. The bosons are composite objects with an internal structure

and only approximately satisfy the commutation relations (3.2) and (3.3).

The approach followed in the IB(F)M is to impose particle statistics rigor-

ously and to correct for the neglect of the Pauli principle by including addi-

tional correlations in the hamiltonian. Such Pauli corrections are particularly

important for the boson–fermion interaction.

3.1 The Interacting Boson–Fermion Model 81

The hamiltonian of the IBFM consists of a boson and a fermion part, and

a boson–fermion interaction, and can be written as

H = H

+ H

+ V

. (3.4)

The boson hamiltonian can be taken directly from the IBM, see Sect. 2.2. As

in the boson case, the fermion hamiltonian can be expanded in the order of

the interaction. In general, for odd-mass nuclei, only one fermion is coupled

to the boson core and this implies that only the one-body part of the fermion

hamiltonian matters, which then can be written as





, (3.5)

where n

is the number of fermions in orbit j and 

its single-particle energy.

We note that the simplication of the fermion hamiltonian is a consequence

of the assumption of coupling one fermion to the bosons. If several fermions

are coupled to the core, their mutual interaction should be included in H

Notably, this is important in odd–odd nuclei where a neutron and a proton are

coupled to the even–even core, as will be discussed in Chap. 5. The need for

a fermion–fermion interaction also arises if two-particle or two-quasi-particle

states are coupled to a boson core which is required for the description of

high-spin phenomena such as band crossing and back bending [164, 165, 166].

This approach has even been extended to the coupling of four-quasi-particle

states to a boson core [167, 168]. The third term in the hamiltonian (3.4)

is the interaction between bosons and fermion which, in lowest order, is of

two-body character,



ljl



ljl





†

× a

†

)

(J)

× (



× ˜a



)

(J)



(0)

, (3.6)

where the v coeﬃcients are related to the interaction matrix elements

between normalized boson–fermion states,

lj; JM



; JM

 =



2J +1

ljl



. (3.7)

The boson–fermion interaction (3.6) is too general to be of use in a phe-

nomenological analysis. On the basis of shell-model considerations, a simplied

form of this interaction can be proposed [162] which contains a monopole, a

quadrupole and an exchange term,

monopole





†

(0)

× (a

†

× ˜a

)

(0)



(0)

quadrupole







× (a

†

× ˜a



)

(2)



(0)

exchange











†

× ˜a

)



)

× (

d × a

†



)



)



(0)

:, (3.8)

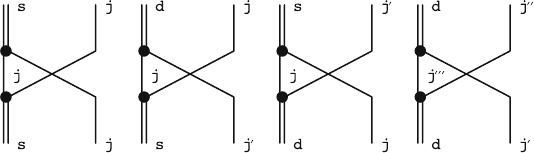
82 3 Supersymmetry in Nuclear Physics

Fig. 3.1. Schematic representation of diﬀerent boson–fermion exchange

interactions

where the notation : ···: indicates normal order and Q

is the quadrupole

operator (2.45) with an additional index B to indicate its boson character.

The monopole and quadrupole interactions are the most important compo-

nents in a multipole expansion of the interaction and should be included

as such. The exchange interaction [169, 170] takes account of the fact that

the bosons have an internal structure, and this leads to the exchange ef-

fects illustrated in Fig. 3.1. Since the bosons are fermion pairs, they are

represented by a double line, while a fermion corresponds to a single line;

the vertices denote (two-nucleon) interactions. Microscopic considerations

suggest [171] that the d-to-d exchange interaction is its most important

component.

3.2 Bose–Fermi Symmetries

The Lie algebras associated with the IBFM are U

(6) and U

(Ω) where

Ω =



(2j + 1) denotes the size of the single-particle space available to

the fermion. The usual boson algebra U

(6) describes the collective core

excitations, while U

(Ω) corresponds to the unitary transformations among

the available single-particle states a

†

|o. The dynamical algebra for an odd-

mass nucleus is then the product algebra

(6) ⊗ U

(Ω). (3.9)

It contains two sets of generators, in terms of bosons b

†



and in terms of

fermions a

†

˜a



. Note that the IBFM hamiltonian conserves the number

of bosons as well as fermions; it can be expressed in terms of the genera-

tors of the algebra (3.9) which therefore can be considered as the dynamical

algebra.

The existence of analytically solvable IBFM hamiltonians relies on iso-

morphisms between boson and fermion algebras. A simple example of two

isomorphic algebras is provided by the angular momentum algebras which

can be deﬁned for bosons and for fermions. The former consists of the angu-

lar momentum operators L

which generate the boson algebra SO

(3) and

3.2 Bose–Fermi Symmetries 83

occurs in the lattice (2.36). The fermion angular momentum operators L

have commutation properties which are identical to those of L

and thus

are generators of an identical Lie algebra which shall be denoted as SU

(2).

Although the elements of both Lie algebras can be put into one-to-one cor-

respondence, expressed by the isomorphism SO

(3)  SU

(2), the diﬀerence

in notation refers to the fact that the bosons can couple to integer angular

momenta only, while for the fermions they can also be half-integer. Because of

the property (3.3), L

and L

commute, and the summed operators L

+ L

close under commutation and generate the boson–fermion algebra SU

B+F

(2).

This is the algebra of the total angular momentum, which can be integer or

half-integer, depending on whether the number of fermions is even or odd.

Since SO

(3) is a subalgebra of U

(6) and SU

(2) is one of U

(Ω), it follows

that SU

B+F

(2) is a subalgebra of U

(6) ⊗ U

(Ω),

(6) ⊗ U

(Ω) ⊃···⊃SU

B+F

(2). (3.10)

In the following, we shall omit the superscripts B+F in the total angular

momentum algebra which then shall be denoted as SO(3), Spin(3) or SU(2),

depending on whether the angular momenta are only integer or only half-

integer or both integer and half-integer.

The classiﬁcation of all analytically solvable, rotationally invariant IBFM

hamiltonians amounts to ﬁnding the subalgebras of U

(6) ⊗ U

(Ω)which

contain SU(2). It is clear that this classiﬁcation depends on Ω and the spe-

ciﬁc single-particle orbits {j, j



,...} available to the fermion. The subalgebra

structure of U

(6) ⊗ U

(Ω) depends on the existence of isomorphisms be-

tween boson and fermion algebras: Whenever an isomorphism is established

between G

and G

, G

G

, a boson–fermion algebra G

B+F

can be de-

ﬁned (by adding the corresponding generators) and incorporated into the

lattice (3.10).

The algebraic structure of the boson part of the problem is well known and

contained in lattice (2.36), although careful consideration should be given to

the parameter symmetries mentioned in Sect. 2.2. On the fermion side, since

Ω can be large, the algebraic substructure of U

(Ω) may be complex and not

known a priori. A powerful method to determine subalgebras is based on the

separation of the nucleon angular momentum j =

l +

s into a pseudo-orbital

part

l and a pseudo-spin part

s [84]. For ˜s =1/2 this is a generalization

of the pseudo-spin scheme of Sect. 2.1. This separation carries with it the

deﬁnition of the particle creation operators

†

l˜s,jm



˜m



l ˜m

˜s ˜m

|jm

a

†

l ˜m

˜s ˜m

, (3.11)

where a

†

l ˜m

˜s ˜m

is related as follows to the usual (ls)j-coupled creation

operators:

84 3 Supersymmetry in Nuclear Physics

†

l ˜m

˜s ˜m





l ˜m

˜s ˜m

|jm

a

†

(3.12)

The separation j =

s, is equivalent to the reduction U

(Ω) ⊃ U

l+1)⊗

(2˜s + 1), where the generators of U

l + 1) are scalars in ˜s, while the

generators of U

(2˜s + 1) are scalars in

These techniques deﬁne a large class of subalgebras of U

(Ω), which sub-

sequently may be combined with U

(6) or one of its subalgebras by virtue

of isomorphism. In this way the classiﬁcation of analytically solvable IBFM

hamiltonians is reduced to a group-theoretical problem concerning the sub-

algebra structure of U

(6) ⊗U

(Ω). A comprehensive review of the dynam-

ical symmetries of IBFM, which includes results up to 1991, was given in

Ref. [161]; experimental examples were reviewed in Ref. [172]. We refer to

these reports for details on speciﬁc cases. In the next section we present the

two cases which have been most studied and which are of importance for the

subsequent discussion of supersymmetry and its extension.

3.3 Examples of Bose–Fermi Symmetries

The ﬁrst example of a dynamical-symmetry limit of the IBFM was proposed

by Iachello [37] who worked out its details in collaboration with Kuyucak [173,

174]. It concerns the case where the bosons are classiﬁed according to the

SO(6) limit of U(6) and where the fermion occupies a single orbit with j =

3/2. Accordingly, the dynamical algebra is U

(6) ⊗ U

(4) and, because of

the isomorphism SO

(6)  SU

(4), it allows the classiﬁcation

(6) ⊗ U

(4) ⊃ SO

(6) ⊗ SU

(4) ⊃ Spin

B+F

(6) ⊃

↓↓ ↓ ↓ ↓

[N] [1] σ1/2, 1/2, 1/2σ

,σ



Spin

B+F

(5) ⊃ Spin(3)

↓↓

(τ

,τ

) J

. (3.13)

Since the fundamental representation [1] of SU(4) corresponds to the repre-

sentation 1/2, 1/2, 1/2 of SO(6), the allowed labels σ

,σ

 are obtained

from the multiplication σ×1/2, 1/2, 1/2 and given by σ +1/2, 1/2, 1/2

and σ − 1/2, 1/2, −1/2, where σ takes the values known from IBM, σ =

N,N − 2,...,1 or 0. If a single fermion is coupled to the N bosons, all rep-

resentations thus obtained are labeled by half-integer numbers and these are

known as spinor representations. This is also the reason that spinor algebras

appear in the reduction (3.13). Note also that the third Spin

B+F

(6) label σ

can be either −1/2or+1/2; it can be shown that both choices are equivalent

and in the following only the absolute value |σ

| will be given. The Spin

B+F

(5)

3.3 Examples of Bose–Fermi Symmetries 85

labels (τ

,τ

) are determined from the Spin(6) ⊃ Spin(5) reduction which,

for σ

, 1/2, 1/2, is given by (τ

,τ

)=(σ

, 1/2), (σ

−1, 1/2),...,(1/2, 1/2).

Finally, the allowed values of the angular momentum J are found from

the Spin(5) ⊃ Spin(3) reduction and this gives that (τ

, 1/2) contains

J =2v+1/2, 2v−1/2,...,v+1−

[1−(−)

2(τ−v)/3

] with v = τ

,τ

−3,τ

−6,...

and v>0. This also shows that for τ

≥ 7/2 some J values may occur more

than once.

We can now follow the procedure as outlined in Sect. 1.2 and write

the hamiltonian in terms of Casimir operators of algebras in the nested

chain (3.13). If operators are omitted that give a constant contribution to

all states of a given odd-mass nucleus, this leads to a hamiltonian with four

Casimir operators,

H = κ

[SO

(6)] + κ



[Spin

B+F

(6)] + κ

[Spin

B+F

(5)]

+κ

[Spin(3)], (3.14)

with eigenvalues that are known in terms of the quantum numbers appearing

in (3.13),

E(σ, σ

,τ

,J)=κ

σ(σ +4)+κ



[σ

(σ

+4)+σ

(σ

+2)+σ

]

+κ

[τ

(τ

+3)+τ

(τ

+ 1)] + κ

J(J +1). (3.15)

Furthermore, the eigenstates of the hamiltonian (3.14) have ﬁxed wave func-

tions, that is, they are independent of the parameters κ

and can be expressed

in terms of known isoscalar factors associated with the reductions in (3.13).

This, in turn, allows the calculation of many other nuclear properties such

as electromagnetic-transition rates and moments or particle-transfer proba-

bilities, extensively discussed in Refs. [173, 174]. Empirical evidence for this

dynamical-symmetry limit of the IBFM is found in the Ir–Au region, as re-

viewed in Ref. [172].

As a second example of a dynamical-symmetry limit of the IBFM, we

consider the case with a fermion in orbits with angular momenta j =1/2,

3/2 and 5/2. This scheme was ﬁrst considered by Balantekin et al. [175]. It is

particularly attractive because, for all three boson symmetries, U(5), SU(3)

and SO(6), it is possible to construct analytically solvable limits. For this

reason, this case has been the subject of several detailed studies [176, 177].

Of special relevance is the SO(6) limit [178, 179] which has been applied

extensively in the platinum isotopes (see Sect. 3.5). For an account of the

U(5) and SU(3) limits we refer to the original papers [178, 180, 181].

The relevant dynamical algebra is U

(6) ⊗ U

(12) and an isomorphism

between the boson and the fermion algebras is established by introducing a

pseudo-spin ˜s =1/2 and the pseudo-orbital angular momenta

l =0and2for

the fermion. The classiﬁcation in the SO(6) limit then becomes

86 3 Supersymmetry in Nuclear Physics

(6) ⊗ U

(12) ⊃ U

(6) ⊗ U

(2) ⊃

↓↓↓↓↓

[N] [1] [N ] [1] [1]

B+F

(6) ⊗ SU

(2) ⊃ SO

B+F

(6) ⊗ SU

(2) ⊃

↓↓ ↓ ↓

]˜s =1/2 σ

,σ

 ˜s

B+F

(5) ⊗ SU

(2) ⊃ SO

B+F

(3) ⊗ SU

(2) ⊃ Spin(3)

↓↓↓↓↓

(τ

,τ

)˜s

L ˜sJ

. (3.16)

One obtains two classes of U(6) representations: [N

] follows from the

multiplication [N] ×[1] which gives [N +1, 0] and [N,1]. The two-rowed rep-

resentations of U

B+F

(6) reﬂect a mixed-symmetry character which is allowed

for a system consisting of two sets of distinguishable quantum objects, in this

case bosons and fermions. For [N +1, 0] the U(6) ⊃ SO(6) reduction is known

from even–even nuclei and gives σ

,σ

 = N +1, 0, N − 1, 0,...,1, 0

or 0, 0.For[N, 1] one obtains σ

,σ

 = N − 1, 0, N − 3, 0,...,1, 0

or 0, 0 and σ

,σ

 = N,1, N − 2, 1,...,2, 1 or 1, 1. The SO(5) rep-

resentations contained in σ

, 0 are (τ

,τ

)=(σ

, 0), (σ

− 1, 0),...,(0, 0)

and those contained in σ

, 1 are (τ

,τ

)=(σ

, 0), (σ

− 1, 0),...,(0, 0)

and (τ

,τ

)=(σ

, 1), (σ

− 1, 1),...,(1, 1). Also for the SO(5) ⊃ SO(3)

reduction we have two cases: (τ

, 0) contains the angular momenta

L =

2v, 2v − 2, 2v − 3,...,v with v = τ

,τ

− 3,τ

− 6,... and v ≥ 0, and (τ

, 1)

contains

L =2v +1, 2v,...,v+1+δ

vτ

with v = τ

,τ

−1,...,0. Finally, the

pseudo-spin value ˜s is coupled with

L to give the total angular momentum

J. This coupling causes the typical doublet structure with J =

L ± 1/2for

odd-mass states with

L =0.

If one neglects Casimir operators which contribute to the nuclear binding

energy only, ﬁve second-order operators remain, and the hamiltonian reads

H = κ

B+F

(6)] + κ

[SO

B+F

(6)] + κ

[SO

B+F

(5)]

+κ

[SO

B+F

(3)] + κ



[Spin(3)]. (3.17)

The energy E of the eigenstates is, then, an analytic expression in terms of

the relevant quantum numbers:

E(N

,σ

,τ

L, J)

= κ

+5)+N

+ 3)] + κ

[σ

(σ

+4)+σ

(σ

+ 2)]

+κ

[τ

(τ

+3)+τ

(τ

+ 1)] + κ

L +1)+κ



J(J +1). (3.18)

Again, the eigenstates of the hamiltonian (3.14) are independent of the pa-

rameters κ

and known in terms of isoscalar factors which enables the calcu-

lation of many nuclear properties, as discussed in Refs. [178, 179]. The appli-

cation of this dynamical-symmetry limit to the nucleus

195

Pt is presented in

detail in Sect. 3.5.

3.4 Nuclear Supersymmetry 87

3.4 Nuclear Supersymmetry

In the previous section we showed how dynamical-symmetry limits arise in the

IBFM and we illustrated them with two examples. In each of these examples

it is clear that, if the no-fermion case is considered, the odd-mass classi-

ﬁcation in IBFM reduces to one of the three IBM classiﬁcations valid for

even–even nuclei. This, in fact, is a generic property and it forms the basis

of a supersymmetric model that allows a simultaneous description of even–

even and odd-mass nuclei. Note, however, that such a uniﬁed description is

not achieved with the formalism of the previous section since the dynamical

algebra U

(6) ⊗ U

(Ω) does not contain even–even and odd-mass nuclei in

a single of its representations. The search is thus on for a larger dynamical

algebra which necessarily must be supersymmetric in nature.

Nuclear supersymmetry should not be confused with fundamental super-

symmetry which predicts the existence of supersymmetric particles, such as

the photino and the selectron, for which, up to now, no evidence has been

found. If such particles exist, however, supersymmetry must be strongly bro-

ken since large mass diﬀerences must exist among superpartners, or otherwise

they would have been already detected. Competing supersymmetry models

give rise to diverse mass predictions and are the basis for current superstring

and brane theories [36, 182]. Nuclear supersymmetry, on the other hand, is

a theory that establishes precise links among the spectroscopic properties of

certain neighboring nuclei. Even-mass nuclei are composite bosonic systems,

while odd-mass nuclei are fermionic. It is in this context that nuclear su-

persymmetry provides a theoretical framework where bosonic and fermionic

systems are treated as members of the same supermultiplet. Nuclear super-

symmetry treats the excitation spectra and transition intensities of the dif-

ferent nuclei as arising from a single hamiltonian and a single set of transition

operators. A necessary condition for such an approach to be successful is that

the energy scale for bosonic and fermionic excitations is comparable which is

indeed the case in nuclei. Nuclear supersymmetry was originally postulated

by Iachello and co-workers [37, 183] as a symmetry among pairs of nuclei.

Subsequently, it was extended to quartets of nuclei, where odd–odd nuclei

could be incorporated in a natural way, as discussed in Chapt. 5.

Building on the concepts developed in the preceding sections, we now show

that even–even and odd-mass nuclei can be treated in a uniﬁed framework

based on symmetry ideas of IBM and IBFM. Schematically, states in such

nuclei are connected by the generators

⎛

⎝

†

b 0

−−−

†

⎞

⎠

, (3.19)

where indices are omitted for simplicity. States in an even–even nucleus are

connected by the operators in the upper left-hand corner of (3.19), while

88 3 Supersymmetry in Nuclear Physics

those in odd-mass nuclei require both sets of generators. The operators (3.19)

provide a separate description of even–even and odd-mass nuclei; although the

treatment is similar in both cases, no operator exists that connects even–even

and odd-mass states.

An extension of the algebraic structure (3.19) considers in addition oper-

ators that transform a boson into a fermion or vice versa:

⎛

⎝

†

b b

†

−−−

†

b a

†

⎞

⎠

. (3.20)

This set does not any longer form a classical Lie algebra which is deﬁned in

terms of commutation relations. Instead, to deﬁne a closed algebraic struc-

ture, one needs to introduce an internal operation that corresponds to a

mixture of commutation and anti-commutation, as explained in Sect. 1.2.4.

The resulting graded or superalgebra is U(6/Ω), where 6 and Ω are the di-

mensions of the boson and fermion algebras.

By embedding U

(6)⊗U

(Ω) into a superalgebra U(6/Ω), the uniﬁcation

of the description of even–even and odd-mass nuclei is achieved. From a

mathematical point of view this can be seen from the reduction

U(6/Ω) ⊃ U

(6) ⊗ U

(Ω)

↓↓↓

[N} [N ][1

]

. (3.21)

The supersymmetric representation [N} of U(6/Ω) imposes symmetry in

the bosons and anti-symmetry in the fermions and contains the U

(6) ⊗

(Ω) representations [N] × [1

] with N = N + M [183]. Thus, a single

supersymmetric representation contains states in even–even (M = 0) as well

as odd-mass (M = 1) nuclei.

To understand better the purpose of the introduction of the supersym-

metric generators a

†

b or b

†

a, one may inspect their action on an even–even

nucleus, say

194

Pt, which appears in the example discussed in the next section,

†

194

116

−→ a

† 196

118

−→

195

117

, (3.22)

where bosons and fermions are assumed to have a neutron-hole character.

The supersymmetric generators thus induce a connection between even–even

and odd-mass nuclei with the same total number of bosons plus fermions. A

description with the superalgebra U(6/Ω) leads to a simultaneous treatment

of such pairs of nuclei.

This idea is illustrated schematically in Fig. 3.2 for the case of a partic-

ular U(6/12) supermultiplet. The supermultiplet containing

194

Pt also con-

tains

195

Pt, since the two nuclei are connected by the supersymmetric genera-

tor (3.22). Further action of a

†

b on

195

Pt leads to conﬁgurations whereby two

neutron-holes are coupled to a

198

Pt core, that is, to two-quasiparticle exci-

tations in

196

Pt. This action of a

†

b may continue indeﬁnitely until no more

3.5 A Case Study: Detailed Spectroscopy of

195

Pt 89

Fig. 3.2. Schematic illustration of part of a U(6/12) supermultiplet in the platinum

region. The supermultiplet is characterized by the supersymmetric representation

[N} with N = N + M = 7. A breaking of the U(6/12) supersymmetry leads to a

splitting in the binding energies of the diﬀerent nuclei

bosons are available. A U(6/12) symmetry predicts all states of all nuclei

belonging to the supermultiplet to be degenerate in energy; this degeneracy

is ﬁrst lifted by including U

(6) ⊗ U

(12) invariants which correspond to

nuclear binding energy terms. The analysis then proceeds with the inclu-

sion of Casimir operators of the lower algebras, as schematically indicated

in Fig. 3.2.

3.5 A Case Study: Detailed Spectroscopy of

195

The nucleus

195

Pt is situated in a spherical-to-deformed transitional region.

Its core,

196

Pt, can be reasonably well described as an SO(6) nucleus (see

Sect. 2.2.1). The dominant natural-parity orbits for the neutrons are 3p

1/2

3/2

and 2f

5/2

, which can be decomposed into pseudo-orbital angular mo-

menta

l =0and

l = 2, and pseudo-spin ˜s =1/2. Therefore, the nucleus

195

presents itself as the ideal test of the SO(6) limit of U

(6) ⊗ U

(12) and

U(6/12). The analysis of the empirical evidence for this claim is naturally di-

vided into two parts. In the ﬁrst the validity of the IBFM classiﬁcation (4.16)

195

Pt is studied. In the second part the validity of U(6/12) supersymmetry

for the pair

194

Pt–

195

Pt is analyzed. This section is mainly concerned with

the ﬁrst question and the analysis of supersymmetry in this region is largely

deferred to the discussion of quartet supersymmetry in Sect. 5.4.